Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.194 Medellín nov./dez. 2015
https://doi.org/10.15446/dyna.v82n194.44476
DOI: http://dx.doi.org/10.15446/dyna.v82n194.44476
Comparison of consistency assessment models for isolated horizontal curves in two-lane rural highways
Comparación de modelos de análisis de consistencia para curvas horizontales aisladas en carreteras de dos carriles
Danilo Cárdenas-Aguilar a & Tomás Echaveguren b
a Depatamento de Ingeniería Civil, Facultad de Ingeniería, Universidad de Concepción, Concepción, Chile. ercardenas@udec.cl
b Depatamento de Ingeniería Civil, Facultad de Ingeniería, Universidad de Concepción, Concepción, Chile. techaveg@udec.cl
Received: July 17th, 2014. Received in revised form: May 29th, 2015. Accepted: October 22th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This consistency assessment of highways' geometrical design has the objective of providing safer roads. There are two types of models for consistency assessment: aggregated and disaggregated. The first one considers the difference between design and operating speed at the middle point of isolated horizontal curves. The second one considers the spatial variation of the operating speed profile along the horizontal curve. This paper compares the two types of consistency assessment models, using naturalistic speed and geometry data obtained in 34 horizontal curves of two-lane rural roads in Chile, using a 10 Hz GPS. Results obtained showed that in only 19 cases both methods are equivalent. This equivalence occurred only when operating speed profiles have the lowest spatial variance along the curves. If the operating speed profile has a high variance the consistency level obtained using both methods is different and the better option is combine it.
Keywords: consistency; design speed; operating speed; isolated horizontal curves.
Resumen
El análisis de consistencia del diseño geométrico de carreteras tiene por objetivo contar con carreteras más seguras. Para analizar consistencia existen dos tipos de modelos: agregados y desagregados. Los primeros consideran diferencias de velocidades de diseño y operación en la mitad de la curva. Los segundos consideran la variación espacial del perfil de velocidad de operación. Este trabajo comparó los dos métodos usando datos empíricos de velocidad de operación obtenidos con un GPS de 10 Hz en 34 curvas horizontales simples de carreteras de dos carriles en Chile. Los resultados permitieron concluir que solo en 19 casos los métodos resultaron equivalentes entre sí. Esta compatibilidad sólo se da cuando el perfil de velocidad de operación posee poca varianza especial. Si el perfil de velocidad de operación es muy variable espacialmente, el nivel de consistencia obtenido usando los 2 métodos es diferente, caso en el cual resulta más conveniente combinarlos.
Palabras clave: consistencia; velocidad de diseño; velocidad de operación; curvas horizontales aisladas.
1. Introduction
The consistency of the geometrical design can be defined as the harmony between drivers' expectancy and the geometry of the road. If this harmony is high, drivers can guide their vehicles along the road alignment, minimizing the possibility of making a mistake and having an accident [1]. Consistency assessment provides a tool for highway engineers to discriminate between safer and less safe road designs, and to improve designs, including re-design or to use posted speed signs. There are various consistency assessment models (CAM) that, even though they all seek the same objective, the framework, procedures and indexes are different. A simple taxonomy of CAM makes two classifications: aggregate and disaggregates [2]. The disaggregated CAM allows isolated and "s" shaped horizontal curves to be analyzed and considers the operating speed at the middle point of each curve; the Lamm's model [3] is a good example. Another model is presented in Camacho - Torregrosa et al [4]. The aggregated CAM uses the operating speed profile along road segments to assess the consistency level. The Polus' model falls into this category [5]. Each type of CAM estimates a consistency level of a certain road section, based on consistency indexes. Practical questions include, which model is more suitable for consistency studies, are the models case - dependent, and are the aggregated and disaggregated CAM equivalent? The state of the art does not provide answers to these questions.
The aim of this paper is to compare the Lamm's and Polus' models and to try to seek answers to the above questions. The paper begins with a description of Lamm's and Polus' models, including the algorithms for estimating the consistency index and the consistency levels provided by each one. After the data collection is described, including the road test section selection, the speed and geometry data collection procedure and the data processing are presented. The database used for the study is also included. This is followed by an estimation of the operating and design speed profiles, an estimation of consistency indexes and a description of their comparisons. Finally, a proposal for the integration of a consistency assessment model is presented, based on the findings of this research.
2. Models to be used for consistency assessment
2.1. The Lamm's model
The model postulates that the consistency of isolated horizontal curves is described by using the differences between the operating speed (V85, in km/h) and the design speed (VD, in km/h) at the middle point of the curve. This is shown in eq. (1). The IC is a consistency index (in km/h) for isolated horizontal curves. If the IC value is high, the difference between operating speeds is high, the consistency level is low and the accident risk increases.
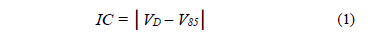
The design speed (VD) can be obtained from project drawings or by back-calculating its value from in-field measurements of the curve geometry. The operating speed (V85) is the 85th percentile of the cumulated frequency distribution of the speed obtained from in-field measurements of instantaneous speed, usually measured at the middle point of the curve. If the operating speed cannot be measured, for instance if there is a new design, it can be obtained by using speed-radius models that are locally calibrated. The Lamm's model grades consistency with the levels "good", "fair" and "poor", using the following thresholds for the IC [6]:
- "good" design: IC ≤ 10 km/h
- "fair" design: 10 km/h < IC ≤ 20 km/h
- "poor" design: IC > 20 km/h
Depending on the consistency level, the road improvements needs can be: do nothing, for "good" designs; limit speed signs, for "fair" or "poor" designs; and redesign, for "poor" designs. Some methods based on consistency levels for estimating speed limits in horizontal curves can be seen in [7,8].
2.2. The Polus' model
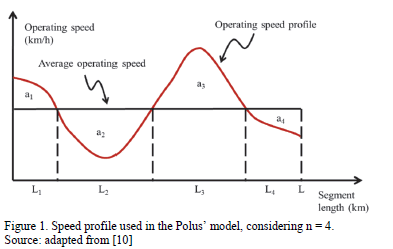
The model estimates the consistency index C of eq. (4), and considers the variability of the operating speed profile around the spatial mean of the operating speed along a road segment [9]. If the variability of the operating speed is high, its variance s (eq. (3), in m/s) is high, the speed parameter Ra (eq. (2), in m/s) is high and the consistency index is low. Lower values of C mean a "poor" consistency level, and higher values mean a "good" consistency level. Therefore, in a consistent design of isolated horizontal curves, a flat speed profile is expected. However, it is not a guarantee that the operating speed will be similar to the design speed.
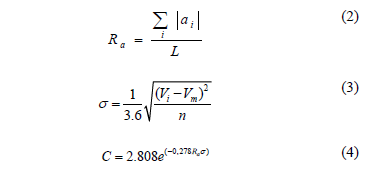
In eq. (2), Ra represents the relative area between the speed profile and the mean speed, normalized by the length of a road section. (See Fig. 1). The term S|ai| is the absolute sum of unitary areas, in m2/s. The term L is the segment length, in m. In eq. (3) the term s represents the standard deviation of the operating speeds, in m/s. Vi is the operating speed at the discrete element of length "i", in km/h. Vm is the spatial average operating speed along the segment of length L and n is the number of discrete elements of length along the segment L, which can be selected arbitrarily. The model rates the consistency level as "good", "fair" and "poor", using the following thresholds for C [9]:
- "good" design: C > 2 m/s
- "fair" design: 1 < C ≤ 2 m/s
- "poor" design: C ≤ 1 m/s
3. Field data collection
3.1. Test sections selection
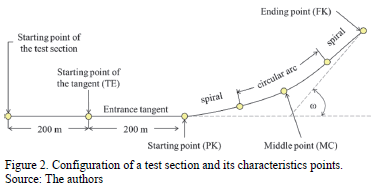
In this research a test section is defined, which is an isolated horizontal curve with a tangent length of up to 400 m in length at the both sides of the curve. It ensures that the horizontal curve is isolated from the neighboring horizontal curves. The selection of test sections was performed in two stages. In the first stage, a preliminary set of test sections was obtained using satellite images, the road network stored in the GIS at the University of Concepcion's Transport Laboratory , the National Road Traffic Survey and the National Road Inventory both Chilean Ministry of Public Works [11-13]. Using this database and the following criteria, 67 test sections were selected.
- Location: only test sections near to Concepcion City were selected in order to reduce the operating costs of taking the measurements.
- Type of pavement surface: only paved surfaces.
- Traffic: annual average daily traffic lower than 5000 vehicles/day-year, according to [14].
- Access: without lateral access or intersections.
- Land use: outside urban areas and without a presence of houses, schools, and farms in the test section or near in order to avoid pedestrian, non-motorized and agricultural machine traffic.
In the second stage, each test section, selected using the previous criteria was inspected in-field. The criteria considered were the following:
- Good pavement condition.
- Test sections without road works.
- Test section with proper lateral clearance and without facilities in lateral areas that could interrupt traffic.
- Test sections in areas in which satellite signal could be destabilized were avoided, such as in areas with dense forest or that have high tension electric towers or electric stations.
- For safety, only test sections with enough clearance for vehicle maneuvers or parking of probe vehicles were selected.
- Test section with low roadside hazard index according to [15].
3.2. Speed and geometry measurements in the test sections
A 10 Hz GPS logger was used for speed measurements. The GPS obtained position data from eight satellites based on RTK (Real Time Kinematics) technology and speed was based on the Doppler Effect, which allows location and speed data to be obtained from a vehicle in motion. The device simultaneously measured position, time, distance, longitudinal speed and heading, as well as other parameters, every 0.1 s, with a precision of 0.2 km/h for speed, 0.05 % for distance and 0.1° for heading [16]. The device uses software for raw-data processing and to generate data reports, with which it is possible to build a speed and position data base. The device can be easily mounted and dis-mounted in a probe vehicle. The device was mounted in the interior part of the windshield of the car and then connected to the GPS antenna. It was placed on the roof and aligned to the longitudinal axis of the vehicle. This position is fixed during the speed measurements.
Speed measurements were obtained using the car following procedure in which the probe vehicle is the follower and the vehicle followed is the leader. The objective is to replicate the speed of the leader vehicle using a probe vehicle (the follower). While this is taking place the probe vehicle tries to keep a constant gap between both vehicles. Details of this measurement procedure can be seen in [17]. The measurement started with the probe vehicle being parked at the roadside with the GPS logger aligned and paused, waiting for a vehicle to enter the test section. Once the vehicle overtakes the probe, the driver turns on the GPS and the probe begins to follow the car and adjusts its speed until the distance between both vehicles is stable, by approximately 50 m. The stabilization of the speed is in the entrance tangent. If the probe vehicle confronts road or traffic conditions that force it to change speed, trajectory or abandon the pursuit, the measurement was discarded. The procedure was repeated between 20 and 30 times per test section, in order to obtain enough speed, position and heading data points.
3.3. Data processing
The data processing allows the horizontal curve geometry and the operating speed to be estimated. The process begins with the coupling and debugging of raw-data by using the Kalman filter implemented in the software of the GPS logger. Data coupling allows the speed-distance and heading-distance signals along the test section to be obtained. The depuration of data consisted in correcting data anomalies or data missing that was caused by dropouts (satellite signal disruption or degradation due to, for instance, the presence of dense forest or high voltage transmission towers). After this distance profiles were built for each run and test section heading: distance and speed -.
4. Geometry and speed profiles estimation
4.1. Geometry estimation
The geometry of the test section was obtained from the heading-distance profile. In these types of diagrams the slope changes allowed the starting and ending point of the curve (PK and FK respectively) to be detected. Once both points are identified, the middle point of the curve (MC) and the starting point (TE) of the entrance tangent were obtained. The TE was located 200 m from the starting point of the curve. After locating the characteristic point, the radius was estimated to be the inverse of the curvature and the curve length to be the distance between the PK and FK points. Fig. 2 shows a generic diagram of the test section.
4.2 Operating speed profile estimation
In each test section the speed-distance diagram of each run were organized in such way that the TE, PK, MC and FK points coincided as much as was possible. Because the trajectory of the probe vehicle is slightly different for each run, an exact coincidence of these points is not possible. Anomalous speed-distance data were erased from the database, and a total of 34 test sections with 20 runs were used in the remainder of the study. The speed-distance profiles were used to estimate operating speed at each characteristic point of the test section. The departure tangent was not considered as drivers usually accelerate and rapidly increase their speed when leaving the horizontal curve, which changes the distance from the probe vehicle. In this case the car pursuit method loses accuracy and does not represent the speed of the leader vehicle. The operating speed was estimated at points TE, PK, MC, and FK as follows. Around each one of these points the 40 neighbor speed data points were grouped (20 data points per side). This procedure was repeated for each run. After the speed data points were grouped, a sample of between 820 and 1230 speed data points was obtained, depending on the number of runs. This sample was used to elaborate an empirical probability density function (pdf). It was fitted to a normal pdf to finally estimate the 85th speed percentile.
4.3. Design speed profile estimation
It was assumed that the design speed is constant along the test section. The design speed was estimated according to the design criterion of the Chilean Highways Manual, which recommends designing horizontal curves, assuming that the superelevation is twice the design friction [18]. Considering this criterion in the mass-point model for horizontal curves design, the design speed (VD in km/h) can be obtained by using eq. (5), in which R is the radius (in m) and f is the design friction coefficient (decimal).
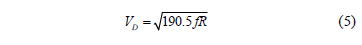
4.4. Summary of data
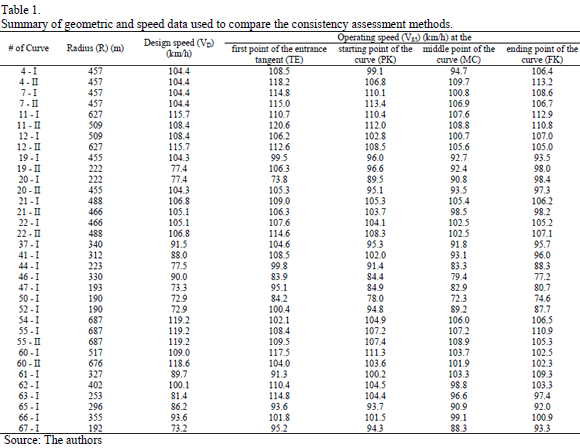
The data obtained for each test section was summarized in an isolated database as is shown Table 1. It includes the geometrical radius, the design speed and the operating speed at each point of the test section.
5. Comparison of Lamm's and Polus' models
5.1. Estimation of the consistency indexes
The consistency indexes were estimated using the data from Table 1. The operating speed at the middle point of the curve (MC) was used to estimate the IC of eq. (1). To estimate the C index of eq. (4) two sceneries were considered. In the first, the value of s (eq. (3)) was obtained using the operating speed and the spatial average value of the operating speed from Table 1. In the second, the mean value of the operating speed was replaced by the design speed in eq. (3), consequently obtaining eq. (6) and eq. (7).
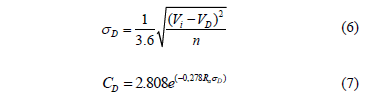
The term Ra of eq. (6) remains the same, but the expression S|ai| is estimated in terms of the operating speed and design speed in each test section. It was assumed that the parameters of the models do not vary if the spatial average speed is replaced by the design speed.
5.2. Comparison of consistency indexes
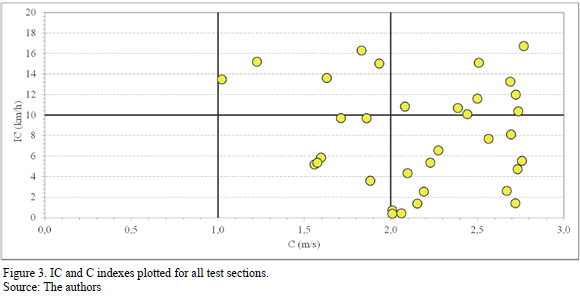
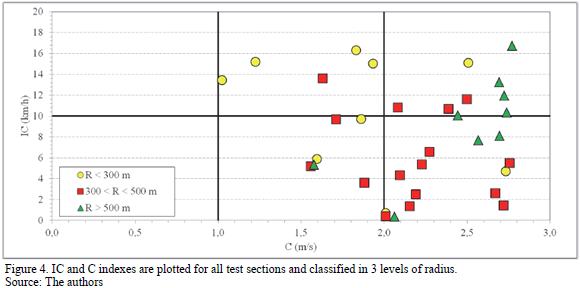
The comparison considered four analyses: (a) comparison between the IC and C indexes for all the test sections (Fig. 3); (b) comparison between the IC and C indexes for all the test sections for 3 levels of radius (Fig. 4); (c) comparison between the IC and C indexes for all test sections, but replacing the spatial average of the operating speed by the design speed (Fig 5); and (d), comparison between the IC and C indexes for 3 levels of radius and replacing the spatial average of the operating speed by the design speed (Fig. 6). In Fig. 3 - 6 the quadrants 1 to 3 represents a "fair" consistency level and the quadrants 4 to 6 represents a "good" consistency level, both according to Lamm's model. Note that for the data analyzed none of the test sections was rated as "poor" according to Lamm's model. Similarly, according to the Polus' model, the quadrants 1 and 4 represent a "poor" consistency level, the quadrants 2 and 5 a "fair" consistency level and the quadrants 3 and 6 a "good" consistency level. Thereby, only in quadrants 2 and 6 are both models of consistency assessment equivalent.
According to Fig. 3, 5 test sections were rated as having a "fair" design and 14 as having a "good" design by the two models (quadrants 2 and 6). However, 15 test sections were rated as having a different consistency level, depending on the method used (quadrants 3 and 5). This ambiguity shows that the actual consistency level cannot be obtained by separately using the CAM.
The test sections located in quadrant 3 of Fig. 3, have differences between the operating and design speeds that are higher than 10 km/h as the operating speed profiles of these curves are approximately uniform along the test sections and the variability of the speed is low. As a consequence, the value of Ra and s are low and, therefore, the C index is high. The consistency level according Polus' model was "good" despite the consistency level according to Lamm's model being described as "fair". This means that if the operating speed profile is uniform, the consistency level will tend to be "good" when using Polus' method, but at the same time it will have a "poor" or "fair" consistency level according to Lamm's method, depending on the differences between the operating and design speeds.
The test sections located in quadrant 5 have a "good" consistency level according to Lamm's model, because the difference between the operating and design speed was lower than 10 km/h. Also, because the operating speed profiles in these test sections were not uniform the values of Ra and s tended to be higher and consequently the C value tends to be low. This behavior is typical of horizontal curves in which the operating speed diminishes at the entrance tangent up to the design speed inside the curve. In this case, Polus' method detected high variability, but Lamm's method only detected harmony between operating and design speed at the middle point of the horizontal curve.
In a second analysis, the comparison of consistency models considered three levels of radius, as shown in Fig. 4. In test sections with a radius lower than 300 m, the consistency level obtained is similar for both models. In test sections with a radius between 300 and 500 m the variability of operating speeds tends to diminish, but the difference between operating speed and design speed do not follow a clear pattern. For this reason, in this segment of radius, the consistency level tends to be "good" when using Polus' model and "good" or "fair" when using Lamm's model. For a radius higher than 500 m, the speed profiles tend to be uniform and the C values tends to be higher. As a consequence, test sections can be located in quadrants 3 or 6 depending on the IC value. The variability of the IC index for higher radius is explained for the operating speed at the entrance tangent. Because the speed profiles are uniforms, if the operating speed at the entrance tangent is very different to the design speed, the CI values increase and the consistency level decrease. Conversely, if the radius is low, the variability of the speed profile increases, especially if the operating speed at the entrance tangent is high. In this case, the C value decreases but the IC value will depend on the difference of that speed with regards to the design speed.
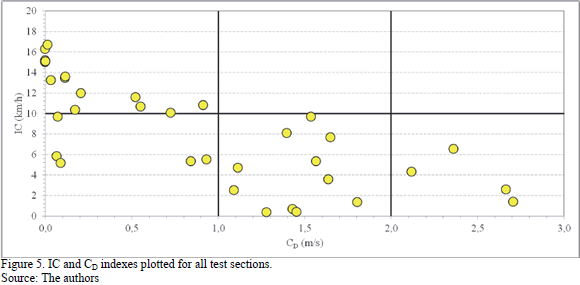
Fig. 5 and 6 show the comparison between the IC index and the modified index of Polus' model (see eq. (7)). Following the same order of the previous analysis, Fig. 5 plots the consistency index for all the test sections and Fig. 6 for three radius levels. The consistency index's observed pattern is different to these observed in Fig. 3 and 4, because both consistency indexes are linked by design speed. In Fig. 5 the test sections that have a low consistency level using the IC index also have a low consistency level using the C index. This means that the test sections exhibit a speed profile that is highly variable that, at the same time, has an operating speed higher than 10 km/h (quadrant 1). Conversely, the test sections that have low IC values, also have higher C values, which means that they have a better consistency level. This is due to the low variability of operating speed profile and the low difference between the operating and design speed.
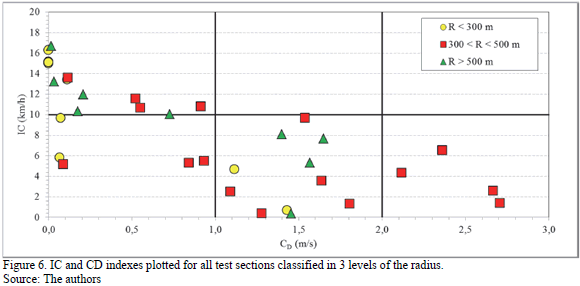
As Fig. 6 shows, this pattern is not only dependent on the radius of the horizontal curves. The pattern is not absolutely clear, but the general trend shows that the test sections with low radii tend to be less consistent than those with higher radii. Test sections with radii lower than 300 m (VD < 85 km/h) simultaneously exhibit high IC values ("fair" design) and low C values ("poor" or "fair" design). This means that the gap between operating and design speed increases at the same time that the operating speed profile oscillates around the design speed. For radii between 300 and 500 m, the pattern is more attenuated. The gap between operating and design speed decreases but not necessarily the variability of the speed profile. However, the oscillation is sufficiently low to increase the consistency level, and according to Polus' model obtains more stable speed profiles.
5.3. Integrated Consistency assessment
From the previous discussion the following aspects can be highlighted:
- The Lam and Polus models are not equivalent but complimentary.
- The lack of equivalence is due to Lamm's model not considering the variability of the speed profile and Polus' model considering the spatial variability of the speed profile with a mean value of operating speed and not with the design speed.
- If complimentary, the consistency level obtained using both models at the same time, depends on the radius, operating speed at the entrance tangent and on the design speed.
- Although that the sample size is not enough to establishes a definitive pattern, when design speed is included in Polus' model, it is observed that both models tend to be correlated. Therefore if the consistency level is "good" according to Lamm's model, it will also be "good" according to Polus' model.
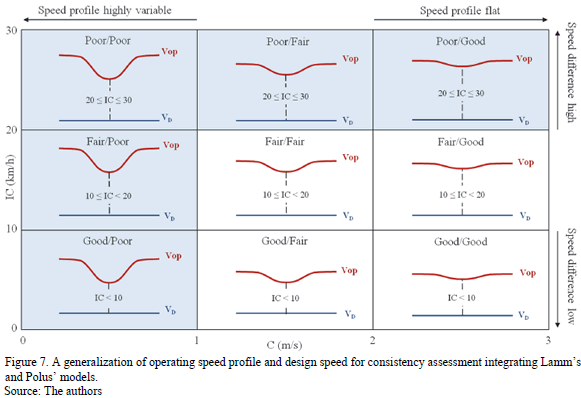
For purposes of geometrical design, the findings of this research are summarized in Fig. 7. This figure shows a generic shape of the speed profile in isolated horizontal curves and the gap between operating speed and design speed, assuming that the operating speed at the entrance tangent is high and that the driver always decelerates when entering the curve. In the figure, Vop represents the operating speed and VD the design speed.
Fig. 7 shows that the better design (the more consistent one) is that in which the operating speed profile is flat and similar to the design speed (quadrant "Good/Good"). The worst design (least consistent) is that in which the operating speed profile is highly variable and the gap between operating speed and design speed is high (quadrant "Poor/Poor"). Other acceptable designs (slightly consistent) are those that obtain speed profiles such as the "Fair/Good", "Fair/Fair" and "Good/Fair" quadrants, in which the operating speed profile is relatively flat and the difference between operating and design speed is lower than 20 km/h. However it is recommended that in these cases the geometrical design included an advisory speed at the entrance tangent to inform drivers about the curve's lack of consistency. Other designs that promote speed profiles associated with the consistency levels "Poor/Poor", "Poor/Fair", "Poor/Good", "Fair/Poor" and "Good/Poor" are not desirable, because lack of consistency increases the risk of accident (The highlighted quadrants in Fig. 7).
6. Conclusions
This paper compared two models for consistency assessment: the Lamm's model, which estimates the consistency level using the difference between the operating and design speed; and the Polus' model, which estimates the consistency level by assessing the spatial variability of the speed profile along a road segment. The comparison was performed for 34 isolated horizontal curves on two-lane rural roads. Speed data, position and headings were obtained using a GPS device.
Lamm's model compares the operating speed with the design speed at the middle point of the curve, and this is not capable of detecting the spatial variability of the operating speed profile. On the other hand, Polus' model detects variability but is not capable of estimating the differences between operating speeds and design speeds. For this reason it was hypothesized that both models are not equivalent but complementary. The results obtained for the 34 horizontal curves studied show evidence of this assumption. Some horizontal curves were rated as "good" using Polus' model because the speed profile was flat, but at the same time were rated as "fair" using Lamm's model because the operating speeds were quite different to the design speed and vice versa.
The study also shows that if the spatial average of the operating speed is replaced by the design speed in Polus' model, coherence with Lamm's model increases. In fact, when the consistency level obtained using Polus' model is high, it is also high under Lamm's model. However, to improve Polus' model using the design speed, a recalibration of the coefficient of the C index could be necessary. As such, this finding should be studied in more detail.
The results obtained with empirical data allow us to propose a general guideline to promote consistent designs of isolated horizontal curves, which was synthetized in a conceptual diagram that included the combination of operating speed profiles and design speed desirables associated to the geometrical design. In general, designs that promote flat operating speed profiles and are similar to designs speed are preferable to ensure that drivers can guide their vehicles along the road in an aligned manner, minimizing the possibility of making a mistake and suffering an accident. This is the essence of consistent geometrical design.
Acknowledgements
The authors thanks to the Chilean National Fund for Scientific and Technological Development (FONDECYT) for supporting the research project FONDECYT 11090029 for which this paper was written.
References
[1] Glennon, J. and Harwood, D., Highway design consistency and systematic design related to highway safety. Transportation Research Record, 682, pp. 77-88, 1978. [ Links ]
[2] Echaveguren, T., Altamira, A., Vargas-Tejeda, S. y Riveros, D., Criterios para el análisis de consistencia del diseño geométrico: Velocidad, fricción, visibilidad y criterios agregados, Proceedings of the Argentinean Conference on Highways and Traffic, pp. 66, 2009. [ Links ]
[3] Lamm, R., Choueiri, E., Hayward, J. and Paluri, A., Possible design procedure to promote design consistency in highway geometric design on two-lane rural roads. Transportation Research Record, 1195, pp. 111-122, 1988. [ Links ]
[4] Camacho-Torregrosa, F., Pérez-Zuriaga, A., Campoy-Ungría, J. and García, A., New geometric design consistency model based on operating speed profiles for road safety evaluation. Accident Analysis & Prevention, 61, pp. 32-42, 2013. DOI: 10.1016/j.aap.2012.10.001 [ Links ]
[5] Polus, A. and Mattar-Habib, C., New consistency model for rural highways and its relationship to safety. Journal of Transportation Engineering, 130(3), pp. 286-293, 2004. DOI: 10.1061/(ASCE)0733-947X(2004)130:3(286) [ Links ]
[6] Lamm, R., Beck, A., Ruscher, T., Mailaneder, T., Cafiso, S. and La Cava, G., How to make two - lane rural roads safer. Boston: Wit Press, 2007. [ Links ]
[7] Echaveguren, T. and Vargas-Tejeda, S., A model for estimating advisory speeds for horizontal curves in two-lane rural roads. Canadian Journal of Civil Engineering, 40, pp. 1234-1243, 2013. DOI: 10.1139/cjce-2012-0549 [ Links ]
[8] Echaveguren, T. and Piña, J., Determinación de límite de velocidad en curvas horizontales de caminos rurales bidireccionales, Proceedings of the Iberoamerican Conference on Road Safety, pp. 79, 2010. [ Links ]
[9] Polus, A., Pollatschek, M. and Mattar-Habib, C., An enhanced integrated design - consistency model for both mountainous highways and its relationship to safety. Road and Transportation Research, 14(4), pp. 13-26, 2005. [ Links ]
[10] Echaveguren, T., Two-lane rural highways consistency analysis using continuous operating speed measurements obtained with GPS. Revista Ingeniería de Construcción, 27(2), pp. 55-70, 2012. DOI: 10.4067/S0718-50732012000200004 [ Links ]
[11] MOP., National highways network. Dimensions and characteristics. Chile: Ministry of Public Works, 2013. [ Links ]
[12] MOP., National traffic survey. Santiago, Chile, Ministry of Public Works, [Online]. 1994 - 2012. [Visited, 10th, may of 2013]. Available at: http://servicios.vialidad.cl/censo/index.htm. [ Links ]
[13] MOP., Proposal of maintenance operations and condition of traveled way and shoulders for paved road network. Chile: Ministry of Public Works, 2012. [ Links ]
[14] Echaveguren, T. and Sáez, J., Estudio de relaciones velocidad - geometría horizontal en vías de la VIII Región, Proceedings of the Congreso Chileno de Ingeniería de Transporte, pp. 341-350, 2001. [ Links ]
[15] Rivera, J.I. and Echaveguren, T., A hazard index for roadside of two-lane rural roads. DYNA, 81(184), pp 55-61, 2014. 10.15446/dyna.v81n184.38929 [ Links ]
[16] Racelogic. VBOX Mini User Guide. United Kingdom: Racelogic, 2008. [ Links ]
[17] Arellano, D., Echaveguren, T. and Vargas-Tejeda, S., A model of truck speed profile in short upwards slopes. Proceedings of the ICE - Transport. 168(5), pp. 466-474, 2015. DOI: 10.1680/tran.13.00012. [ Links ]
[18] MOP. Instrucciones de Diseño. Chile: Ministerio de Obras Públicas, 1994. [ Links ]
D. Cárdenas-Aguilar, is a Civil Engineer from the Universidad Austral de Chile, Chile and obtained his MSc. in 2014 at the Universidad de Concepción, Chile. Since 2012 he has worked for the transport research team at the Universidad de Concepción. His field of research includes road geometrical design, GPS data analysis and road safety. ORCID: 0000-0002-3372-9274
T. Echaveguren, is a Civil Engineer from the Universidad de Concepción and obtained his PhD in 2008 from the Pontificia Universidad Católica, Chile. From 1994 until today he has been a professor at the Universidad de Concepción in Chile. He teaches and researches in the following topics: highways geometric design, road safety and highway asset management, also in association with the Escuela de Ingeniería de Caminos de Montaña (EICAM) at the Universidad Nacional de San Juan, Argentina. He has also advised the Chilean Ministry of Public Works on their low volume road investment plan in Patagonia, and for the last four years has worked on public infrastructure concessions planning. He is currently associate professor in the Civil Engineering Department at the Universidad de Concepción, a member of the Chilean Society of Transportation Engineering, and a member of the Chilean Association of Highways and Transportation, in which is head of the road safety committee. ORCID: 0000-0003-1632-5988