Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.194 Medellín nov./dez. 2015
https://doi.org/10.15446/dyna.v82n194.44297
DOI: http://dx.doi.org/10.15446/dyna.v82n194.44297
Competition between anisotropy and dipolar interaction in multicore nanoparticles: Monte Carlo simulation
Competición entre la anisotropía y la interacción dipolar en nanopartículas multi-núcleo: simulación Monte Carlo
Juanita Londoño-Navarro a, Juan Carlos Riaño-Rojas b & Elisabeth Restrepo-Parra c
a Facultad de Ciencias Exactas y Naturales Universidad Nacional de Colombia, Manizales, Colombia. jlondonon@unal.edu.co
b Facultad de Ciencias Exactas y Naturales Universidad Nacional de Colombia, Manizales, Colombia. jcrianoro@unal.edu.co
c Facultad de Ciencias Exactas y Naturales Universidad Nacional de Colombia, Manizales, Colombia. erestrepopa@unal.edu.co
Received: July 5th, 2014. Received in revised form: March 1rd, 2015. Accepted: October 25th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
Monte Carlo simulations combined with the Heisenberg model and Metropolis algorithm were used to study the equilibrium magnetic properties of magnetic multi-core nanoparticles of magnetite. Three effects were considered in this simulation: the Zeeman effect, magneto crystalline anisotropy, and dipolar interaction. Moreover, the influence of the size distribution (mean diameter and standard deviation) on the magnetization was analyzed. As an important result, a reduction of the equilibrium magnetization caused by the dipolar interaction and the magneto crystalline anisotropy was observed. On the other hand, the nanoparticle size increase produces an enhancement in the equilibrium magnetization, because of the lower influence of dipolar interaction. Cooling temperature effect was also observed, presenting a decrease in the equilibrium magnetization as the temperature was increased. The influence of the easy axis direction was studied.
Keywords: Magnetic multi-core nanoparticle, Monte Carlo, Magnetic dipolar interaction, Magneto crystalline anisotropy
Resumen
Se realizaron simulaciones computacionales empleando Monte Carlo combinado con el modelo de Heisenberg y el algoritmo de Metropolis con el fin de estudiar las propiedades de equilibrio magnético en nano partículas multi-núcleo de magnetita. Se consideraron tres tipos de efectos: Interacción Zeeman, anisotropía magneto cristalina e interacción dipolar. Se observó una reducción en la magnetización debido a la influencia de la interacción dipolar y la anisotropía. Se estudió el efecto de la distribución de tamaños (diámetro medio y desviación estándar) en la magnetización de las nano partículas, obteniéndose un mejor comportamiento magnético para tamaños grandes, ya que, en este caso se reduce la influencia del término de interacción dipolar. Se estudió además el efecto de la temperatura y de la dirección del eje fácil de magnetización sobre las propiedades magnéticas.
Palabras clave: Nanopartículas multi-núcleo, Monte Carlo, Interacción dipolar, Anisotropía magnetocristalina, magnetita.
1. Introduction
Nanostructures have been widely studied for several applications as semiconductors [1], cements [2] mechanics [3] and magnetics [4] among others. The use of magnetic nanoparticles in several technological applications has increased, making the experimental and theoretical investigations very important and even essential [5]. Over the past few years, the scientific community have studied the applications of nanoparticles in medicine and the most important applications have been those using nanoparticles as magnetic carriers in bio separation [6-8], drug delivery [9,10] and mediators for hyperthermia in cancer treatment [11-13]. Magnetic particles composed by several magnetic single domains, named multi-core nanoparticle (MCN), can be used in bio-medical applications [14], because of their higher particle magnetic moment compared to single-core particles containing only one or a few magnetic single domains [15]. The efficiency of the bio-medical applications based on magnetic MCN depends on the well-characterized
magnetic properties of these particles [8,16]. In the case of biomedical application, nanoparticles should be small in order to produce a super-paramagnetic behavior to avoid agglomeration and remain in circulation without being removed by the body's natural filters such as the liver or the immune system [15,17,18]. Magnetic multi-core nanoparticles typically have a hydrodynamic diameter of 50-200 nm containing a magnetic core consisting of a cluster of magnetite (Fe3O4) or magnetite (g-Fe2O3) single domains with a diameter of about 5-20 nm each, surrounded by a non-magnetic coating (e.g. dextranorstarch) [19,20].
There are a few theoretical works in MCN which have studied the magnetic properties of MCN [19,21-22]. Nevertheless, they have not studied the influence of different size distributions of MCN in the magnetic properties of these systems.
In this work, we carried out a numerical investigation in order to study the influence of the single-domain size distribution on the magnetic behavior of MCN systems. Monte Carlo simulation based on the Heisenberg model and Metropolis algorithm were carried out to study the MCN magnetic properties with different single-domain size distribution. The magnetic anisotropy of the single domains and the dipolar interactions between the single domains were considered and their influence on magnetization was studied. The influence of the temperature on magnetization behavior was also studied.
2. Simulations model
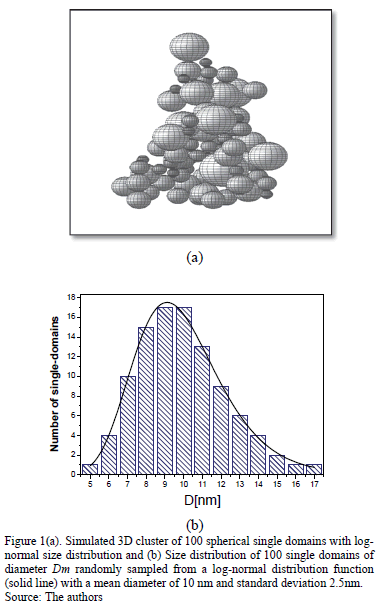
The geometry and model employed in these simulations of MCN are similar to those described by V. Schaller et al. [19]. The geometry consists in a three dimensional cluster of single domains where each domain is randomly located in a finite tree dimensional volume and is in contact with at least one neighbor in the cluster. The sizes of the single domains vary according to a log-normal distribution. Fig. 1(a) shows a cluster of nanoparticles implemented in this work and Fig. 1(b) presents one of the log-normal distributions employed for the simulations. Each single-domain has a uniform magnetization due to the coherent rotation of the atomic moments within the single domain [23]. Hence, the magnetic moment of the single domain is represented by a classical vector with magnitude
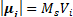 (1)
(1)
where, Ms is the intrinsic saturation magnetization and Vi is the volume of the i-th single domain.
The model is based on a three dimensional classical Heisenberg Hamiltonian which is described by
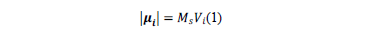
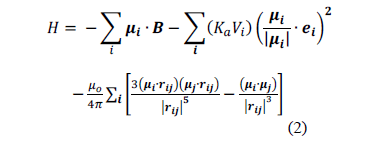
The first term describes the Zeeman energy with 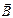 as the external applied magnetic field. The second term corresponds to the anisotropy energy, where
as the external applied magnetic field. The second term corresponds to the anisotropy energy, where 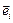 as a unit is the vector along the magnetization easy axis of the single domain, and
as a unit is the vector along the magnetization easy axis of the single domain, and 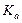 is the anisotropy constant. The last term is the dipolar interaction, where µ0 is the vacuum permeability and
is the anisotropy constant. The last term is the dipolar interaction, where µ0 is the vacuum permeability and 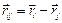 is a distance vector joining the centers of the two dipoles (
is a distance vector joining the centers of the two dipoles (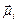 and
and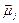 ). This interaction is taken into account if the distance between the single domains is less than or equal to five times the mean diameter. Further increases of the distance do not influence the simulation results for the particle [19].
). This interaction is taken into account if the distance between the single domains is less than or equal to five times the mean diameter. Further increases of the distance do not influence the simulation results for the particle [19].
Monte Carlo simulations with the standard Metropolis algorithm were used for calculating the cluster equilibrium magnetization. A first direction of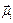 is chosen and H1 is calculated. A random direction of
is chosen and H1 is calculated. A random direction of 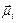 is chosen and H2 is calculated. The difference D;H is calculated and the new direction of
is chosen and H2 is calculated. The difference D;H is calculated and the new direction of 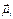 is accepted or rejected according to the Metropolis criterion [24] with the probability determined by the Boltzmann distribution factor exp (-DH/KBT), where KB is the Boltzmann constant and T is the absolute temperature. This procedure is undertaken for all the single domains. Because the MCN is in suspension in a liquid (non-magnetic coating), the rotation of the particle in the liquid must be considered in the algorithm. Then, the interaction energy between the applied magnetic field
is accepted or rejected according to the Metropolis criterion [24] with the probability determined by the Boltzmann distribution factor exp (-DH/KBT), where KB is the Boltzmann constant and T is the absolute temperature. This procedure is undertaken for all the single domains. Because the MCN is in suspension in a liquid (non-magnetic coating), the rotation of the particle in the liquid must be considered in the algorithm. Then, the interaction energy between the applied magnetic field 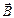 and the total magnetic moment of the particle
and the total magnetic moment of the particle 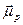 , defined as the vector sum of all the Nth single domains (
, defined as the vector sum of all the Nth single domains (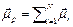 ), is calculated by
), is calculated by

Contrary toV. Schaller et al. [19], we calculated the energy difference D;Hp changing the direction of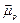 . The direction of
. The direction of 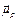 obtained by the sum of all single domains is used to calculate Hp1,Hp2is calculated choosing a random direction of
obtained by the sum of all single domains is used to calculate Hp1,Hp2is calculated choosing a random direction of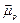 . As explained above the new direction is accepted or rejected according to the metropolis criterion. This procedure is carried out at each Monte Carlo step (MCS).
. As explained above the new direction is accepted or rejected according to the metropolis criterion. This procedure is carried out at each Monte Carlo step (MCS).
The particle equilibrium magnetic properties are characterized by the projection of the particle magnetic moment in the direction of the applied field 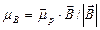 The magnetization is defined as
The magnetization is defined as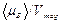 , where
, where 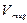 is the sum of the volume of all single domains and
is the sum of the volume of all single domains and 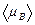 is the average value [19].
is the average value [19].
Around 50000 MCS were considered in order to compute equilibrium averages. The parameter values used in our simulation were an absolute temperature Tof 293K, an intrinsic saturation magnetization of Ms=350kA/m which is a typical value for magnetite single domains in the nanometer range at room temperature. The anisotropy constant used was 1.5x104J/m3; these values were used by Vincent Schaller et al. [19].Three different cases of the easy axis direction were studied: random direction, the magnetic field direction and the single domain direction. All the simulations were carried out for 100 single domains and the sizes varied according to a log-normal distribution. The parameters needed to construct a log-normal distribution are the mean diameter Dm and the standard deviation s of the single domains. In our simulations, we used different size distributions with similar values to those obtained in experimental works of magnetic nanoparticles [19, 2, 5]. These values are shown in Table 1.
3. Results and discussion
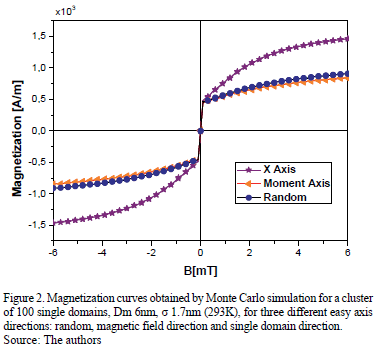
Fig. 2 presents magnetization curves for three different cases of the easy axis direction at a size distribution of Dm=6 nm and s= 3.5 nm. An increase in the magnetization values was observed when the easy axis has the same direction of the external magnetic field. Both, magnetic field and the anisotropy produce an ordering effect in the single domains; therefore, magnetization in this case is higher than in the others. Anisotropy aligned randomly and in the single domain direction can reproduce the real behavior of MCN systems, where the easy axis of each single domain is oriented in different directions.
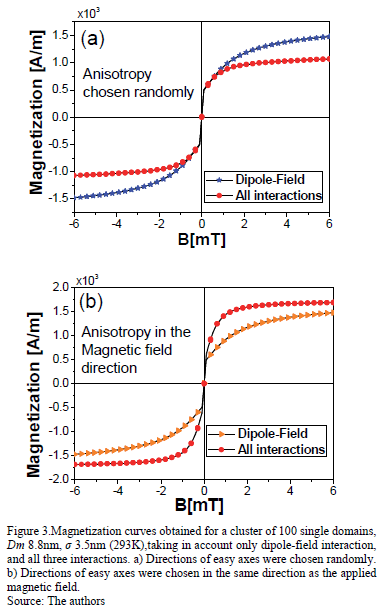
Figs. 3(a) and 3(b) show the influence of the anisotropy and the dipolar interaction on the magnetization depending on the applied field. Curves at room temperature (293K) for two cases of easy axis direction were obtained: at random and the external magnetic field directions.
Parameters used were Dm=8.8nm and a standard deviation s=3.5nm; the external magnetic field direction remained constant in the x-axis. Fig. 3(a) shows the magnetic curves when the direction of the easy axis was randomly chosen. The signature of both, dipolar interaction and anisotropy effects on these systems is a reduction of equilibrium magnetization [19,22]. According to the reports [26], it must be stressed that the resulting magnetic structure depends upon the anisotropy and consequently magnetization is affected. Fig. 3(b) shows the magnetic curves when the easy axis was chosen in the magnetic field direction. In this case, the magnetic behavior is contrary to the random case, it is because the anisotropy generates an ordering in the system, and it aligns the single domains. This effect combined with the alignment generated by the magnetic field produces a higher magnetization. According to the literature, for the case of a nonzero anisotropy (KV≠ 0), the magnitude of the average value of atomic spin projection onto the rotating total moment direction depends on the angle between the anisotropy axis and the direction of the total magnetic moment [27]. Regarding the dipolar interaction effect, it seems to have a poor influence on the magnetic properties. This interaction enlarges the disorder of the magnetic moments but not as simply as thermal fluctuations do. Firstly, the structure of the systems-spatial arrangement and easy axis distribution-affects the energy barrier distribution and consequently affects the magnetization process; secondly, the dipolar interaction can also introduce a certain magnetic order which also gives rise to a large spread in the effective energy barrier distribution as the nanoparticles concentration increases [28].
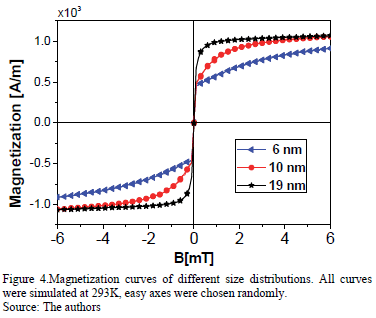
In Fig. 4, the magnetization obtained for different size distribution is plotted as a function of the applied magnetic field. Random directions of easy axes were chosen to simulate real cases. These curve shows that the saturation magnetization decreases as the sizes of the single domains decrease. This behavior has been reported for magnetic nanoparticles in experimental works [29-31]; nevertheless it is attributed to a surface disorder in small nanoparticles due to the increased surface/volume ratio [30,32].
F. Tournus et al. [33] stated that the final moment of a nanoparticle assembly is proportional to its volume. In this work, we have represented MCN as a system composed by spherical particles with uniform magnetization, according to the Stoner and Wohlfarth model [32,34]. It means that all spins are collinear and rotate coherently without differentiating the core and surface nanoparticle components. This representation is valid for small particles and dense systems [32], hence the obtained results indicate that the reduction in the saturation magnetization is not only associated to surface disorder but also to the sizes of the single domains (MCN size). Thus, this could be due to dipolar interactions being dominant among small sized nanoparticles due to less separation between the magnetic particles. According to many experiments, substantial dipolar interactions between nanoparticles in a compacted sample (as presented here) were observed, finding evidence that the nanoparticles in dense samples are organized in a dipolar super spin-glass system [35]. Then, the super paramagnetic behavior is better observed in small particles (6nm and10nm), and when the particle size increases, the magnetic behavior tends to be ferromagnetic. The magnetite particles are ferromagnetic when they exceed the super paramagnetic limit, which is in the order of 26nm at room temperature [35]. Thus, it could be concluded that for different applications (i.e. medical interest), the nanoparticles size is highly relevant. If the nanoparticle size is lower than a critical value, the dipolar interaction increases, this being negative for the total magnetization (that decreases). On the other hand, if nanoparticle size is greater than the critical value, not only do the nanoparticle clusters tend to behave in a ferromagnetic way, but they are also difficult to transport into the body and to eliminate.
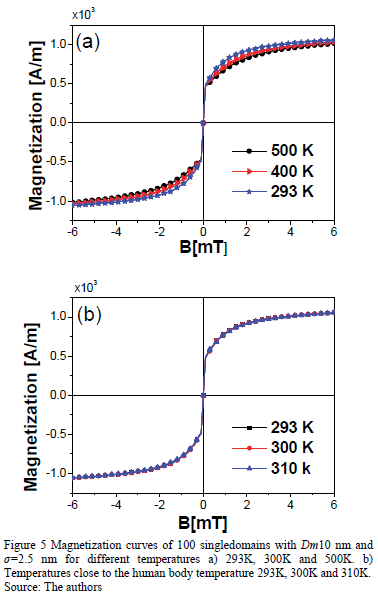
Figs. 5(a) and 5(b) show the magnetization as a function of the applied magnetic field of 100 single domains with Dm10nm and s of 2.5 nm for different temperatures. Easy axes were chosen randomly. The obtained behavior in Fig. 5(a) is consistent with the expected; as the temperature increases, the magnetization exhibits a slight increment. The small reduction in the magnetization is due to the small disorder caused by the temperature in the orientation of the single-domain magnetic moments that presents a competition with the magnetic field. Given that one of the most important applications of these nanoparticles is in medicine-as they are inserted into biological organisms-Fig. 5(b) shows the magnetization curve for temperatures close to the human body temperature. This behavior allows us to observe that the multicore nanoparticles exhibit a super paramagnetic behavior presenting almost the same magnetization, this being a suitable characteristic for medical applications in the human body.
4. Conclusions
The magnetic properties of MCN were studied using Monte Carlo simulations combined with the Metropolis Algorithm. In agreement with previous works, a reduction in the equilibrium magnetization was observed as a consequence of dipolar interaction and anisotropy The magnetization behaviour of different size distributions was studied, observing that the reduction in size of the nanoparticles produces a decrease in the saturation magnetization, caused by the increase in the dipolar interaction. The influence of the temperature on the magnetization was also studied, finding that temperature generates a disorder in the system causing a reduction in the magnetization. It was also found that for temperatures close to the human body temperature, the magnetic behaviour of MCN does not change.
The influence of the easy axis direction in the magnetization behaviour was studied, and it was found that the random direction decreases the magnetic behaviour generating a disorder in the system. The magnetization increased when the easy axis was chosen in the same direction as the applied magnetic field; in this case, the anisotropy increased the magnetic ordering in the system, in contrast to the random case.
Acknowledgments
The authors gratefully acknowledge the financial support of the Dirección Nacional de Investigaciones at Universidad Nacional de Colombia during the course of this research, under project 12920 "Desarrollo teórico-experimental de nanoestructuras basadas en Bismuto y materiales similares" approved by the Convocatoria Nacional de Investigación I Creación Artística de la Universidad Nacional de Colombia 2010-2012
References
[1] Raba-Paez, A.M., Suárez, D.N., Martínez, J.J., Rojas-Sarmiento, H.A. and Rincón-Joya, M., Pechini method used in the obtention of semiconductor nanoparticles based niobium, DYNA, 82(189), pp. 52-58, 2015. DOI: 10.15446/dyna.v82n189.42036 [ Links ]
[2] Tobón, J.I, Restrepo-Baena, O.J. y Payá-Bernabeu, J.J., Adición de nanopartículas al cemento Portland, DYNA, 74(152), pp. 277-291, 2007. [ Links ]
[3] Gallego, J., Sierra-Gallego, G., Daza, C., Molina, R., Barrault, J., Batiot-Dupeyat, C. and Mondragón, F., Production of carbon nanotubes and hydrogen by catalytic ethanol decomposition, DYNA, 80(178), pp. 78-85, 2013. [ Links ]
[4] Jiménez-Pérez, J.L., Sánchez-Ramírez, J.F., Correa-Pacheco, Z.N., Cruz-Orea, A., Chigo-Anota, E. and Sánchez-Sinencio, F., Thermal characterization of solutions containing gold nanoparticles at different pH values. Int J Thermophys, 34, pp. 955-961, 2013. DOI: 10.1007/s10765-012-1372-0 [ Links ]
[5] Lan, T.N. and Hai, T.H., Monte Carlo simulation of magnetic nanoparticle systems, Computational Materials Science, 49, pp. S287-S290, 2010. DOI: 10.1016/j.commatsci.2010.01.025 [ Links ]
[6] Sieben, S., Bergemann, C., Lübbe, A., Brockmann, B. and Rescheleit D., Comparison of different particles and methods for magnetic isolation of circulating tumor cells, Journal of Magnetism and Magnetic Materials, 225, pp. 175-179, 2001. DOI: 10.1016/S0304-8853(00)01248-8 [ Links ]
[7] Adolphi, N.L., Huber, D.L., Jaetao, J.E., Bryant, H.C., Lovato, D.M., Fegan, D.L., Venturini, E.L., Monson, T.C. and Tessier, T.E., Hathaway, H. J., Bergemann, C., Larson, R. S. and Flynn E. R. Characterization of magnetite nanoparticles for SQUID-relaxometry and Magnetic Needle Biopsy, Journal of Magnetism and Magnetic Materials, 321, pp. 1459-1464, 2009. DOI: 10.1016/j.jmmm.2009.02.067 [ Links ]
[8] Schaller, V., Kräling, U., Rusu, C., Petersson, K., Wipenmyr, J., Krozer, A., Wahnström, G., Sanz-Velasco, A., Enoksson, P. and Johansson, C. Motion of nanometre sized magnetic particles in a magnetic field gradient, Journal of Applied Physic,. 104, pp. 093918-093932, 2008. DOI: 10.1063/1.3009686 [ Links ]
[9] Steinfeld, U., Pauli, C., Kaltz, N., Bergemann, C. and Lee, H.H., T lymphocytes as potential therapeutic drug carrier for cancer treatment, International Journal of Pharmaceutics, 311, pp. 229-236, 2006. DOI: 10.1016/j.ijpharm.2005.12.040 [ Links ]
[10] Yang, J., Lee, C.H., Park, J., Seo, S., Lim, E.K., Song, Y.J., Suh, J.S., Yoon, H.G., Huh, Y.M. and Haam S., Antibody conjugated magnetic PLGA nanoparticles for diagnosis and treatment of breast cancer, Journal of Materials Chemistry, 17, pp. 2695-2699, 2007. DOI: 10.1039/B702538F [ Links ]
[11] Kettering, M., Winter, J., Zeisberger, M., Bremer-Streck, S., Oehring, H., Bergemann, C., Alexiou, C., Hergt, R. and Halbhuber, K., Magnetic nanoparticles as bimodal tools in magnetically induced labelling and magnetic heating of tumor cells: An in vitro study, Nanotechnology, 18, pp. 175101, 2007. DOI: 10.1088/0957-4484/18/17/175101 [ Links ]
[12] Dutz, S., Clement, J.H., Eberbeck, D., Gelbrich, T., Hergt, R., Muller, R., Wotschadio, J. and Zeisberger M., Ferrofluids of magnetic multicore nanoparticles for biomedical applications, Journal of Magnetism and Magnetic Materials, 321, pp. 1501-1504, 2009. DOI: 10.1016/j.jmmm.2009.02.073 [ Links ]
[13] Kallumadil, M., Tada, M., Nakagawa, T., Abe, M., Southern, P. and Pankhurst, Q.A., Suitability of commercial colloids for magnetic hyperthermia, Journal of Magnetism and Magnetic Materials, 321, pp. 1509-1513, 2009. DOI: 10.1016/j.jmmm.2009.02.075 [ Links ]
[14] Dutz, S., Kettering, M., Hilger, I., Müller, R., and Zeisberger, M., Magnetic multicore nanoparticles for hyperthermia -influence of particle immobilisation in tumour tissue on magnetic properties, Nanotechnology, 22, pp. 265102, 2011. DOI: 10.1088/0957-4484/22/26/265102 [ Links ]
[15] Pankhurst, Q.A., Connoly, J., Jones, S.K. and Dobson, J., Applications of magnetic nanoparticles in biomedicine, Journal of Physics D: Applied Physics, 36, pp. R167-R181, 2003. DOI: 10.1007/978-0-387-85600-1_20 [ Links ]
[16] Astalan, A.P., Johansson, C., Petersson, K., Blomgren, J., Ilver, D., Krozer, A. and Johansson, A., Magnetic response of thermally blocked nanoparticles in a pulsed magnetic field, Journal of Magnetism and Magnetic Materials, 311, pp. 166-170, 2007. DOI: 10.1016/j.jmmm.2006.10.1182 [ Links ]
[17] Chomoucka, J., Drbohlavova, J., Huska, D., Adam, V., Kizek, R. and Hubalek, J. Magnetic nanoparticles and targeted drug delivering, Pharmacological Research, 62, pp. 144-149, 2010. DOI: 10.1016/j.phrs.2010.01.014 [ Links ]
[18] Balakrishnan, S., Bonder, M.J. and Hadjipanayis, G.C., Particle size effect on phase and magnetic properties of polymer-coated magnetic nanoparticles, Journal of Magnetism and Magnetic Materials, 321, pp. 117-122, 2009. DOI: 10.1016/j.jmmm.2008.08.055 [ Links ]
[19] Schaller, V., Wahnström, G., Sanz-Velasco, A., Enoksson, P. and Johansson, C., Monte Carlo simulation of magnetic multi-core nanoparticles, Journal of Magnetism and Magnetic Materials, 321, pp. 1400-1403, 2009. DOI: 10.1016/j.jmmm.2009.02.047 [ Links ]
[20] Tartaj, P., del-Puerto-Morales, M., Veintemillas-Verdaguer S., Gonzales-Carreño, T. and Serna C.J., The preparation of magnetic nanoparticles for applications in biomedicine, Journal of Physics D: Applied Physics, 36, pp. R182-R197, 2003. [ Links ]
[21] Weddemann, A., Auge, A., Kappe, D., Wittbracht, F. and Hütten A., Dynamic simulations of the dipolar driven demagnetization process of magnetic multi-core nanoparticles, Journal of Magnetism and Magnetic Materials, 322, pp. 643-646, 2010. DOI: 10.1016/j.jmmm.2009.10.031 [ Links ]
[22] Schaller, V., Wahnström. G., Sanz-Velasco, A., Gustafsson, S., Olsson, E., Enoksson, P. and Johansson, C., Effective magnetic moment of magnetic multicore nanoparticles, Physical Review B, 80, pp. 092406, 2009. DOI: 10.1103/PhysRevB.80.092406 [ Links ]
[23] Bean, C.P. and Livingston, J.D., Superparamagntism, Journal of Applied Physics, 30, pp. 120S-129S, 1959. DOI: 10.1063/1.2185850 [ Links ]
[24] Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H. and Teller, E., Equation of state calculations by fast computing machines, Journal of Chemical physics, 21, pp. 1087-1092, 1953. DOI: 10.1063/1.1699114 [ Links ]
[25] Balakrishnan, S., Bonder, M.J. and Hadjipanayis G.C., Particle size effect on phase and magnetic properties of polymer-coated magnetic nanoparticles, Journal of Magnetism and Magnetic Materials, 321, pp. 117-122, 2009. DOI: 10.1016/j.jmmm.2008.08.055 [ Links ]
[26] Mazo-Zuluaga, J., Restrepo, J. and Mejía-López, J., Surface anisotropy of a Fe3O4 nanoparticle: A simulation approach, Physica B, 398, pp. 187-190, 2007. DOI: 10.1016/j.physb.2007.04.070 [ Links ]
[27] Kokorina, E.E. and Medvedev, M.V., Magnetization curves of nanoparticle with single-ion uniaxial anisotropy, Journal of Magnetism and Magnetic Materials, 310, pp. 2364-2366, 2007. DOI: 10.1016/j.jmmm.2006.11.107 [ Links ]
[28] Mao, Z., Chen, D. and He Z., Equilibrium magnetic properties of dipolar interacting ferromagnetic nanoparticles, Journal of Magnetism and Magnetic Materials, 320, pp. 2335-2338, 2008. DOI: 10.1016/j.jmmm.2008.04.118 [ Links ]
[29] Nishio, K., Ikeda, M., Gokon, N., Tsubouchi, S., Narimatsu, H., Mochizuki, Y., Sakamoto, S., Sandhu, A., Abe, M. and Handa, H., Preparation of size-controlled (30-100 nm) magnetite nanoparticles for biomedical applications, Journal of Magnetism and Magnetic Materials, 310, pp. 2408-2410, 2007. DOI: 10.1016/j.jmmm.2006.10.795 [ Links ]
[30] Gonzalez-Fernandez, M.A., Torres, T.E., Andrés-Vergés, M., Costo, R., de-la-Presa, P., Serna, C.J., Morales, M.P., Marquina, C., Ibarra, M.R. and Goya, G.F., Magnetic nanoparticles for power absorption: Optimizing size, shape and magnetic properties, Journal of Solid State Chemestry, 182, pp. 2779-2784, 2009. DOI: 10.1016/j.jssc.2009.07.047 [ Links ]
[31] Salado, J., Insausti, M., Gil-de-Muro, I., Lezama, L. and Rojo, T., Synthesis and magnetic properties of monodisperse Fe3O4 nanoparticles with controlled sizes, Journal of Non-Crystalline Solids, 354, pp. 5207-5209, 2008. DOI: 10.1016/j.jnoncrysol.2008.05.063 [ Links ]
[32] Papaefthymiou G.C., Nanoparticle magnetism, Nano Today, 4, pp. 438-447, 2009. DOI: 10.1016/j.nantod.2009.08.006 [ Links ]
[33] Tournus, F. and Tamion, A., Magnetic susceptibility curves of a nanoparticle assembly II. Simulation and analysis of ZFC/FC curves in the case of a magnetic anisotropy energy distribution, Journal of Magnetism and Magnetic Materials, 323, pp. 1118-1127, 2011. DOI: 10.1016/j.jmmm.2010.11.057 [ Links ]
[34] Petracic, O., Superparamagnetic nanoparticle ensembles, Superlattices and Microstructures, 47, pp. 569-578, 2010. DOI: 10.1016/j.spmi.2010.01.009 [ Links ]
[35] Nadeem, K., Krenn, H., Traussnig, T., Würschum, R., Szabo, D.V. and Letofsky-Papst, I., Effect of dipolar and exchange interactions on magnetic blocking of maghemite nanoparticles, Journal of Magnetism and Magnetic Materials, 323, pp. 1998-2004, 2011. DOI: 10.1016/j.jmmm.2011.02.041 [ Links ]
E. Restrepo-Parra, completed her BSc. Eng in Electrical Engineering in 1990 at the Universidad Tecnológica de Pereira, her MSc. degree in Physics in 2000, and PhD. degree in Automation Engineering in 2009, both at Universidad Nacional de Colombia, Manizales, Colombia. From 1991 to 1995, she worked in the Colombian electrical sector and since 1996 for the Universidad Nacional de Colombia. Currently, she is a senior Professor in the Physics and Chemistry Department, Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Colombia - Sede Manizales. Her research interests include: simulation and modeling of materials properties by several methods; Materials processing by plasma assisted technique and materials characterization. She is currently the director of the Laboratories at the Manizales campus of Universidad Nacional de Colombia. ORCID 0000-0002-1734-1173
J. Riaño-Rojas, completed his BSc. in Mathematics in 1993, his MSc degree in Mathematics in 1998 and his PhD. in Automation Engineering in 2010 at Universidad Nacional de Colombia. Currently, he is a full professor in the Mathematics and Statistics Department, Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Colombia, Manizales, Colombia. His research interests include: simulation and modeling of materials properties by several methods, among others. He is currently the director of PCM Computational Applications research group at Universidad Nacional de Colombia. ORCID 0000-0002-5719-2854
J. Londoño-Navarro, completed hers BSc. Eng. in Physical Engineering in 2011 at Universidad Nacional de Colombia, Manizales, Colombia. She is currently finishing a MSc degree in Physics at the same university. Her research interests include: simulation and modeling of materials properties by several methods, among others. ORCID 0000-0001-6165-0160