DOI: http://dx.doi.org/10.15446/dyna.v82n194.46333

Experimental behavior of a masonry wall supported on a RC two-way slab

Comportamiento experimental de un muro de mampostería apoyado sobre una losa de concreto reforzado

 

Alonso Gómez-Bernal ^a, Daniel A. Manzanares-Ponce ^b, Omar Vargas-Arguello ^c, Eduardo Arellano-Méndez ^d, Hugón Juárez-García ^e, & Oscar M. González-Cuevas ^f

 

^a Departamento de Materiales, Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México. agb@correo.azc.uam.mx
^b Posgrado Ing. Estructural División de CBI, Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México. dmanzanares@anivip.org.mx
^c Posgrado Ing. Estructural División de CBI, Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México. omanem_9@hotmail.com
^d Departamento de Materiales, Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México. eam@correo.azc.uam.mx
^e Departamento de Materiales, Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México. hjg@correo.azc.uam.mx
^f Departamento de Materiales, Universidad Autónoma Metropolitana Azcapotzalco, México, D.F., México. omgc@correo.azc.uam.mx

 

Received: October 17^th, 2014. Received in revised form: March 29^th, 2015. Accepted: October 22^th, 2015

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
This paper discusses the experimental results of a prototype slab-wall that is subjected to vertical and horizontal cyclic loading. The key aspects under discussion are: (a) the differences between the capacity resistance of a wall supported on a slab vs. a wall supported on a fixed base, (b) the implications when shear walls are placed directly on transfer concrete slabs, and (c) the effects that these walls cause on the slabs. The most important results presented herein are the change on lateral stiffness and resistance capacity of the load-bearing wall supported on a slab versus the wall supported on a fixed base. Analytical finite element slab-wall models were built using ANSYS. During the experimental test process of horizontal loading, we detected that the stiffness of the slab-wall system decreased by a third compared to the one on the fixed base wall; a result that supported by the numerical models.

Keywords: transfer slab; masonry wall test; concrete slab test; finite element.

Resumen
Este trabajo analiza los resultados experimentales de un prototipo losa-muro sometido a cargas verticales y horizontales cíclicas. Los aspectos claves en estudio son: (a) las diferencias entre la capacidad resistente de un muro apoyado sobre una losa contra la de otro apoyado sobre base rígida, (b) las implicaciones cuando un muro de carga se desplanta sobre losas de transferencia y (c) los efectos que causan estos muros en las losas de concreto reforzado. Los resultados más importantes encontrados son las diferencias de rigidez lateral y de capacidad resistente del muro apoyada sobre la losa, respecto al empotrado en su base. Para apoyar los resultados del estudio, varios modelos de elementos finitos losa-muro fueron estudiados usando ANSYS. Durante el proceso de prueba con carga horizontal, se detectó que la rigidez de la losa-muro del sistema disminuye a la tercera parte, respecto de la pared fija, este resultado es apoyado por el estudio numérico.

Palabras clave: losas de transferencia; ensaye de muros; muros de mampostería; ensaye losas de concreto; elemento finito.

---

 

1. Introduction

In Mexican cities the construction of medium-rise buildings with a structural floor system called "transfer slabs" have been popularized over recent years. Researchers [1] evaluated a set of new buildings constructed in a sector of Mexico City called Colonia Roma, which was severely damaged during the 1985 earthquake. They detected a high percentage of buildings that were designed with discontinuous walls, a structural configuration that induced soft story in some buildings. Furthermore, many of them are projected with transfer floor systems. This situation is worrying because it is known that buildings with discontinuity in elevation are vulnerable to seismic loads. This situation is critical when load-bearing walls, especially on the first floor, are not aligned with the vertical forces, therefore increasing seismic vulnerability increased.

These structures have a floor system (transfer slab or transfer floor) supported on one rigid level, which is used as a parking lot. On top of this transfer slab, a four-story shear wall super-structure is constructed. A large percentage of these walls are interrupted at the transfer floor level, and they are not continuous through the foundation. However, a few walls are continuous in height over the edges of the structure, but a significant percentage of walls in the upper stories are not aligned with the axes of the frames of the first floor. This structural configuration causes a significant increase in the shear stress in these walls, as is observed and discussed in detail in the following references [2,3]. This can be explained due to the excessive deflections that walls induce to the slab. The shear forces calculated are two to three times larger than those that these walls would have if they were continuous throughout all their height. In addition, the transfer slab is exposed to additional stresses and high deformations.

The transfer floor system requires further investigation, and in this work the fundamental objective is to analyze, using an experimental model, the interaction between the wall and the slab on which is supported. There are significant differences in behavior between these systems and the traditional ones that do not have discontinuities. Several slab-wall numerical models were also analyzed using ANSYS in order to characterize the behavior of a transfer slab system. In the experimental phase a full-scale slab-wall specimen was designed, built and tested by cyclic loads in the Laboratory of Structures at UAM-Azcapotzalco. The prototype slab-wall was subjected to three load patterns: 1) gravitational load; 2) horizontal load only; and 3) a combination of gravitational and lateral loads.

Mexico and other countries have conducted experimental research on the behavior of load-bearing walls subjected to lateral forces in order to characterize the seismic effects. Walls that have different characteristics, in terms of materials, reinforcement, load conditions and other properties have been tested [4-7], and some of the most notable results were documented [8]. Moreover, in terms of the experimental behavior of concrete slabs, there is less information due to the limited number of tests performed [9,10]. In the limited research the slabs were subjected to distributed or concentrated loads; however, there was no specific linear loads information directly applied on the slabs (walls supported on the slabs).

 

2. Experimental model

The experimental test included three load protocols: (1) gravitational loads with less than 8 Tons, which is the vertical loading observed in buildings that have the stated floor system, (2) horizontal cyclic loads with a relatively low value that are used in order to study the linear response, and (3) gravitational constant loads with less than 8 Tons that are combined with horizontal increased loading cycles until the failure of the system is reached.

2.1 Geometry and reinforcement

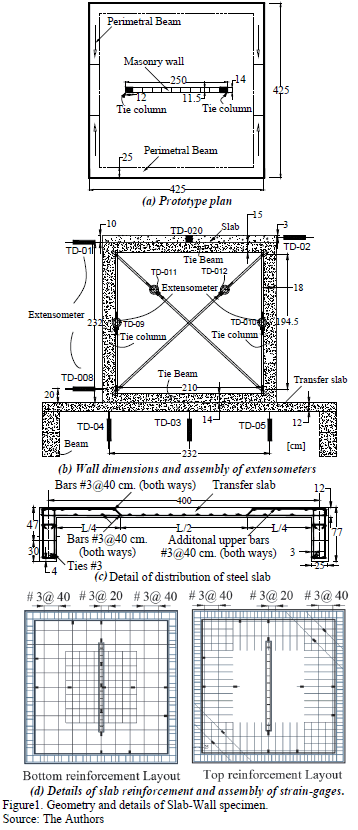
The specimen consists of a masonry wall placed on top of a squared two-way slab of 4.25 m in width, and 12 cm thick, with four reinforced concrete beams (25 x 77) cm along the perimeter. The slab and beams were monolithically casted. The concrete strength was f'_c=250 kg/cm². The details and steel reinforcement in the slab were designed using conventional procedures, such as the ones used in real buildings in Mexico City. On the outer strips, the spacing of the bottom re-bars was set to 40 cm. On the central strip, the spacing was set to 20 cm in both directions. In the top of the slab, the reinforcement spacing was also set to 20 cm. Fig. 1 shows details of the reinforcement used in the slab specimen.

The masonry wall that is 2.50 m wide by 2.41m high, was placed on the slab's central strip. The wall is confined with two tie-columns, 14 cm x 18 cm, and with a tie-beam, 14 cm x 14 cm. The bottom tie-beam was integrated with the slab. The concrete resistance of the tie-columns was f'_c=150 kg/cm², with four re-bars in the corners. The re-bars complied with the minimum steel requirements of the Mexico City code for masonry structures [11].

2.2. Setup, devices, and instrumentation

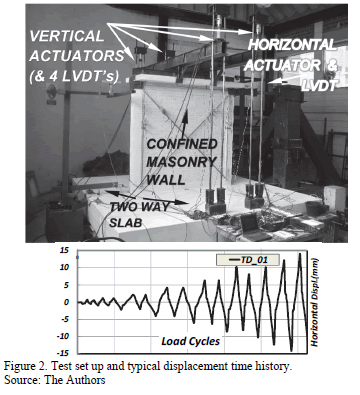
We designed and built three mechanical steel devices that helped with the experimental protocol of the specimen: one for attachment purposes, the second one for using in vertical loading, and the third one for horizontal loading. The attachment device prevented the slab-wall specimen from moving in a horizontal or vertical way during the test whenever the loads were applied to the wall. This anchor system consists of a set of steel girders that are fixed in the Laboratory's reaction slab. The gravitational load device was constituted by a system of steel beams, eight tensors and their anchorages (see Fig. 2). The main girders have a box section that is made out of two I sections welded together by its flanges, and reinforced with stiffeners. At the top of the girders there are four vertical actuators (each with a 25 ton capacity), supported on a base plate, which keeps them in an upright position and prevents them from slippage. At the ends, there are re-bars that connect down to the perimeter reinforced concrete beams. The third device was designed for the incremental cyclic horizontal loading. We used a double-action hydraulic actuator with a 25 ton push capacity, and a 12 ton pull capacity. We estimated that the lateral capacity of the wall would reach 12 tons. The corresponding LVDT's were attached to each actuator (four verticals and one horizontal).

The measurement of the strains in the model was possible due to a set of strain gages (SGs) that were installed in the reinforcement of the concrete elements. The slabs had 16 SGs in the bottom and 16 SGs in the top of the slab. The tie-columns of the masonry wall had 20 SGs in the longitudinal re-bars. And finally, there were 10 SGs in the concrete slab and the tie-columns [12]. In order to record the displacements of the slab and the wall, twenty extensometers (TD) were also installed at strategic points, Fig. 1.

 

3. Numerical models

In the literature, several experimental and theoretical research studies assumed that shear walls are supported on a non-deformable base. In this research, we considered that the walls are supported on a flexible base, and that the performance of the wall-slab system might be different to the one observed for rigid base supports. Our interest is in the definition of the deformation relationship of the wall-slab system; for example, the determination of the relationship between the slab deformation and the wall crack pattern will define the serviceability conditions for these types of structures. These results are important because they will clarify the reasons for the occurrence of a particular crack pattern on the first story walls in buildings with transfer-slabs.

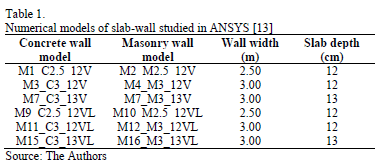
Detailed numerical non-linear models for the slab-wall system were analyzed [13] using ANSYS software [14]. Several geometries were studied, and two materials were used for the wall: masonry and reinforced concrete. Table 1 shows the geometric characteristics of six studied models: four wall lengths and two slab thicknesses. The model was divided in two sections for reducing computational time in analysis. The support conditions of the slab is supposedly restricted on all edges. The M10_M2.5_12V and M10_M2.5_12VL models are similar to the tested specimen.

One of the main goals was the definition of capacity curves for the slab-wall models subjected firstly to incremental vertical loading and secondly to a constant gravitational load combined with incremental cyclic horizontal loading. In the vertical loading models group an additional model subjected to uniform loading without any wall was included for the purposes of comparison. For the lateral loading group, a non-linear model with wall on a rigid base was used for the purposes of comparison (wall on flexible base).

 

4. Definition of specimen response

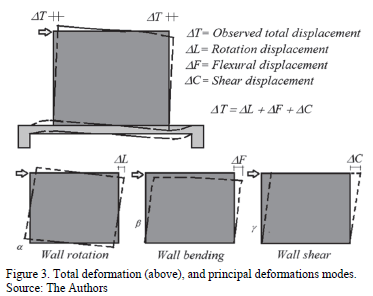
Different configurations, or deformation modes, of the slab-wall model in each of the three loading protocols (vertical, horizontal, and combined), define the structural behavior and the failure of the system (Fig. 2). Thus, the failure in the tested wall will depend on the bending (DF) and shear (DC) deformations induced by lateral loading. However, in this case, since the wall is supported by a slab, the lateral displacement due to the wall rotation (DL), induced by the slab deformation, has to be considered. Total displacement at the top of the wall DT is then induced and presented in Fig. 3.

Shear deformations in the wall can be obtained from the records of displacement transducers that are installed in diagonal directions. Based on the strength of materials theory, the unitary angular deformation, g, is due to the shear stress acting on the wall element [4]. In general the reversible cyclic load is defined by the following expression:

where:

g = angular deformation of wall,
d₁, d₂ = shortening or elongation measured on the diagonals,
L₁, L₂= initial length of diagonals
l_m, h_m _ are the width and height of the wall respectively.

And the total distortion (R_tot) or effective distortion (R_Eff) is calculated as:

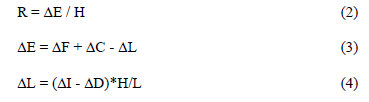
where:

R= effective drift of the wall.
DE= effective lateral displacement at top of the wall,
DL, DF, and DC _are defined in Fig. 3.
DI, DD _ are vertical displacements at ends in wall-slab joint,
H= distance between TD-01 y TD-08 (Fig 1(b))
L= distance between TD-04 y TD-05 (Fig 1(b))

 

5. Experimental and numerical results

5.1. Response to gravitational loading, experimental vs. analytical results

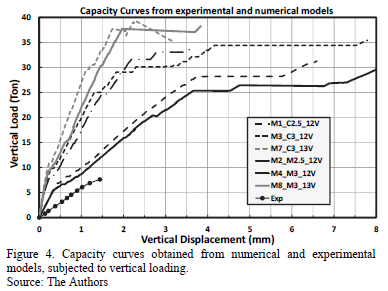
The code in the analytical models (Table 1) is defined as: M#_Mat#_#V. The M# indicates the model number. The Mat# indicates the material and length of the wall, for example M2.5 indicates that the wall is made out of masonry and has a length of 2.5 m, C indicates that the wall is made out of Concrete. The #V indicates the thickness of the slab, for example 12V indicates that the slab is 12 cm thick.

The capacity curve obtained from the experimental (Exp) specimen is compared with that of the numerical model (M2_M2.5_12V). The experimental system produced a minor stiffness value, as is shown in the curve. This can be explained due to the perfect fixed ends on the perimeter of the slab in the numerical model. However, in both curves the first cracking of the slab occurred at the same time. This happened at an approximate load value of 5.5 tons (Fig. 4). The numerical model was taken to failure mode, the first slab cracking occurred at 5.5 tons; the whole system exhibited linear behavior until the ultimate load of 25 ton was reached. From this point an almost elastic-perfectly-plastic "non-linear" behavior was observed (Fig. 4).

The numerical models M1_C2.5_V12 and M2_M2.5_12V differ in the wall material, _C#_ refers to concrete and _M#_ refers to masonry, as was previously explained. When their capacity curves are compared, they look very similar. This indicates that under vertical loading, no matter what material the wall is made of, the capacity of the whole structural system will almost remain the same. This is confirmed with the curves of the other two pairs of models shown in Fig. 4, which also portrayed the same behavior. Furthermore, whenever the wall is larger, for example 3 m (M3_C3_V12 and M4_M3_V12), both the capacity and the stiffness of the system were increased. Similarly, when the slab thickness was increased to 13 cm (M7_C2.5_V13 and M8_M2.5_V13), the ultimate capacity was also increased.

The stiffness is the same for loads less than 10 Tons. One of the results that we would like to highlight from the numerical analysis is that, for slab-wall models with a varied slab thicknesses, the ultimate capacity in the system was increased. The stiffness that was observed during the service conditions was also very similar, and, therefore a thicker slab does not guarantee a greater stiffness value while in service conditions.

5.2. Response to gravitational and lateral loading

The tested specimen was subject to a constant vertical load of 8 tons and 16 cycles of monotonic and cyclic horizontal loading. The load was applied with a hydraulic jack with the capacity to perform push and pull actions. The loading was controlled by the horizontal displacement at the top of the wall. The 16 cycles were applied in pairs (push and pull actions), from 0.5 mm to 12 mm; the last two cycles were asymmetric (14 mm and 27 mm), due to the limitation of the hydraulic jack in performing pull actions. The corresponding applied loads were above 11 Tons and 8.9 Tons in push and pull actions.

5.2.1. Displacement and rotation of the wall

Three locations - vertical displacements - under the specimen slab were measured during the test. These are the points TD05, TD03, TD04, which are along the centerline and right under the wall (Fig. 1). Due to the effect of horizontal loading, whenever the right transducer (TD05) climbed above the original reference line it generated rigid-body rotation of the wall (Fig. 3). The vertical displacement increased with every cycle from the beginning of the load. This indicated that due to vertical load intensity on the slab the overall structural behavior observed was non-linear. In every cycle, the slab suffered a displacement of 0.5 mm without returning to its initial position. This represented an approximate accumulated displacement of 9.5 mm at the end of the test.

5.2.2. Shear strains

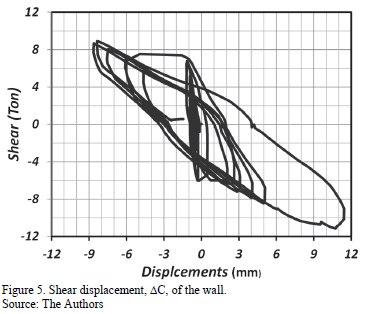
Rotation, g, of the wall due to shear deformation is calculated according to the strength of materials theory. Micrometers on wall diagonals did not record any deformation during the first six loading cycles; therefore, it can be concluded that the wall did not have any shear deformations in the first part of the loading process. It only suffered bending and rotation at the base due to slab rotation. However, during the seventh cycle, the diagonal micrometers (TD011 and TD012) began recording shear strains. Until the tenth cycle, the masonry wall exhibited linear behavior, after which the wall experienced non-linear deformations. Fig. 5 shows the hysteresis cycles of shear deformations on the wall.

5.2.3. Global and relative horizontal drifts

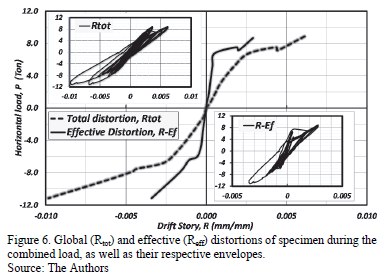
Fig. 6 shows the total distortions, R_tot, of the specimen, and the relative drift, R_Ef, which was calculated during the process of the combined load. In addition, it shows the envelopes of the hysteresis cycles, which are defined by a bilinear trend in the curves. The stiffness was calculated from the slopes of the curves; the stiffness of the slab-wall system was estimated as 11.25 Ton/cm, while the stiffness of the isolated wall (we removed the effect of the rotation as a rigid body) was computed to be 40.0 Tons/cm. This is 3.5 times larger than the wall supported on a flexible base, which is the case whenever the wall is placed in the middle of a two-way slab.

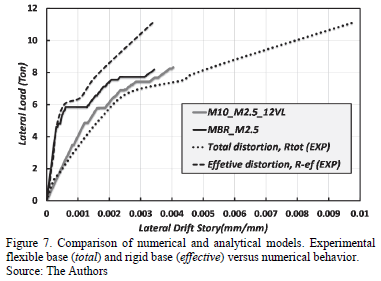
Fig. 7 compares the capacity curves of numerical models M10_M2.5_12VL (wall on flexible base) withMBR_M2.5 (wall on rigid base). We observed significant differences in the curves; even though the load capacity was close to 8 Tons, it is evident that the slopes are different. Stiffness values are also different, for a wall on a flexible base 14 Tons/cm was reached and the one on rigid base was computed as 40 Tons/cm. Numerical and experimental curves were compared, the slopes are very similar for all the models, and the stiffness values obtained in the tested specimen slab-walls were quite similar to those from numerical analysis.

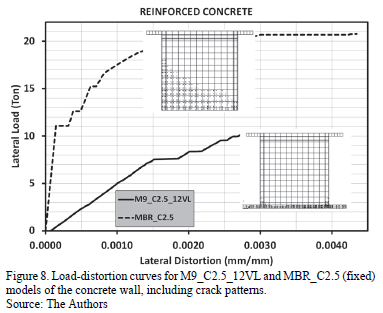
Results from numerical models that consider concrete walls (Fig. 8) show that the behavior is significantly different from the one observed in the masonry wall models. The capacity curves from numerical models M9_C2.5_12VL and MBR_C2.5 (fixed base), show a difference in the linear slopes for as many as 15 times; we computed 14.06 Tons/cm and 210 Tons/cm. However, the stiffness values for the masonry and concrete flexible models M10_M2.5_12VL and M9_C2.5_12VL are very similar, (14.06 Ton/cm vs. 11.25 Ton/cm). The flexibility of the slab does not allow the concrete wall to develop its full capacity and stiffness. This is one result that we would like to draw great attention to.

5.3. Analysis of crack patterns

The crack patterns of numerical models with masonry walls is very similar in both cases, regardless of how the wall is supported (flexible or fixed). This distribution of cracks is typical in confined masonry walls where the cracks are located in the diagonals of the wall. The numerical model cracks are very similar as the ones observed in the slab-wall prototype experimental test (Fig. 9).

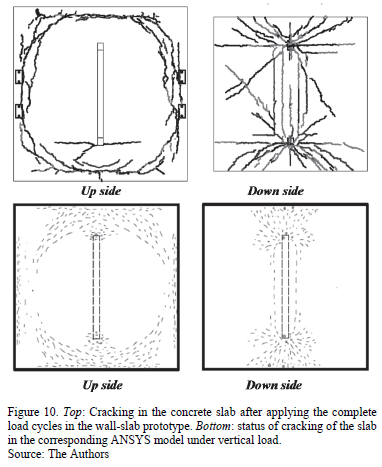
We also studied the pattern and distribution of cracking in the numerical models. In the case of concrete walls (Fig. 8), the crack pattern was quite different. The wall on the slab only had a few cracks, and the crack pattern observed on the wall supported on a rigid base was located in the tension zone (lower left corner) of the wall. The concrete wall on a rigid base developed its full shear capacity, while the wall on the transfer slab developed few shear deformation. This phenomenon was attributed to the rotations in the slab, which provoked a large decrease in the stiffness capacity of the whole system, Fig. 8. This condition is very critical for the slab, specifically in the areas located at the ends of the wall. In this area the slab had large cracks on its down side and sustained concrete crushing on the up side. This situation significantly reduces the slab capacity Fig. 10 shows the crack pattern on the up side of the slab(top left) and the crack pattern on the down side of the slab(top right).

5.3.1. Cracking in the slab

When a vertical load was applied to the specimen, the first cracks were observed at the edges of the slab, near the adjacent beams, and normal to the wall. However, at the end of the test, crack patterns at both sides of the slab was observed (Fig. 10 Top). Cracks in the up side of the slab were concentrated on the perimeter edges, and some cracks were observed at the edges of the wall (Fig. 10 Top-left). However, in the down side of the slab, concentrated cracks were observed along the line of the wall in horizontal and radial position. All the cracks had a common origin, which were the unions between the tie-columns and the slab. As a reference, Fig. 10 (bottom) shows the results of the numerical model in ANSYS with vertical loading.

 

6. Conclusions

In the first stage the specimen was subjected to a process of semi-cycles of increased vertical loading. We observed the first cracking of the concrete slab when the vertical load reached 5.8 Tons. The recorded deflection was 0.5 mm at the centerline of the slab; the load was very close to the design load. After the first stage, the specimen regained its elastic behavior. The numerical model of ANSYS also predicted the onset of cracking at the same load value.

Whenever a low horizontal load was applied, we observed that the stiffness of the slab-wall system was a third of the one observed for a wall on a fixed base. The wall had horizontal displacement mainly because of the slab bending (66%) and the wall bending (33%). The shear deformations were not measured.

During the combined loads process, we observed that the slab sustained deformation in such a way that, after each cycle, a residual deformation in the center line of the slab was growing bigger. The rate was 0.5 mm per cycle without returning to its initial position, due to the intensity of the constant vertical load and the increasing horizontal load.

In the combined loads process, the wall did not suffer shear strains during the first six loading cycles, and was only deformed by bending and rotation of the base, due to the bending of the slab. However, from the seventh cycle, the shear deformation started. Up to the tenth load cycle the behavior was elastic, and after that cycle we consider that the behavior was non-linear.

When the curves from the experimental model are compared to those from the numerical model with ANSYS, we observed an excellent correlation between the two analyzed conditions. The initial stiffness of the isolated wall is 3.5 times greater than the one in the slab-wall model. The concrete wall stiffness supported on a slab decreases by 15 due to the flexibility of the slab.

 

Acknowledgements

The authors would like to thank the partial support provided by the Secretaría de Obras del Gobierno del Distrito Federal (GDF, Mexico City) through conventions 212015 and 22611040.

 

References

[1] Gómez-Soberón, C., Gómez-Bernal, A., González-Cuevas, O., Terán, A. y Ruiz-Sandoval, M., Evaluación del diseño sísmico de estructuras nuevas ubicadas en la Colonia Roma del Distrito Federal. Proc. XVII Congreso Nacional de Ing. Sísmica, SMIS, Puebla, Méx. Nov. 2009.         [ Links ]

[2] Gomez-Bernal, A., Manzanares, D.A. y Juarez-Garcia, H. Interaction between shear walls and transfer-slabs, subjected to lateral and vertical loading Proc. Vienna Congress on Recent Advances in Earthquake Engineering and Struc. Dynamics. 447, pp. 28-30. Viena, Aut. Aug. 2013        [ Links ]

[3] Gómez-Bernal, A., Manzanares, D. y Juárez-García, H., Comportamiento de edificios discontinuos en altura y con pisos de transferencia. Proc. XVIII Congreso Nacional de Ingeniería Sísmica, SMIS, Veracruz, Ver. 2013.         [ Links ]

[4] Carrillo, J., Alcocer, S. y González, G., Deformation analysis of concrete walls under shaking table excitations. Revista DYNA, 79(174), pp. 145-155, 2012. ISSN 0012-7353. Medellín.         [ Links ]

[5] Gouveia, J.P. and Lourenço, P.B., Masonry shear walls subjected to cyclic loading: influence of confinement and horizontal reinforcement. Proc. Tenth North American Masonry Conference, St. Louis M. USA. Junio 2007.         [ Links ]

[6] Astroza, M. y Schmidt, M., Capacidad de deformación de muros de albañilería confinada para distintos niveles de desempeño, Revista de Ingeniería Sísmica, 70, pp. 59-75, 2002.         [ Links ]

[7] Preti, M., Migliorati, L. and Giuriani, E., Experimental testing of engineered masonry infill walls for post-earthquake structural damage control, Bulletin of Earthquake Engineering, 13(7), pp 2029-2049, 2015. DOI 10.1007/s10518-014-9701-2.         [ Links ]

[8] Meli, R., Mampostería estructural, la práctica, la investigación y el comportamiento sísmico observado en México. CENAPRED Reporte Seguridad sísmica de la vivienda económica, n17 julio, México, 1994.         [ Links ]

[9] Park, R. and Gamble, W.L., Reinforced Concrete Slabs, 2nd. Ed., John Wiley & Sons, Inc. 2000.         [ Links ]

[10] Vecchio, F. and Tang, K., Membrane action in reinforced concrete slab. Can. J. Civ. Eng. 17, pp. 686-697, 1990. DOI: 10.1139/l90-082        [ Links ]

[11] Reglamento de Construcciones del Distrito Federal. NTC de Mampostería. Gaceta Oficial del Gobierno del D.F. México, 2004.         [ Links ]

[12] Vargas-Arguello, O.S., Diseño, construcción y ensaye ante carga cíclica de un prototipo losa-muro a escala natural. Tesis de Maestría. Posgrado en Ing. Estructural, CBI - Universidad Autónoma de Mexico, Mexico, 2014.         [ Links ]

[13] Manzanares-Ponce, D.A., Comportamiento de edificios estructurados con losa de transferencia. Tesis de Maestría. Posgrado en Ing. Estructural, CBI - Universidad Autónoma de Mexico, Mexico, 2013.         [ Links ]

[14] Tickoo, S. and Singh, V., ANSYS 11.0 for Designers, CADCIM Technologies, 2009.         [ Links ]

 

A. Gómez-Bernal, received his BSc. in Civil Engineering in 1984 from the Universidad Autónoma Metropolitana-Azcapotzalco, Mexico, his MSc. in 1989 and his PhD. in 1989, both in Structural Engineering from the Universidad Nacional Autónoma de México, Mexico. From 1984 to 1994, he worked for consulting companies within the structural engineering sector in Mexico City. From 1992 up until the present he has worked for consulting companies and higher education research programs in Mexico. Currently, he is a professor in the structures area at the Materials Department in the Universidad Autónoma Metropolitana - Azcapotzalco. His research interests include: structural behavior in steel structures and their connections, vulnerability and seismic hazard, post-earthquake damage assessment of masonry and concrete structures, post-earthquake evaluation and damage recognition. ORCID: 000-0002-7131-1688.

D.A. Manzanares-Ponce, received his BSc. in Civil Engineering in 2006 from the Universidad Nacional Autonoma de Honduras and his MSc. in Structural Engineering from the Universidad Autonoma Metropolitana in Mexico City, MExico. From 2006 to 2010 he worked in the design, supervision and construction of roads and edifications. He has developed several pieces of research related to concrete precast slabs, prestressed concrete, the use of recycled concrete and sustainability in construction. Currently he works in Mexico at the Asociacion Nacional de Industriales de Vigueta Pretensada as the Technical Manager and is a structural engineering advisor in several companies. ORCID: 0000-0001-8534-8724

O.S. Vargas-Arguello, received his BSc. in Civil Engineering in 2011 and his MSc. in Structural Engineering all of them from the Universidad Autonoma Metropolitana in Mexico City, Mexico. ORCID: 0000-0002-1230-7865

E. Arellano-Méndez, received his BSc. in Civil Engineering in 2000 from the Universidad Autónoma Metropolitana - Azcapotzalco, Mexico his MSc. in Structural Engineering in 2005 from the Universidad Nacional Autónoma de México, and his PhD. in Structural Engineering in 2013 from the Universidad Autónoma Metropolitana - Azcapotzalco. ORCID: 0000-0001-7790-1104

H. Juárez-García, received his BSc. in Civil Engineering in 1986 from the Universidad Autónoma Metropolitana-Azcapotzalco (UAM-A), Mexico, his MSc. in Structural Engineering in 1990 from the Universidad Nacional Autónoma de México, and his PhD in Earthquake Engineering (Civil Engineering) in 2010 from the University of British Columbia, Canada. From 1986 to 1994, he worked for consulting companies within the structural engineering sector in Mexico City. From 1992 up until the present he has worked for consulting companies and higher education research programs in Mexico, Canada and the USA. Currently, he is a Professor in the Structures Area in the Materials Department in UAM-A. His research interests include: structural behavior due to earthquake loading, multi-risk hazard assessment, vulnerability and seismic hazard, post-earthquake damage assessment of masonry and concrete structures, post-earthquake evaluation and damage recognition. ORCID: 0000-0002-0432-6476

O.M. González-Cuevas, is a BSc. in Civil Engineer from the Universidad de Yucatán, Mexico. He undertook his masters' degree as well as his PhD in Structural Engineering at the Universidad Nacional Autónoma de México (UNAM), Mexico. Since 1974 he has been a Research-Professor at the Universidad Autónoma Metropolitana (UAM), Mexico. He was also President of this university from 1985 to 1989. Among other appointments he is a former President of the Academy of Engineering of Mexico and of the Mexican Society of Structural Engineering. He has written several textbooks related to "Fundamentals of Reinforced Concrete" and "Structural Analysis". His field of research is mainly reinforced and prestressed concrete structures. ORCID: 0000-0001-9214-042X