Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.82 no.194 Medellín nov./dez. 2015
https://doi.org/10.15446/dyna.v82n194.48179
DOI: http://dx.doi.org/10.15446/dyna.v82n194.48179
Numerical modelling of Alto Verde landslide using the material point method
Modelamiento numérico del deslizamiento Alto Verde usando el método del punto material
Marcelo Alejandro Llano-Serna a, Márcio Muniz-de Farias b & Hernán Eduardo Martínez-Carvajal c
a Faculty of Technology, University of Brasilia, Brasilia, Brazil. mallano@unb.br
b Faculty of Technology, University of Brasilia, Brasilia, Brazil. muniz@unb.br
c Faculty of Technology, University of Brasilia, Brasilia, Brazil. carvajal@unb.br
c Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. hemartinezca@unal.edu.co
Received: January 13th, 2015. Received in revised form: May 7th, 2015. Accepted: September 25th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
A huge landslide took place at Alto Verde residential complex at the end of 2008 in the city of Medellin, Colombia, claiming the lives of twelve people and destroying six houses. Landslides are characterized by large deformations in the soil mass. This study used the material point method (MPM), a particle-based method that takes advantage of a double Lagrangian-Eulerian discretization. This approach provides a robust framework that enables the numerical simulation of large strains, without mesh entanglement issues that are common with the Finite Element Method. The numerical model proposed here assumes simplifications of the geotechnical, morphological and structural buildings conditions on the site. Nevertheless, the final numerical deformed configuration described the geometric features observed in the field successfully. The result allows applications such as the design of barriers, risk assessment or determination of a minimum safe distance for a building from a slope susceptible to landslides.
Keywords: Alto Verde; material point method; debris flow; large strains.
Resumen
Finalizando el año 2008 en la ciudad de Medellín, Colombia, ocurrió un deslizamiento de tierra en la urbanización Alto Verde provocando la muerte de doce personas y la destrucción de seis viviendas. Los deslizamientos se destacan por el elevado nivel de deformaciones en una masa de suelo. El presente trabajo utilizó el método del punto material (MPM), método basado en partículas que utiliza una doble discretización Lagrangiano-Euleriana. La doble discretización genera un marco numérico robusto que permite la simulación de grandes distorsiones. El modelo numérico planteó una simplificación de las condiciones geotécnicas, morfológicas y estructurales de las edificaciones envueltas en Alto Verde. El estado de deformación final de la simulación se acomodó satisfactoriamente a las características geométricas finales observadas en campo. Los resultados obtenidos generan aplicaciones como el diseño de barreras, análisis de riesgo o la determinación de la distancia mínima de retiro a una ladera susceptible de deslizamiento.
Palabras clave: Alto Verde; método del punto material; flujo de escombros; grandes deformaciones.
1. Introducción
La historia de un movimiento en masa según Skempton y Hutchinson [1] está compuesta por tres etapas: (i) deformaciones previas a la ruptura, (ii) la ruptura como tal y (iii) los desplazamientos posteriores a la ruptura. Adicionalmente, la pérdida de resistencia al esfuerzo cortante durante la ruptura determinará la velocidad del movimiento, la cual involucra cambios cinemáticos del deslizamiento a flujo o caída. Esto es relevante porque definirá el comportamiento y destructividad del evento [2].
Los deslizamientos urbanos son detonados principalmente por cambios hidrológicos, ambientales y principalmente antropogénicos, tales como lluvias fuertes, terremotos y actividades humanas. Los efectos adversos de los deslizamientos urbanos se han hecho más severos debido al crecimiento poblacional incontrolado en regiones de ladera. Consecuentemente, los riesgos que surgen de estos desarrollos urbanos en áreas susceptibles a deslizamientos están aumentando a pesar de los progresos en la aplicación de medidas de mitigación.
El análisis de la estabilidad del talud y el inicio del deslizamiento puede ser abordado mediante el uso de métodos clásicos en la ingeniería geotécnica, tales como el método de equilibrio límite o el ampliamente conocido método de los elementos finitos (MEF). Sin embargo para modelar el comportamiento del suelo durante un deslizamiento se debe utilizar un método numérico capaz de manejar grandes deformaciones [3].
Actualmente el MEF es el método más utilizado para el cálculo de deformaciones en problemas de geotecnia. A pesar de esto el método presenta fuertes limitaciones cuando la solución involucra grandes distoriones. Para extender el MEF a la simulación de grandes desplazamientos es necesario el uso de tensores de grandes deformaciones y la actualización de la discretización del sólido deformado. Este proceso de mapeamiento y relocalización de variables de estado produce pérdidas de información generando imprecisiones en la solución final [4].
Como respuesta a las limitaciones del MEF surgió el método del punto material (MPM) [5-7]. En este método se discretiza el dominio físico del problema en un número de puntos sobre los cuales se almacenan las propiedades del medio y las variables de estado. La interacción entre los diferentes puntos y el desarrollo de las tensiones y deformaciones se obtienen al rastrear éstas gracias a una malla computacional de fondo donde se resuelven las ecuaciones de movimiento. Al mismo tiempo la información se almacena en los puntos materiales (PM), la malla de cálculo es indeformable y se puede utilizar durante todo el análisis.
El MPM ha sido utilizado con éxito en la simulación de problemas relacionados a estabilidad de laderas y taludes. Entre ellos se destacan: El cálculo de estados de tensión [8], análisis multifásicos de taludes sometidos a cargas cíclicas [9], estudio paramétrico considerando la interacción entre deslizamientos con estructuras rígidas [10], problemas de flujos de detritos (Debris-flows) en tres dimensiones incorporando obstáculos en su trayectoria [11,12] y determinación de superficies de ruptura y análisis acoplados [13-15]. El único caso real simulado del que se tiene conocimiento corresponde a un deslizamiento cerca al pueblo de Lønstrup, Dinamarca, en el año de 2008 [3].
El 16 de noviembre de 2008 se presentó la falla de un talud en el barrio Alto Verde en la ciudad de Medellín, Colombia, con un volumen estimado entre 13000 m³ y 25000 m³. El mecanismo inicial, probablemente de tipo rotacional, evolucionó a un mecanismo de tipo Debris-flow con alto poder destructivo. El talud se había construido en una unidad superficial geológicamente conocida en el ambiente local como Suelo Residual de Dunita. El deslizamiento y flujo destruyeron a su paso seis casas, dejando un saldo de doce personas muertas y cuantiosas pérdidas económicas [16,17].
En este artículo se presenta la simulación del deslizamiento de Alto Verde utilizando el MPM, incluyendo la visualización y reproducción fiel de los cambios en la geometría del sitio durante y después del evento, además del cálculo de variables como la velocidad del movimiento en masa, lo que constituye un avance pionero en este tipo de análisis. Finalmente, la estimación de la velocidad y la energía cinética abre la posibilidad de resolver problemas relacionados con la cuantificación de la vulnerabilidad de estructuras y personas sometidas al impacto de deslizamientos.
2. Método del punto material
Durante este trabajo se utilizó como referencia la formulación presentada por Buzzi et al. [18]. La notación tensorial es definida de la siguiente forma: los tensores son representados por una letra y su orden es demarcado por la cantidad de líneas (-), un punto (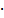 ) simboliza una contracción simple, dos puntos (:) simbolizan una contracción doble y el símbolo (
) simboliza una contracción simple, dos puntos (:) simbolizan una contracción doble y el símbolo (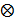 ) es el producto diádico o tensorial.
) es el producto diádico o tensorial.
2.1. Formulación
La ecuación de campo que gobierna el balance de momento lineal en un medio continuo para satisfacer las condiciones de equilibrio dinámico se pueden representar utilizando notación tensorial así:
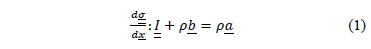
en la ec. 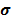 representa el tensor de tensiones de segundo orden,
representa el tensor de tensiones de segundo orden, 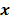 es el vector de posición de un punto,
es el vector de posición de un punto, 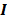 se refiere al tensor identidad de segunda orden, r el campo de densidad escalar,
se refiere al tensor identidad de segunda orden, r el campo de densidad escalar, 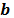 tensor de primer orden con las fuerzas de cuerpo y externas actuantes y
tensor de primer orden con las fuerzas de cuerpo y externas actuantes y 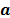 es el vector de aceleración.
es el vector de aceleración.
Para obtener la forma débil del balance de momento lineal, la ec. se multiplica por funciones de prueba arbitrarias de la forma 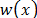 que por medio del método de residuos ponderados es integrado sobre todo su dominio (V) y se obtiene:
que por medio del método de residuos ponderados es integrado sobre todo su dominio (V) y se obtiene:
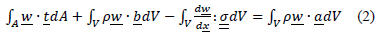
donde 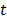 define las fuerzas de tracción en la superficie de una región A.
define las fuerzas de tracción en la superficie de una región A.
El campo de densidades, tensiones y aceleraciones de cada PM se discretiza por medio de funciones de característica aplicadas en la partícula de la siguiente forma:
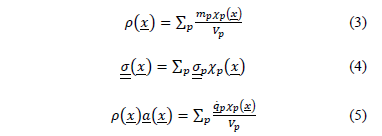
aquí el subíndice p se refiere a cada punto material donde mp es la masa, 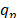 su momento lineal,
su momento lineal, 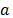 la aceleración y
la aceleración y 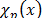 es la función de característica en la partícula. Estas funciones se requieren para dividir la unidad referente a la configuración inicial, como se puede ver en la siguiente ecuación.
es la función de característica en la partícula. Estas funciones se requieren para dividir la unidad referente a la configuración inicial, como se puede ver en la siguiente ecuación.
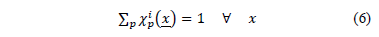
Las funciones de peso y sus derivadas respecto a la posición son discretizadas de acuerdo a la malla computacional mediante las siguientes expresiones:
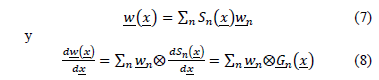
Reemplazando las ecs. - en la ec. se obtiene la ecuación de gobierno discreta:
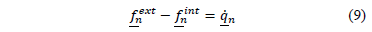
donde los vectores de fuerzas externas son:
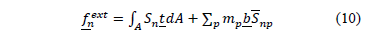
y el vector de fuerzas internas en término de las tensiones de Kirchhoff es:
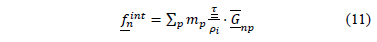
Como fue discutido por Nairn y Guilkey [19] la forma de la ec. es conveniente porque evita tener que calcular la densidad o el volumen de cada partícula en cada intervalo de tiempo.
Los términos 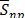 y
y 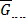 en las ecs. - representan la influencia de las funciones de forma y sus gradientes respectivamente, estos pueden ser calculados a partir de:
en las ecs. - representan la influencia de las funciones de forma y sus gradientes respectivamente, estos pueden ser calculados a partir de:
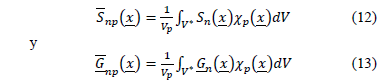
donde el dominio de integración 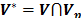 es el volumen que soporta las funciones características. Las cuales son uno de los avances más relevantes que ha sufrido el MPM desde su formulación inicial [7].
es el volumen que soporta las funciones características. Las cuales son uno de los avances más relevantes que ha sufrido el MPM desde su formulación inicial [7].
2.2. Procedimiento de cálculo
El problema es integrado dinámicamente en el tiempo por medio de un esquema de diferencias finitas en avance donde la información es almacenada en los PMs. Después que el sólido en análisis es discretizado por un conjunto de puntos materiales, p, la masa de la malla de fondo, mn, y su momento lineal, 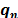 , son inicializados por medio de las funciones de forma,
, son inicializados por medio de las funciones de forma,
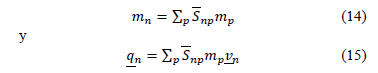
El incremento de deformaciones es calculado para cada vértice al inicio y al final de cada intervalo de tiempo utilizando el gradiente de velocidades y la media ponderada de los volúmenes de las partículas contribuyentes así:
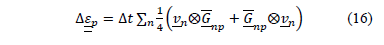
donde la matriz 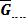 se calcula con base en la ec. y el incremento de las tensiones se obtiene por medio del modelo constitutivo adoptado para cada partícula. Para actualizar la posición y velocidades a partir de los vértices de la malla se utilizan las siguientes expresiones:
se calcula con base en la ec. y el incremento de las tensiones se obtiene por medio del modelo constitutivo adoptado para cada partícula. Para actualizar la posición y velocidades a partir de los vértices de la malla se utilizan las siguientes expresiones:
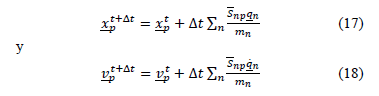
El algoritmo completo para resolver el método adoptado puede ser consultad en Buzzi et al. [18].
2.3. Algoritmo de contacto
Para modelar la interacción entre dos materiales, el flujo de detritos y la topografía del terreno por ejemplo, es necesaria la implementación de un algoritmo de contacto. Las bases del algoritmo presentado aquí fueron establecidas por Bardenhagen et al. [20] y mejoradas por Lemiale et al. [21] y Nairn [22]. Para explicar el mecanismo se asume la existencia de dos materiales a y b que interactúan en un determinado nodo n de la malla. Las velocidades de cada material en el nodo son 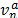 y
y 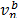 respectivamente. También se define un vector normal,
respectivamente. También se define un vector normal, 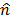 , positivo cuando el material a se dirige hacia el material b. El cálculo de este vector es el punto crucial del algoritmo de contacto [22]. Posteriormente, el momento lineal debe ser ajustado mediante la implementación de las características del contacto.
, positivo cuando el material a se dirige hacia el material b. El cálculo de este vector es el punto crucial del algoritmo de contacto [22]. Posteriormente, el momento lineal debe ser ajustado mediante la implementación de las características del contacto.
Una vez que la dirección del vector normal es determinada, se debe detectar la existencia del contacto, como es descrito en [20-22].
Para un caso de contacto friccional simple se emplean fuerzas normales y tangenciales descritas en las siguientes expresiones.
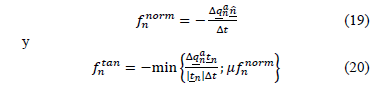
donde Dt es el intervalo de tiempo, 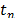 es un vector tangente al vector normal
es un vector tangente al vector normal 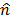 en la dirección de deslizamiento y µ es el coeficiente de fricción de Coulomb.
en la dirección de deslizamiento y µ es el coeficiente de fricción de Coulomb.
3. Caso de análisis: Deslizamiento de Alto Verde
El deslizamiento de Alto Verde ocurrió en la región suroccidental del municipio de Medellín- Colombia, durante el mes de noviembre de 2008. El evento afectó una urbanización residencial que lleva el mismo nombre, compuesta por 16 viviendas unifamilares construidas a lo largo de un trecho de vía central.
El evento se produjo durante una época de alta pluviosidad, la cual fue calificada como la más crítica de los últimos sesenta años [17]. Entre las causas que originaron el deslizamiento fueron citadas: (i) el aumento de los niveles freáticos sobre la vertiente del talud, (ii) infiltración superficial originada por la presencia de un tanque de tratamiento de agua cerca de la corona, (iii) la construcción inadecuada del talud y (iv) intervención antrópica en la parte alta de la ladera [16]. De acuerdo con AMVA [16] los registros de precipitación indicaron un acumulado de 110 mm en los 15 días anteriores al evento.
En la Fig. 1 se observa una imagen del complejo residencial Alto Verde en mayo de 2008, seis meses antes de la ocurrencia del deslizamiento. Por otra parte, al lado derecho de la misma figura se muestra la situación en 2011, después de la ejecución de obras de estabilización. La comparación entre ambas imágenes da una idea clara del tamaño del deslizamiento y de su relación con las estructuras afectadas.
El lado izquierdo de la Fig. 2 muestra la situación del evento el mismo día de su ocurrencia. En contraste, el lado derecho muestra la situación dos años después, ya ejecutados trabajos de estabilización.
3.1. Características geométricas y ambiente geológico-geotécnico
Los taludes que conformaban el costado posterior de la unidad residencial tenían alturas variables que alcanzaban hasta 18 m. Las condiciones que desencadenaron la tragedia corresponden al talud de máxima altura y 60° de inclinación como ha sido reconocido en trabajos técnicos previos [16,17].
El perfil de suelo del sitio está compuesto por una capa de andosol (ceniza volcánica intemperizada) de un espesor aproximado de 2 metros sobreyaciendo a una capa de suelo residual de Dunita (probablemente fallada, por lo cual fue llamado de Brecha de Dunita) de 15 metros de espesor. El basamento de esta secuencia simple está conformado por la roca brechoide en condición sana. El deslizamiento afectó los horizontes de andosol y de suelo residual superiores, por lo que se resalta su carácter superficial.
Igualmente, el mecanismo observado fue de tipo rotacional tal como se puede verificar en la fotografía de la Fig. 3.
La profundidad a la que se encontró el nivel de aguas freáticas fue de 14 metros cerca de la corona del talud y de 7 metros en la región de acumulación [16,17]. Las condiciones aquí descritas y la configuración general de la urbanización en el eje A'-A mostrado en la Fig. 1 se encuentran esquematizadas en la Fig. 4.
3.2 Modelo numérico
El modelo numérico consideró algunas simplificaciones buscando reducir el tiempo computacional a valores razonables.
En primer lugar la representación bidimensional en un estado plano de deformaciones de un problema que efectivamente ocurrió bajo condiciones tridimensionales. La segunda y más importante simplificación se basa en el hecho de que como se mencionó anteriormente este trabajo se centra en la reproducción del fenómeno de flujo de escombros y no en la reproducción del mecanismo inicial de falla. Dicho mecanismo ya fue publicado [17] y verificado por los autores en análisis independientes con técnicas convencionales de equilibrio límite y mediante la observación de levantamientos topográficos posteriores a la ocurrencia del deslizamiento. Procedimientos similares al aquí descrito fueron usados y reportados por Sawada et al. [25].
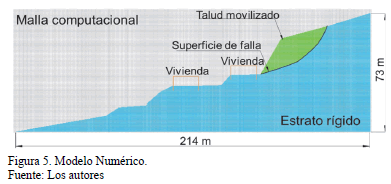
En la Fig. 5. El estrato rígido representa la masa de suelo que no se movilizó durante el incidente, mientras que el talud movilizado representa la masa de suelo que se desplaza ladera abajo. La última simplificación geométrica se refiere a la estructura de las viviendas. En primer lugar la profundidad de las fundaciones se asumió arbitrariamente ya que se espera una falla por tensión cortante directa y su longitud no tiene efecto. En segundo lugar la superestructura se simplificó buscando reducir el tiempo computacional. Esta es una suposición razonable considerando que el objeto de análisis en este trabajo se centra sobre la evolución geométrica del movimiento en masa desde el punto de vista geotécnico.
Las principales características geométricas del modelo se encuentran resumidas en la Tabla 1.
Para resolver el modelo numérico se utilizó el código abierto NairnMPM 8.1.0 [26]. Como fue mencionado anteriormente el estrato subyacente se consideró como un único material indeformable, es decir de rigidez infinita. Sin embargo este material puede interactuar con los demás materiales por medio de las leyes friccionales de contacto descritas en el capítulo anterior. Por otro lado la masa de suelo que se desliza y las estructuras fueron modeladas como materiales elásticos perfectamente plásticos con criterio de ruptura von Mises.
El análisis se lleva a cabo en términos de tensiones totales en lugar de efectivas porque el deslizamiento se asume que ocurre bajo condiciones no drenadas debido a la velocidad con que se producen las deformaciones.
Una de las limitaciones que surgen en los modelos de grandes deformaciones es que los parámetros constitutivos referente a los materiales que se usan y reportan usualmente en la ingeniería civil se refieren a ensayos sometidos a pequeñas deformaciones. Esto se justifica porque las obras que se diseñan normalmente operan bajo estas condiciones. Teniendo esto en cuenta se reportan en la Tabla 2. los parámetros utilizados para los materiales considerados en la simulación.
Los valores de los parámetros usados se determinaron con base en los resultados reportados por Gómez et al. [17], los cuales fueron ajustados por medio de retroanálisis, buscando una semejanza en la configuración final observada y el modelo numérico aquí usado.
El coeficiente (m) que gobierna la ley de contacto friccional entre el material que compone el deslizamiento y el estrato rígido es obtenido mediante la expresión propuesta por Davies [27].
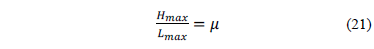
donde Hmax y Lmax son la distancia vertical y horizontal entre la corona del deslizamiento y su lóbulo frontal. La ec. fue calculada de acuerdo a los datos reportados por Gómez et al [17] y el resultado se encuentra reportado en la Tabla 3.
Por otro lado, debido a que no se contó con información sobre las fundaciones se asumió un coeficiente elevado entre la estructura y el suelo de fundación para evitar una falla de tipo arrancamiento. Entre las partículas del deslizamiento y las estructuras se consideró la inexistencia de fricción. Ver Tabla 3.
4. Resultados
Para la simulación de este trabajo se utilizó un computador de escritorio con 4 procesadores Intel i7-2600k, y CPU@3.4GHz. El intervalo de tiempo adoptado para la simulación fue de Dt= 2.94.10-4 s con lo cual el tiempo total de simulación fue de 40 horas. Este tiempo de análisis puede ser disminuido a 10 horas por medio de la paralelización del código y el uso de un cluster computacional de 9 nodos intel i7-870 2.93 GHz CPU, 16 GB de memoria RAM y 1 TB de disco duro.
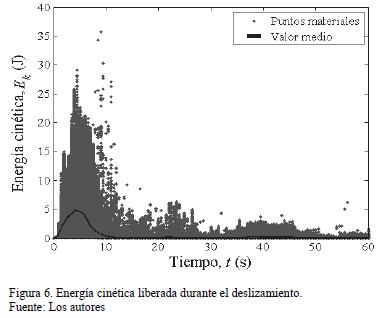
La simulación del deslizamiento comienza a partir del mecanismo de falla indicado t=0 s, instante en el cual se aplica la aceleración de la gravedad al sistema. La simulación del deslizamiento reproduce los primeros 60 segundos de evolución del movimiento en los cuales es posible acompañar, entre otras variables, la energía cinética de cada uno de los puntos. En la Fig. 6 se presenta gráficamente la energía cinética calculada para todos los puntos movilizados (color verde en la Fig. 7) durante el tiempo simulado.
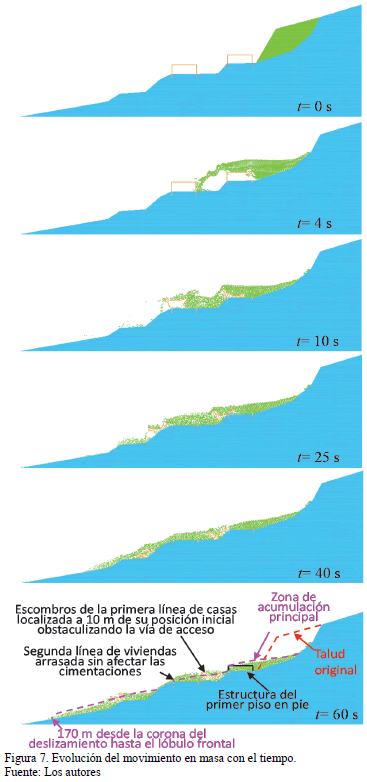
De acuerdo a los resultados de energía cinética (Ver Fig. 6), es posible notar que el momento más crítico se presentó a los 4 s aproximadamente en donde se observa claramente un pico de energía a partir del cual hay disminución de la misma. En la Fig. 7 se observa que para el tiempo t=4 s el frente de avance impacta la segunda estructura (nivel topográfico inferior) después de haber pasado por encima de la primera casa (nivel topográfico superior), la cual colapsa.
El valor de energía cinética promedio máximo estimado es de aproximadamente 5.0 J correspondiente a una velocidad de 8.5 m/s. En la misma Fig. 7 se muestran diferentes momentos de la simulación en los cuales se puede observar la evolución del flujo. Pasados 10 s la energía cinética se reduce drásticamente, justo después del colapso del segundo nivel de casas las cuales contienen en gran medida el avance del movimiento (Ver Fig. 7). A partir de este punto la velocidad del movimiento es baja con algunos picos a los 25 y 40 s atribuidos al efecto de aceleración impuesto apenas por los escalones topográficos del terraceo del terreno.
5. Discusión
La simulación realizada se ejecutó a partir de un retroanálisis del mecanismo de falla inicial para ajuste de las propiedades geotécnicas del deslizamiento en masa. Los valores de estos parámetros son compatibles con los que han sido publicados en la literartura para el mismo caso analizado (Ver Tabla 2.). Con la información topográfica disponible fue posible reproducir la trayectoria del debris-flow en una distancia de 170 metros desde la corona hasta el lóbulo frontal que alcanzó el deslizamiento real [17].
De la misma forma es posible resaltar que la simulación reprodujo bien la configuración real del flujo, coincidiendo con las descripciones encontradas en los trabajos técnicos previos y en las fotografías sobre los sitios referentes a las zonas de acumulación.
En la etapa final, 60 s, en la Fig. 7 fueron esquematizadas las descripciones encontradas en la literatura [16, 17] en donde la zona de acumulación, la localización de escombros de la primera línea de casas alcanzada por el deslizamiento que obstaculizó la vía de acceso, el arrancamiento de la superestructura de las casas en el nivel topográfico inferior y la distancia máxima desde la corona del talud hasta el lóbulo frontal fueron reproducidas exitosamente. Sin embargo, las descripciones técnicas también relatan que la superestructura del primer piso de las casas en el nivel superior permaneció de pie, fenómeno que no presenta el modelo aquí descrito.
Desde un punto de vista cualitativo se determinó que la ruptura tajante del talud suponía un movimiento extremadamente rápido con velocidades en términos de metros por segundo, AMVA [16]. Esta información fue validada al calcularse una velocidad máxima media del movimiento de 8.5 m/s.
Todas las estructuras impactadas por el deslizamiento sufrieron una pérdida de servicio total, con excepción de una caseta de vigilancia, cuyos daños fueron parciales (Fig. 8). De acuerdo con el glosario de la sociedad internacional de mecánica de suelos e ingeniería geotécnica [28], la vulnerabilidad es el grado de pérdida de un elemento dado o conjunto de elementos dentro del área afectada por un deslizamiento, y se expresa en una escala de 0 (sin pérdidas) a 1 (pérdida total).
Para propiedades, la pérdida se estima como el costo de los daños en relación al valor de la propiedad. La estimación de la vulnerabilidad de estructuras y personas amenazadas por deslizamientos es generalmente cualitativa, altamente subjetiva y en muchos casos basada únicamente en registros históricos [29]. Trabajos recientes [30-33] han propuesto marcos teóricos para la evaluación cuantitativa de la vulnerabilidad física de estructuras en función de la intensidad del deslizamiento y de la resistencia estructural de los edificios expuestos.
El modelo propuesto por Li et al. [30] para el cálculo de la Vulnerabilidad, V, se basa en la aplicación de la siguiente expresión:
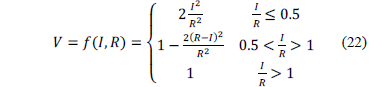
en la cual I es la intensidad del deslizamiento y R es la resistencia del elemento en riesgo. Ambas variables son adimensionales. La intensidad del deslizamiento puede expresarse de diversas maneras mediante alguna de las siguientes variables, o combinación de ellas: velocidad, energía, volumen y/o espesor del material movilizado.
Según Li et al. [30] en las estructuras impactadas por deslizamientos la intensidad del evento puede ser cuantificada en función de la intensidad dinámica que depende de la velocidad del flujo y de su profundidad, de acuerdo con las siguientes ecuaciones:
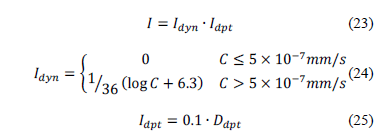
con: Idyn=Factor de intensidad dinámica; Idpt=Factor de espesura de detritos; C=Velocidad promedio del flujo de detritos (en mm/s) y Ddpt=Espesor del flujo de detritos (en metros) en el punto de impacto con la estructura.
Los mismos autores proponen que la resistencia física estructural (Rstr) depende de cuatro factores: Profundidad de la fundación (xsfd), tipología estructural (xsty), grado de mantenimiento de la estructura (xsmn) y su altura (xsht); de acuerdo con:
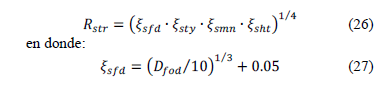
Los tres factores restantes dependen de la tipología estructural (xsty), estado de mantenimiento de la estructura (xsmn) y de un factor de resistencia dependiente de la altura de la estructura (xsht). Los valores de estos factores se encuentran tabulados por Li et al. [34] y para el caso específico de este trabajo asumen: xsty= 1.3, xsmn= 1.5 y xsht= 0.9.
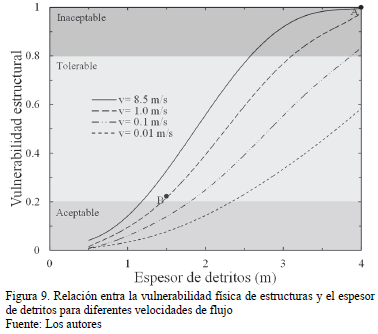
Considerando entonces el modelo de vulnerabilidad y los valores presentados, se estimó la resistencia física de las estructuras impactadas. La estimativa de la vulnerabilidad para estas estructuras dependerá entonces del espesor de la capa de detritos y de la velocidad del flujo. La Fig. 9 presenta la relación entre la vulnerabilidad y el espesor de la capa de detritos para diferentes velocidades. La velocidad de referencia usada fue de 8.5 m/s, que corresponde a la máxima velocidad promedio estimada en la simulación numérica.
Valores adicionales de velocidades fueron usados para visualizar el efecto de esta variable en el comportamiento de la vulnerabilidad. Los valores adicionales usados son: 1 m/s, 0.1 m/s y 0.01m/s. A partir de las observaciones fotográficas y de la propia simulación se estima en 4 m el espesor promedio máximo del deslizamiento, es decir, el espesor calculado a lo largo de la sección más crítica. De esta forma, el punto A en la Fig. 9 representa la vulnerabilidad de las casas impactadas por el deslizamiento. El valor estimado de la vulnerabilidad es 1 indicando, tal como realmente ocurrió, destrucción total de la estructura.
Por otra parte, estimativas realizadas para la caseta de vigilancia mostrada en la Fig. 8 indican un valor de vulnerabilidad de 0.2. Esto con base en la suposición de una velocidad media de 1 m/s, la cual es justificable si se tiene en cuenta que la caseta se localiza en el flanco derecho del deslizamiento donde las velocidades de flujo y espesor de detritos son menores (estimada en 1.5 m. Fig. 8). El punto B en la Fig. 9 representa la vulnerabilidad de la caseta, indicando un grado de pérdida de 20% en su funcionalidad estructural, lo cual corresponde a las observaciones de campo.
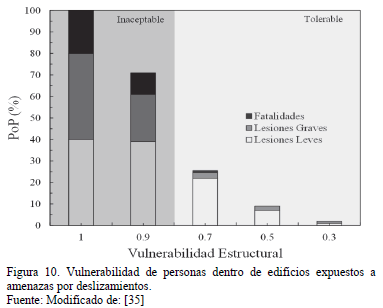
Ragozin and Tikhvinsky [35] analizaron la vulnerabilidad de personas dentro de edificios expuestos a amenaza por deslizamientos. La Fig. 10 presenta la probabilidad de que una persona (PoP) dentro de un edifício sufra lesiones de diferentes niveles, dependiendo de la vulnerabilidad física del edificio. Según los mismos autores, para una vulnerabilidad física estructural de 0.8, serias lesiones pueden esperarse en las personas dentro de la estructura. Para lesiones leves (heridas temporales) la vulnerabilidad estructural recomendada debe ser del orden de 0.2.
En la Fig. 9 se han representado los límites de 0.2 y 0.8 para las vulnerabilidades estructurales, definiendo como aceptable V< 0.2, tolerable el intervalo 0.2< V< 0.8 e inaceptable V> 0.8.
De esta forma, es posible deducir que para el caso de Alto Verde, todas las estructuras que sufrieron el impacto del flujo con más de 2.5m de altura de detritos, están dentro de la clasificación de vulnerabilidad inaceptable, lo cual fue verificado para las seis casas que fueron destruidas. Solamente las zonas del deslizamiento que tuvieron velocidades muy bajas (0.1 m/s o menores) indicarían valores de vulnerabilidad tolerables para los espesores de detritos que realmente ocurrieron (entre 2 y 4 m).
Zonas con velocidades moderadas (del orden de 1 m/s), como es el caso de la caseta de vigilancia, producen vulnerabilidades cerca de un intervalo aceptable con espesores de detritos del orden de 1.5 m o menores.
Finalmente, los autores gustaríamos de enfatizar que las tragedias por deslizamientos en la ciudad de Medellín han sido tradicionalmente asociadas a la ocurrencia de épocas lluviosas intensas. No obstante, tal como fue observado por Muñoz et al. [36] en taludes de carreteras en los alrededores de Medellín, aunque existe una gran propensión natural de las laderas de la ciudad a presentar deslizamientos, no es apenas la lluvia la responsable por el gran número de estos eventos, sino la práctica geotécnica local. Los referidos autores observaron que una gran cantidad de pequeños y moderados deslizamientos son deflagrados claramente por acciones antrópicas.
6. Conclusiones
El objetivo de este trabajo fue verificar la posibilidad de utilizar el MPM como una herramienta para describir los fenómenos asociados a deslizamientos de tierra. Para tal fin se definió un caso de estudio bien documentado que permitió el retro-análisis de las características de grandes deformaciones aquí detalladas.
A pesar de las simplificaciones respecto a modelos constitutivos y geometría fue posible establecer que las descripciones encontradas en la literatura sobre el estado final del deslizamiento, zonas de acumulación y condiciones de las estructuras describieron adecuadamente el flujo de tierra que ocurrió en Alto Verde.
El MPM permitió calcular la velocidad, energía cinética y alcance del deslizamiento. Este tipo de información es fundamental y permite el análisis de riesgo en taludes en zonas urbanas, el diseño de estructuras de barrera ante flujos de escombros, o determinar distancias de retiro a taludes con probabilidad de ruptura alta. El modelo de análisis cuantitativo de la vulnerabilidad física usado mostró valores compatibles con las observaciones de campo.
Curvas como las presentadas en la Figura 9 pueden ser usadas por las autoridades encargadas de la administración de ciudades susceptibles a deslizamientos, para definir criterios de aceptabilidad de proyectos urbanísticos en laderas. Esta metodología, combinada con análisis de confiabilidad de taludes y laderas, se muestra como una herramienta prometedora para evolucionar eficientemente en los proceso de análisis, evaluación y gestión de riesgos asociados a deslizamientos.
La forma como se abordan actualmente las metodologías de diseño de taludes en la práctica local y, más importante aún, la forma como dichas metodologías están involucrando el factor de la vulnerabilidad estructural y la confiabilidad en el marco de la normativa vigente debe ser revisada.
Es responsabilidad de los administradores locales establecer códigos modernos que lleven en cuenta criterios de aceptabilidad basados en análisis de riesgo y no apenas en estimativas de la amenaza.
Agradecimientos
Los autores de este trabajo gustarían de agradecer a la Coordinación de Perfeccionamiento de Personal de Nivel Superior (CAPES) y el Consejo Nacional de Investigación (CNPq) del gobierno Brasileño por el apoyo económico para la ejecución de este trabajo.
Referencias
[1] Skempton, A.W. and Hutchinson, J., Stability of natural slopes and embankment foundations, Proc. 7th Int. Conf. on Soil Mech. and Found. Eng. Mexico. State-of-art Vol. P, pp. 3-35, 1969. [ Links ]
[2] Hungr, O., Leroueil, S. and Picarelli, L., The Varnes classification of landslide types, an update, Landslides, 11(2), pp. 167-194, 2013. DOI: 10.1007/s10346-013-0436-y [ Links ]
[3] Andersen, S. and Andersen, L., Material-point-method analysis of collapsing slopes, Proceedings of the 1st International Symposium on Computational Geomechanics (COMGEO I), pp. 817-828, 2009. [ Links ]
[4] Al-Kafaji, I.K.J., Formulation of a dynamic material point method (MPM) for geomechanical problems, PhD. Thesis, Stuttgart University, Stuttgart, Germany, 2013. [ Links ]
[5] Sulsky, D., Chenb, Z. and Schreyer, H.L., A particle method for history-dependent materials, Comput. Methods Appl. Mech. Eng., 118, pp. 179-186, 1994. DOI: 10.1016/0045-7825(94)00033-6 [ Links ]
[6] Sulsky, D., Zhou, S.J. and Schreyer, H.L., Application of a particle-in-cell method to solid mechanics, Comput. Phys. Commun., 87, pp. 23-252, 1995.DOI: 10.1016/0010-4655(94)00170-7 [ Links ]
[7] Bardenhagen, S.G. and Kober, E.M., The generalized interpolation material point method, Tech Sci. Press, 5(6), pp. 477-495, 2004. DOI: 10.3970/cmes.2004.005.477 [ Links ]
[8] Beuth, L., Wieckowski, Z. and Vermeer, P.A., Solution of quasi-static large-strain problems by the material point method, Int. J. Numer. Anal. Meth. Geomech., 35, pp. 1451-1465, 2011. DOI: 10.1002/nag.965 [ Links ]
[9] Jassim, I., Stolle, D. and Vermeer, P., Two-phase dynamic analysis by material point method, Int. J. Numer. Anal. Meth. Geomech., 37 , pp. 2502-2522, 2013. DOI: 10.1002/nag.2146 [ Links ]
[10] Andersen, S. and Andersen, L., Modelling of landslides with the material-point method, Comput. Geosci., 14, pp. 137-147, 2010. DOI: 10.1007/s10596-009-9137-y [ Links ]
[11] Numada, M., Konagai, K., Ito, H. and Johansson, J., Material point method for run-out analysis of earthquake-induced long-traveling soil flows, JSCE J. Earthq. Eng., 27, pp. 3-6, 2003. DOI: 10.11532/proee2003.27.227 [ Links ]
[12] Shin, W., Miller, G.R., Arduino, P. and Mackenzie-Helnwein, P., Dynamic meshing for material point method computations, Eng. Technol., 48(9), pp. 84-92, 2010. [ Links ]
[13] Alonso, E.E., Pinyol, N.M. and Yerro, A., Mathematical modelling of slopes, Procedia Earth Planet. Sci., 9, pp. 64-73, 2014. [ Links ]
[14] Abe, K., Soga, K. and Bandara, S., Material point method for coupled hydromechanical problems, J. Geotech. Geoenviron. Eng., 1, pp. 1-16, 2013. DOI: 10.1061/(ASCE)GT.1943-5606.0001011 [ Links ]
[15] Bandara, S. and Soga, K., Coupling of soil deformation and pore fluid flow using material point method, Computers and Geotechnics, 63, pp. 199-214, 2015. DOI: 10.1016/j.compgeo.2014.09.009 [ Links ]
[16] Aristizabal-Giraldo, E.V., Informe técnico movimiento en masa barrio El Poblado, sector Cola del Zorro, AMVA, pp.1-3, 2008. [ Links ]
[17] Gómez, E.L. and Giraldo, V.M., Evaluación del deslizamiento en la Urbanización Alto Verde de la ciudad de Medellín, XV Jornadas Geotécnicas de la Ingeniería Colombiana, pp. 141-146, 2009. [ Links ]
[18] Buzzi, O., Pedroso, D.M. and Giacomini, A., Caveats on the implementation of the generalized material point method, Tech Sci. Press, 31(2), pp. 85-106, 2008. [ Links ]
[19] Nairn, J.A. and Guilkey, J.E., Axisymmetric form of the generalized interpolation material point method, Int. J. Numer. Methods Eng., vol. submited, pp. 1-25, 2014. DOI: 10.1002/nme.4792 [ Links ]
[20] Bardenhagen, S.G., Guilkey, J.E., Roessig, K.M., Brackbill, J.U., Witzel,W.M. and Foster, J.C., An improved contact algorithm for the material point method and application to stress propagation in granular material, Tech Sci. Press, 2(4), pp. 209-522, 2001. DOI: 10.3970/cmes.2001.002.509 [ Links ]
[21] Lemiale, V., Nairn, J. and Hurmane, A., Material point method simulation of equal channel angular pressing involving large plastic strain and contact through sharp corners, Tech Sci. Press, 70(1), pp. 41-66, 2010. DOI: 10.3970/cmes.2010.070.041 [ Links ]
[22] Nairn, J.A., Modeling imperfect interfaces in the material point method using multimaterial methods, Comput. Model. Eng. Sci., 1(1), pp. 1-15, 2013. [ Links ]
[23] Google, Google Earth 7.1.2.2041, [Online] 2013, [visitado en: 13/01/2015] [ Links ].
[24] Martínez- Arango, R., En la unidad residencial Alto Verde florece la esperanza, Periodico El Colombiano, publicado: 13/10/2013. [ Links ]
[25] Sawada, K., Moriguchi, S., Yashima, A., Zhang, F. and Uzuoka, R., Large deformation analysis in geomechanics using CIP method, JSME Int. J., 47(4), pp. 735-743, 2004. DOI: 10.1299/jsmeb.47.735 [ Links ]
[26] Nairn, J.A., Open-Source MPM and FEA Software - NairnMPM and NairnFEA. [Online]. [13/01/2015]. Disponible en: http://osupdocs.forestry.oregonstate.edu/index.php/Main_Page. [ Links ]
[27] Davies, T.R.H., Spreading of rock avalanche debris by mechanical fluidization, Rock Mech., 15, pp. 9-24, 1982. DOI: 10.1007/BF01239474 [ Links ]
[28] Davis, T., Geotechnical testing, observation, and documentation. Reston, American Society of Civil Engineers, 2008. [ Links ]
[29] Dai, F., Lee, C. and Ngai, Y.Y., Landslide risk assessment and management: an overview, Eng. Geol., 64(1), pp. 65-87, 2002. [ Links ]
[30] Uzielli, M., Nadim, F., Lacasse, S. and Kaynia, A.M., A conceptual framework for quantitative estimation of physical vulnerability to landslides, Eng. Geol., 102(3-4), pp. 251-256, 2008. DOI: 10.1016/j.enggeo.2008.03.011 [ Links ]
[31] Kaynia, A., Papathomakohle, M., Neuhauser, B., Ratzinger, K., Wenzel, H. and Medinacetina, Z., Probabilistic assessment of vulnerability to landslide: Application to the village of Lichtenstein, Baden-Württemberg, Germany, Eng. Geol., 101(1-2), pp. 33-48, 2008. DOI: 10.1016/j.enggeo.2008.03.008 [ Links ]
[32] Li, Z., Nadim, F., Huang, H., Uzielli, M. and Lacasse, S., Quantitative vulnerability estimation for scenario-based landslide hazards, Landslides, 7(2), pp. 125-134, 2010. DOI: 10.1007/s10346-009-0190-3 [ Links ]
[33] Uzielli, M., Catani, F., Tofani, V. and Casagli, N., Risk analysis for the Ancona landslide-II: Estimation of risk to buildings, Landslides, January, pp. 1-14, 2014. DOI: 10.1007/s10346-014-0477-x [ Links ]
[34] Li, Z., Nadim, F. Huang, H., Uzielli, M. and Lacasse, S., Quantitative vulnerability estimation for scenario-based landslide hazards, Landslides, 7(2) pp. 125-134, 2010. DOI: 10.1007/s10346-009-0190-3 [ Links ]
[35] Ragozin, A.L. and Tikhvinsky, I.O., Landslide hazard, vulnerability and risk assessment, Proceedings of the 8th International Symposium on Landslides, pp. 1257-1262, 2000. [ Links ]
[36] Muñoz, E., Martínez-Carvajal, H., Arévalo, J. and Alvira, D., Quantification of the effect of precipitation as a triggering factor for landslides on the surroundings of Medellín - Colombia, DYNA, 81(187), pp. 115-121, 2014. DOI: 10.15446/dyna.v81n187.40640 [ Links ]
M.A. Llano-Sena, es estudiante de doctorado en el Programa de Posgrado en Geotecnia de la Universidad de Brasilia, Brasil; actualmente se encuentra realizando una pasantía en la Universidad de Queensland, Australia. Trabaja problemas de grandes deformaciones en geotecnia como penetración y deslizamientos y sus aplicaciones usando el método del punto material (MPM). Maestro en Geotecnia formado en la Universidad de Brasília (2012). Ingeniero Civil graduado en la Facultad de Minas adscrita a la Universidad Nacional de Colombia, Sede Medellín (2010). ORCID: 0000-0002-4395-8636
M.M. Farias, recibió el título de Ingeniero Civil en 1983 en la Universidad Federal de Ceará, Brasil, el grado de MSc. en Geotecnia en 1986 por parte de la Pontificia Universidad de Rio de Janeiro, Brasil y su PhD en Métodos Numéricos en 1993 en la Universidad de Gales, Reino Unido. PhD. en 1998 formado en el Instituto Tecnológico de Nagoya -NIT, Japón. Es profesor de la Universidad de Brasilia desde 1986 e investigador del Consejo Nacional de Investigación (CNPq) del gobierno Brasileño. Sus principales áreas de acción se enmarcan en temas relacionados al modelamiento constitutivo y numérico aplicado a presas, túneles y diseño mecanístico de pavimentos. Link para información completa acerca del autor: http://lattes.cnpq.br/5345279954551868. ORCID: 0000-0002-5257-911X.
H.E. Martínez-Carvajal, se recibió de Ingeniero Geólogo en 1995 por la Universidad Nacional de Colombia, Medellín, Colombia; es MSc en Mecánica de Suelos, en 1999 de la Universidad Nacional Autónoma de México - UNAM, México y Dr. en Geotecnia, en 2006 en la Universidad de Brasilia, Brasil. Desde 1993 hasta 1999 trabajó para compañías consultoras en el área de Ingeniería Civil como geólogo de campo y exploración. Actualmente se desempeña como profesor asociado del Departamento de Ingeniería Civil y Ambiental en la Universidad de Brasilia, Brasil y Profesor de Cátedra en la Facultad de Minas de la Universidad Nacional de Colombia, Medellín, Colombia. Link para información completa acerca del autor: http://lattes.cnpq.br/2409917419986324. ORCID: 0000-0001-7966-1466.