Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.195 Medellín jan./fev. 2016
https://doi.org/10.15446/dyna.v83n195.47114
DOI: http://dx.doi.org/10.15446/dyna.v83n195.47114
Kinetic aspects of a dried thin layer carrot in a heat pump dryer
Aspectos cinéticos del secado de capa delgada de zanahoria en un secador de bomba de calor
Juan Carlos Gómez-Daza a & Claudia Isabel Ochoa-Martínez b
a Escuela de Ingeniería de Alimentos, Universidad del Valle, Cali, Colombia. juan.gomez.d@correounivalle.edu.co
b Escuela de Ingeniería de Alimentos, Universidad del Valle, Colombia, claudia.ochoa@correounivalle.edu.co
Received: November 6th, 2014. Received in revised form: August 20th, 2015. Accepted: December 18th, 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This article presents a mathematical model for drying thin layer carrot slices (Daucus carota) using a heat pump dryer (HPD). To select the equation that best describes the drying curve, 10 semi-theoretical and/or empirical models were evaluated. The parameters were determined using the Sigma-Plot® program, and their goodness of fit was compared using the correlation coefficient, R2; Chi-squared, c2; standard error of the estimate (SEE) and root mean square error (RMSE). Additionally, the effect of the relative moisture, sample thickness and air velocity on the effective diffusivity of the process was evaluated using a response surface tool. Although all the models correctly fit the experimental data, based on the statistical tests, the Wang-Singh model was selected as the best.
Keywords: drying; thin layer; modeling; diffusivity.
Resumen
Este artículo presenta un modelo matemático de capa delgada para secado de rodajas de zanahoria (Daucus carota) usando un secador de bomba de calor (HPD). Para seleccionar la mejor ecuación que describe la curva de secado, se evaluaron 10 modelos semi-teóricos y/o empíricos. Los parámetros se determinaron usando el programa Sigma-Plot® y la bondad de su ajuste se comparó usando el coeficiente de correlación R2; Chi-cuadrado, c2; error estándar del estimado (SEE) y raíz del error cuadrado medio (RMSE). Adicionalmente, se evaluó el efecto de la humedad relativa, el espesor de la muestra y la velocidad del aire sobre la difusividad efectiva del proceso usando la herramienta de superficie de respuesta. Aunque todos los modelos ajustaron correctamente los datos experimentales, se seleccionó el modelo de Wang-Singh como el mejor, basado en las pruebas estadísticas.
Palabras clave: secado; capa delgada; modelación; difusividad.
1. Introduction
Regarding the drying process, the term "thin-layer" applies to either a particle suspended freely in the drying air, or one layer of particle or a polylayer of many particles' thicknesses; the temperature and relative moisture of the drying air can be considered to be in the same thermodynamic state during the drying period [1]. Using this definition, any mathematical model for a particle also models the particles drying in a thin layer using any drying method, and the thin layer thickness may change with the velocity, temperature and relative moisture of the drying air.
The thickness of a thin layer increases if the drying air speed increases and when the thermodynamic state of the drying air reaches equilibrium with dry particles in the layer [1]. Due to the thin sample structure, a uniform temperature distribution can be assumed and may be modeled using lumped parameters [2].
The thin layer equations can be theoretical, semi-theoretical or empirical. The first only accounts for internal resistance to the moisture transfer between the product and air, while the others only consider external resistances to this moisture transfer. Theoretical models explain the product's behavior during drying and can be used for all process conditions despite including many assumptions that cause considerable error. The most widely used theoretical models are derived from Fick's second law of diffusion. Similarly, semi-theoretical models are generally derived from Fick's second law and modified to a simplified form. However, using experimental data requires making assumptions, and these theories are only valid within the applied process conditions. Empirical models have similar features to semi-theoretical models that strongly depend on the experimental conditions and provide limited information on the product behavior during drying [2]. The carrot is frequently used in studies of different preservation techniques due to its physical characteristics and available modeling and simulation data [3-12].
This article evaluates the experimental data fit for 10 thin layer models and explores the effect that relative moisture, sample thickness and air speed have on the kinetic behavior of dried carrot slices. The kinetic expression was established from analyzing the response surfaces and kinetic parameters controlling the heat pump drying process. Additionally, we determined the effective moisture diffusivity for each experiment and the activation energy of the processes.
2. Materials and methods
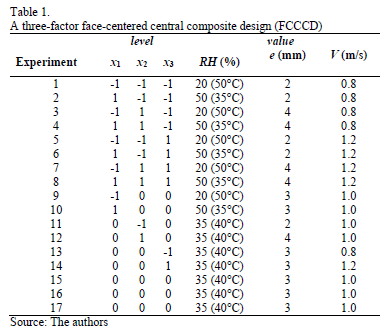
Nantes carrots (Daucus carota L.) were washed and cut into slices 3 cm in diameter and with a thickness of 2, 3 and 4 mm, according to the experimental design. The average initial moisture content of a fresh carrot was 0.8935 ± 0.024 (bh). The heat pump dryer (HPD) (Dártico brand) consisted of a cooling circuit containing a condenser, evaporator, compressor and expansion valve. The drying chamber contained 5 trays (0.36 × 0.36 m). The relative humidity (RH) and air velocity in the HPD were fixed. The drying temperature was directly linked to the RH (Table 1). A three-factor face-centered central composite design (FCCCD) was used with three repetitions at the central point, as shown in Table 1. The total weight (trays plus samples) was recorded for 5 hours with 2 min intervals for the first 10 minutes, 5 min intervals for half an hour, 10 min intervals for an hour and a half and 30 minute intervals for the last two hours.
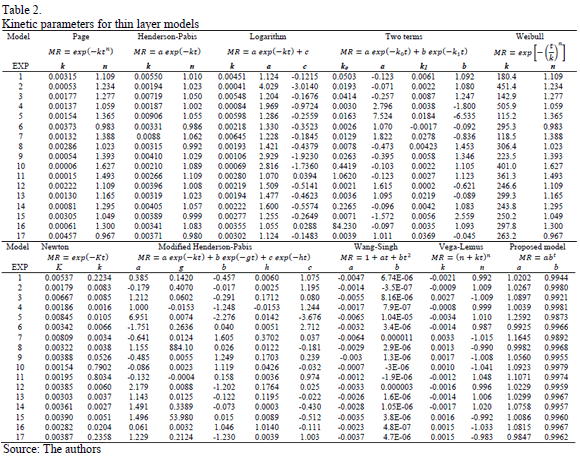
Table 2 shows the semi-theoretical models evaluated during the kinetic study [13]. The parameters for each model were estimated using Sigma-Plot® software. The moisture ratio (MR) value was determined according to the external conditions. If the relative humidity of the drying air is constant during the process, the equilibrium moisture content is also constant. The MR value was calculated using eq. (1).

where Mi is the initial moisture content (dry basis) obtained by drying in a vacuum oven at a constant weight and at 60ºC, Mt is the moisture content (dry basis) at time t based on the recorded weight, and Me is the equilibrium moisture content obtained from the carrot sorption isotherms (dry basis) [14, 15]: 0.055 [20% RH; 50 °C], 0.070 [35% RH; 40 °C] and 0.080 [50% RH; 35 °C].
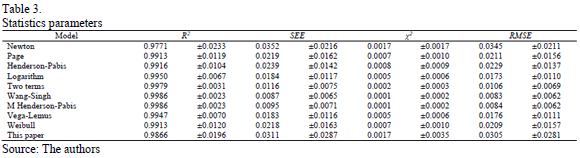
The model validities were checked using statistical parameters: correlation coefficient (R2), reduced Chi-squared test (c2), standard error of the estimate (SEE) and root mean square error (RMSE). The highest R2 and lowest c2, SEE and RMSE values determined the goodness of fit. The aforementioned criteria were calculated using eq. (2) - (5) [2,16].
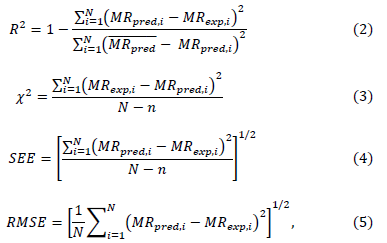
where N is the number of observations, n is the number of constants, MRpred,I is the ith predicted moisture ratio and MRexp,I is the ith experimental moisture ratio.
The Root Mean Squared Error has the advantage that it retains the units of the forecast variable and is thus more easily interpretable as a typical error magnitude. The Chi-squared Test is easy to implement (with multivariable data for example) [17] and also quite flexible..
The Henderson-Pabis model was rearranged to determine the diffusivity coefficient based on eq. (6) [2]:

where a is a shape index and, k is the drying constant defined by eq. (7):

where A2 is a geometric constant (4e2 for infinite slices), and e is half the slice thickness if drying occurs on both sides and the full thickness if drying occurs on only one side. Eq. (6) indicates ln(MR) varies linearly with t and the slope is equal to k.
Eq. (8) was used to calculate the activation energy (Ea):
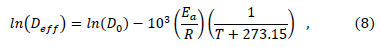
where D0 (m2/s) is the Arrhenius factor that is generally defined as the reference diffusion coefficient at an infinitely high temperature, Ea (kJ/mol) is the diffusion activation energy, and R (kJ/kmolK) is the universal gas constant. Eq. (8) is linear and allows Ea to be calculated from the slope.
3. Results and discussion
Table 2 shows the parameters for each model that fit the experimental data and Table 3 shows the fit for each model using the statistical parameters from each experiment. In general, all models had high correlation coefficients and low values for the other statistics. The Wang-Singh and modified Henderson-Pabis models exhibited the best values; however, the Wang-Singh model has fewer adjustable parameters. A statistical discrimination study based on nonlinear regression ensures the Wang-Singh equation best fits the data [18].
Thin layer equations may be theoretical, semi-theoretical, and empirical models. Semi-theoretical models are generally derived from Fick's second law of diffusion and are modifications of its simplified forms [2].
Empirical models used are: The Lewis (Newton) model, which is analogous with Newton's law of cooling. The Page model modifies the Newton model to get a more accurate model by adding a dimensionless empirical constant (n) [2].
The models derived from Fick's second law of diffusion are: the Henderson-Pabis model, and the Logarithmic model, which is formed by adding an empirical term. The Two-Term model uses the first two terms of the general series solution of Fick's second law of diffusion to correct the shortcomings of the Henderson-Pabis model. The Modified Henderson-Pabis model improves previous models by adding the third term of the general solution from Fick's second law of diffusion [2].
The Weibull, Wang-Singh, Vega-Lemus and Proposed models, are all empirical models.
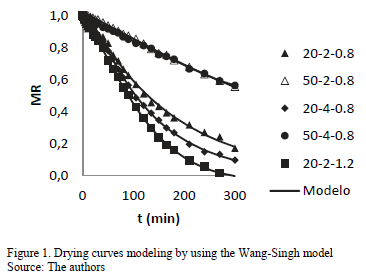
Fig. 1 shows the drying curves and their fit to the Wang-Singh model for 5 of the 17 experiments. The first number in the code corresponds to the relative humidity (20 and 50%), the second is the thickness (2 and 4 mm), and the last is the air velocity (0.8 and 1.2 m/s).
The relative humidity and air velocity affect the drying time; a lower relative humidity and higher velocity provide faster drying times regardless of the sample thickness. Krokida [3] found temperature to be the most important factor in the drying rate, while the velocity and humidity have lesser effects. In that study, the evaluated temperatures were higher (65, 75 and 85 °C).
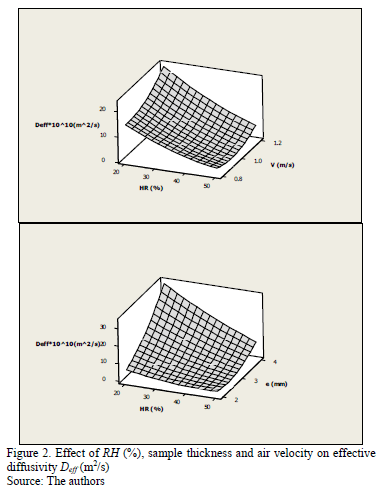
The effective diffusivity (Deff) was determined using eq. (6) - (7) and the least squares analysis for each experiment. Fig. 2 shows the response surfaces for the effective diffusivity, Deff. Larger effective diffusivities were obtained at lower relative humidities, higher material thicknesses and high air velocities. The desirability function confirms these results. The Deff values were between 2.01E-10 and 4.38E-9 m2/s. Doymaz [19] determined the effective diffusivity values for the convective drying of carrots ranged from 7.76E-10 to 9.34E-10 m2/s and argues that this variable increases when air flow and temperature are increased ; these are similar to this study's observations (Fig. 2), which account for the decreased RH at an increased temperature (Table 1). Kaya et al. [14] also found that decreasing the RH (temperature increase for a closed system) increased the effective diffusivity values. However, Phoungchandang et al. [20] determined that the effective diffusivity values ranged from 8.34E-11 to 2.77E-10 m2/s for dried carrots in a heat pump dryer at 40, 50 and 60 °C with an air velocity of 0.5 m/s. Panagiotou et al. [21] reported Deffvalues (m2/s) ranging from 2.20E-12 to 7.46E-9 for moisture contents between 0.10 and 15.0 on a dry basis and temperatures between 20 and 100 °C. Torres et al. [22] also obtained similar results working with yam in a convective drier.
The p value obtained from the ANOVA for the effective diffusivity, Deff, was less than 0.05 for the regression term. This means that there is a statistically significant relationship between the variables on a 95% confidence level, specifically between the quadratic and interaction terms. The linear terms can be omitted from the model because they would have no significance at this confidence level. This is corroborated by the p-values for the regression coefficients in which only the second order term (RH * e) was significant and is effectively an interaction. The p value is the specific probability that the observed value of the test statistic, together with all other possible values of the test statistic that are at least as unfavorable as the null hypothesis, will occur [17].
Validation of the model via a residual analysis only happens when the probability curve that shows normal error behavior is observed. Residuals are not far from the line; the variance is homogeneous, and the largest deviation occurred in experiment 9.
The activation energy obtained was 35.50 kJ/mol, and the literature reports activation energies for carrot drying using different equipment and different processing conditions.
According to the energy levels involved and collision theory for reactive molecules, enough energy must be generated to provide the required activation energy and facilitate the reaction. The activation energy itself does not provide information on the reactivity of a given system, only on the temperature dependence of the reaction. Activation Energy activation is also related to the moisture content. The diffusion activation energy increased at lower moisture contents because the interaction between the moisture and solid is generally stronger at lower moisture contents [23].
4. Conclusions
All of the thin layer models evaluated could fit the experimental data. The Wang-Singh model exhibited the best fit for the experimental data, based on the criteria of having the highest correlation coefficient (R2) and lowest Chi-squared statistic (c2), standard error of the estimate (SEE) and root mean square error (RMSE) values. A significant effect from the HR*e interaction was found during the ANOVA for effective diffusivity. The conditions that provide the best evaluated parameters (low MR and high Deff) are: 20% HR, 4 mm thickness and 1.2 m/s air velocity.
References
[1] Ayas, D.S., Cenkowski, S., Pabis, S. and Muir, W.E., Review of thin-layer drying and wetting equations. Drying Technology, 9(3), pp. 551-588, 1991. [ Links ]
[2] Erbay, Z. and Icier, F., A review of thin layer drying of foods: Theory, modeling, and experimental results. Critical Review in Food Science and Nutrition, 50(5), pp. 441-464, 2010. DOI: 10.1080/10408390802437063 [ Links ]
[3] Krokida, M.K., Karathanos, V.T., Maroulis, Z.B. and Marinos-Kouris, D., Drying kinetics of some vegetables. Journal of Food Engineering, 59, pp. 391-403, 2003. DOI: 10.1016/S0260-8774(02)00498-3 [ Links ]
[4] Srikiatden, J. and Roberts, J.S., Measuring moisture diffusivity of potato and carrot (core and cortex) during convective hot air and isothermal drying. Journal of Food Engineering, 74(1), pp. 143-152, 2006. DOI: 10.1016/j.jfoodeng.2005.02.026 [ Links ]
[5] Togrul, H., Suitable drying model for infrared drying of carrot. Journal of Food Engineering, 77(3), pp. 610-619, 2006. DOI: 10.1016/j.jfoodeng.2005.07.020 [ Links ]
[6] Erenturk, S. and Erenturk, K., Comparison of genetic algorithm and neural network approaches for the drying process of carrot. Journal of Food Engineering, 78(3), pp. 905-912, 2007. DOI: 10.1016/j.jfoodeng.2005.11.031 [ Links ]
[7] Singh, B. and Gupta, A.K., Mass transfer kinetics and determination of effective diffusivity during convective dehydration of pre-osmosed carrot cubes. Journal of Food Engineering, 79(2), pp. 459-470, 2007. DOI: 10.1016/j.jfoodeng.2006.01.073 [ Links ]
[8] Mihoubi, D., Timoumi, S. and Zagrouba, F., Modelling of convective drying of carrot slices with IR heat source. Chemical Engineering and Processing: Process Intensification, 48(3), pp. 808-815, 2009. DOI: 10.1016/j.cep.2008.10.004 [ Links ]
[9] Phongsomboon, P. and Intipunya, P., Comparative study on drying of osmotic treated carrot slices. Asian Journal of Food and Agro-Industry, 2(04), pp. 448-456, 2009. [ Links ]
[10] Hiranvarachat, B., Devahastin, S. and Chiewchan, N., Effects of acid pretreatments on some physicochemical properties of carrot undergoing hot air drying. Food and Bioproducts Processing, 89(2), pp. 116-127, 2011. DOI: 10.1016/j.fbp.2010.03.010 [ Links ]
[11] Zielinska, M. and Markowski, M., Air drying characteristics and moisture diffusivity of carrot. Chemical Engineering and Processing: Process Intensification, 49(2), pp. 212-218, 2010. DOI: 10.1016/j.cep.2009.12.005 [ Links ]
[12] Nazghelichi, T., Kianmehr, M.H. and Aghbashlo, M., Thermodynamic analysis of fluidized bed drying of carrot cubes. Energy, 35(12), pp. 4679-4684, 2010. DOI: 10.1016/j.energy.2010.09.036 [ Links ]
[13] Xanthopoulos, G., Oikonomou, N. and Lambrinos, G., Applicability of a single-layer drying model to predict the drying rate of whole figs. Journal of Food Engineering, 81(3), pp. 553-559, 2007. DOI: 10.1016/j.jfoodeng.2006.11.033 [ Links ]
[14] Kaya, A., Aydin, O. and Demirtas, C., Experimental and theoretical analysis of drying carrots. Desalination, 237(1-3), pp. 285-295, 2009. DOI: 10.1016/j.desal.2008.01.022 [ Links ]
[15] Eim, V.S., Roselló, C., Femenia, A. and Simal, S., Moisture sorption isotherms and thermodynamic properties of carrot. International Journal of Food Engineering, 7(3), Article 13, pp. 1-16, 2011. DOI: 10.2202/1556-3758.1804 [ Links ]
[16] Vega-Gálvez, A., Andrés, A., Gonzalez, E., Notte-Cuello, E., Chacana, M. and Lemus-Moncada, R., Mathematical modeling on the drying process of yellow squat lobster (Cervimunida jhoni) fishery waste for animal feed. Animal Feed Science and Technology, 151(3-4), pp. 268-279, 2009. DOI: 10.1016/j.anifeedsci.2009.01.003 [ Links ]
[17] Wilks, D.S., Statistical methods in the atmospheric sciences. Second Edition. Amsterdam: Academic Press, 2006. [ Links ]
[18] Barrozo, M.A.S., Sartori, D.J.M. and Freire, J.T., A study of the statistical discrimination of the drying kinetics equations. Food and Bioproducts Processing, 82(C3), pp. 219-225, 2004. DOI: 10.1205/fbio.82.3.219.44176 [ Links ]
[19] Doymaz, I., Convective air drying characteristics of thin layer carrots. Journal of Food Engineering, 61(3), pp. 359-364, 2004. DOI: 10.1016/S0260-8774(03)00142-0 [ Links ]
[20] Phoungchandang, S. and Wongwatanyoo, J., Desorption isotherms and drying characteristics of carrot using tray and heat pump-assisted dehumidified drying. KKU Research Journal, 15(3), pp. 171-186, 2010. [ Links ]
[21] Panagiotou, N.M., Krokida, M.K., Maroulis, Z.B. and Saravacos, G.D., Moisture diffusivity: Literature data compilation for foodstuffs. International Journal of Food Properties, 7(2), pp. 273-299, 2004. DOI: 10.1081/JFP-120030038 [ Links ]
[22] Torres, R., Montes, E.J., Andrade, R.D., Perez, O.A. and Toscano, H., Drying kinetics of two yam (Dioscorea alata) varieties. DYNA, 79(171), pp. 175-182, 2012. [ Links ]
[23] Kahveci, K. and Cihan, A., Drying of food materials: Transport Phenomena. New York: Nova Science Publishers, Inc., 2008. [ Links ]
J.C. Gómez-Daza, received his BSc. in Chemical Engineering in 1996, his MSc. in Chemical Engineering in 1999, and his PhD in Engineering in 2014, all from the Universidad del Valle, Cali, Colombia. From 1987 to 1991, he worked for the Industria de Licores del Valle and Lloreda Grasas and since 2000 he has worked at the Universidad del Valle. Currently, he is a full professor in the Food Engineering School, Facultad de Ingeniería, at the Universidad del Valle. He works as an occasional lecturer at the Universidad Nacional de Colombia, in Palmira, in the areas of process dynamic physicochemical and biological, mathematical and numeric methods and drying. His research interests include: modeling, simulation and drying; process engineering; process dynamics. ORCID: 0000-0001-7464-0519
C.I. Ochoa-Martínez, received his BSc. Chemical Engineering in 1989, his MSc. in Chemical Engineering in 2001, and his PhD in Engineering in 2006. She has worked in programs and projects in the food area since 2006 at the Universidad del Valle. She is currently a full professor in the Food Engineering School, Facultad de Ingeniería, Universidad del Valle. Her research interests include: modeling, simulation and drying; process engineering. She has several publications in scientific journals and is currently coordinator of the post-graduate program at the Food Engineering School. ORCID:0000-0002-2666-1726