Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.195 Medellín jan./fev. 2016
https://doi.org/10.15446/dyna.v83n195.47873
DOI: http://dx.doi.org/10.15446/dyna.v83n195.47873
Sparse representations of dynamic scenes for compressive spectral video sensing
Representaciones dispersas de escenas dinámicas y reconstrucciones a partir de muestreo compresivo
Claudia V. Correa-Pugliese a, Diana F. Galvis-Carreño b & Henry Arguello-Fuentes c
a Department of Electrical and Computer Engineering, University of Delaware, Newark, DE, USA. clavicop@udel.edu
b Escuela de Ingeniería Química, Universidad Industrial de Santander, Bucaramanga, Colombia. diana.galvis1@correo.uis.edu.co
c Escuela de Ingeniería de Sistemas, Universidad Industrial de Santander, Bucaramanga, Colombia. henarfu@uis.edu.co
Received: December 12th, 2014. Received in revised form: July 29th, 2015. Accepted: August 19th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The coded aperture snapshot spectral imager (CASSI) is an optical architecture that captures spectral images using compressive sensing. This system improves the sensing speed and reduces the large amount of collected data given by conventional spectral imaging systems. In several applications, it is necessary to analyze changes that occur between short periods of time. This paper first presents a sparsity analysis for spectral video signals, to obtain accurate approximations and better comply compressed sensing theory. The use of the CASSI system in compressive spectral video sensing then is proposed. The main goal of this approach is to capture the spatio-spectral information of dynamic scenes using a 2-dimensional set of projections. This application involves the use of a digital micro-mirror device that implements the traditional coded apertures used by CASSI. Simulations show that accurate reconstructions along the spatial, spectral and temporal axes are attained, with PSNR values of around 30 dB.
Keywords: spectral dynamic scenes, compressive spectral imaging, sparse representations, coded apertures, CASSI.
Resumen
El sistema de adquisición de imágenes espectrales de apertura codificada (CASSI) es una arquitectura óptica que capta imágenes espectrales usando muestreo compresivo. Este sistema acelera la detección y reduce la gran cantidad de datos adquiridos por los sistemas tradicionales. En algunas aplicaciones es necesario analizar la variabilidad de la escena en períodos cortos de tiempo. Este trabajo presenta un análisis de las bases de representación para imágenes espectrales dinámicas, con el fin de obtener aproximaciones correctas a partir de su representación dispersa, y permitir la aplicación de muestreo compresivo. Posteriormente se propone el uso del sistema CASSI captar la información espacial y espectral de escenas dinámicas utilizando un conjunto de proyecciones bidimensionales. Esto implica el uso de un dispositivo de microespejos digitales que implementa las aperturas codificadas utilizadas en CASSI. Resultados muestran que es posible obtener reconstrucciones correctas en las dimensiones espaciales, espectral y temporal, con valores de PSNR alrededor de 30 dB.
Palabras clave: imágenes espectrales dinámicas, muestreo compresivo de imágenes multi-espectrales, representaciones dispersas, aperturas codificadas, CASSI.
1. Introduction
Traditional imaging architectures capture light intensity values on each spatial location and compression techniques are then used for data storage and transmission [1]. In contrast, spectral imaging provides light intensity values across a range of wavelengths. Thus, each spatial point of a spectral image provides a complete spectral signature of the composition of a scene. Conventional spectral imaging systems rely on Nyquist criterion to acquire the spatio-spectral information of an object or scene. These systems experience an extremely low sensing speed and, need to store large amounts of collected data, proportional to the desired resolution [2]. An alternative approach for spectral imaging acquisition, known as Compressive Spectral Imaging (CSI), has recently emerged. CSI applies compressed sensing (CS) principles to capture and recover the spatial and spectral information of a scene in a single two-dimensional set of projections. In particular, CSI assumes that a spectral image 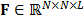 , has a sparse representation in a basis
, has a sparse representation in a basis  , such that it can be recovered from
, such that it can be recovered from 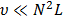 random projections [3]. Therefore, the selection of the sparse basis
random projections [3]. Therefore, the selection of the sparse basis  is critical to obtain good reconstruction results [4].
is critical to obtain good reconstruction results [4].
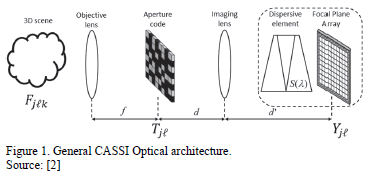
The coded aperture snapshot spectral imager (CASSI) shown in Fig. 1 is an optical architecture designed to capture CSI measurements [3,5]. The CASSI architecture comprises a set of lenses, a coded aperture, a dispersive element (commonly a prism), and a focal plane array (FPA) detector. Several variations of the CASSI system have been proposed to improve the quality of the obtained images. For instance, multiple shots can be attained by varying the coded aperture patterns, thus, more information about the scene is extracted [6-8]; an optimal coded aperture design for spectral selectivity has been proposed in [3]; a high resolution coded aperture and a low resolution FPA are used to obtain spatial super resolution in the CASSI system without incurring on expensive detectors [9]. Furthermore, spectral super resolution is attained by adding a second coded aperture [10]. Finally, traditional block-unblock coded apertures have recently been replaced by an array of optical filters [11].
In many applications such as surveillance, or some microscopic biological studies, the scenes under analysis are not completely static; conversely, many changes may occur between short periods of time. Thus, not only the spatial and spectral, but also temporal information is of high interest. For instance, hyperspectral video is used for object or human tracking [12-15], for cancer detection through endoscopy [16], bile duct inspection [17] and several types of surgery [18,19]. The acquisition of this four-dimensional information from a scene is known as spectral video sensing. Furthermore, when CS techniques are used to sense these video signals, it is known as compressive spectral video sensing. Previous works have proposed different video spectral acquisition approaches. For instance, in [20] different sets of spectral bands are measured on each video frame, and then a sparsity assumption is used to reconstruct the data. Since each frame does not contain information from all the spectral bands, this approach is not capable of capturing the variations that may occur on the spectral bands during the acquisition time. Other spectral video sensing approaches include multiple sensors to capture several video streams that are processed to obtain a single high-resolution signal [21], or dispersive elements in conjunction with occlusion masks to capture spectral information in a monochrome camera [22,23]. These approaches, however, do not employ CS theory. Moreover, an architecture named coded aperture compressive temporal imaging (CACTI) captures a single coded measurement by shifting a large coded aperture [24]; this coded measurement is then used to estimate several video frames, but no spectral information is taken into account. Similar spectral video sensing approaches can be found in [25-27]. CS concepts have been recently exploited in spectral video sensing, in particular, a recent variation of CACTI is the coded aperture compressive spectral-temporal imaging (CACSTI) [28, 29], which employs mechanical translation of a coded aperture and spectral dispersion to capture a multi-spectral dynamic scene onto a monochrome detector. Capturing information from all frames in a single snapshot however, leads to an extremely ill-posed reconstruction problem.
This paper presents a sparsity analysis of spectral video signals. These sparse representations can be exploited by using the CASSI system to capture the spatio-spectral information of dynamic scenes. In particular, this approach implements the coded aperture patterns using a digital micro-mirror device (DMD) that switches the patterns to independently encode the information from different frames. More specifically, the compressive spectral video problem can be expressed in the following ways: the input source is a four-dimensional array with two spatial, one spectral and, one temporal dimension. The physical phenomenon is mathematically described in the following way: the  th spectral video frame of the input source,
th spectral video frame of the input source, 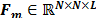 , is first spatially modulated by the coded aperture
, is first spatially modulated by the coded aperture 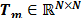 , where
, where 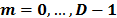 indexes the temporal dimension; thus, a coded aperture pattern remains fixed to capture the information from each frame. Then, the dispersive element decomposes the encoded source frame into its spectral components. Finally, the encoded spatio-spectral information from a specific frame is integrated across the spectral components into the FPA, such that multiplexed spatio-spectral information is captured on each pixel. The output of the system for the
indexes the temporal dimension; thus, a coded aperture pattern remains fixed to capture the information from each frame. Then, the dispersive element decomposes the encoded source frame into its spectral components. Finally, the encoded spatio-spectral information from a specific frame is integrated across the spectral components into the FPA, such that multiplexed spatio-spectral information is captured on each pixel. The output of the system for the 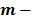 th frame can be modeled as
th frame can be modeled as 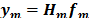 , where
, where 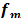 is the vector form the video frame
is the vector form the video frame 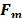 and,
and, 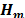 is the transfer function of the system that contains the effects of the coded aperture
is the transfer function of the system that contains the effects of the coded aperture 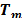 and the prism. This procedure is repeated to capture information from a scene in different frames of time.
and the prism. This procedure is repeated to capture information from a scene in different frames of time.
A variation of the CASSI system allows multiple snapshot acquisition of a spectral scene [2,6,8,30]. This modification results in better reconstruction quality. Using this multiple-shot scheme, several measurement sets are captured for each frame in the spectral video, using different coded aperture patterns. Different patterns can be implemented using DMD [7] or piezo-electric devices [8]. Thus, the measurements from 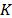 snapshots and
snapshots and 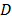 frames can be arranged as
frames can be arranged as 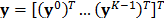 , where
, where 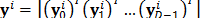 , such that the sensing model can be rewritten as
, such that the sensing model can be rewritten as 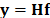 , where
, where 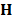 is the sensing matrix that contains all
is the sensing matrix that contains all 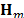 's and
's and 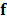 is the vector representation of the complete video data set
is the vector representation of the complete video data set 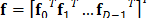 . In practice, the maximum number of measurements directly depends on both the pattern rate of the DMD and, the integration time of the detector. Most commercial DMDs have pattern rates of around 30 KHz, yet most CCD detectors can integrate 30 frames-per-second. In other words, a high-speed detector is a critical device in these kinds of applications.
. In practice, the maximum number of measurements directly depends on both the pattern rate of the DMD and, the integration time of the detector. Most commercial DMDs have pattern rates of around 30 KHz, yet most CCD detectors can integrate 30 frames-per-second. In other words, a high-speed detector is a critical device in these kinds of applications.
The set of projections captured in the FPA, 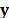 , is then used to recover the four-dimensional (spatio-spectral-temporal) input scene. The reconstruction is performed by solving an optimization problem that finds a sparse representation of the original data in a given basis. Commonly, the reconstruction problem is expressed as
, is then used to recover the four-dimensional (spatio-spectral-temporal) input scene. The reconstruction is performed by solving an optimization problem that finds a sparse representation of the original data in a given basis. Commonly, the reconstruction problem is expressed as 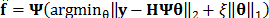 , where
, where 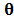 is a sparse representation of
is a sparse representation of 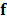 in the basis
in the basis 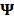 , and
, and 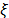 is a regularization constant.
is a regularization constant.
This paper contains two major contributions; first, a sparsity analysis is developed in order to determine the basis that provides the sparsest representation of spectral video signals. Then, we present a mathematical model for the multi-shot CASSI system that can capture dynamic scenes using a two-dimensional set of projections. This paper is organized as follows: first, an introduction of sparse representation for dynamic scenes is presented; then, the mathematical model for compressive spectral imaging of spectral dynamic scenes is shown; finally, simulations and results to test this approach are included in section 4.
2. Sparse representation of spectral video signals
Compressed sensing exploits the fact that many signals are naturally sparse, or have a sparse representation on a given basis. In other words, this concept establishes that most of the energy from a signal is concentrated in either a small portion of its elements or its coefficients on a representation basis. Let 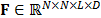 be a spectral video with
be a spectral video with 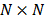 pixels of spatial resolution,
pixels of spatial resolution, 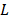 spectral bands and
spectral bands and 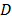 video frames. The vector form of
video frames. The vector form of 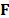 ,
, 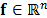 with
with 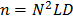 , can be represented on the basis
, can be represented on the basis 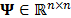 as
as
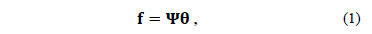
where 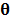 is a sparse vector of coefficients.
is a sparse vector of coefficients.
In particular, CSI also relies on the sparsity nature of the data. Commonly, one representation basis is used for each dimension of a spectral image. Thus, four representation bases are used for spectral video signals, 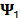 and
and 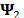 for the spatial axes,
for the spatial axes, 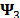 for the spectral axis and,
for the spectral axis and, 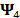 for the temporal coordinate. In general, if one frame of a video spectral signal is a common spectral image data cube, then it can be expressed as
for the temporal coordinate. In general, if one frame of a video spectral signal is a common spectral image data cube, then it can be expressed as 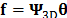 , where
, where 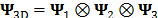 and,
and, 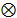 denotes the kronecker product. Usually in spectral images, a 2D Wavelet transformation is used for the spatial dimensions
denotes the kronecker product. Usually in spectral images, a 2D Wavelet transformation is used for the spatial dimensions 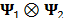 and, the Discrete Cosine Transform (DCT) is used for the spectral dimension,
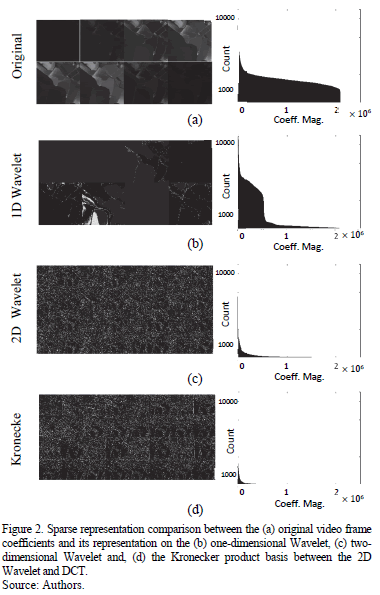
and, the Discrete Cosine Transform (DCT) is used for the spectral dimension, 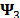 . Fig. 2 shows the sparse representation of one frame from a spectral video using three different Kronecker product bases. Fig. 2 (a) shows the
. Fig. 2 shows the sparse representation of one frame from a spectral video using three different Kronecker product bases. Fig. 2 (a) shows the 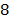 original spectral bands of the single frame, Fig. 2 (b) presents the spectral frame representation using a 1-dimensional Wavelet transformation, Fig. 2 (c) shows the frame representation in a 2-dimensional Wavelet basis and, Fig. 2 (d) shows the spectral frame representation in a three-dimensional basis obtained from the Kronecker product between a 2D Wavelet Symmlet 8 and a DCT bases. It can be noticed in Fig. 2 that the Kronecker product basis provides a sparser representation of the spectral frame. Thus, most of the energy from the signal is concentrated in fewer coefficients
original spectral bands of the single frame, Fig. 2 (b) presents the spectral frame representation using a 1-dimensional Wavelet transformation, Fig. 2 (c) shows the frame representation in a 2-dimensional Wavelet basis and, Fig. 2 (d) shows the spectral frame representation in a three-dimensional basis obtained from the Kronecker product between a 2D Wavelet Symmlet 8 and a DCT bases. It can be noticed in Fig. 2 that the Kronecker product basis provides a sparser representation of the spectral frame. Thus, most of the energy from the signal is concentrated in fewer coefficients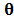 .
.
The effect of the different bases is illustrated in Fig. 3, where different approximations of one spectral frame are obtained by retaining only 1% of the sparse representation coefficients in a Wavelet 1D, Wavelet 2D and a Kronecker product bases. These approximations are obtained by expressing the signal in the corresponding representation bases, then the coefficients are sorted according to their magnitude and the smallest coefficients of the video frame in each basis are set to zero, while the 1% largest elements are preserved. A reconstruction is then obtained by applying the correspondent inverse transformation represented as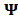 . It can be noticed in Fig. 3 that the approximation images show a great similarity with the original, especially when the Kronecker product basis is employed.
. It can be noticed in Fig. 3 that the approximation images show a great similarity with the original, especially when the Kronecker product basis is employed.
Previous works analyze the sparse representation of a single frame from a spectral video that can be seen as a static spectral image and, can be modeled using a three-dimensional basis, 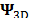 . However, appropriate sparse representations of the whole dynamic spectral scenes have not been yet considered in the literature. It has been previously shown that the three-dimensional basis provides the sparsest representation of the three-dimensional structure of a spectral image. Similarly, a four-dimensional basis (
. However, appropriate sparse representations of the whole dynamic spectral scenes have not been yet considered in the literature. It has been previously shown that the three-dimensional basis provides the sparsest representation of the three-dimensional structure of a spectral image. Similarly, a four-dimensional basis (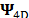 ) exploits the sparsity of a dynamic spectral image, given that a single transformation is assumed for each coordinate of the signal. Thus, a dynamic spectral (four-dimensional) video can be mathematically represented as
) exploits the sparsity of a dynamic spectral image, given that a single transformation is assumed for each coordinate of the signal. Thus, a dynamic spectral (four-dimensional) video can be mathematically represented as
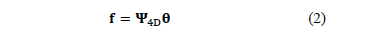
where 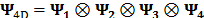 and,
and, 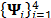 is a set of different 1-dimensional transformations. An analysis of the representation bases applied to spectral video signals is presented in Section 4.
is a set of different 1-dimensional transformations. An analysis of the representation bases applied to spectral video signals is presented in Section 4.
3. Compressive spectral imaging for spectral dynamic scenes
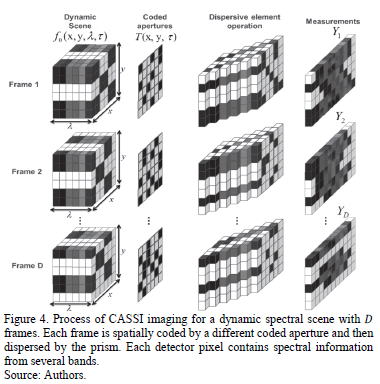
Compressive spectral imaging theory has previously been used to acquire spatial and spectral information of a scene. These previous optical architectures can be extended to the acquisition of dynamic spectral scenes, by exploiting the sparse basis discussed in the preceding section. In particular, the CASSI architecture presented in Fig. 1 can be employed to sense video spectral information. Fig. 4 shows the sensing process for a dynamic spectral scene.
Several measurement shots are usually captured in CSI, such that the captured projections extract most of the details in the scene, and thus the obtained reconstruction is more accurate. Furthermore, increasing the number of captured projections during a particular frame leads to a less ill-posed inverse problem. In particular, each additional measurement shot uses a different coded aperture for each frame, which remains fixed during the integration time of the detector. First, the mathematical model for a single shot is presented, and then a model for the multiple shot scheme is developed.
3.1. Single snapshot mathematical model
Let 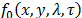 be a dynamic spectral source, where
be a dynamic spectral source, where 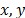 index the spatial axes,
index the spatial axes, 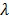 is the index for the spectral dimension, and
is the index for the spectral dimension, and 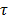 is the temporal/frame index. Each frame from the source is first spatially modulated by a time-dependent coded aperture
is the temporal/frame index. Each frame from the source is first spatially modulated by a time-dependent coded aperture 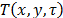 . This coded aperture remains fixed for each frame during the integration time of each measurement shot. In other words, every frame from the scene is modulated by a different pattern in the coded aperture.
. This coded aperture remains fixed for each frame during the integration time of each measurement shot. In other words, every frame from the scene is modulated by a different pattern in the coded aperture.
Then, the coded field correspondent to each frame is dispersed by a prism yielding 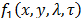 , as expressed in eq. (3)
, as expressed in eq. (3)
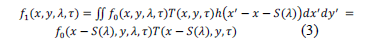
where 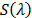 represents the dispersion function of the prism and,
represents the dispersion function of the prism and, 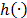 is the impulse response of the system. The output for the
is the impulse response of the system. The output for the 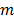 -th frame,
-th frame, 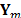 is obtained by integrating the field
is obtained by integrating the field 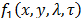 over the spectral range sensitivity of the camera,
over the spectral range sensitivity of the camera, 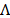 , during the interval time
, during the interval time 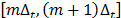 , where
, where 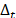 is the integration time of the detector. Thus, the resulting field
is the integration time of the detector. Thus, the resulting field 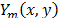 can be expressed as
can be expressed as
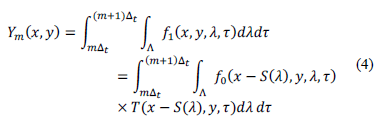
for 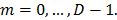
Since the detector is a pixelated array, the energy from the 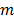 -th frame that is captured in the
-th frame that is captured in the 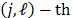 pixel can be expressed as
pixel can be expressed as
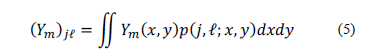
where 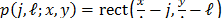 represents the rectangular pixel, with pixel size
represents the rectangular pixel, with pixel size 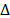 . Similarly, the
. Similarly, the 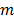 -th coded aperture can be also discretized as
-th coded aperture can be also discretized as
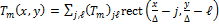 and the discrete source can be represented as
and the discrete source can be represented as
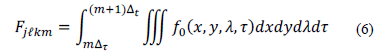
where 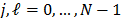 , index the spatial coordinates,
, index the spatial coordinates, 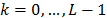 , indexes the spectral components,
, indexes the spectral components, 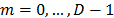 , indexes the frames. This discretization yields a 4-dimensional representation of the dynamic scene,
, indexes the frames. This discretization yields a 4-dimensional representation of the dynamic scene, 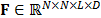 , where
, where 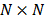 are the spatial dimensions,
are the spatial dimensions, 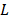 is the number of spectral bands and,
is the number of spectral bands and, 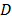 is the number of frames. Using these discrete representations, the energy captured on the detector, that comes from the
is the number of frames. Using these discrete representations, the energy captured on the detector, that comes from the 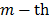 frame, can be written as
frame, can be written as
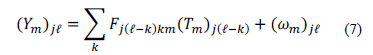
where the dispersion effect is represented by the shifting in the 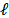 -axis and,
-axis and, 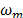 is the noise in the system.
is the noise in the system.
The measurement set acquired from a single frame, 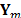 , can be represented in vector form as
, can be represented in vector form as 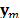 . Similarly, the spatio-spectral source
. Similarly, the spatio-spectral source 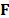 can be expressed in vector form as
can be expressed in vector form as 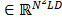 , and the relation between the
, and the relation between the 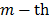 source frame and its correspondent measurement set is given by
source frame and its correspondent measurement set is given by
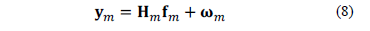
where 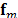 is the vector representation of the
is the vector representation of the 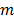 -th frame and,
-th frame and, 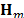 is the single-shot CASSI sensing matrix that accounts for the effects of the coded aperture pattern
is the single-shot CASSI sensing matrix that accounts for the effects of the coded aperture pattern 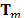 and the dispersive element. Furthermore, measurements acquired from different frames can also be arranged in a single vector,
and the dispersive element. Furthermore, measurements acquired from different frames can also be arranged in a single vector, 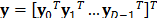 , where
, where 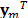 is the vector representation of the measurement corresponding to the
is the vector representation of the measurement corresponding to the 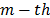 frame. Thus, the system can be modeled in matrix form as follows
frame. Thus, the system can be modeled in matrix form as follows
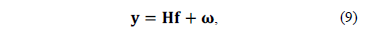
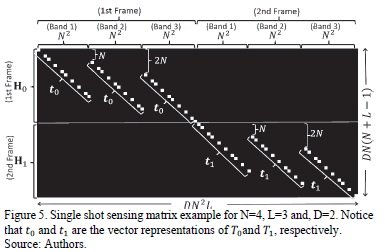
where 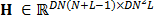 is the single-shot sensing matrix for the complete dynamic scene. This matrix groups the matrices for all frames as the matrix given by
is the single-shot sensing matrix for the complete dynamic scene. This matrix groups the matrices for all frames as the matrix given by 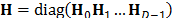 . Fig. 5 shows an example of the structure of the sensing matrix
. Fig. 5 shows an example of the structure of the sensing matrix 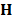 , in which the white points correspond to the non-zero elements of the matrices
, in which the white points correspond to the non-zero elements of the matrices 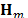 and, are determined by the coded aperture patterns used for each frame.
and, are determined by the coded aperture patterns used for each frame.
3.2. Multiple snapshot mathematical model
In general, a single snapshot in CASSI allows the underlying data cube to be reconstructed. However, multiple snapshots using different coded aperture patterns yield a less ill-posed inverse problem, and better quality reconstructions.
Similarly, several measurement shots can be captured for each single source frame. To this end, the duration of the frame is seen as a set of smaller time intervals, in which the coded aperture pattern is shuffled and, the detector captures a new set of compressive measurements each time. Thus, each measurement shot has duration of 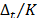 time units, and
time units, and 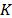 measurement shots are captured for each frame. Fig. 6 presents a timeline that illustrates this concept. It can be noticed that a detector with integration time
measurement shots are captured for each frame. Fig. 6 presents a timeline that illustrates this concept. It can be noticed that a detector with integration time 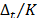 is assumed.
is assumed.
Consequently, eq. (8) can be rewritten to index the measurement shots. Thus, the 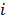 -th shot correspondent to the
-th shot correspondent to the 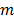 -th frame is expressed as
-th frame is expressed as
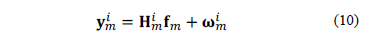
for 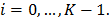 Here,
Here, 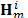 represents the sensing matrix and corresponds to the
represents the sensing matrix and corresponds to the 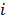 -th shot for the
-th shot for the 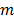 -th frame. Similarly, all the measurement shots captured for a single frame can be arranged as
-th frame. Similarly, all the measurement shots captured for a single frame can be arranged as 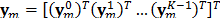 such that the multi-shot sensing approach can be expressed as in eq. (9) with
such that the multi-shot sensing approach can be expressed as in eq. (9) with 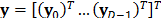 . However,
. However, 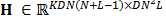 in this case is the sensing matrix that is associated with the full data using
in this case is the sensing matrix that is associated with the full data using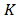 measurement shots, and is given by the expression
measurement shots, and is given by the expression
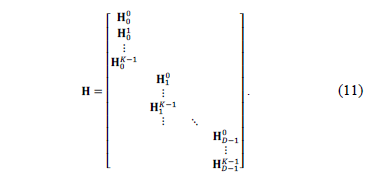
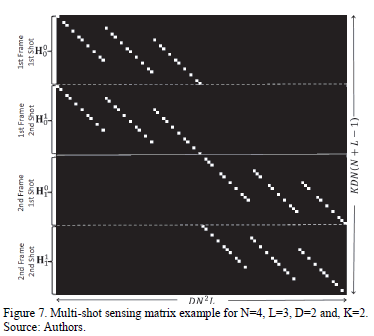
Fig. 7 shows an example of this matrix for 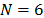 ,
, 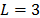 spectral bands,
spectral bands, 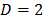 frames and,
frames and, 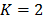 shots. The upper half of this matrix corresponds to the first frame and the lower half matrix accounts for the second frame. As in Fig. 5, each diagonal stands for a spectral band.
shots. The upper half of this matrix corresponds to the first frame and the lower half matrix accounts for the second frame. As in Fig. 5, each diagonal stands for a spectral band.
The set of measurements 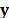 is then used to obtain a reconstruction of the underlying 4-dimensional data. This reconstruction is attained by solving the inverse problem
is then used to obtain a reconstruction of the underlying 4-dimensional data. This reconstruction is attained by solving the inverse problem 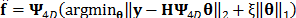 , where
, where 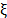 is a regularization constant,
is a regularization constant, 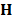 is the sensing matrix in eq. (11) and,
is the sensing matrix in eq. (11) and,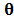 is a sparse representation of
is a sparse representation of 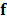 on the basis
on the basis 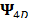 .
.
4. Simulations and Results
Simulations were performed in order to first determine the basis that provides the sparsest representation of dynamic spectral images and, second to test the model to sense and recover these types of images using CSI. All the simulations used a test data base composed by 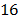 frames, each of them with
frames, each of them with 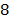 spectral bands and
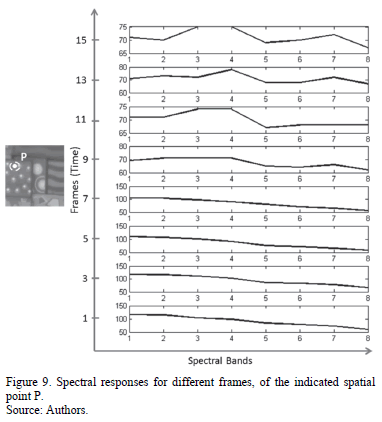
spectral bands and 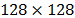 pixels of spatial resolution [20]. An RGB false color representation of the frames in this data base is presented in Fig. 8. In addition, the spectral responses of a specific point in the scene over time are depicted in Fig. 9. Random coded aperture patterns were used for all the experiments, in particular the entries of these patterns are realizations of a Bernoulli random variable with parameter
pixels of spatial resolution [20]. An RGB false color representation of the frames in this data base is presented in Fig. 8. In addition, the spectral responses of a specific point in the scene over time are depicted in Fig. 9. Random coded aperture patterns were used for all the experiments, in particular the entries of these patterns are realizations of a Bernoulli random variable with parameter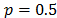 . All simulations were conducted using an Intel Core i7 3.6 GHz processor and, 64 GB RAM memory.
. All simulations were conducted using an Intel Core i7 3.6 GHz processor and, 64 GB RAM memory.
4.1. Sparse representations
Using eq. (2), different combinations of bases were tested for dynamic spectral scene representation. Previous results show that a Kronecker product between two-dimensional Wavelet Symmlet 8 and DCT bases provides a good sparse representation of spectral images [3,10]. Taking this into account, simulation results are presented for four combinations of Wavelet Symmlet 8 and DCT bases applied to the four dimensions of the test spectral video. More specifically, the kronecker product bases presented in Table 1 were tested.
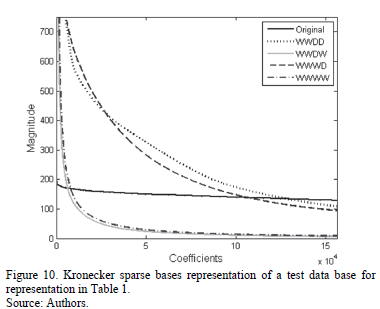
Fig. 10 shows the coefficients of the test data base on each basis from Table 1. It can be noticed that the bases WWWW and WWDW provide similar results, as do WWDD and WWWW. However, WWWW and WWDW coefficients experience a more pronounced decay, which indicates that these bases provide the sparsest representations.
The effect of using different bases can be also illustrated by obtaining an approximation of the original data base. This process consists of setting the smallest absolute value coefficients in the basis 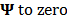 , while a percentage of the largest coefficients are preserved and, the reconstruction is obtained applying the inverse transformation.
, while a percentage of the largest coefficients are preserved and, the reconstruction is obtained applying the inverse transformation.
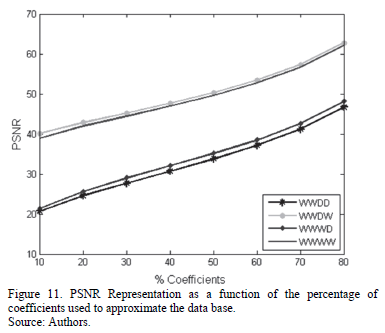
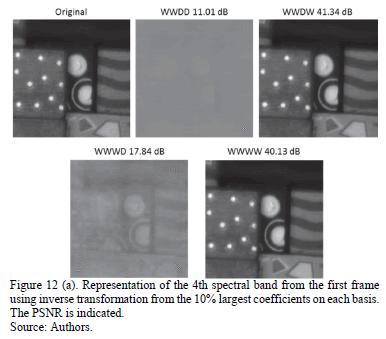
Fig. 11 shows the Peak Signal-to-Noise Ratio (PSNR) as a function of the percentage of coefficients used to approximate the underlying signal. It can be seen that the best PSNR results are obtained from the sparsest representations; the WWWW and WWDW bases improve the results by up to 30 dB. A comparison of the representations obtained from the different bases, using just the 10% largest coefficients, is shown in Fig. 12(a).
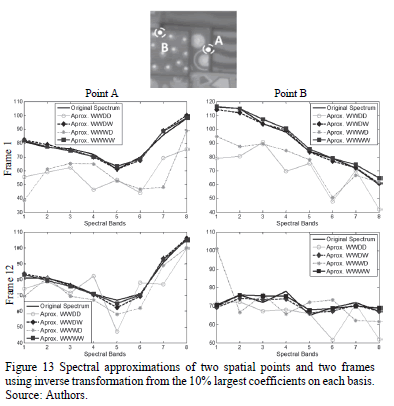
These approximations correspond to a portion of the fourth spectral band from the first frame. As previously mentioned, WWWW and WWDW bases provide accurate quality representations, while objects in the results from the other bases are hardly visible. Similarly, Fig. 12(b) presents the representations obtained from the 50% largest coefficients. It can be seen that a clearer approximation is obtained for all bases. However, the WWWW and WWDW bases still provide better results. In addition, the spectral and temporal approximations for two spatial points of the scene are illustrated in Figs. 13, 14, respectively. These figures demonstrate that the WWDW and WWWW bases provide the most accurate representations of the spectral video signal.
4.2. Reconstruction of dynamic spectral scenes
Several measurement shots were simulated to test the model presented in eq. (9) and eq. (11). In these cases, WWDW and WWWW, the representation bases that provide the sparsest approximations of the scene were used.
The procedure followed in this experiment consists of simulating the measurement set using the multi-shot model described in section 3.1. Then, the measurement set is used as the input of a compressed sensing reconstruction algorithm to obtain an approximation of the original scene. Specifically, the GPSR algorithm was used to solve the inverse problem [31].
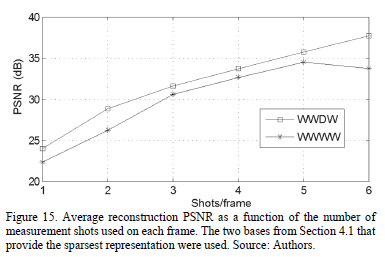
Fig. 15 shows the reconstruction PSNR as a function of the number of measurement shots per frame, 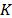 , used to obtain the reconstruction of the scene with
, used to obtain the reconstruction of the scene with 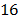 frames with
frames with 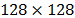 pixels and
pixels and 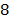 spectral bands. The PSNR values are calculated as the average of the PSNR for all the spectral bands and frames. It can be seen that for both representation bases, increasing the number of shots per frame leads to a higher PSNR value. However, the WWDW basis provides a slightly better PSNR value.
spectral bands. The PSNR values are calculated as the average of the PSNR for all the spectral bands and frames. It can be seen that for both representation bases, increasing the number of shots per frame leads to a higher PSNR value. However, the WWDW basis provides a slightly better PSNR value.
Fig. 16 shows the reconstruction of one spectral band obtained from different frames, using both representation bases. In general, this figure shows that both bases provide visually accurate reconstructions.
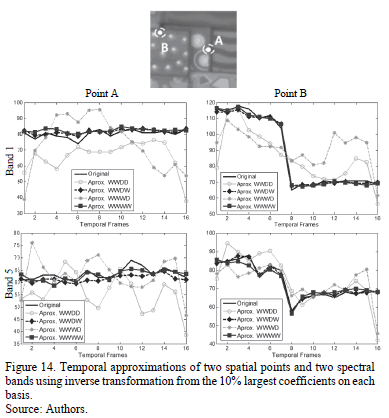
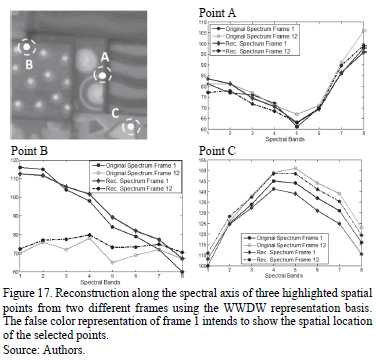
The performance of the multi-shot model can be demonstrated by comparing the spectral response of a specific point in the original scene with its correspondent reconstruction. Fig. 14 presents this comparison for three spatial points as indicated. Specifically, the spectral responses for these points measured in two different frames are shown. These results were obtained using the WWDW representation basis and 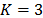 measurement shots per frame. Fig. 17 shows that this model provides an accurate spectral reconstruction. The false color representation of frame 1 intends to show the spatial location of the selected points.
measurement shots per frame. Fig. 17 shows that this model provides an accurate spectral reconstruction. The false color representation of frame 1 intends to show the spatial location of the selected points.
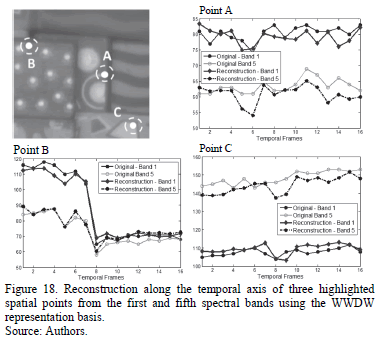
Similarly, a different strategy to show the accuracy of the model is to compare the behavior of the original scene measured at a specific spatial point and spectral band over time with the correspondent reconstruction. Fig. 18 shows the results for three points in the first and fifth spectral bands, as indicated. These results show that the reconstructions obtained are close representations of the original dynamic spectral scene.
5. Conclusions
A mathematical model for sparse representations of dynamic scenes in compressive spectral video sensing has been presented. Experiments show that the WWDW and WWWW bases provide the sparsest representations of these types of signals. A variation of the CASSI system for compressive spectral video sensing has been also presented. The mathematical models for single-frame and multi-frame capture with the CASSI system have been proposed. Simulation results show the accuracy of the model in spatial, spectral and temporal reconstructions. In general, reconstruction PSNR values of around 30 dB were obtained with the proposed model.
Acknowledgements
The authors gratefully acknowledge the Vicerrectoría de Investigación y Extensión at the Universidad Industrial de Santander and, the University of Delaware for supporting this work registered under the project title "Optimal design of coded apertures for compressive spectral imaging", VIE code 1368.
References
[1] Sarinova, A., Zamyatin, A. and Cabal, P., Lossless compression of hyperspectral images with pre-byte processing and intra-bands correlation. DYNA, 82(190), pp. 166-172, 2015. DOI: 10.15446/dyna.v82n190.43723 [ Links ]
[2] Arce, G.R., Brady, D.J., Carin, L., Arguello, H. and Kittle, D., An introduction to compressive coded aperture spectral imaging, IEEE Signal Processing Magazine, 31(1), pp. 105-115, 2014. DOI: 10.1109/MSP.2013.2278763 [ Links ]
[3] Arguello, H. and Arce, G.R., Rank minimization code aperture design for spectrally selective compressive imaging, IEEE Trans. Image Processing, 22(3), pp. 941-954, 2013. DOI: 10.1109/TIP.2012.2222899 [ Links ]
[4] Candes, E.J. and Wakin, M.B., An introduction to compressive sampling, IEEE Signal Processing Magazine, 25(2), pp. 21-30, 2008. DOI: 10.1109/MSP.2007.914731 [ Links ]
[5] Wagadarikar, A.A., John, R., Willet, R. and Brady, D.J., Single disperser design for coded aperture snapshot spectral imaging, Applied Optics, 47(10), pp. B44-B51, 2008. DOI: 10.1364/AO.47.000B44 [ Links ]
[6] Arguello, H. and Arce, G.R., Code aperture optimization for spectrally agile compressive imaging, Journal Optical Society of America A, 28(11), pp. 2400-2413, 2011. DOI: 10.1364/JOSAA.28.002400 [ Links ]
[7] Wu, Y., Mirza, I.O., Arce, G.R. and Prather, D., Development of a digitalmicromirror- device-based multishot snapshot spectral imaging system, Optics Letters, 36(14), pp. 2692-2694, 2011. DOI: 10.1364/OL.36.002692 [ Links ]
[8] Kittle, D., Choi, K., Wagadarikar, A.A. and Brady, D.J., Multiframe image estimation for coded aperture snapshot spectral imagers, Applied Optics, 49(36), pp. 6824-6833, 2010. DOI: 10.1364/AO.49.006824 [ Links ]
[9] Rueda, H. and Arguello, H., Spatial super-resolution in coded aperture-based optical compressive hyperspectral imaging systems, Revista Facultad de Ingeniería, 67, pp. 7-18, 2013. [ Links ]
[10] Rueda, H., Arguello, H. and Arce, G.R., On super-resolved coded aperture spectral imaging. SPIE Conference on Defense, Security and Sensing, Baltimore, MD, USA, 2013. DOI: 10.1117/12.2015855 [ Links ]
[11] Arguello, H. and Arce, G.R., Colored coded aperture design by concentration of measure in compressive spectral imaging, IEEE Trans. on Image Processing, 23(4), pp. 1896-1908, 2014. DOI: 10.1109/TIP.2014.2310125 [ Links ]
[12] Cheng, S.Y., Park, S. and Trivedi, M.M., Multi-spectral and multi-perspective video arrays for driver body tracking and activity analysis, Comput. Vis. Image Underst., 106(2-3), pp. 245-257, 2007. DOI: 10.1016/j.cviu.2006.08.010 [ Links ]
[13] Van-Nguyen, H., Banerjee, A. and Chellappa, R., Tracking via object reflectance using a hyperspectral video camera, in 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition - Workshops, CVPRW 2010, pp. 44-51. 22, 2010. DOI: 10.1109/CVPRW.2010.5543780 [ Links ]
[14] Banerjee, A., Burlina, P. and Broadwater, J., Hyperspectral video for illumination-invariant tracking, in WHISPERS '09 - 1st Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, 2009. DOI: 10.1109/WHISPERS.2009.5289103 [ Links ]
[15] Duran, O. and Petrou, M., Subpixel temporal spectral imaging, Pattern Recognition Letters, 48, pp. 15-23, 2014. DOI: 10.1016/j.patrec.2014.04.005 [ Links ]
[16] Leitner, R., De-Biasio, M., Arnold, T., Dinh, C.V., Loog, M. and Duin, R.P.W., Multi-spectral video endoscopy system for the detection of cancerous tissue, Pattern Recognition Letters, 34(1), pp. 85-93, 2013. DOI: 10.1016/j.patrec.2012.07.020 [ Links ]
[17] Zuzak, K.J., Naik, S.C., Alexandrakis, G., Hawkins, D., Behbehani, K. and Livingston, E., Intraoperative bile duct visualization using near-infrared hyperspectral video imaging, Am. J. Surg., 195(4), pp. 491-497, 2008. DOI: 10.1016/j.amjsurg.2007.05.044 [ Links ]
[18] Arnold, T., De Biasio, M. and Leitner, R., Hyper-spectral video endoscopy system for intra-surgery tissue classification, in Proceedings of the International Conference on Sensing Technology, ICST, pp. 145-150, 2013. DOI: 10.1109/ICSensT.2013.6727632 [ Links ]
[19] Yi, D., Kong, L., Wang, F., Liu, F., Sprigle, S. and Adibi, A., Instrument an off-shelf CCD imaging sensor into a handheld multispectral video camera, Photonics Technology Letters, IEEE, 23(10), pp. 606-608, 2011. DOI: 10.1109/LPT.2011.2116153 [ Links ]
[20] Mian, A. and Hartley, R., Hyperspectral video restoration using optical flow and sparse coding, Optics Express, 20(10), pp. 10658-10673, 2012. DOI: 10.1364/OE.20.010658 [ Links ]
[21] Cao, X., Tong, X., Dai, Q. and Lin, S., High resolution multispectral video capture with a hybrid camera system, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2011, pp. 297-304, 2011. DOI: 10.1109/CVPR.2011.5995418 [ Links ]
[22] Du, H., Tong, X., Cao, X. and Lin, S., A prism-based system for multispectral video acquisition, 2009 IEEE 12th International Conference on Computer Vision, pp. 175-182, 2009. DOI: 10.1109/ICCV.2009.5459162 [ Links ]
[23] Cao, X., Du, H., Tong, X., Dai, Q. and Lin, S., A prism-mask system for multispectral video acquisition, IEEE Transactions on Pattern Analysis and Machine Intelligence, 33(12), pp. 2423-2435, 2011. DOI: 10.1109/TPAMI.2011.80 [ Links ]
[24] Llull, P., Liao, X., Yuan, X., Yang, J., Kittle, D., Carin, L., Sapiro, G. and Brady, D.J., Coded aperture compressive temporal imaging, Optics Express, 21(9), pp. 10526-10545, 2013. DOI: 10.1364/OE.21.010526 [ Links ]
[25] Xu, L., Sankaranarayanan, A., Studer, C., Li, Y., Baraniuk, R.G. and Kelly, K.F., Multi-scale compressive video acquisition, in Imaging and Applied Optics, OSA Technical Digest, 2013. DOI: 10.1364/COSI.2013.CW2C.4 [ Links ]
[26] Llull, P., Liao, X., Yuan, X., Yang, J., Kittle, D., Carin, L., Sapiro, G. and Brady, D.J., Compressive sensing for video using a passive coding element, in Imaging and Applied Optics, OSA Technical Digest, 2013. DOI: 10.1364/COSI.2013.CM1C.3 [ Links ]
[27] Koller, R., Schmid, L., Matsuda, N., Niederberger, T., Spinoulas, L., Cossairt, O., Schuster, G. and Katsaggelos, A.K., High spatio-temporal resolution video with compressed sensing, Opt. Express, 23(12), pp. 15992-16007, 2015. DOI: 10.1364/OE.23.015992 [ Links ]
[28] Tsai, T., Llull, P., Carin, L. and Brady, D.J., Spectral-temporal compressive imaging, Optics Letters, 40(17), pp. 4054-4057, 2015. DOI: 10.1364/OL.40.004054 [ Links ]
[29] Tsai, T., Llull, P., Yuan, X., Carin, L. and Brady, D.J., Coded aperture compressive spectral-temporal imaging, Imaging and Applied Optics 2015, OSA Technical Digest, 2015. DOI: 10.1364/COSI.2015.CTh2E.5 [ Links ]
[30] Galvis-Carreño, D., Mejia-Melgarejo, Y. and Arguello-Fuentes, H., Efficient reconstruction of Raman spectroscopy imaging based on compressive sensing. DYNA, 81(188), pp. 116-124, 2014. DOI: 10.15446/dyna.v81n188.41162 [ Links ]
[31] Figueiredo, M., Nowak, R. and Wright, S., Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems, IEEE Journal in Selected Topics in Signal Processing, 1(4), pp. 586-597, 2007. DOI: 10.1109/JSTSP.2007.910281 [ Links ]
C.V. Correa-Pugliese, received her BSc. Eng. in Computer Science in 2009, her MSc. in Systems Engineering in 2013, both from the Universidad Industrial de Santander (UIS), Colombia. She received her MSc. degree in Electrical Engineering from the University of Delaware in 2013. She is currently a PhD candidate in the Electrical and Computer Engineering Department at the University of Delaware, USA. Her research interests include compressive spectral imaging, computational imaging, and compressed sensing. ORCID: 0000-0002-1812-287X.
D.F. Galvis-Carreño, received her BSc. Eng. in Chemical Engineering in 2011 from the Universidad Industrial de Santander (UIS), Colombia. She is currently pursuing her MSc. in Chemical Engineering at UIS. Her main research areas include compressive raman spectroscopy, compressed sensing and, image processing. ORCID: 0000-0002-0392-1281.
H. Arguello-Fuentes, received his BSc. Eng. Electrical Engineering in 2000, his MSc. in Electrical Power in 2003, both from the Universidad Industrial de Santander (UIS), Colombia. He received his PhD in Electrical Engineering from the University of Delaware, USA in 2013. He is an associate professor in the Department of Systems Engineering at the Universidad Industrial de Santander, Colombia. His research interests include high-dimensional signal processing, optical imaging, compressed sensing, hyperspectral imaging, and computational imaging. ORCID: 0000-0002-2202-253X.