Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.195 Medellín jan./fev. 2016
https://doi.org/10.15446/dyna.v83n195.47027
DOI: http://dx.doi.org/10.15446/dyna.v83n195.47027
Forecasting of short-term flow freight congestion: A study case of Algeciras Bay Port (Spain)
Predicción a corto plazo de la congestión del flujo de mercancías: El caso de estudio del Puerto Bahía de Algeciras (España)
Juan Jesús Ruiz-Aguilar a, Ignacio Turias b, José Antonio Moscoso-López c, María Jesús Jiménez-Come d & Mar Cerbán e
a Intelligent Modelling of Systems Research Group, University of Cádiz, Algeciras, Spain. juanjesus.ruiz@uca.es
b Intelligent Modelling of Systems Research Group, University of Cádiz, Algeciras, Spain. ignacio.turias@uca.es
c Intelligent Modelling of Systems Research Group, University of Cádiz, Algeciras, Spain. joseantonio.moscoso@uca.es
d Intelligent Modelling of Systems Research Group, University of Cádiz, Algeciras, Spain. maríajesus.come@uca.es
e Research Group Transport and Innovation Economic, University of Cádiz, Algeciras, Spain. mariadelmar.cerban@uca.es
Received: November 04rd, 2014. Received in revised form: June 12th, 2015. Accepted: December 10th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The prediction of freight congestion (cargo peaks) is an important tool for decision making and it is this paper's main object of study. Forecasting freight flows can be a useful tool for the whole logistics chain. In this work, a complete methodology is presented in order to obtain the best model to predict freight congestion situations at ports. The prediction is modeled as a classification problem and different approaches are tested (k-Nearest Neighbors, Bayes classifier and Artificial Neural Networks). A panel of different experts (post-hoc methods of Friedman test) has been developed in order to select the best model. The proposed methodology is applied in the Strait of Gibraltar's logistics hub with a study case being undertaken in Port of Algeciras Bay. The results obtained reveal the efficiency of the presented models that can be applied to improve daily operations planning.
Keywords: freight forecasting; classification; congestion; artificial neural networks; multiple comparison tests.
Resumen
La predicción de la congestión en el tráfico de mercancías (picos de carga) es una importante herramienta para la toma de decisiones y es el principal objetivo de este trabajo. Predecir los flujos futuros de mercancías proporciona una potente herramienta en la cadena de suministro. En este trabajo, se presenta una metodología para conseguir el mejor modelo para predecir situaciones de congestión en flujos de mercancías. La predicción es modelada como un problema de clasificación, evaluando diferentes métodos (K-vecinos, clasificador Bayesiano y Redes Neuronales Artificiales). Para seleccionar el mejor modelo se desarrolla un panel de expertos (mediante métodos post-hoc del test de Friedman). La metodología propuesta se aplica a la cadena logística del Puerto Bahía de Algeciras. Los resultados obtenidos revelan la eficiencia de los modelos presentados, que pueden ser aplicados para mejorar la planificación diaria de operaciones.
Palabras clave: predicción de mercancías; clasificación; congestión; redes neuronales artificiales; test de comparación múltiple.
1. Introduction
Freight volume forecasting is a crucial component of the transportation system that can be used to improve the service quality and the operation planning in order to make correct decisions and support the system management. The flow of goods is one of the most important aspects in transport systems, and understanding the transport chain is central to its management, planning, improving facilities and operations [1]. Currently, companies that have a relationship with transportation require updates in terms of time to maximize their operating profit and also to improve the level of service [2].
The organization of multimodal transportation is complex because there are many actors involved in the supply chain. In this type of organization, in which there are many elements, the principal problem is information [3]. The availability of information about transport systems is vital to analyze trends [4]. Improving the quality of information using freight traffic predictions could be crucial in the short-term decision-making process.
Many studies have analyzed short-term forecasting problems pointing out the importance of prediction in different fields of research [5-9]. Short-term forecasting models can be categorized into two groups, depending on the kind of problem to be considered: regression or classification models [10]. Many of the studies relating to forecasting traffic flows can be found in maritime transport literature. The main focus of these papers was the avoidance of congestion problems. The large increase in trade has caused significant impacts in the supply chain operations, increasing traffic congestions and time delays in freight transport [11]. Many ports are congested and consequently costs are raised, which affects competitiveness. These effects can divert traffic to other more competitive ports [12]. Short-term predictions have been used to facilitate the implementation of daily port operation activities, such as the allocation and provision of personnel and necessary equipment for the proper planning of daily operations [13]. In this context, a prediction of certain traffic flows that lead to congestion could be a powerful tool to avoid those situations. Owing to the lack of literature relating to predicting freight congestion, a brief literature review on the proposed methods and other techniques for transportation problems was included in this paper.
There are, however, a wide range of works related to predicting traffic flows in transport using regression models [14-17]. Numerous types of methodologies have been used in the literature to predict traffic flows in shipping or maritime transport. Classic techniques such as regression analysis, classic decomposition or univariate forecast models (ARIMA) have been applied for years by several authors who have obtained satisfactory results. Seabrooke et al. [18] employed regression analysis to predict load growth in Hong Kong Port in Southern China. Similarly, Chou et al. [19] proposed a modified regression model to predict the volume of import containers in Taiwan. Fung [20] developed a forecasting model to predict the movement of containers in Hong Kong port and to provide a more accurate prediction than the one offered by the authorities. Klein [21] tried to find a model to predict the flow of maritime traffic in total tonnage in the Antwerp Port. Peng and Chu [13] performed a comparative analysis between different prediction models in order to find the most accurate model to predict container volumes. Ruiz-Aguilar et al. [22] developed a multi-step procedure to predict the number of freight inspections at ports. Finally, Yang et al. [23] modeled the road traffic in a Chinese container port environment, and the results indicated that the model had a high estimation quality at peak traffic times.
Many transport systems problems are represented as non-linear phenomena, which come from many sources and contain complex data. These nonlinear phenomena are difficult to plot in a dynamic context and are subject to constant changes. In this context, artificial neural networks (ANNs) have been used to model traffic flows due to their adaptability, nonlinearity and arbitrary function mapping capability. Therefore, several authors pointed out that the utilization of ANNs can provide a competitive advantage for planning and forecasting in transportation research [8,24-26]. Recent studies have introduced the use of intelligent and nonlinear techniques (specifically ANNs) for predicting and estimating maritime traffic flows, showing better results in comparison with classical statistical models. Lam et al. [27] applied neural network models to several types of goods movements in Hong Kong port, comparing the prediction performance with the one obtained with the classical regression methods. The results show that neural network prediction was more reliable. Recently, Gosasang et al. [28] suggested the use of an MLP model as a technique for predicting the volume of containers at Bangkok port. Furthermore, this author made a comparison with classic techniques that had, up to that point, been used to make calculations for the port.
Moreover, there are not many studies in the literature related to transport using classification methods to forecast congestion episodes of traffic flows, especially for maritime transport. Examples of these models are the well-known k nearest neighbor (k-NN) and the Bayesian Classifier (BC) models, which are widely, used classification techniques. As such, Robinson and Polak [29] used the k nearest neighbor method in order to model the urban link travel time in the city of London. The results provide a more accurate estimation than other techniques. More recently, k-NN was compared to other techniques in Bhave and Rao's work [30]. The authors studied the acoustic signatures of vehicle detection, providing traffic congestion estimations. Furthermore, [31] used a k-NN classification in a hybrid procedure, which involves other techniques such as multiple regression and principal component analysis in order to determine urban road categories using real traffic flow data.
Moreover, BC are proposed in several areas of transportation. Travel time forecasting has been emphasized by some authors. Thus, [32] a simple Bayesian estimator to forecast arterial link travel speed in Jeonju (China) was developed. Furthermore, a Naïve Bayesian Classification model was also used by Chowdhury et al. [33] for the same purpose. The Bayesian classifier has been applied with successful results in the area of transport security. Thus, a model based on BC was developed by Boyles et al. [34] in order to anticipate incident duration, whereas Oh et al. [35] proposed a nonparametric Bayesian model to estimate the likelihood of an accident in real-time from empirical data in California (US). More recently, other studies relating to transportation have identified the occupant postures in vehicles in order to reduce the risk of injuries [36], or vehicle classification using Bayesian networks [37].
Intelligence methods have also been successfully applied in classification problems related to transport. Particularly, ANNs have demonstrated good performances due to their inherent capabilities in classification tasks. In this sense, neural classifiers based on ANNs were employed in order to detect operational problems on intersections and signalized urban arterials [38] and to detect freeway incidents using probabilistic neural networks [39]. This kind of neural network classifier was also proposed by Abdel-Aty and Pande [40] to improve the identification of patterns in a freeway that could forecast potential crashes. Moreover Wu et al. [41] adopted a multi-layer perceptron network, which was used to recognize and classify vehicles.
The main objective of this work is the prediction of peak loads in order to avoid congestion in port nodes. The authors have made a comparison between the above mentioned three different peak prediction techniques applied to Roll-on/Roll-off (Ro-Ro) traffic: k-NN, BC and ANNs. Multiple comparison tests have been used as an expert panel in order to find the best model to predict the peak volume of short-term (one-day ahead) traffic in the Strait of Gibraltar, which is the study case. To the best of our knowledge, classification techniques to predict workload peaks have not yet been proposed in the research literature.
The remainder of this paper is organized as follows: Section 2 presents the study area and the database; Section 3 describes the forecasting models used in this work and the methodology to investigate the performance of the different models; Section 4 analyzes the results obtained by the proposed methodology; and Section 5 presents the conclusions.
2. Materials and methods
The different proposed models were tested in the Strait of Gibraltar's logistics hub. The Strait of Gibraltar's geostrategic position means it is one of the main maritime routes for carriers, and consequently one of the most intense maritime traffic points.
Furthermore, the Strait of Gibraltar is the bridge between Africa and Europe. In 2012, 116,690 vessels crossed the Strait of Gibraltar, of which 40,214 ships connected African and European ports. Traffic on both sides consists essentially of passenger and Ro-Ro traffic. The distance between the ports on the Strait is only 12 miles and this makes transport from northern Africa to Europe more effective because of the close location. In 2012 there were 4,692,889 tons of good moved on this route. The Algeciras bay Port is in the top 10 Europe ports in terms of high Ro-Ro volume. As the main entry point of goods from Africa, the Algeciras Bay Port is in charge of managing their entrance to the EU, and also exercising several controls (health, industrial or tax) that are performed in the Border Inspection Posts (BIPs). Perishable goods are the most important traffic in this port. Due to this, freight transit must be performed in the most effective way possible. Hence, the proposed prediction model can add value to the supply chain management. It is important to adopt models to ease the process and to facilitate transshipment procedures.
The information used to develop this work is taken from a database provided by the Algeciras Bay Port Authority. The database contains all imports in Algeciras during the study period: between 2000 and 2007, and it was initially composed of more than three million records. After an extensive preprocessing stage was performed, the final database contained 2,970 daily records from January 2000 to December 2007. This work focuses on the first chapter (vegetables), which are the freight that is most frequently inspected in the BIP. The Border Inspection Post has a mean workload of 7000 ton/day. The main focus is to determine when the daily freight volume of vegetables increases over certain level (freight peak). Therefore, the forecasting tool can be used to avoid congestions, delays and cost increments. Stakeholders can use forecasts to help with resource planning.
After the preprocessing and review of the database, a daily increment of 400 tons was selected as a peak level, since this value diminished the performance of the system (the total time at BIP). More staff would be assigned during these peak levels of service in order to avoid congestion.
An autocorrelation analysis has been undertaken in order to determine what the most important lags (time delays) have been in the past (more informative). As time progresses the autocorrelation coefficient decreases. There is only an increment detected when the lag coincides with the day of the week. Therefore, lags = 1, 2, 7, 14, 21 and 28 have been chosen as experimental autoregressive window size (n) to be tested.
The database of samples used to teach the forecasting models was arranged in the form of autoregressive data (see Eq. (1), where n was the width of the observation window in the past (lags).
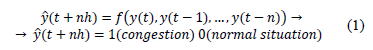
This information was used to make the prediction, as it uses autoregressive models. In this case, nh was the time horizon when freight peak is predicted. That is, nh=1 means a one day-ahead prediction. The prediction for this work was 1-ahead (short-term), for which different prediction models and autoregressive inputs have been combined (see Table 1)
3. Methodology
The forecasting of freight peaks can be developed using a classification scheme between two categories (freight peaks and normal situations). Classification is the inferring of meaning (category, class) from observations. There are two basic stages when designing a classifier: the training (or design) phase and the test (generalization or application) phase. The result of the training phase is the set of classifier parameters that define the discriminant functions that form the class boundaries between disjoint class or category regions.
3.1. Bayes classifiers
Bayesian classifiers are based on probability theory and they give the theoretical basis for pattern classification [42]. The decision rules based on the Bayes theorem are optimal [43], but they are unattainable in practice because the complete information about the statistical distributions of each class is unknown. However, they do provide the logical basis for all statistical algorithms.
The statistical procedures attempt to provide the information about the distribution of two ways: parametric and non-parametric. The first way makes some assumptions about the nature of the distributions, and their parameters must be estimated. The latter is distribution-free.
We assume that the prior probabilities and the probabilities associated with each class are known. Thereafter, in order to calculate a posteriori probabilities P(A|X) and P(B|X) the Bayes' theorem is used. Pattern is classified as A if P(A|X) > P(B|X), otherwise the pattern will be classified as B. This is equivalent to classify a pattern within class A if P(X|A)·P(A)>P(X|B)·P(B). If it is further assumed that P(A) = P(B), then P(X|A) > P(X|B). Assuming that the conditional probabilities are statistically independent and follow normal distributions with identical variances, ||X-mA||<||X-mB|| can be obtained (mA and mB are the class means), which is a minimum distance-based classifier. The equation of the decision function is ||X-mA|| = ||X-mB||. This method is known as naive Bayes, if variable independence is assumed [44].
More generally, it is possible to assume variable dependence and therefore there is a covariance matrix of the variables. In this case, two hypotheses can be assumed. One is that the model has the same covariance matrix for each class (homoscedasticity assumption) and the mean of each class vary (LDA: Linear Discriminant Analysis). The other is that the covariance and the mean of each class vary (QDA: Quadratic Discriminant Analysis) [45]. Both hypotheses have been used in this work.
3.2. k - Nearest neighbors
Nearest neighbor classifier is a well-known non-parametric method in pattern recognition [46]. These classifiers use all the available data as templates for classification. In the simplest form, for a given input vector, a nearest neighbor classifier searches the nearest template and classifies the input vector into the class to which the template belongs. In a more complex form, the classifier uses k nearest neighbors.
This algorithm does not have a training phase off line. The idea is to store the available data set, so that when a new instance is classified the algorithm searches for similar cases in the stored examples and assigns the most likely class. A common way to find the closest examples is through the Euclidean distance. In order to prevent ties, an odd number of neighboring observations are used in this work (k=1,3 or 5).
3.3. Neural networks for classification
A multilayer perceptron (MLP) feedforward network trained with backpropagation algorithm [47] are capable of approximating any non-linear mapping with arbitrary accuracy. In this sense, multilayer feedforward networks are universal approximators [48]. Multi-Layer Perceptron (MLP) based on backpropagation learning procedure is the most commonly used artificial neural network in numerous applications, including classification [49,50]. Gradient descent algorithms have some drawbacks that can be avoided with second-order Newton based methods [51]. The Levenberg-Marquardt algorithm was designed to approach second-order training speed without the need to compute the Hessian matrix, and it uses an approximation applying the Jacobian matrix of first derivatives. The application of Levenberg-Marquardt to ANN training is described in the work of Hagan and Menhaj [52]. This algorithm appears to be the fastest method for training moderate-sized feedforward neural networks, and it is used in this work.
In such a feedforward network, the output vector y is a function (non-linear) of the input vector X, and some weights w Training (or designing) the network involve searching in the weight space of the network for a value of w that produces a function which fits the provided training data.
The training process is a function minimization (i.e., adjusting w in such a way that the objective function E is minimized). For general feedforward neural networks, the backpropagation algorithm evaluates the gradient of the output y to update w (weights) by eq. (2) (where a is the learning rate).
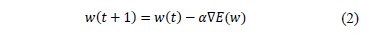
3.4. Evaluation
Generalization error is the estimation of the accuracy of learning algorithms that explains how well a learning machine generalizes with different data from the training process. The experimental procedure for each proposed model was repeated 20 times in order to compare the different models and to determine (by analyzing the mean and the variance of the indexes) the best one.
In order to compare the generalization error of learning algorithms, statistical tests have been proposed. To compare the different classification models in the experiments, different evaluation parameters can be used:
- Accuracy (ACC) is defined as the ratio between the sum of true results (number of peaks and non-peaks correctly predicted) against the total number of samples in the data series.
- Precision (PR) is defined as the proportion of the true positive against all the positive results.
The values of these indexes are in the interval [0-1]. An accuracy of 100% means that the measured values are exactly the same as the given values. Accuracy is how close to "true" measurements these values are. Precision is how consistent the results are over several measurements, or how repeatable the model is.
3.5. Multiple comparison of models
ANOVA test is a well-known statistical method for testing the differences between more than two related sample means. ANOVA divides the total variability into the variability between the models, variability between the data sets and the residual (error) variability. The null-hypothesis is that there are no differences between the models. If the between-models variability is significantly larger than the residual variability, the null-hypothesis can be rejected and it can be concluded that there are some differences between the models. ANOVA is based on assumptions that are most probably difficult to assure. First, ANOVA assumes that the samples are drawn from normal distributions. In general, there is no guarantee for normality in the results of the classifiers. The second and more important assumption of ANOVA is homoscedasticity, which requires the random variables to have equal variance. The Friedman test [53,54] is the nonparametric equivalent of ANOVA test, without the need to ensure assumptions of normality and homoscedasticity.
The issue of multiple hypothesis testing is a well-known statistical problem. The usual goal is to decrease the probability of making at least one Type 1 error in any of the comparisons. If the null-hypothesis is rejected, a post-hoc test can be used. Salzberg [55] states a general solution for the problem of multiple testing, the Bonferroni method, and notes that it is usually very conservative. Pizarro et al. [56] use ANOVA and Friedman's test to compare multiple models (in particular, neural networks) on a single data set. The authors of this paper have also used the ANOVA and Bonferroni methods successfully in previous works [57,58].
The oldest and most popular technique to undertake these multiple comparisons procedure is the LSD (Least Significant Difference) detailed in Fisher [59]. This method determines the difference LSD (See eq. 3).

- Which follows a t-distribution with degrees of freedom N-I. I is the number of models, ni and nj are the number of observations for each mean mi and mj. The a parameter is the statistical significance or the probability of making a Type I error and SR is the estimation (mean square) of error variability.
The drawback of LSD is that it has the highest probability of making rejections, which increases with the number of comparisons performed. To avoid this problem, other procedures have been introduced to make multiple comparisons. These methods are based on the Bonferroni inequality. This procedure sets a significance level a that is shared between each of the comparisons taken into consideration. It would be better not to use the Bonferroni method when the number of pairwise comparisons is very large because the level of significance of each comparison may become too small to be considered useful. Another method is based on the Studentized range (q), which results in the significant difference method proposed by Tukey [60], also called HSD method (Tukey Honest Significant Difference), using the HSD difference shown in the following equation.
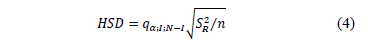
Fisher's LSD method is the one that provides the most significant difference, and is followed by Tukey's method. The method to be applied depends on the risk to be assumed; that is, accepting as significant differences those that are not (less conservative situation), or accepting less significant differences that do actually exist. Carmer and Swanson [61] conducted simulation studies by the Monte Carlo method, which concluded that the LSD procedure is a very efficient test to detect true differences. In this work, these methods have been used as an expert panel in order to consider their individual decisions and to ensemble a global rule.
In the case that there are no significant differences, Occam's razor's criterion should be used. Occam's razor is the principle that states a preference for simple theories: "Accept the simplest explanation that fits the data".
3.6. Validation and experimental design
A resampling strategy was developed in order to compare different models and to determine if difference among the models exists [56,62].
It is necessary to measure several test sets in which the examples have not been used in the training phase. There are a range of methods to achieve suitable validation of the results (cross-validation, bootstrap, etc.); specifically, two-fold cross-validation (2-CV), which divides the database into two disjointed sets (training and test). The two fold cross-validation procedure was applied to the database in this research.
The model parameters are determined (coefficients, weights, etc.) with the first set, and the error measures that have been established (precision and accuracy e.g.) are computed with the second one. Subsequently, the sets are inverted and the same operations are re-performed, and the average of the two experiments is obtained. This procedure was repeated 20 times in order to calculate the average quality measurements in this experiment. It is the most pessimistic validation technique as it leaves out the half the data to calculate the measures of generalization error. Therefore, any other validation method will provide better results. Thus, the results with 2-CV can be considered as a minimum value of the actual results. The authors have previously successfully applied this procedure in different applications [26,63].
In order to study the peak prediction of Ro-Ro traffic in Algeciras Bay Port of, three different classification methods have been tested: Bayesian classifiers (Linear and Quadratic Discriminant Analysis), K-Nearest Neighbors (K =1,3,5) and ANNs (with different numbers of hidden units and different epochs). The complete set of models can be shown in Table 1. In this work, 120 models have been tested in order to select the best forecasting performance. For each of the 20 models in Table 1, different inputs have been used. In each case, a different number (n) of lagged data has been used as inputs for the prediction model (different sizes of this autoregressive information window n=1, 2, 7, 14, 21 and 28). Actually, a greater number of inputs does not guarantee better results. This fact will be confirmed with the results that were obtained in the experimental design. The random resampling experiment explained above has been applied to calculate the average quality indexes in order to compare results.
4. Results and discussion
Comparing the different models tested, generalization error has been checked in order to select the model with the minimum error. This can be achieved by calculating the mean of the accuracy and precision values for test samples with different autoregressive window sizes.
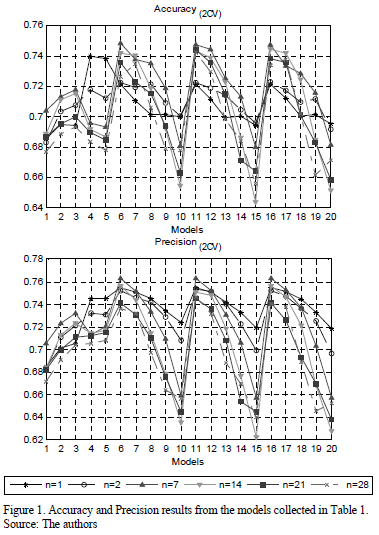
The results are presented graphically in Fig. 1. It can be observed that the best network input configurations are obtained generally with n=1 and n=7 autoregressive window sizes, which exceed values of 0.75 for accuracy and 0.76 for precision. The worst results are obtained for n=28 which indicates that introducing a higher size of autoregressive window does not improve the prediction.
In those models based on K-NN, as parameter K increases, the results of the model improve. More stable results are obtained with the Bayesian models. In this case, the different functions studied (LDA and QDA) provide similar results. Moreover, for those models based on ANNs, it can be observed that the number of epochs used in the training stage is not very relevant. However, the selection of optimal number of neurons in hidden layer is crucial to find a balance between complexity and generalization error. Better results of precision and accuracy are obtained when the number of hidden neurons decrease, reducing the complexity of the classifier.
Models 6, 11 and 16 seem to be the best models after a preliminary visual analysis of Fig. 1. These models that are based on ANNs may be the optimal input configurations. Nevertheless, the best model must be chosen by using a statistical multiple comparison technique. Analysis of variance (ANOVA) techniques inform us about the existence of significant differences between the treatments. The Friedman Test is used for this goal instead of the ANOVA test due to its non-parametric properties. The Friedman test is an alternative to the ANOVA test, when the assumption of normality or equality of variance is not met. This, as is the case with many non-parametric tests, uses the ranks of the data rather than their raw values to calculate the statistic.
When the Friedman test reveals the existence of significant differences, it is necessary to analyze how the means differ. In order to achieve this, different techniques have been used (Fisher Least Significant Difference-LSD, Tukey's Honest Significant Difference-HSD and Bonferroni's method). The choice of the best model was made by contrasting the results obtained from each technique using a panel of experts.
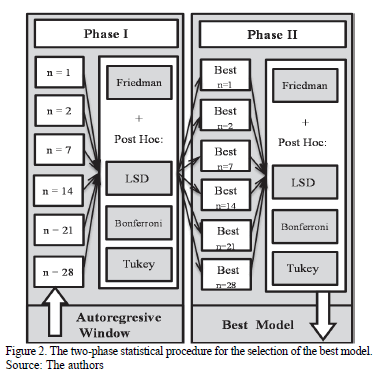
The selection of the best global model was undertaken in two phases. This two-phase procedure is showed in Fig. 2. Phase I deals with the application of statistical techniques previously described (Friedman + post hoc test) in order to point out which autoregressive window size is the best one in each model. Phase II identifies the best global model (algorithm and parameters) using the same techniques. In Phase I, the quality indices (accuracy and precision) obtained for each model's different autoregressive windows have been compared by the Friedman test in order to verify the null hypothesis, with a significance level a=0.05. The results of the Friedman test reveal the existence of significant differences between the average of all the samples, hence the null hypothesis has been rejected. In other words, there are certain autoregressive windows that are better than others.
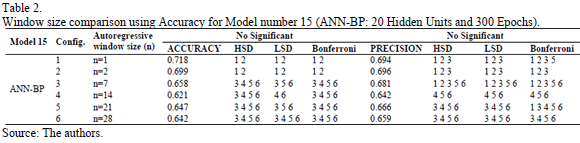
Therefore, it is necessary to apply multiple comparison methods in order to find out which of the models or groups of models are significantly better in terms of accuracy and precision. Tukey's HSD, Bonferroni's and Fisher's LSD tests have been applied as a panel of experts to obtain the results presented in Table 2 (only Model 15 is presented as an example for simplicity).
The first step has been to point out those input configurations that are significantly different from the rest. The three experts agree that for the accuracy index, the input configurations 1 and 2 (n=1 and n=2) are significantly different from the rest. In this case, the simplest computational model has been chosen (number 1). For precision values, the three experts agree that all the input configurations overlap one another. In this case, the input configuration with a better index should be chosen (n=2). Finally, due to the discrepancy between the selection of the better input configuration based on both quality indexes, an accuracy term was considered to be a critical criteria, which is due to the specific application of our research. In this work, the correct prediction of patterns of both classes it is the most relevant part (True Positives and True Negatives). Furthermore, in this study, false positive situations are preferable to false negatives because false negatives would produce overload and congestion situations decreasing the performance of the BIP system. Once the results obtained by Tukey's HSD, Fisher's LSD and Bonferroni's method for each of the 20 models have been analyzed, the best input configurations have been chosen for each one.
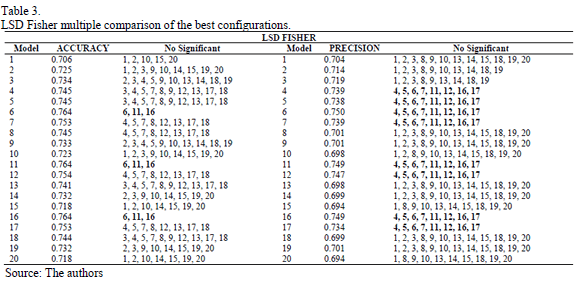
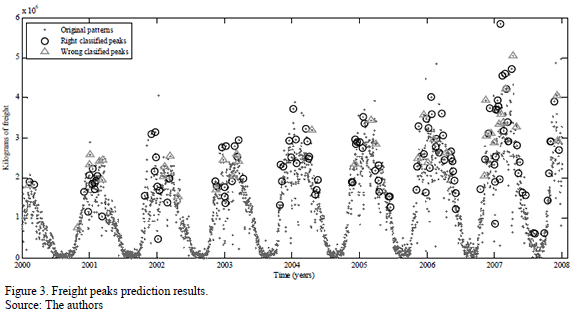
In Phase II, in order to obtain the best global model, the methodology explained above has been applied again for the best input configurations. The results obtained in Phase II reveal the existence of significant differences between the input configurations. Therefore, the null hypothesis has been rejected with a level of significance a=0.05. In order to find out which models are significantly different, the multiple comparison methods (Tukey's HSD, Fisher's LSD and Bonferroni's method) have once again been applied (as an expert panel). For Bonferroni's and Tukey's methods, all the models overlap; Fisher's LSD was the only one able to find differences between the groups. This is because it is a less conservative method than the others and offers more significant differences. The results obtained with Fisher's LSD are presented in Table 3. The HSD and Bonferroni methods have not been included due to the lack of space. The interpretation of the results collected in Table 3 shows that the best models are numbers 6, 11 and 16 (accuracy index). Therefore, the simplest model (number 6) can be selected as the best forecasting model based on Occam's razor rule. This model is a neural network with only one neuron in the hidden layer. In this sense, as the model is close to being linear and a more complex model (with a greater number of hidden neurons), it is not required. In Fig. 3, the results obtained for the best model (model number 6) can be observed. Results come from test data and one of the repetitions. The points on the graph correspond to the goods (measured in kg) that cross the Algeciras Bay Port on a daily basis. The circles correspond to right peaks predicted by the model and the triangles correspond to the misclassified ones.
5. Conclusions
A two-phase procedure has been carried out in order to find the best model to predict a significant increase in the amount of freight with the aid of a panel of statistical multiple comparison tests. In the first phase, the best autoregressive window can be selected, and in the second phase the best algorithm and its parameters are identified.
This panel of experts has been applied to a resampling procedure in order to measure the models' generalization error and then compare them using accuracy and precision indexes. In this way, the best model is an artificial neural network k with a three-layer structure with only one hidden unit using the Levenberg-Marquardt optimization method as a learning algorithm and an autoregressive window of n=7 as its input. Therefore, in this case, an ANN model achieves better performance than the Bayes classifier and KNN models. It is worth mentioning that the increase in complexity (adding hidden units) does not significantly improve the results. The Friedman non-parametric test rejected the null hypothesis and, therefore, it has been necessary to use post-hoc tests (Fisher's LSD, Tukey's HSD and Bonferroni's method). Fisher's LSD test has more power compared to other more conservative post-hoc comparison methods.
In this work, the risk consists of predicting a saturation situation when in reality does not happen. The only damage would be planning for a workload that was smaller than expected. The results confirm that it is possible to find a model that successfully predicts significant increases in the freight volume. This freight volume-forecasting tool (24 hours ahead) could be used by the different port organizations as a support decision aid for planning resources or facilities. Future work should be aimed at improving the performance of the models in order to provide more accurate predictions of the freight congestion at ports.
Acknowledgements
This work has been partially supported by a grant from the European project FEDER-FSE 2007-2013 and the Fundación Campus Tecnológico Bahía de Algeciras. In addition, the authors thank the Algeciras Bay Port Authority for kindly providing the Ro-Ro traffic database.
References
[1] Chen, M.C. and Wei, Y., Exploring time variants for short-term passenger flow. Journal of Transport Geography, 19(4), pp. 488-498, 2011. DOI: 10.1016/j.jtrangeo.2010.04.003 [ Links ]
[2] Yu, B., Lam, W.H.K. and Tam, M.L., Bus arrival time prediction at bus stop with multiple routes. Transportation Research Part C: Emerging Technologies, 19(6), pp. 1157-1170, 2011. DOI: 10.1016/j.trc.2011.01.003 [ Links ]
[3] Bontekoning, Y.M., Macharis, C. and Trip, J.J., Is a new applied transportation research field emerging?-A review of intermodal rail-truck freight transport literature. Transportation Research Part A: Policy and Practice, 38(1), pp. 1-34, 2004. DOI: 10.1016/j.tra.2003.06.001. [ Links ]
[4] Bianco, L. and La Bella, A., Freight transport planning and logistics: Lucio Bianco and Agostino La Bella: Springer, New York. Computers & Operations Research, 20(5), pp. 562-564, 1993. DOI: 10.1016/0305-0548(93)90047-M. [ Links ]
[5] Zhang, G., Eddy-Patuwo, B. and Y-Hu, M., Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting, 14(1), pp. 35-62, 1998. DOI: 10.1016/S0169-2070(97)00044-7 [ Links ]
[6] Diaz, R., Talley, W. and Tulpule, M., Forecasting empty container volumes. The Asian Journal of Shipping and Logistics, 27(2), pp. 217-236, 2011. DOI: 10.1016/S2092-5212(11)80010-6. [ Links ]
[7] Clark, S.D., Dougherty, M.S. and Kirby, H.R., The use of neural networks and time series models for short term traffic forecasting: A comparative study, Proceedings of PTRC 21st Summer Anual Meeting1993. [ Links ]
[8] Dougherty, M., A review of neural networks applied to transport. Transportation Research Part C: Emerging Technologies, 3(4), pp. 247-260, 1995. DOI: 10.1016/0968-090X(95)00009-8 [ Links ]
[9] Sarmiento, A.T. and Soto, O.C., New product forecasting demand by using neural networks and similar product analysis. DYNA, 81(186), pp. 311-317, 2014. DOI: 10.15446/dyna.v81n186.45223 [ Links ]
[10] Bishop, C.M., Neural networks for pattern recognition. Oxford university press, 1995. [ Links ]
[11] Ke, G.Y., Li, K.W. and Hipel, K.W., An integrated multiple criteria preference ranking approach to the Canadian west coast port congestion conflict. Expert Systems with Applications, 39(10), pp. 9181-9190, 2012. DOI: 10.1016/j.eswa.2012.02.086. [ Links ]
[12] Fan, L., Wilson, W.W. and Dahl, B., Congestion, port expansion and spatial competition for US container imports. Transportation Research Part E: Logistics and Transportation Review, 48(6), pp. 1121-1136, 2012. DOI: 10.1016/j.tre.2012.04.006. [ Links ]
[13] Peng, W. and Chu, C., A comparison of univariate methods for forecasting container throughput volumes. Mathematical and Computer Modelling, 50(7-8), pp. 1045-1057, 2009. DOI: 10.1016/j.mcm.2009.05.027. [ Links ]
[14] Smith, B.L. and Demetsky, M.J., Short-term traffic flow prediction models-a comparison of neural network and nonparametric regression approaches, Systems, Man, and Cybernetics, 'Humans, Information and Technology', IEEE International Conference On, pp. 1706-1709, 1994. [ Links ]
[15] Vlahogianni, E.I., Golias, J.C. and Karlaftis, M.G., Short-term traffic forecasting: Overview of objectives and methods. Transport Reviews, 24(5), pp. 533-557, 2004. DOI: 10.1080/0144164042000195072 [ Links ]
[16] Moscoso-Lopez, J.A., Ruiz-Aguilar, J.J., Turias, I., Cerbán, M. and Jiménez-Come, M.J., A comparison of forecasting methods for ro-ro traffic: A case study in the strait of Gibraltar, in Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T. and Kacprzyk, J., Eds. Springer International Publishing, 2014, pp. 345-353. DOI: 10.1007/978-3-319-07013-1_33. [ Links ]
[17] Ruiz-Aguilar, J. J., Turias, I. J., and Jiménez-Come, M. J., A two-stage procedure for forecasting freight inspections at Border Inspection Posts using SOMs and support vector regression. International Journal of Production Research, 53(7), pp. 2119-2130, 2015. [ Links ]
[18] Seabrooke, W., Hui, E.C.M., Lam, W.H.K. and Wong, G.K.C., Forecasting cargo growth and regional role of the port of Hong Kong. Cities, 20(1), pp. 51-64, 2003. DOI: 10.1016/S0264-2751(02)00097-5. [ Links ]
[19] Chou, C., Chu, C. and Liang, G., A modified regression model for forecasting the volumes of Taiwan's import containers. Mathematical and Computer Modelling, 47(9-10), pp. 797-807, 2008. DOI: 10.1016/j.mcm.2007.05.005. [ Links ]
[20] Fung, M.K., Forecasting Hong Kong's container throughput: An error-correction model. Journal of Forecasting, 21(1), pp. 69-80, 2002. DOI: 10.1002/for.818 [ Links ]
[21] Klein, A., Forecasting the Antwerp maritime traffic flows using transformations and intervention models. Journal of Forecasting, 15(5), pp. 395-412, 1998. DOI: 10.1002/(SICI)1099-131X(199609)15:5<395::AID-FOR628>3.3.CO;2-Z [ Links ]
[22] Ruiz-Aguilar, J.J., Turias, I.J. and Jiménez-Come, M.J., A novel three-step procedure to forecast the inspection volume. Transportation Research Part C: Emerging Technologies, 56, pp. 393-414, 2015. DOI: 10.1016/j.trc.2015.04.024. [ Links ]
[23] Yang, Z., Chen, G. and Moodie, D.R., Modeling road traffic demand of container consolidation in a Chinese port terminal. Journal of Transportation Engineering, 136(10), pp. 881-886, 2010. DOI: 10.1061/(ASCE)TE.1943-5436.0000152 [ Links ]
[24] Park, D. and Rilett, L.R., Forecasting multiple-period freeway link travel times using modular neural networks. Transportation Research Record: Journal of the Transportation Research Board, 1617, pp. 163-170, 1998. DOI: 10.3141/1617-23 [ Links ]
[25] Karlaftis, M. and Vlahogianni, E., Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transportation Research Part C: Emerging Technologies, 19(3), pp. 387-399, 2011. DOI: 10.1016/j.trc.2010.10.004 [ Links ]
[26] Ruiz-Aguilar, J., Turias, I. and Jiménez-Come, M., Hybrid approaches based on SARIMA and artificial neural networks for inspection time series forecasting. Transportation Research Part E: Logistics and Transportation Review, 67, pp. 1-13, 2014. DOI: 10.1016/j.tre.2014.03.009 [ Links ]
[27] Lam, W.H., Ng, P.L., Seabrooke, W. and Hui, E.C., Forecasts and reliability analysis of port cargo throughput in Hong Kong. Journal of Urban Planning and Development, 130(3), pp. 133-144, 2004. DOI: 10.1061/(ASCE)0733-9488(2004)130:3(133) [ Links ]
[28] Gosasang, V., Chandraprakaikul, W. and Kiattisin, S., A comparison of traditional and neural networks forecasting techniques for container throughput at Bangkok port. The Asian Journal of Shipping and Logistics, 27(3), pp. 463-482, 2011. DOI: 10.1016/S2092-5212(11)80022-2. [ Links ]
[29] Robinson, S. and Polak, J.W., Modeling urban link travel time with inductive loop detector data by using the k-NN method. Transportation Research Record: Journal of the Transportation Research Board, 1935(1), pp. 47-56, 2005. DOI: 10.3141/1935-06 [ Links ]
[30] Bhave, N. and Rao, P., Vehicle engine sound analysis applied to traffic congestion Estimation, Proc. of International Symposium on CMMR and FRSM2011, 2011. [ Links ]
[31] Ćavar, I., Kavran, Z. and Petrović, M., Hybrid approach for urban roads classification based on GPS tracks and road subsegments data. PROMET-Traffic & Transportation, 23(4), pp. 289-296, 2011. DOI: 10.7307/ptt.v23i4.131 [ Links ]
[32] Park, T. and Lee, S., A Bayesian approach for estimating link travel time on urban arterial road network, in Anonymous Computational Science and its Applications-ICCSA 2004, Springer, 2004, pp. 1017-1025. DOI: 10.1007/978-3-540-24707-4_114 [ Links ]
[33] Lee, H., Chowdhury, N.K. and Chang, J., A new travel time prediction method for intelligent transportation systems, Knowledge-Based Intelligent Information and Engineering Systems, pp. 473-483, 2008. DOI: 10.1007/978-3-540-85563-7_61 [ Links ]
[34] Boyles, S., Fajardo, D. and Waller, S.T., Naive bayesian classifier for incident duration prediction, Transportation Research Board 86th Annual Meeting, 2007. [ Links ]
[35] Oh, J., Oh, C., Ritchie, S.G. and Chang, M., Real-time estimation of accident likelihood for safety enhancement. Journal of Transportation Engineering, 131(5), pp. 358-363, 2005. DOI: 10.1061/(ASCE)0733-947X(2005)131:5(358) [ Links ]
[36] Adam, T. and Untaroiu, C.D., Identification of occupant posture using a Bayesian classification methodology to reduce the risk of injury in a collision. Transportation research part C: emerging technologies, 19(6), pp. 1078-1094, 2011. DOI: 10.1016/j.trc.2011.06.006 [ Links ]
[37] Kafai, M. and Bhanu, B., Dynamic Bayesian networks for vehicle classification in video. Industrial Informatics, IEEE Transactions on, 8(1), pp. 100-109, 2012. [ Links ]
[38] Khan, S.I. and Ritchie, S.G., Statistical and neural classifiers to detect traffic operational problems on urban arterials. Transportation Research Part C: Emerging Technologies, 6(5), pp. 291-314, 1998. DOI: 10.1016/S0968-090X(99)00005-4 [ Links ]
[39] Abdulhai, B. and Ritchie, S.G., Enhancing the universality and transferability of freeway incident detection using a Bayesian-based neural network. Transportation Research Part C: Emerging Technologies, 7(5), pp. 261-280, 1999. DOI: 0.1016/S0968-090X(99)00022-4 [ Links ]
[40] Abdel-Aty, M. and Pande, A., Identifying crash propensity using specific traffic speed conditions. Journal of Safety Research, 36(1), pp. 97-108, 2005. [ Links ]
[41] Wu, W., Qi-Sen, Z. and Mingjun, W., A method of vehicle classification using models and neural networks, Vehicular Technology Conference, 2001. VTC 2001, Spring. IEEE VTS 53rd, pp. 3022-3026, 2001. [ Links ]
[42] Duda, R.O., Hart, P.E. and Stork, D.G., Pattern Classification. New York: John Wiley & Sons, 2001. [ Links ]
[43] Ripley, B.D., Statistical ideas for selecting network architectures, in Anonymous Neural Networks: Artificial Intelligence and Industrial ApplicationsSpringer, 1995, pp. 183-190. [ Links ]
[44] Keinosuke, F.. Introduction to Statistical Pattern Recognition Academic Press, 1990. [ Links ]
[45] Tinsley, H.E. and Brown, S.D., Handbook of Applied Multivariate Statistics and Mathematical Modeling, Academic Press, 2000. [ Links ]
[46] Bishop, C.M., Pattern Recognition and Machine, Learning Springer New York, 2006. [ Links ]
[47] Rumelhart, D.E., Hinton, G.E. and Williams, R.J., Learning internal representations by error propagation, in Rumelhart, D.E. and McClelland, J.L., Eds. Parallel Distributed Processing Cambridge, MA: MIT Press, 1986, pp. 318-362. [ Links ]
[48] Hornik, K., Stinchcombe, M. and White, H., Multilayer feedforward networks are universal approximators. Neural Networks, 2(5), pp. 359-366, 1989. DOI: 10.1016/0893-6080(89)90020-8 [ Links ]
[49] Zhang, G.P., Neural networks for classification: A survey. Systems, Man and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on, 30(4), pp. 451-462, 2000. DOI: 10.1109/5326.897072. [ Links ]
[50] Kotsiantis, S.B., Zaharakis, I.D. and Pintelas, P.E., Machine learning: A review of classification and combining techniques. Artificial Intelligence Review, 26(3), pp. 159-190, 2006. DOI: 10.1007/s10462-007-9052-3. [ Links ]
[51] Fletcher, R., Practical Methods of Optimization, 2nd Ed. New York: Wiley, 1987. [ Links ]
[52] Hagan, M.T. and Menhaj, M.B., Training feedforward networks with the Marquardt algorithm. Neural Networks, IEEE Transactions on, 5(6), pp. 989-993, 1994. [ Links ]
[53] Friedman, M., The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association, 32(200), pp. 675-701, 1937. DOI: 10.1080/01621459.1937.10503522 [ Links ]
[54] Friedman, M., A comparison of alternative tests of significance for the problem of m rankings. The Annals of Mathematical Statistics, 11(1), pp. 86-92, 1940. DOI: 10.1214/aoms/1177731944 [ Links ]
[55] Salzberg, S.L., On comparing classifiers: Pitfalls to avoid and a recommended approach. Data mining and knowledge discovery, 1(3), pp. 317-328, 1997. DOI: 10.1023/A:1009752403260 [ Links ]
[56] Pizarro, J., Guerrero, E. and Galindo, P.L., Multiple comparison procedures applied to model selection. Neurocomputing, 48(1-4), pp. 155-173, 2002. DOI: 10.1016/S0925-2312(01)00653-1. [ Links ]
[57] Turias, I.J., Gutiérrez, J.M. and Galindo, P.L., Modelling the effective thermal conductivity of an unidirectional composite by the use of artificial neural networks. Composites Science and Technology, 65(3), pp. 609-619, 2005. DOI: 10.1016/j.compscitech.2004.09.018 [ Links ]
[58] Martin, M., Turias, I., Gonzalez, F., Galindo, P., Trujillo, F., Puntonet, C. and Gorriz, J., Prediction of CO maximum ground level concentrations in the Bay of Algeciras, Spain using artificial neural networks. Chemosphere, 70(7), pp. 1190-1195, 2008. DOI: 10.1016/j.chemosphere.2007.08.039 [ Links ]
[59] Fisher, R.A., Statistical methods and scientific inference (2nd Ed.). Hafner Publishing Co., New York, 1959. [ Links ]
[60] Tukey, J.W., Comparing individual means in the analysis of variance. Biometrics, 5(2), pp. 99-114, 1949. DOI: 10.2307/3001913 [ Links ]
[61] Carmer, S.G. and Swanson, M.R., An evaluation of ten pairwise multiple comparison procedures by Monte Carlo methods. Journal of the American Statistical Association, 68(341), pp. 66-74, 1973. DOI: 10.1080/01621459.1973.10481335 [ Links ]
[62] Dietterich, T.G., Approximate statistical tests for comparing supervised classification learning algorithms. Neural Computation, 10(7), pp. 1895-1923, 1998. DOI: 10.1162/089976698300017197 [ Links ]
[63] Ruiz-Aguilar, J.J., Turias, I.J., Jiménez-Come, M.J. and Cerbán, M.M., Hybrid approaches of support vector regression and SARIMA models to forecast the inspections volume. Hybrid Artificial Intelligence Systems, pp. 502, 2014. DOI: 10.1007/978-3-319-07617-1_44 [ Links ]
J.J. Ruiz-Aguilar, received his BSc. Eng. in Civil Engineering in 2006, his MSc. in Civil Engineering in 2008, MSc. in Computational Modeling in Engineering in 2010 and MSc. in Logistics and Port Management in 2012, and his PhD in Civil Engineering in 2014. From 2009 to 2010 he worked for consulting companies in the civil sector and since 2010 has worked for the University of Cádiz, Spain. He is currently a lecturer in the Department of Industrial Engineering and Civil Engineering at the Engineering School of Algeciras, and he is the coordinator of the Port Engineering section of the MSc in Logistics and Port Management, University of Cádiz, Spain. His present interests lie in the field of soft computing, simulation, modeling, forecasting and its applications in civil and logistics problems. ORCID: 0000-0002-2170-0693
I.J. Turias, received his BSc. and MSc. in Computer Science from the University of Málaga, Spain, and his PhD. in Industrial Engineering in 2003 from the University of Cádiz, Spain. He is currently a professor (reader or associate professor) in the Department of Computer Engineering at the University of Cádiz, Spain. His present interests lie in the field of soft computing and its applications in industrial, environmental and logistics problems. He has coauthored numerous technical journals and conference papers, which are the result of his participation and leadership in research projects. He has also served as peer reviewer of several journals and conference proceedings. He has been contracted by a number of companies. He also was the Head of the Engineering School of Algeciras from 2003 to 2011. He is currently the principal researcher of the research group of Intelligent Modeling of Systems. ORCID: 0000-0003-4627-0252
J.A. Moscoso-López, received his BSc. Eng. in Civil Engineering in 2001 and his PhD. in Engineering in 2013 from the University of Cádiz, Spain and his MSc. in Civil Engineering in 2003 from the Alfonso X el Sabio University, Spain. From 2003 to 2009, he worked for civil construction and consulting companies within the civil engineering (construction) sector, and from 2009 he has worked for the University of Cádiz, Spain. He is currently a lecturer in the Department of Industrial Engineering and Civil Engineering at the Engineering School of Algeciras. His research interests include simulation, modeling and forecasting nonlinear time-series in ports and logistics environments. ORCID: 0000-0002-0080-0572
M.J. Jiménez-Come, after completing her BSc. in Chemical Engineering in 2007, from the University of Malaga, Spain, she obtained a PhD. in Engineering and Architecture Programing in 2013, from the University of Cadiz, Spain. Since 2010, she has been working at Cadiz University, Spain, where she is currently a lecturer in the department of Civil and Industrial Engineering. She is a Postdoctoral researcher in the Intelligent Modeling of Systems Research Group. Her research interests include modeling and simulation of industrial process using statistical and computational intelligence techniques. ORCID: 0000-0003-0598-2544
M. Cerbán, obtained a BSc. of Economics in 1994 from the University of Seville, Spain and a PhD in Economics in 2006, from University of Cadiz, Spain. She has been a lecturer of applied economics at the University of Cadiz since 1998, since 1999 she has Director of the MSc. in Logistics and Port Management at the University of Cadiz, Spain and Co-Director of the Interuniversity Master in Port Management and Intermodality at the Universities of Cadiz, La Coruña, Oviedo, Politécnica de Madrid and Puertos del Estado since 2011. Her areas of research include Port Economics, Maritime Transports and Logistics. ORCID: 0000-0003-4674-0453