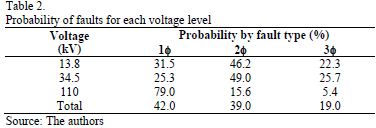Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.195 Medellín jan./fev. 2016
https://doi.org/10.15446/dyna.v83n195.49495
DOI: http://dx.doi.org/10.15446/dyna.v83n195.49495
Voltage sag assessment using an extended fault positions method and Monte Carlo simulation
Evaluación de hundimientos de tensión mediante un método extendido de posiciones de falla y simulación de Monte Carlo
Jorge W. Sagre a, John E. Candelo b & Johny H. Montaña c
a Grupo de Investigación en Sistemas Eléctricos de Potencia, Universidad del Norte, Barranquilla, Colombia. jsagre@uninorte.edu.co
b Departamento de Energía Eléctrica y Automática, Universidad Nacional de Colombia, Medellín, Colombia. jecandelob@unal.edu.co
c Departamento de Ingeniería Eléctrica, Universidad Técnica Federico Santa María, Valparaíso, Chile. johny.montana@usm.cl
Received: March 5th, 2015. Received in revised form: August 4rd, 2015. Accepted: August 19th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
In this article, we propose an extended fault positions method combined with the Monte Carlo method to evaluate voltage sags. The distribution function SARFI is obtained by taking into account the randomness of (i) location of faults in lines, (ii) generation dispatch, and (iii) the prefault voltage. Voltage magnitudes are calculated with power flow, while noting changes in the generation dispatch, the load, and the topology of the area of vulnerability (AOV). The method is tested in the Atlantic coast area of the National Interconnected Power System of Colombia. The distribution of the number of voltage sags per year with the magnitude in bus bars and the impact of generation on the voltage sags are determined. With a higher number of plants dispatched, voltage sags caused by faults are less severe due to the robustness of the power system and the voltage support. Operation with coupled bars had a greater impact on voltage sags compared to uncoupled bars.
Keywords: electromagnetic compatibility; fault position method; Monte Carlo; power quality; voltage sags.
Resumen
En este artículo, proponemos un método extendido de posición de falla combinado con el método de Monte Carlo para evaluar los hundimientos de tensión. La función de distribución SARFI se obtiene teniendo en cuenta la aleatoriedad de (i) los puntos de fallas en las líneas (ii) el despacho de generación y (iii) la tensión prefalla. Las magnitudes de tensión se calcularon con flujos de carga, considerando cambios en la generación, la carga y la topológica del área de vulnerabilidad (AOV). El método se probó en el área de la Costa Atlántica perteneciente al Sistema Eléctrico Interconectado Nacional de Colombia. Se calculó la distribución del número de hundimientos de tensión por año, con la magnitud en barras y el impacto de la generación de los hundimientos de tensión. Cuando se despacha un número mayor de plantas, los hundimientos de tensión causados por fallas fueron menos graves, debido a la robustez del sistema de alimentación y el soporte de tensión. La operación con las barras acopladas trae mayor impacto en los hundimientos de tensión comparada con las barras desacopladas.
Palabras clave: compatibilidad electromagnética; método de posición de falla; Monte Carlo; calidad de potencia; hundimientos de tensión.
1. Introduction
Users' requirements for better power quality have increased in the last three decades. One of the reasons is the economic impact of voltage sags in the power grid on customers and end-use equipment manufacturers [1,2].
Several factors affect power quality [1,3-5]: devices powered by electronic converters, speed drivers, and compact fluorescent lamps (CFL). Furthermore, distributed generation and renewable energy sources can create voltage variations, flickers, and harmonic distortion. Similarly, energy efficiency equipment is an important source of disturbance. All these devices are very sensitive to voltage sags because they are manufactured with narrow ranges of operation for competitive reasons [5].
Many power quality studies have been conducted and reported on previously, including (i) measurement techniques, (ii) evaluation of voltage sags, and (iii) the economic impacts of equipment damage and losses in industrial processes.
In [6], the application of probabilistic methods was presented to predict and characterize how often events appear in the power system in order to assess their impact, demonstrating how a user can be affected.
In [7], the impact of the fault probability distribution model of transmission lines in assessing the number of voltage sags and their characteristics was analyzed.
In [8], the behavior of voltage sags using fault positions and the Monte Carlo method was evaluated. The results showed that the Monte Carlo method provides a better statistical description of voltage sags compared to the fault positions method, which offers only long-term average values, whereas Monte Carlo shows the total distribution function.
In [9], the fault positions method and a Monte Carlo simulation were compared in order to stochastically evaluate voltage sag behavior in a large transmission system. This work showed that the fault positions method cannot be used to predict the behavior of a particular year unless correction factors are used to adjust the behavior. Whereas the fault positions method gives average values, the Monte Carlo method describes the complete frequency distribution function of the voltage sags index (SARFIX: System Average RMS Frequency Index; average number of voltage sags per year with magnitude < X%).
In [10], the Monte Carlo method and the fault positions method were applied to evaluate voltage sag indices. This approach assesses the randomness of the prefault conditions and uncertainty in failure rates.
In [11], a method for stochastic prediction of voltage sags generated by faults in the power system was presented. Furthermore, a method for determining the AOV was proposed.
In [12], the influence of generation dispatch and failure rates changing over time on the stochastic prediction of voltage sags was discussed.
In [13], the fault positions method was presented to stochastically predict the frequency and characteristics of balanced and unbalanced voltage sags in distribution systems.
In [14], an analytical method for the stochastic prediction of voltage sags in high-voltage networks was proposed. The method is based on the Z matrix and was applied to the IEEE 24-node reliability test system.
In [15], an evaluation of voltage sags based on the concept of area of severity (AOS) and the impact rankings of the lines and buses was presented. These concepts are useful for creating an efficient plan for mitigating voltage sags and evaluating the relationship between sensitive load points and system voltage sag performance.
In [16], a methodology to estimate the magnitude and frequency of voltage sags originating from faults was presented. The method took into account the application of statistical analysis such as the confidence interval and analysis of variance.
The fault positions and Monte Carlo methods have provided good results in evaluating the impact of generation on voltage sags and SARFI indices. Unfortunately, the behavior of generation dispatch is not randomized and the voltage profiles in the faulted bus bar and the bus bar of interest are considered to be constant parameters.
In this paper, an extended fault positions technique and the Monte Carlo method are proposed to evaluate voltage sags. Random faults, changes in generation dispatch, and load variation were taken into account in order to evaluate different operating conditions. The voltage profiles in bus bars were updated continuously using the power flow. Topology changes related to bus bars and transmission lines were also included in the simulation. Although voltage sags can be caused by lightning, disconnection of large loads, etc., this work focuses only on faults in bus bars and the overhead lines of the power system.
2. Theoretical background
2.1. Voltage sags
A voltage sag is "a decrease in r.m.s. voltage or current at the power frequency for durations of 0.5 cycle to 1 min. Typical values are 0.1 to 0.9 p.u." [17]. They are caused by events with large current flows through the network as a result of a fault at any point in the distribution or transmission network, and they affect customers [3,8,9,18].
Events that can cause voltage sags are short circuits, transformer energization, capacitor disconnection, large motors starting, and large load changes in the power system [18]. Consequences include equipment shutdown, process disruption, damage to or malfunction of electronic controllers, slight reduction in output from a capacitor bank, changes in torque and speed of induction motors [18], and others.
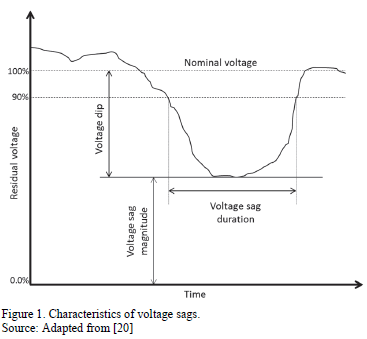
Voltage sag is characterized mainly by means of magnitude and duration [1,3,4,19], as shown in Fig. 1. Additionally, voltage sag can be characterized by the frequency of occurrence, phase shifting, the start point in the voltage waveform, and the shape and type of voltage sag.
Standard IEC 61000-4-30 [21] presents a calculation of a sliding reference voltage using a first-order filter for 1 minute. The filter is given by the expression presented in (1).
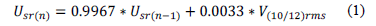
where Usr(n) is the actual value of the sliding reference voltage, Usr(n-1) is the previous value of the sliding reference voltage, and V(10/12)rms is the most recent 10/12 cycle r.m.s. value.
Vrms(1/2) is computed from the voltage samples in the time domain, as shown in (2) [2,4,7].
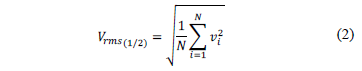
where i corresponds to each sample, N is the total number of samples, and vi is the voltage value in the time domain. The value is updated every half cycle.
Most measurement devices use the lower value of Vrms(1/2) computed each half cycle in the time domain as the voltage sag magnitude [3].
2.2. Fault positions method
The fault positions method is a stochastic method that predicts the expected number of voltage sags in a specific node of the network. In this method, faults in different places on the network are taken into account. Electrical variables for each fault are stored: residual voltage and fault duration on the nodes of interest, as shown in Table 1.
A failure rate is assigned to each fault position. The transmission lines are divided into a specific number of fixed positions. Each position has a failure rate, which is proportional to the longitude of each section. Thus frequency, magnitude, and duration are determined for each fault position, allowing us to calculate the expected number of voltage sags per year [8,9,11,13,14].
Unlike the conventional fault positions method, the fault positions are fixed; in the proposed method in this work, the positions are randomly assigned anywhere in the transmission line for each type of fault.
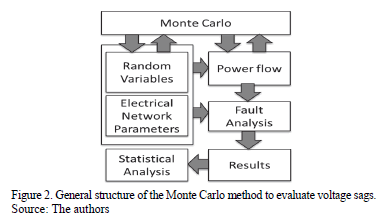
2.3. Monte Carlo method
The Monte Carlo method is used to simulate the distribution function of the expected values of voltage sags (SARFIx). This method generates the stochastic variables associated with this study, as shown in Fig. 2 [8,9].
The following steps are part of the algorithm to implement the Monte Carlo method [8,9].
- Select the observation node.
- Select the years of simulation.
- For elements in the area of vulnerability, generate a random number to define the fault time according to the probability distribution of the failure rate.
- Compute the accumulated time.
- Generate a random number to define a position over the transmission line according to the probability distribution of this parameter.
- For each fault, generate a random number to define one fault type (SLG, LL, LLG, LLL) according to the probability distribution function of the fault type.
- Compute the residual voltage as a result of the fault in the observation node.
- If the accumulated time is less than the simulation time selected, go to step 3. Otherwise go to step 9.
- Analyze the results statistically.
3. Methodology
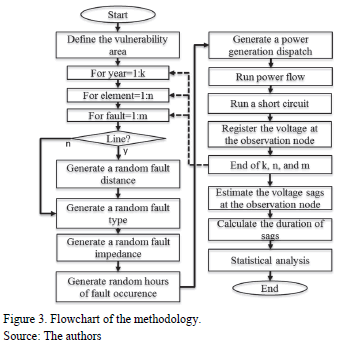
This work was done using the fault positions method combined with the Monte Carlo simulation method. Fig. 3 shows the flowchart used to study the voltage sags in a power system.
4. Analytical procedure
4.1. Statistical analysis of results
The great volume of data generated by the Monte Carlo analysis has to be summarized by means of statistical tools. The most important results from Monte Carlo are the long-term mean values and the frequency distribution of mean values [3,8,9,16].
Calculation of the mean values and standard deviation of the voltage sags lower than the predefined magnitudes must be carried out. Their magnitudes are commonly defined between 0.1 and 0.9 in steps of 0.1. It is also important to calculate minimum, maximum, median, and quartiles 1, 2, and 3.
Once the deviation, mean value 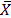 , and standard deviation s are known, the confidence intervals for the expected value can be obtained as expressed in (3) [8,9,16].
, and standard deviation s are known, the confidence intervals for the expected value can be obtained as expressed in (3) [8,9,16].
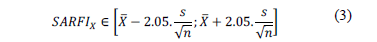
where 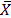 is the mean value of voltage sags per year, s is the standard deviation, n is the number of years of simulation, and the constant 2.05 is the critical value of t-student distribution for 95% confidence.
is the mean value of voltage sags per year, s is the standard deviation, n is the number of years of simulation, and the constant 2.05 is the critical value of t-student distribution for 95% confidence.
4.2. Area of vulnerability (AOV)
The area of vulnerability was identified by means of power system analysis software that takes fault analysis into account. Faults were simulated at each node of the network, considering the worst cases:
- Three-phase fault solidly grounded (Rf=0)
- Minimum generation dispatch
- Time of maximum demand
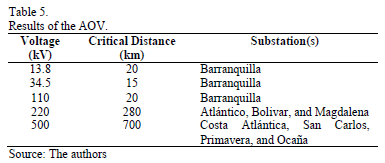
Faults were simulated sequentially by voltage level, recording the residual voltage in the node under study and the electrical distance between the node and fault point for each fault. Thus, the maximum distance was obtained for each voltage level for which the residual voltage was lower than 0.9 p.u. (critical distance).
4.3. Simulation time
According to records of meters installed in the node under study, the number of voltage sags per year was between 250 and 340. Thus, given 360 voltage sags per year and an expected error lower than 2% for a confidence of 95%, the minimum number of years to be considered in the simulation was 25.
4.4. Stochastic factors
Five factors were taken into account in the simulations in order to evaluate their impact on the voltage sags in the network.
4.4.1. Resistance
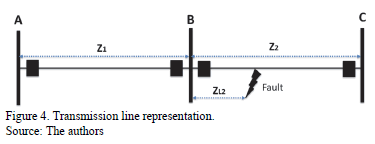
The resistance values were modeled stochastically with normal distribution and standard deviation equal to 1 [22]. The mean value of the resistance was obtained from records of phase-ground faults recorded by distance protection relays.
Historical data was used to obtain at least 20 events of voltage and the current waveform of phase-ground failures registered by a distance relay. Based on these waveforms, the fault current was calculated by
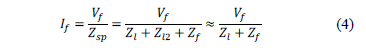
where
Vf = Fault voltage
If = Fault current
Zsp = Impedance from source up to fault point
Zl =Impedance of transmission line A - B (Fig. 4)
Therefore, Zf can be obtained from the above equation as expressed in (5):
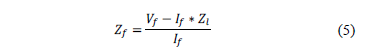
The mean value of fault impedance is the average value of fault impedances estimated by means of equation (5).
4.4.2. Type of fault
The type of fault was obtained randomly from the probability distribution of faults at each voltage level. This probability was computed from the voltage sag data measured at each bus bar. Table 2 shows the probabilities of different faults at each voltage level of the network under study.
For each voltage level, the voltage sags were classified as 1 phase, 2 phases, and 3 phases. The probability of presenting each event was calculated as a percentage from the total events of each voltage level.
4.4.3. Fault position in transmission lines
Many methods in the literature use a constant number of segments for dividing the transmission line; therefore, each segment has a fixed failure rate. In this work, the transmission line was not divided into segments, but the fault position was computed by means of a random number generated from the probability distribution. This random number was multiplied for the length of the overhead line, and the fault position was obtained.
4.4.4. Time period of the faults
The time of occurrence of a fault was obtained by means of a random number generated between 0 and 23. The number 0 means the time from 00:00 to 01:00, the number 1 means the time from 01:00 to 02:00, and so on. The demand of each node in the network and the prefault voltage were computed from the randomly generated time of occurrence and the load profile at each bus bar by means of a power flow.
4.4.5. Generation dispatch
Generation dispatch was also generated randomly from the probability distribution. In this study, the generation dispatch had two options: (1) all generation plants dispatched and (2) operation without generation plants connected to 110 kV bus bars. The voltage sag analysis was developed in a real power system where four generation scenarios were taken into account:
- Baseline scenario: 30% of the time, all generators are dispatched. This is typical behavior during the dry season in Colombia (4 months).
- Scenario 2: 40% of the time, all generators are dispatched. This occurs when the dry season is a little bit longer (5 months).
- Scenario 3: 60% of the time, all generators are dispatched. Dry season is even longer (7 months).
- Scenario 4: 70% of the time, all generators are dispatched. This scenario occurs during the "El Niño" phenomenon, when the dry season is even longer (8 months).
4.5. Definition of dynamic variables
The load profile at each bus bar of the network was simulated as a dynamic variable. Additionally, the failure rate of transmission lines and substations of the AOV were considered to be dynamic events.
For the failure rate, it was assumed that the time between the fault at the bus bar and the substation of the power system followed an exponential distribution. The failure rate of elements in the AOV was calculated from the real statistics of the power system under study.
4.6. Validation of the model
Validation of the model was done by comparing the records from 3 years in which the expected average number of voltage sags were found with simulations covering a longer period (25 years) [13].
The expected voltage sags were determined by the confidence intervals from the results of the simulation at the points of interest. To estimate the confidence intervals, the method of percentiles was used regardless of the probability distribution [16].
4.7. Voltage sag duration
Theoretically, the best way to calculate the duration of each voltage sag is to know the clearance time of the fault. Therefore, knowledge of the fault currents, protection relay settings, and breaker times is needed. Obtaining all the information from distribution networks is sometimes a difficult assignment because of the amount of data required to continuously update the databases. Based on [23], in this research a random generation of voltage sag duration was implemented, which took into account the distribution probability of voltage sag durations registered by measurement devices at the bus bars.
5. Power system under study
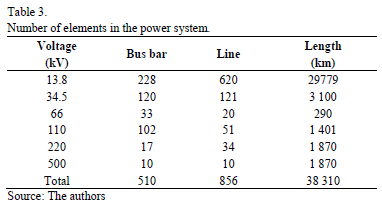
The Atlantic coast area of the National Interconnected Power System of Colombia was used to test the proposed method. General information about this power system is presented in Table 3.
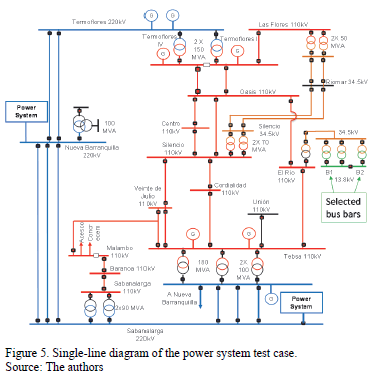
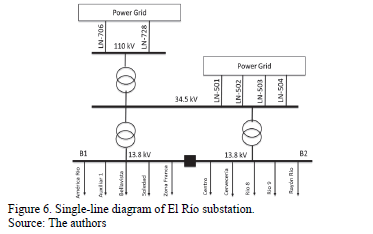
Fig. 5 shows a single-line diagram of the Atlantic coast area of the National Interconnected Power System of Colombia, which was used for power quality studies.
The aim of the simulation was to characterize the behavior of the power system using the number of voltage sags as a function of the magnitude and duration at a preselected point. The selected points were bus bars B1 and B2 at 13.8 kV of the El Río substation in coupled and uncoupled configurations. These bus bars can be coupled and uncoupled by a circuit breaker.
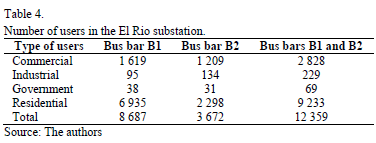
This study stochastically analyzed the behavior of the voltage sags at a bus bar with users connected. Table 4 shows information about the number of users connected to the bus bar. The simulation considered 8687 users connected to bus bar B1, 3672 users connected to bus bar B2, and 12 359 users connected to the coupled bus bars.
6. Results and analysis
6.1. Area of vulnerability
Fig. 6 shows a single-line diagram of the power system used to carry out the studies. The AOV for the selected bus bars was calculated using three-phase faults at each bus bar to evaluate the voltage magnitudes.
Based on methodology previously described, the AOV was calculated for fault impedance equal to zero with a minimum number of generation plants and maximum demand. Table 5 presents a summary of the critical distances for different voltage levels.
6.2. Power quality indices
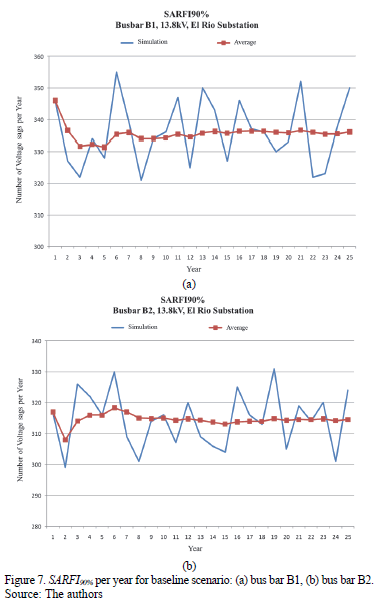
Fig. 7 shows the behavior of the Monte Carlo simulation for bus bars B1 and B2 respectively. Fig. 7a and Fig. 7b show the SARFI90% per year of simulation and the behavior of the voltage sags in bus bars B1 and B2 of the El Rio substation. The index SARFI90% changes for the first few years but becomes stable after the eighth year.
6.3. Distribution of voltage sags
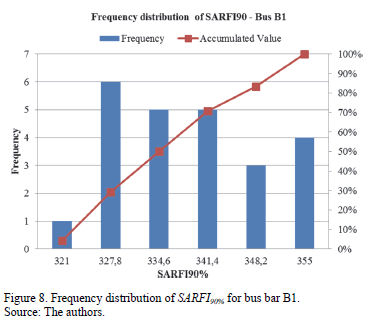
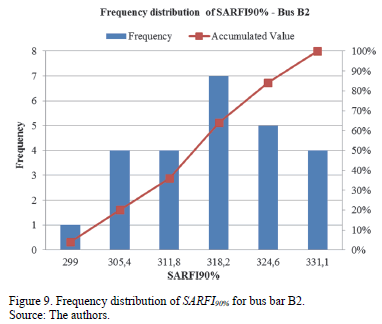
Fig. 8 and Fig. 9 show the frequency distribution of SARFI90% for bus bars B1 and B2 respectively.
These figures show the differences between frequencies of the SARFIx index of bus bars B1 and B2 for the simulated scenarios. Most of the annual voltage sags for bus bar B2 are lower than those for bus bar B1, which helps identify the best configurations for the electrical network.
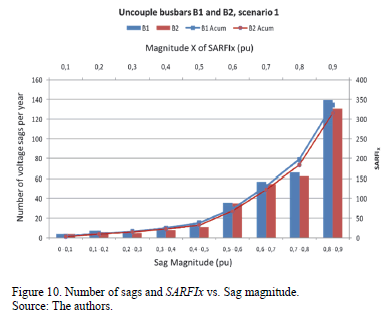
Fig. 10 shows the expected number of sags per year and the SARFIx for ranges between 0% and 90% for bus bars B1 and B2 of the El Rio substation.
6.4. Results of the model
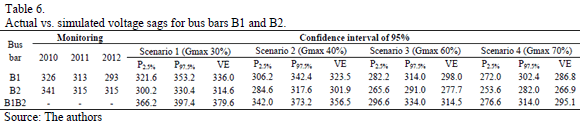
Table 6 shows the number of actual voltage sags versus the number of voltage sags simulated for bus bars B1 and B2. The measurements of the actual voltage sags were carried out for the years 2010, 2011, and 2012. The results of the Monte Carlo simulation were obtained according to the four generation dispatch scenarios defined in the methodology.
In the long term, the expected number of voltage sags with magnitude £ 90% (SARFI90%) was lower for bus bar B2 than for bus bar B1 because the expected value for SARFI90% in bus bar B2 was less than the corresponding percentile P2.5% for all scenarios.
Comparing the results of the Monte Carlo simulation for both scenarios-coupled and uncoupled bus bars-and utilizing the same failure rate of the elements in the AOV, the results show that the coupled bus bars generated a higher number of voltage sags than the uncoupled bus bars. If the number of generation plants were to increase, the problem would become less detectable.
With the exception of bus bar B2 for the year 2010, the expected values of voltage sags for B1 and B2 were contained in the corresponding confidence intervals for the two scenarios considered, compared to measurements.
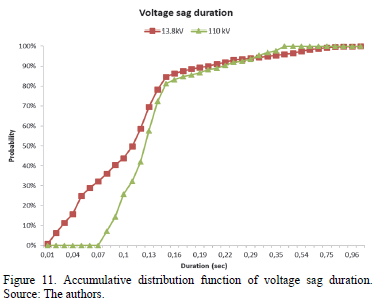
6.5. Voltage sag duration
The probability distribution of voltage sag duration is shown in Fig. 11, calculated for 13.8 kV and 110 kV. These results were obtained by combining the magnitude and duration of the voltage sags.
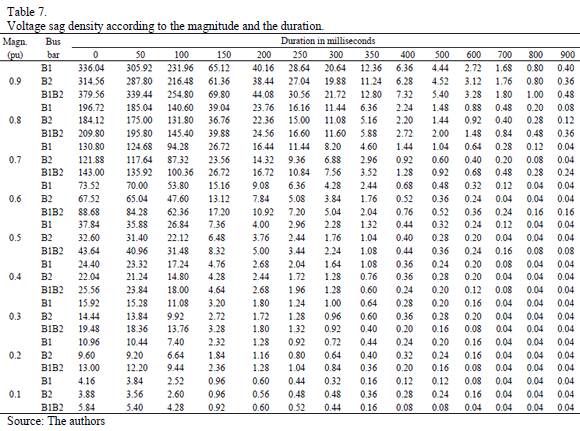
Table 7 shows the accumulated voltage sags for the coupled and uncoupled bus bars B1 and B2. The voltage sag magnitudes with the coupled bus bars B1 and B2 are similar to the voltage sag magnitudes obtained with the uncoupled bus bars. The number of voltage sags is greater with the coupled bus bars.
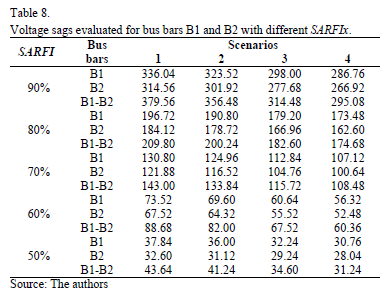
Table 8 shows the accumulated voltage sags for different percentages of SARFI. The information is presented for the coupled and uncoupled bus bars B1 and B2.
For all SARFI studied, the number of accumulated voltage sags was greater for bus bar B1 than for bus bar B2. Furthermore, the coupled bus bars presented a greater number of voltage sags for all scenarios studied.
7. Conclusions
This paper presented an extended fault positions method combined with the Monte Carlo method to evaluate the impact of voltage sags in a power system. Random faults in transmission lines, variation of generation dispatch, and variations of load were taken into account for the simulations. Statistical tests were conducted, finding that the greater the number of generation plants dispatched in the AOV, the lower the magnitude of the voltage sags and the index SARFI. The proposed method evaluated the reconfiguration of bus bars to reduce the number of voltage sags, finding that coupled bars have a greater impact on voltage sags compared to the results obtained with uncoupled bars. The results showed that voltage sags have a significant impact on power system operation. The parameters and the method utilized in this research should be included in any future power quality analysis.
Acknowledgements
This research was supported in part by the Universidad del Norte - Colombia, the Universidad Nacional de Colombia - Sede Medellín - Colombia, and the Universidad Técnica Federico Santa María - Chile. The authors wish to thank the company ELECTRICARIBE for the valuable information provided for this research.
References
[1] Dugan, R.C., McGranaghan, M.F., Santoso, S. and Beaty, H.W., Electrical Power Systems Quality. Third. McGraw-Hill Education, 2012. [ Links ]
[2] Gil-Montoya, F., Manzano-Agugliaro, F., Gómez-López, J. and Sánchez-Alguacil, P., Técnicas de investigación en calidad eléctrica: ventajas e inconvenientes. DYNA, 79(173), pp. 6-74, 2012. [ Links ]
[3] Bollen, M., Understanding power quality problems: Voltage sags and interruptions. New Jersey: Wiley-IEEE Press, 1999. DOI: 10.1109/9780470546840 [ Links ]
[4] Bollen, M. and Gu, I., Signal processing of power quality disturbances. New Jersey: Wiley-IEEE Press, 2006. DOI: 10.1002/9780471931317 [ Links ]
[5] Giménez-Álvarez, J. y Gómez-Targarona, J., Generación eólica empleando distintos tipos de generadores considerando su impacto en el sistema de potencia. DYNA, 78(169), pp. 95-104, 2011. [ Links ]
[6] Sikes, D.L., Comparison between power quality monitoring results and predicted stochastic assessment voltage sags-"real" reliability for the customer. IEEE Transactions on Industry Applications, 36(2), pp. 677-82, 2000. DOI: 10.1109/28.833787 [ Links ]
[7] Milanovic, J.V., Aung, M.T. and Gupta, C.P., The influence of fault distribution on stochastic prediction of voltage sags. IEEE Transactions on Power Delivery, 20(1), pp. 278-285, 2005. DOI: 10.1109/TPWRD.2004.835052 [ Links ]
[8] Olguin, G., Aedo, M., Arias, M. and Ortiz, A., A Monte Carlo simulation approach to the method of fault positions for stochastic assessment of voltage dips (sags), IEEE/PES Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005. pp. 1-6. DOI: 10.1109/TDC.2005.1546794 [ Links ]
[9] Olguin, G., Karlsson, D. and Leborgne, R., Stochastic assessment of voltage dips (Sags): The method of fault positions versus a Monte Carlo simulation approach, IEEE Russia Power Tech, 2005. pp. 1-7. DOI: 10.1109/TDC.2005.1546794 [ Links ]
[10] Caramia, P., Carpinelli, G., Di Perna, C., Varilone, P. and Verde, P., Fast probabilistic assessment of voltage dips in power systems, 9th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), 2006. pp. 1-6. DOI: 10.1109/PMAPS.2006.360405 [ Links ]
[11] Park, C.-H. and Jang, G., Stochastic estimation of voltage sags in a large meshed network. IEEE Transactions on Power Delivery, 22(3), pp. 1655-1664, 2007. DOI: 10.1109/TPWRD.2006.886795 [ Links ]
[12] Park, C.-H., Jang, G. and Thomas, R.J., The influence of generator scheduling and time-varying fault rates on voltage sag prediction. IEEE Transactions on Power Delivery, 23(2), pp. 1243-1250, 2008. DOI: 10.1109/TPWRD.2008.915836 [ Links ]
[13] Goswami, A.K., Gupta, C.P. and Singh, G.K., The method of fault position for assessment of voltage sags in distribution systems, IEEE Region 10 and the Third international Conference on Industrial and Information Systems (ICIIS), 2008. pp. 1-6. DOI: 10.1109/ICIINFS.2008.4798362 [ Links ]
[14] Quaia, S. and Tosato, F., A method for analytical voltage sags prediction, IEEE Bologna Power Tech Conference Proceedings, 4, 2003. pp. 181-186. DOI: 10.1109/PTC.2003.1304720 [ Links ]
[15] Park, C.-H., Hong, J.-H. and Jang, G., Assessment of system voltage sag performance based on the concept of area of severity. IET Generation, Transmission and Distribution, 4(6), pp. 683-693, 2010. DOI: 10.1049/iet-gtd.2009.0492 [ Links ]
[16] De Oliveira, T., Carvalho-Filho, J.M., Abreu, J.P. and Chouhy-Leborgne, R., Voltage sags: Statistical evaluation of monitoring results based on predicted stochastic simulation. 12th International Conference on Harmonics and Quality of Power, 2006. [ Links ]
[17] IEEE Std. 1346. Recommended practice for evaluating electric power system compatibility with electronic process equipment. 1998. [ Links ]
[18] Jaramillo-Matta, A.A., Guasch-Pesquer, L. and Trujillo-Rodriguez, C.L., Classification of voltage sags according to the severity of the effects on the induction motor. DYNA, 82(190), pp. 96-104, 2015. DOI: 10.15446/dyna.v82n190.43286 [ Links ]
[19] IEC Std. 61000-2-8 Voltage dips and short interruptions on public electric power supply systems with statistical measurement results. 2002. [ Links ]
[20] IEEE Std. 1159. IEEE recommended practice for monitoring electric power quality. 1995. [ Links ]
[21] IEC Std. 61000-4-30, Testing and measurement techniques-Power quality measurement methods. 2003. [ Links ]
[22] Avendano-Mora, M., Milanović, J.V., Patel, B. and Zhang, Y., The influence of model parameters and uncertainties on assessment of network wide costs of voltage sags, 10th International Conference on Electrical Power Quality and Utilisation (EPQU), 2009. pp. 1-7. DOI: 10.1109/EPQU.2009.5318857 [ Links ]
[23] Wämundsson, M., Calculating voltage dips in power systems, using probability distributions of dip durations and implementation of the moving fault node method, MSc. Thesis, Department of Energy and Environment, Chalmers University of Technology, Göteborg, Sweden, 2007. [ Links ]
J. Sagre, received his BSc. in Electrical Engineering in 1978 from the Universidad Nacional de Colombia, Bogotá, Colombia and a MSc. in Electrical Engineering in 2014 from Universidad del Norte, Barranquilla, Colombia. His employment experiences include: the Corporación Eléctrica de la Costa Atlántica - CORELCA -, TRANSELCA S.A. E.S.P. and ELECTRICARIBE S.A. E.S.P. He is now a Consultant Engineer. His research interests include: planning, operation and control of power systems, power quality and regulation. ORCID: 0000-0001-8036-0644
J. Candelo, received his BSc. in Electrical Engineering in 2002 and his PhD in Engineering with emphasis in Electrical Engineering in 2009 from Universidad del Valle, Cali, Colombia. His employment experiences include the Empresa de Energía del Pacífico EPSA, Universidad del Norte, and Universidad Nacional de Colombia, Medellín, Colombia. He is now an assistant professor of the Universidad Nacional de Colombia, Medellín, Colombia. His research interests include: planning, operation and control of power systems, artificial intelligence and smart grids. ORCID: 0000-0002-9784-9494
J. Montaña, received his BSc. in Electrical Engineer, MSc. in High Voltage, and his PhD. in 1999, 2002, and 2006, all of them from Universidad Nacional de Colombia,. He is a full-time professor with the Department of Electrical Engineering, Universidad Federico Santa María, Valparaiso, Chile. He worked as a research assistant with Universidad Nacional de Colombia from 2000 to 2005, as junior design engineer with Siemens S.A. Colombia, from 2006 to 2009, and a fulltime professor with Universidad del Norte, Barranquilla, Colombia, from 2010 to 2013. His research interests include lightning protection systems, lightning location systems, and grounding systems. ORCID: 0000-0002-9999-2366