DOI: http://dx.doi.org/10.15446/dyna.v83n195.51138

Evaluation of internal and external stresses on the SPT sampler

Evaluación de las tensiones internas y externas que actúan sobre el muestreador del ensayo SPT

 

Juliana Zapata-Galvis ^a & Edmundo Rogério-Esquivel ^b

 

^a Departamento de Geotecnia, Escola de Engenharia de São Carlos- Universidade de São Paulo, São Carlos, Brasil. julyszapata44@hotmail.com
^b Departamento de Geotecnia, Escola de Engenharia de São Carlos- Universidade de São Paulo, São Carlos, Brasil. esquiveleesc@gmail.com

 

Received: June 9^th, 2015. Received in revised form: September 11^th, 2015. Accepted: September 21^th, 2015.

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
The N_SPT index is usually used in empirical correlations to estimate parameters of the soil, carrying capacity, foundation settlement, etc. Because these correlations have no scientific basis, researchers have been developing rational methods of analysis, based on energy concepts. The amounts of energy involved in the SPT test are evaluated by the EFV method. With force and acceleration records, amounts of energy, equipment efficiency, experimental dynamic reaction force of the soil and stresses acting on the sampler were assessed. In this study, a sample extractor system was designed, which consists of a base, a hydraulic cylinder and a load cell. The objective of this equipment is to experimentally quantify the internal friction force, allowing the stresses acting on the sampler to be evaluated. Also, the Aoki's a parameter, which is the ratio of internal friction and external friction between the ground and the sampler, could be calculated.

Keywords: SPT test; energy; efficiency; stress on the sampler; dynamic instrumentation; Aoki's a parameter.

Resumen
El índice N_SPT es muy utilizado en correlaciones empíricas para estimar parámetros del suelo, capacidad de carga, asentamiento de fundaciones, etc. Debido a que estas correlaciones no tienen ningún fundamento científico, investigadores han desarrollado métodos racionales de análisis, basados en conceptos de energía. La cantidad de energía envuelta en el ensayo SPT es evaluada por el método EFV. Con los registros de fuerza y aceleración, pueden ser obtenidas las cantidades de energía presentes en el ensayo SPT, la eficiencia del equipo, la fuerza de reacción dinámica experimental del suelo y las tensiones que actúan sobre la cuchara partida. En este estudio, se diseñó un sistema de extracción de muestras, el cual se compone de una base, un cilindro hidráulico y una célula de carga. El objetivo de este equipo es cuantificar experimentalmente la fuerza de fricción interna, lo que permite determinar las demás fuerzas y tensiones que actúan sobre la cuchara partida. Además, se puede calcular el parámetro a de Aoki que es la relación de la fricción interna y externa entre el suelo y el muestreador.

Palabras clave: Ensayo SPT; energía; eficiencia; tensiones que actúan en el muestrador; instrumentación dinámica; parámetro a de Aoki.

---

 

1. Introduction

The standard penetration test (SPT) does not directly measure the shear strength of soils. Because of this, different authors have suggested empirical correlations to estimate relative density, friction angle and other soil parameters [1]. However, as these correlations have no scientific basis, researchers have been developing rational methods of analysis that are based on energy concepts.

The SPT (Standard Penetration Test), standardized in Brazil by ABNT-NBR 6484 (2001) [2], is usually used to estimate soil resistance through the dynamic resistance index (N_SPT). This index refers to the number of hammer blows required to penetrate the SPT sampler 0.30 m into the soil after an initial penetration of 0.15 m. The blows are produced by lifting the 65-kg hammer at a height of 0.75 m and dropping it in free fall, transmitting its potential energy (478.2 J) to the string of rods.

However, as this N_SPT index does not directly represent the real value of soil resistance, researchers have developed energy-based methods to estimate the theoretical static reaction force (R_S) and the theoretical dynamic reaction force (F_d) of the soil [3-5]. Both theoretical reactions forces and the experimental dynamic resistance (R_D), mobilized during the penetration of the sampler, are obtained from the energy transferred during the propagation of waves in the string of rods and the sampler.

This paper presents the results of SPT tests conducted in the Experimental Field of the University of Sao Paulo at Sao Carlos. The SPT tests were performed with an instrumented subassembly, which was placed at the base of the string of rods. The amount of energy transmitted to the sampler could be evaluated using measured accelerations and forces, which allowed the equipment efficiency to be calculated.

The accelerations and forces were measured through an instrumented subassembly, which is composed of two accelerometers and a load cell, and placed at the top of the sampler.

The internal friction force between the soil and the internal sampler wall was evaluated using a sample extracting system in order to subsequently assess the other stresses acting on the sampler. Finally, knowing these stresses, the Aoki's a parameter, which is the ratio of internal friction and external friction between the soil and the sampler wall, respectively, can be calculated.

 

2. The sample energy and reactions.

2.1. Energy and efficiency

The amount of energy transferred to the sampler (E_base), can be either theoretically or experimentally estimated. Experimentally, the amount of energy can be evaluated through the EFV method, which consists of the integration of the product of the normal force (F) and velocity (v) with respect to time (eq. 1). The velocities (v) were calculated by integrating acceleration with respect to time.

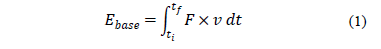
where the t_i is the initial instant corresponding to the beginning of the event, that is, when the force becomes different from zero, and t_f is the final instant, when the force and velocity signals becomes zero and no subsequent impacts occur.

Theoretically, according to Odebrecht [6], the system's potential energy (EP_system) is the theoretical potential energy (EP_i) plus the potential energy of the hammer and rods due to the sampler penetration into the soil (eq. 2).

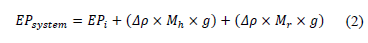
Where,

H = height of fall (m).
Dr= permanent sampler penetration (m).
M_r= rod mass (kg).
M_h= hammer mass (kg).
g= acceleration of gravity (m/s²).

However, the amount of energy that reaches the sampler (E_sampler) is lower than EP_system due to energy losses that occur in the process of penetrating the sampler into the soil [7]. These energy losses depend on the type of equipment (type of hammer, the length of the string of rods, the geometry of the sampler, test procedures, i.e., mechanical or automatic, etc.), loose rod couplings and reflections due to cross section changes.

According to Odebrecht et al. [8], these losses are represented by three distinct coefficients: h₁ (hammer efficiency), h₂ (efficiency of the string of rods) and h₃ (system efficiency). The energy actually reaching the sampler is shown in eq. (3).

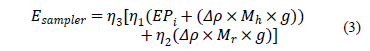
Where,

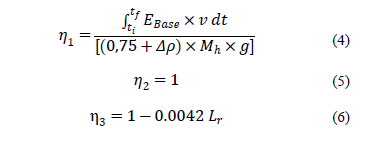
L_r = total length of the string of rods.

The equipment efficiency (h) is the ratio of the energy that reaches the sampler (E_base) and the system's potential energy (EP_system).

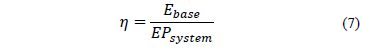
2.2. Experimental dynamic reaction (R_D)

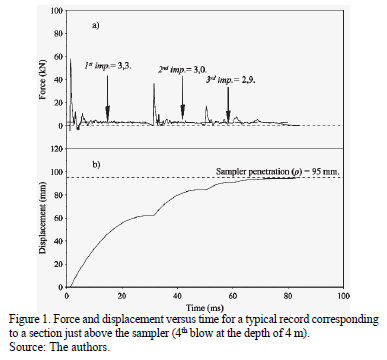
The experimental dynamic reaction for one blow (R_di) is the average of the resultant forces caused by the impacts during the time interval when the SPT sampler is penetrated into the soil (Fig. 1).

The experimental dynamic resistance (R_D) at a certain depth is defined as the average of the values of the experimental dynamic resistance for each blow, divided by the number of blows (N) for the last 0.3 m of the sampler's penetration into the soil (eq. 8).

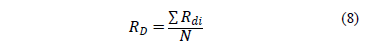
2.3. Reaction forces and stresses developed during the sampler penetration.

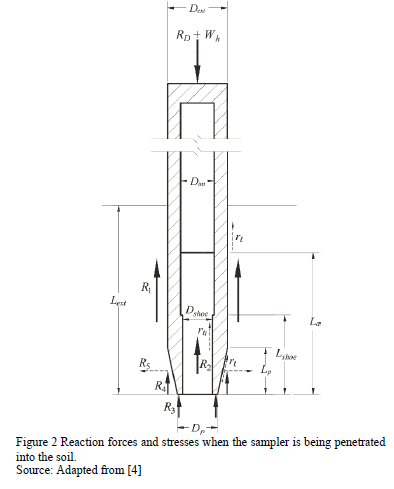
At the instant that the stress wave reaches the sampler, the soil reacts, producing an experimental dynamic force (R_D), which is constituted by the stresses and forces shown in Fig. 2. [4]

The balance of non-conservative vertical forces acting on the sampler (Fig. 2) is represented by:

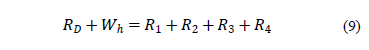
Where:

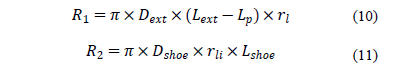
Where,

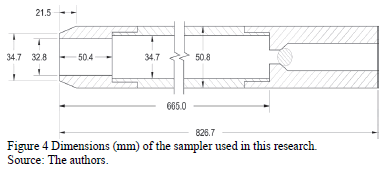
D_ext = 50.8 mm
D_int = 34.7 mm
D_shoe = 32.0 mm
D_p = 34.7 mm
L_p = 21.5 mm
L_shoe = 50.36 mm
D_ext = sampler's external diameter.
D_int = sampler's internal diameter.
D_shoe = sampler's shoe internal diameter.
D_p = sampler's tip diameter.
L_p = sampler's tampered section length.
L_ext = sampler's total penetration.
L_a = sample's length.
L_shoe = sampler's shoe length.
r_l = friction on the sampler's outer surface and chamfer.
r_li = friction on the sampler's inner surface.
R_D = dynamic experimental reaction.
W_h = weight of the rods and anvil.
R₁ = frictional force at the sampler's outer surface.
R₂ = frictional force at the sampler's inner surface.
R₃ = vertical reaction force on the annular section of the sampler's tip (may be considered negligible).
R₄ = vertical component of frictional force along the sampler's tampered surface.
R₅ = horizontal component of frictional force along the sampler's tampered surface.

The balance of non-conservative vertical forces acting on the sampler (Fig. 2) is represented by:

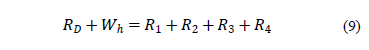
Where

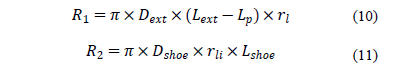
Following Aoki [3], the a parameter can be defined as the ratio of the internal and external friction:

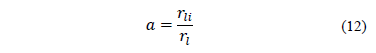
Eq. (11) can be rewritten:

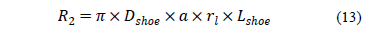
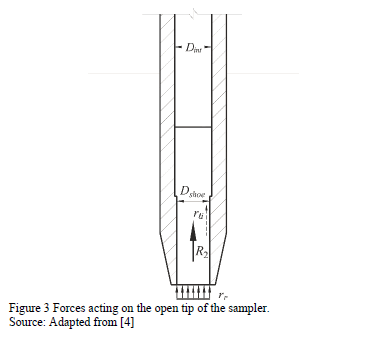
Fig. 3 shows the forces acting on the sampler's open tip of. It can be seen from this figure that R₂ is equal to the resistance reaction acting in the open tip of the standard sampler (eq.14):

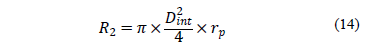
Similarly to the CPT test, the friction ratio (R_f) is defined as the ratio of the external lateral friction and the tip resistance of the soil (r_p).

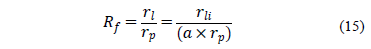
Combining eq. (11), (14) and (15), the following equation is obtained:

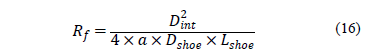
The R₃ and R₄ forces can be assessed by eq. (17) and (18).

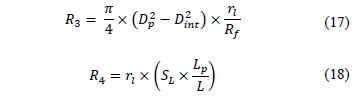
Where,

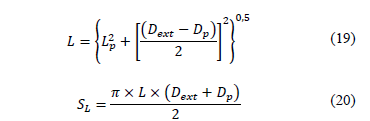
Therefore,

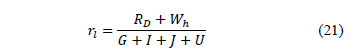
Where,

 

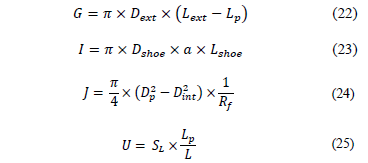
3. SPT equipment

The following is a list of the specifications of the SPT equipment that was used in this research:

• Tripod
• String of rods (24.3-mm inner diameter, 33.4-mm outer diameter. lengths of 1 to 2 m and unit weight of with 32.3-N/m)
• 65-kg pinweight hammer with a wood cushion.
• Anvil (90-mm height, 87.5-mm diameter and 3.3-kg weight)
• Rope (to lift the hammer)
• Conventional couplings (to connect the rods)
• Helical auger
• Raymond type split sampler

4. Instrumentation

4.1. Instrumentation for measuring forces and accelerations

The instrumented subassembly, which was developed by Lukiantchuki [9], consists of one segment of rod in which one load cell and two accelerometers are mounted. For more information about the instrumentation, data logger and software used in this research refer to Zapata [10].

4.2. Equipment for measuring the friction force between the soil and the sampler

An equipment to extract samples from inside the sampler and to evaluate the friction between the soil and the sampler was developed by Zapata [10]. The friction between the soil and the sampler can be evaluated by measuring the force R₂ needed to move the sample inside the sampler. The force R₂ is applied by a hydraulic cylinder and measured by a load cell. This procedure is performed for each meter of the SPT test.

This equipment consists of the following (Fig. 5):

• Naval aluminum base and supports for the sampler and the hydraulic cylinder
• Hydraulic cylinder to apply the sample extracting load
• Load cell (HBM model RSCBC3 with a maximum capacity of 500 kg) to measure the force applied to move the sample inside the sampler (Fig. 6)

The load cell force signals (R₂) are sent to and recorded by a portable data acquisition system (HBM model MX-410), which is controlled by the CatmanEasy software.

From the measured internal shear force R₂ and the experimental dynamic reaction (R_D) corresponding to a specific depth, the remaining reactions (tip, internal and external friction) that take place when the sampler is penetrated into the soil can be assessed. Furthermore, the Aoki's a parameter and the friction ratio (R_f,) are evaluated by using the equations described in section 2.3.

 

5. Results and discussions

5.1. Energy and efficiency

The amounts of energy and the efficiency values at the top of the sampler were determined for the blows that corresponded to the last 0.3 m of the total sampler penetration into the soil.

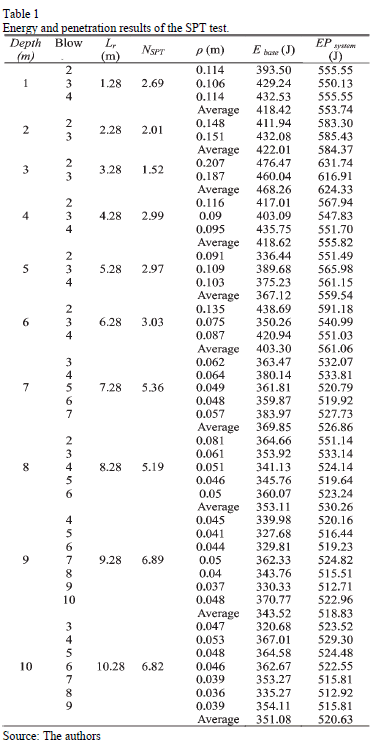
Table 1 shows the penetration of the sampler, the energy estimated at the bottom of the string of rods (top of the sampler, (E_base) and the system's potential energy (EP_system). The differences between the nominal potential energy (EP_i) values and the system's potential energy (EP_system) values (Table 1), show the importance of correcting the energy according to Odebrecht [6].

The system's potential energy that corresponds to higher resistance soil layers (N_SPT > 5 blows) is at least 8.5% higher than the nominal potential energy (478.2 J), whereas in the lower resistance soil layers (N_SPT < 3 blows); this percentage may be as high as 30.6%.

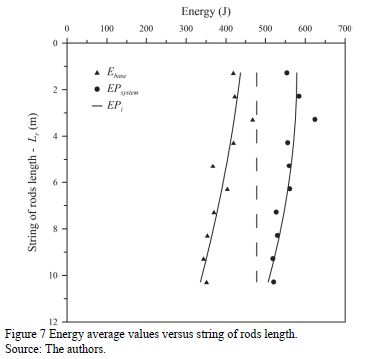
The estimated energy at the base of the string of rods and the system's potential energy curves show a parallel trend (Fig. 7). The distance between the two curves is the energy loss, which can be represented by efficiency (h).

According to Fig. 7, the shorter the length of the string of rods, the greater the system's potential energy and the greater the energy that reaches the sampler.

Table 2 shows the average values of efficiency for the tests conducted in this research as well as the standard deviation and the variation coefficient.

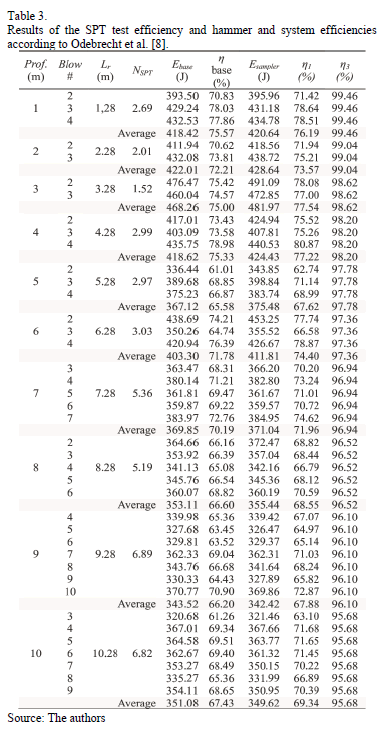
Table 3 displays the SPT test efficiency (h) values, the energy values that reach the sampler (according to Odebrecht et al. [8]), the hammer's efficiencies (h₁), the string of rods' efficiencies (h₂) and the system's efficiencies (h₃). These parameters can be calculated by eq. (4), (5) and (6), respectively.

Table 3 shows the estimated energy at the base of the string of rods (E_base) is lower than the energy that reaches the sampler (E_sampler), calculated by eq. (3) for shorter string of rods. However, if the string of rods' length is increased, the values of E_base will be closer and closer to the sampler's energy values (E_sampler), possibly even exceeding them.

This is the case as the hammer efficiency (h₁) is always higher than the efficiency (h). For longer strings of rods, the influence of the system efficiency (h₃) is higher as it drops from almost 100% to 96%; as a consequence, the energy that reaches the sampler is decreased (E_sampler).

5.2. Reactions and stresses developed during sampler penetration.

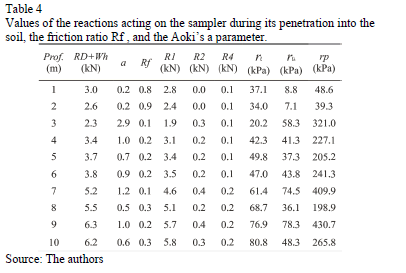
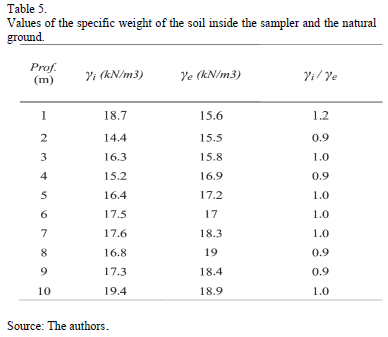
The values of the force R₂ and other reactions acting on the sampler, in addition to Aoki's a parameter [4] and friction ratio (R_f), are shown in Table 4.

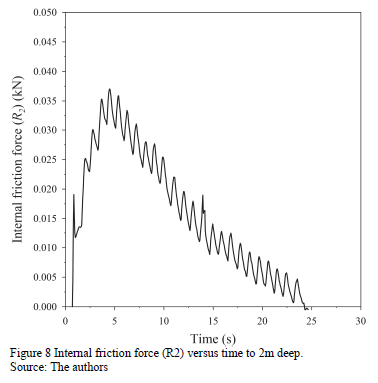
Fig. 8 shows a representative curve of the internal friction force versus elapsed time.

Table 4 shows that Aoki's a parameter values are approximately equal to one for any bore depth, with the exception of 1 and 2 m bore depths. This makes sense as the specific weight of the soil inside the sampler (g_i) and the specific weight of the natural soil (g_e), found in [11] are approximately equal (Table 5).

 

6. Conclusions

The differences between the nominal potential energy (EP_i) values and the system's potential energy (EP_system) values, shown in Table 1, clearly show the importance of correcting the energy according to Odebrecht [6].

The system's potential energy corresponding to soil layers of higher resistance (N_SPT > 5 blows) is at least 8.5% higher than the nominal potential energy (478.2 J), whereas in the lower resistance soil layers (N_SPT < 3 blows) this percentage increases up to 30.6%.

The estimated energy at the base of the string of rods and the system's potential energy curves show a parallel trend. The distance between the two curves is the energy loss, which may be represented by efficiency (h).

The average efficiency at the base of the string of rods is 70.59%, with a standard deviation of 2.46% and coefficient of variation of 3.51.

The estimated energy at the base of the string of rods (E_base) is lower than the energy that reaches the sampler (E_sampler) for shorter string of rods. However, if the string of rods' length is increased, the values of E_base will be closer and closer to the energy values of the sampler (E_sampler), possibly even exceeding them. This is the case as the hammer efficiency (h₁) is always higher than the efficiency (h). For longer strings of rods, the influence of the system efficiency (h₃) is higher as it drops from almost 100% to 96%; as a consequence, the energy that reaches the sampler is decreased (E_sampler).

The development of equipment for estimating the internal friction force (R₂) allowed the stresses acting on the SPT sampler to be evaluated.

The Aoki's a parameter values are approximately equal to one for any bore depth, with 1 and 2 m bore depths being the exception. These results show the efficacy of the new equipment that is designed to estimate the internal friction force (R₂).

 

Acknowledgements

The authors are very thankful to FAPESP (Grant No. 2008/08268-4) and CNPq (Grant No. 479001/2009-0) for their financial support. Furthermore, the first author is very thankful to CNPq for granting her a scholarship that made her Master's thesis possible.

 

References

[1] Diaz-Segura, E.G., Método simplificado para la estimación de la carga última de pilotes sometidos a carga vertical axial en arenas, DYNA, [Online]. 80(179), pp. 109-115, 2013. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/30280/40655.         [ Links ]

[2] ABNT. Associação Brasileira de Normas Técnicas. Solo. Sondagens de simples reconhecimento com SPT. Método de ensaio. In: ABNT (NBR 6484). Associação Brasileira de Normas Técnicas. Rio de Janeiro, Brasil. 2001 pp. 3-12.         [ Links ]

[3] Aoki, N. and Cintra, J.C.A., The application of energy conservation Hamilton's principle to the determination of energy efficiency in SPT tests. Proceedings of International Conference on the Application of Stress Wave Theory to Piles, 6., São Paulo, 1, pp.457-460, 2000.         [ Links ]

[4] Aoki, N., Inovação no SPT, In: Cintra, J.C.A., Aoki, N., Tsuha, C. and Giacheti, H.L., Eds. Fundações, Ensaios estáticos e dinâmicos. São Paulo: Oficina de Textos, 2013. pp. 25-38.         [ Links ]

[5] Schnaid, F., Odebrecht, E., Rocha, M.M. ans Bernardes, G.P., Prediction of soil properties from the concepts of energy transfer in dynamic penetration tests. Journal of Geotechnical and Geoenvironmental Engineering - ASCE, 135(8), pp. 1092-1100, 2009. DOI: 10.1061/(ASCE)GT.1943-5606.0000059        [ Links ]

[6] Odebrecht, E., Medidas de energia no ensaio SPT, PhD Thesis, Departamento de Engenharia Civil, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2003.         [ Links ]

[7] Odebrecht, E., Schnaid, F., Rocha, M.M. and Bernardes, G.P., Energy measurements for standard penetration tests and the effects of the length of rods. Geotechnical and Geophysical Site Characterization, pp. 351-358, 2004. ISBN 90 5966 009 9.         [ Links ]

[8] Odebrecht, E., Schnaid, F., Rocha, M.M. and Bernardes, G.P., Energy efficiency for standard penetration tests. Journal of Geotechnical and Geoenvironmental engineering, ASCE, pp. 1252-1263, 2005.         [ Links ]

[9] Lukiantchuki, J.A., Interpretação de resultados do ensaio SPT com base em instrumentação dinâmica. PhD. Thesis, Department of Geotechnics Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, SP, Brasil, 2012.         [ Links ]

[10] Zapata, J.G., Estimativa das tensões internas e externas atuantes no amostrador SPT durante sua cravação. MSc. Thesis, Department of Geotechnical Engineering, Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, SP, Brasil, 2015.         [ Links ]

[11] Peixoto, A.S.P., Estudo do ensaio SPT-T e sua aplicação na prática de engenharia de fundações. PhD. Thesis, Faculdade de Engenharia Agrícola, Universidade Estadual de Campinas (UNICAMP/FEAGRI). Campinas- SP, Brasil. 2001.         [ Links ]

 

J. Zapata-Galvis, received her BSc. Eng. in Civil Engineering in 2011 from the Escuela de Ingeniería de Antioquia, and her MSc. in Geotechnical Engineering in 2015 from the University of Sao Paulo, Sao Carlos, Brazil. From 2011 to 2013 she worked in the field of geotechnical design in the area of foundations, slopes and retaining walls, soil profile analysis and testing with geotechnical instrumentation (SPT, inclinometers, pressuremeters and CPT). ORCID: 0000-0001-9932-3325.

E.R. Esquivel, received his BSc. Eng. in Civil Engineering in 1971 and his MSc. in Structural Engineering, both from the University of São Paulo, Sao Paulo, Brazil. He earned his PhD. in Geotechnical Engineering from the University of Colorado, Boulder, USA. From 1972 to 1988, he worked for consulting companies that specialized in subway projects. From 1989 to 1995 he worked as research assistant at the University of Colorado USA. Since 2003 he has been a professor at the School of Engineering in Sao Carlos at the University of Sao Paulo, Sao Carlos, Brazil. His research interests include: sub-surface investigation, geotechnical instrumentation, soil-structure interaction, numerical and physical modeling of geotechnical structures, foundation engineering, geotechnical properties of natural and compacted soils and soil improvement. ORCID: 0000-0002-2542-7081