Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.196 Medellín mar./abr. 2016
https://doi.org/10.15446/dyna.v83n196.52492
DOI: http://dx.doi.org/10.15446/dyna.v83n196.52492
Collaborative goods distribution using the IRP model
Distribución colaborativa de mercancías utilizando el modelo IRP
Martín Darío Arango-Serna a, Carlos Andrés-Romano b & Julián Andrés Zapata-Cortés c
a Escuela Ingeniería de la Organización, Universidad Nacional de Colombia - Sede Medellín, Colombia. mdarango@unal.edu.co
b Departamento de Organización de Empresas, Universitat Politècnica de València, España. candres@omp.upv.es
c Investigador Grupo GICO, Universidad Nacional de Colombia - Sede Medellín, Colombia. jazapat1@unal.edu.co
Received: August 14th, 2015. Received in revised form: November 01rd, 2015. Accepted: February 10th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This paper presents a study of the impact that collaboration in inventory has on distribution costs in a network of one supplier and multiple customers. Freight transport is widely studied due to its impact on logistics costs and service levels of enterprises. Looking for network configurations that improve some of these aspects will always be attractive to both academics and businesses. The collaborative distribution system was proposed using the IRP model, and it was compared with the scenarios in which the both supplier or customers optimize their inventory levels. For the IRP model solution a genetic algorithm was used, from which it was obtained a collaborative distribution system with a better performance than if the optimization is made independently.
Keywords: Goods distribution; collaboration; inventory management; IRP; genetic algorithm.
Resumen
Este artículo presenta un estudio sobre el impacto que tiene la distribución colaborativa sobre los costos en la toma de las decisiones del inventario entre un proveedor y múltiples clientes, utilizando el modelo IRP para definir el sistema de distribución. El transporte de mercancías es una actividad ampliamente estudiada debido al impacto tiene en los costos logísticos y en el nivel de servicio de las empresas. Buscar redes de distribución que mejoren alguno de estos aspectos siempre será atractivo tanto para académicos como para las empresas. El resultado producido por el modelo IRP fue comparado con los escenarios en que el proveedor y los clientes optimizan sus niveles de inventario. Para la solución del modelo IRP se utilizó un algoritmo genético, a partir del cual se logro obtener un sistema de distribución en colaboración con un mejor desempeño que el correspondiente cuando la optimización se hace de forma independiente.
Palabras clave: Distribución de mercancías; colaboración; manejo de inventario; IRP; algoritmos genéticos.
1. Introducción
La distribución de mercancías consiste en transportar los productos desde uno o múltiples puntos de origen a uno o múltiples puntos de destino, en donde se pueden encontrar varias instancias como zonas de almacenamiento, crossdocking, pasos interurbanos, pasos urbanos, transito internacional, múltiples escalones, entre muchas otras posibilidades que son especificas de la configuración de las empresas participantes y de la relación entre ellas [1]. Estas actividades son especificas a la configuración de la red y condicionan los costos y el cumplimiento de los niveles de servicio del proceso de distribución [2].
Los procesos de distribución de mercancías requieren sistemas de administración que permitan encontrar mejores condiciones de operación para reducir los costos y asegurar el nivel de servicio, de forma que se logren alcanzar las metas estratégicas de la compañía junto con el desempeño financiero propuesto (rentabilidad esperada) [3]. Uno de los elementos críticos en estos sistemas de distribución, es la inclusión de la variable del inventario [4-7].
El presente articulo presenta un esquema en el cual se resuelve de manera conjunta el problema de la asignación del inventario y la determinación de las rutas para un conjunto de clientes atendidos por un mismo proveedor, en el cual, mediante la decisión centralizada por parte del proveedor, se decide la cantidad de mercancía, el momento de enviarlas y la secuencia de las rutas para este proceso de distribución. Para encontrar la configuración de este proceso de distribución se utiliza el modelo de ruteo de inventario IRP (Inventory Routing Problem), el cual fundamenta su enfoque es la estrategia de colaboración VMI [8-10].
El articulo esta conformado por 4 partes: En la primera se presenta la importancia de incluir la variable inventario en los procesos de distribución y como este proceso puede ser optimizado utilizando el modelo IRP. La segunda parte presenta el enfoque metodológico utilizado para ejemplificar el uso del modelo IRP mediante un algoritmo genético, el cual presenta una nueva forma de representar el individuo. La tercera parte presenta los resultados de la aplicación del modelo y el análisis de resultados, para posteriormente presentar las conclusiones en la cuarta parte.
2. Marco Teórico
Entre las decisiones mas importantes de los procesos de diseño de redes de distribución se encuentra la de asignar adecuadamente el inventario a las instalaciones de la red, lo cual incluye la planificación y determinación de las instancias y el movimiento de los productos en la cadena de distribución [5,7]. Cho et al [11] y Bertazzi y Esperanza [12] mencionan la importancia de incluir dentro de los procesos de distribución de mercancía la variable del nivel de inventario. Estos autores señalan que generalmente los modelos matemáticos implementados para optimizar los costos de transporte se basan en las distancias recorridas y/o en la ubicación de las instalaciones, por lo cual estudiaron la inclusión de los costos de inventario en proveedores y en los clientes, como un elemento fundamental dentro de los procesos de optimización de las redes de transporte.
Para lograr incluir la variable del inventario en los procesos de distribución de mercancías, se hace necesario un proceso de colaboración entre proveedores y clientes, mediante el cual puedan conocerse los pronósticos de demanda y los niveles del inventario y a partir de esto diseñar un esquema de asignación del inventario eficiente para los clientes y para los proveedores [13,14].
La colaboración en la cadena de suministros y particularmente en el manejo del inventario es una estrategia que permite disminuir los costos y mejorar el nivel de servicio en las operaciones de abastecimiento de las empresas y de las propias cadenas [15]. Múltiples autores han estudiado los procesos colaborativos para la toma de decisiones sobre el manejo de inventarios entre empresas [16-21], donde el inventario manejado por el vendedor VMI es la estrategia más comúnmente utilizada a nivel empresarial y mas estudiada a nivel académico [22,23]. El VMI (Vendor Managed Inventory) es el proceso en el cual el vendedor asume la tarea de decidir sobre la asignación del inventario en la cadena de suministros, generando pedidos de compra para el reabastecimiento del inventario de los clientes, mediante un proceso centralizado con el propósito de reducir los costos de almacenamiento y los faltantes de productos en los puntos de distribución [14].
Para resolver el problema de la asignación simultánea de las rutas de transporte y las decisiones del inventario, el modelo mas estudiado es el Problema de Ruteo de Inventario (Inventory Routing Problem - IRP) [22], el cual se basa en la estrategia de inventarios colaborativos manejados por el vendedor (VMI) y que tiene como finalidad combinar el problema de asignación del inventario para reducir los costos de mantener mercancía, al tiempo que optimiza la utilización de los recursos de transporte [9,8,24,25]. El modelo IRP se encarga de asignar el inventario a cada uno de los clientes y a partir de esto asigna las rutas para abastecerlos [10,25,26]. Esto es posible, toda vez que el modelo IRP se basa en el enfoque VMI, en donde las demandas y los niveles del inventarios son conocidos por el proveedor, y es este el responsable de la distribución de las mercancías.
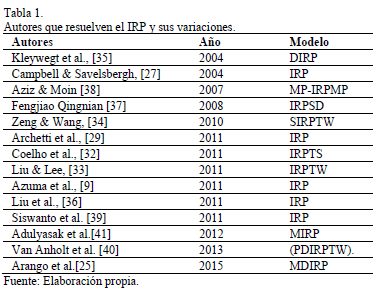
Campbell and Savelsbergh [27] estudiaron el modelo IRP para enfoques de decisión de largo plazo, mediante un esquema de descomposición de las decisiones en dos fases: en la primera se asigna el inventario y en la segunda se generan las rutas. Archetti et al.[8] y Solyali y Süral [28] han propuesto métodos exactos para resolver el modelo IRP para un único vehículo, encontrando dificultades para resolver problemas de grandes dimensiones. Para resolver este inconveniente, Archetti et al., [29] y Azuma [30] han utilizado heurísticas y metaheurísticas respectivamente. El problema de múltiples vehículos ha sido resuelto por Coelho et al., [31] y Coelho et al., [32] utilizando metaheurísticas. La Tabla 1 presenta una revisión de algunos otros trabajos encontrados en la literatura especializada, en los que se encuentra solución para diferentes variaciones del modelo IRP.
En su versión mas simple, el modelo IRP para múltiples vehículos puede ser formulado considerando un grafico Hamiltoniano G = (V,A) donde V es el conjunto de nodos 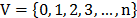 y A es el conjunto de arcos
y A es el conjunto de arcos 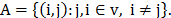 El vértice 0 representa el deposito y
El vértice 0 representa el deposito y 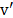 es el subconjunto de vértices en el cual no se incluye el origen.
es el subconjunto de vértices en el cual no se incluye el origen. 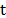 es el periodo, con
es el periodo, con 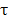 el conjunto de periodos (
el conjunto de periodos (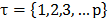 ) y p es el Horizonte de tiempo de la planificación. En el modelo existe un numero limitado de vehículos k
) y p es el Horizonte de tiempo de la planificación. En el modelo existe un numero limitado de vehículos k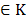 (
(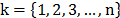 , con capacidad heterogénea. Sea
, con capacidad heterogénea. Sea 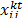 es una variable binaria con valor de 1 si el arco i-j es usado en la ruta del vehículo k en el tiempo t, o cero en otro caso,
es una variable binaria con valor de 1 si el arco i-j es usado en la ruta del vehículo k en el tiempo t, o cero en otro caso, 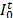 y
y 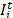 el inventario en el proveedor y los clientes respectivamente y
el inventario en el proveedor y los clientes respectivamente y 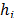 ,
, 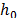 , y
, y 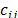 los costos de inventario y transporte.
los costos de inventario y transporte.
A partir de la formulación presentada por Arango et al. [25], el modelo aquí presentado para la distribución entre un proveedor y múltiples clientes, la función objetivo y el conjunto de restricciones para la minimización de los costos de transporte e inventario se escriben como:
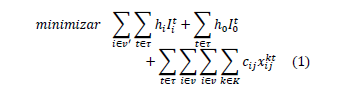
Sujeta a las siguientes restricciones:
1. Restricción de inventario en el proveedor.
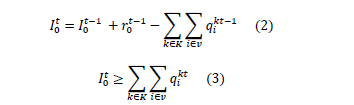
2. Restricción de inventario en los clientes.
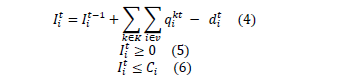
3. Restricciones de política de abastecimiento.
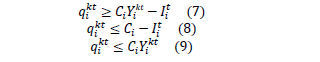
4. Restricciones de capacidad del vehículo.
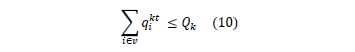
5. Restricciones de ruteo.
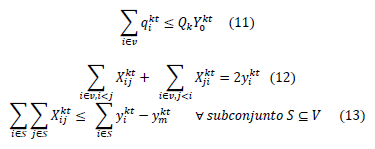
6. Restricciones de no-negatividad.
Todas las variables presentadas en el modelo, son mayores o iguales a cero, por lo cual 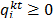 ;
; 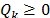 ;
; 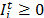 ;
; 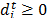 ;
; 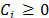 .
.
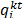 es la cantidad enviada al cliente i,
es la cantidad enviada al cliente i, 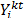 es una variable binaria que toma el valor 1 si el nodo i es visitado por el vehículo k en el periodo t, o cero de otra forma. La función objetivo de la eq. (1) busca la minimización del inventario y de los costos de Transporte. Las ecuaciones de política de abastecimiento eq. (7)-(9) aseguran que cuando un cliente es visitado, la cantidad de mercancía que debe recibir sea lo que le falte para llegar a su inventario máximo (
es una variable binaria que toma el valor 1 si el nodo i es visitado por el vehículo k en el periodo t, o cero de otra forma. La función objetivo de la eq. (1) busca la minimización del inventario y de los costos de Transporte. Las ecuaciones de política de abastecimiento eq. (7)-(9) aseguran que cuando un cliente es visitado, la cantidad de mercancía que debe recibir sea lo que le falte para llegar a su inventario máximo (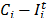 ), Las restricciones de ruteo aseguran que se genere una ruta adecuada en el periodo t, de forma que se visiten todos los clientes que deben ser servidos en dicho periodo. En este sentido, la eq. (11) asegura que si al menos un cliente es visitado, luego la ruta debe visitar al proveedor. La eq. (12) representa que si el nodo (cliente) i es visitado, debe haber un arco para la entrada y un arco para la salida de dicho nodo. La suma de estos arcos debe ser igual a 2
), Las restricciones de ruteo aseguran que se genere una ruta adecuada en el periodo t, de forma que se visiten todos los clientes que deben ser servidos en dicho periodo. En este sentido, la eq. (11) asegura que si al menos un cliente es visitado, luego la ruta debe visitar al proveedor. La eq. (12) representa que si el nodo (cliente) i es visitado, debe haber un arco para la entrada y un arco para la salida de dicho nodo. La suma de estos arcos debe ser igual a 2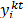 , con lo cual se asegura que si y solo si existen dichos arcos. La restricción de la eq. (13) evita la generación de sub-rutas del vehículo k en el tiempo t. Esto quiere decir que para cada subconjunto S, la cantidad de arcos debe ser menor o igual que el numero de nodos menos 1, con lo cual se asegura que solo se cree el tour de la solución.
, con lo cual se asegura que si y solo si existen dichos arcos. La restricción de la eq. (13) evita la generación de sub-rutas del vehículo k en el tiempo t. Esto quiere decir que para cada subconjunto S, la cantidad de arcos debe ser menor o igual que el numero de nodos menos 1, con lo cual se asegura que solo se cree el tour de la solución.
Otras restricciones pueden ser formuladas para incluir extensiones del problema como ventanas de tiempo, múltiples depósitos, múltiples productos, entregas y recogidas simultaneas, etc. [10,40,42,43]. En la literatura científica especializada es posible encontrar trabajos de investigación que incluyen el inventario en los procesos de distribución de mercancías, que aunque no son enfoques colaborativos, al ser definidos para una única empresa, permiten abordar los procesos de integración de estas variables desde un enfoque mas complejo. Estos trabajos, dentro de los que se encuentran los desarrollados por Chang y Yen [44], Pradhananga et al. [45] y Melián-Batista et al. [46] generalmente utilizan procesos de optimización multiobjetivo para la propuesta de sistemas de transporte que incluyen las decisiones de inventario de forma conjunta con el diseño de las rutas para la distribución de mercancías.
3. Materiales y Métodos
En este artículo se busca evaluar el desempeño del modelo IRP para resolver un problema de distribución de mercancías. Para esto se analiza un problema definido en la literatura científica, a partir del cual se calculan los costos de la distribución optimizando el inventario en las instalaciones de los clientes y en el proveedor, y obteniendo el costo del ruteo con el uso del modelo VRP. Estos resultados son comparados con los costos obtenidos mediante la solución con el modelo IRP. La configuración de la red de distribución corresponde a la instancia de un proveedor, 15 clientes y un horizonte de tiempo de tres periodos, definida por Archetti et al. [8].
Para encontrar la solución tanto al modelo VRP como al IRP, se desarrollaron dos algoritmos genéticos, uno para VRP y otro para IRP. Debido a que el objetivo del modelo aquí presentado (un proveedor con múltiples clientes) es evaluar el IRP, solamente el algoritmo genético desarrollado para su solución será descrito. Ambos algoritmos genéticos fueron programados en Java, utilizando el entorno de desarrollo integrado NetBeans IDE.
3.1. Algoritmo genético para la solución del modelo IRP
Los algoritmos genéticos han demostrado ser herramientas adecuadas para resolver problemas matemáticos complejos [47,48], como es el caso de los problemas de ruteo de vehículos [49-51]. Para resolver el problema IRP, en la literatura científica el numero de trabajos que utilizan algoritmos genéticos o evolutivos es limitado, encontrándose los desarrollados por Azuma [30], Azuma et at. [9], Liu et al. [36], Fengjiao y Qingnian [37], Aziz y Moin [38], Aydin [52] y Cho et al. [11].
La principal diferencia entre estos trabajos se encuentra en la forma de representar el individuo (cromosoma) para su solución. Algunos autores para su solución presentan dos matrices, en las cuales se asigna la cantidad a enviar a cada cliente y la secuencia de las rutas, respectivamente. Otros autores utilizan una matriz en la cual de manera conjunta se representa la asignación del inventario y de las rutas de cada vehículo.
3.1.1. Representación del individuo
En este artículo se adopta la representación conjunta, con la diferencia que directamente el individuo indica la cantidad de mercancía a enviar a cada cliente, así como la secuencia de visita de los clientes que debe seguir cada vehículo. En la Tabla 2 se presenta un ejemplo de la forma del cromosoma utilizado en el algoritmo propuesto, el cual es una matriz en la cual las filas corresponden a los periodos del horizonte de planificación, y en las columnas se genera la asignación del inventario para cada uno de los clientes y luego la secuencia de la ruta a seguir.
En la Tabla 2 se observan las dos partes del cromosoma utilizado para un individuo con cinco clientes y tres periodos de planificación. La parte en gris corresponde a las cantidades asignadas a cada cliente (c) en el respectivo periodo (p). La parte sin sombrear corresponde a las rutas para la distribución de dichas cantidades. El algoritmo determina la mejor ruta con base en las cantidades a distribuir en cada periodo. De esta forma, en el periodo 1 solo se utiliza un vehículo, el cual debe partir del almacén del proveedor (punto cero) visitar los clientes en el respectivo orden 5-1-3 y volver al almacén. Por su parte, para el periodo 2 se requieren dos vehículos debido a que la carga sobrepasa la capacidad de los mismos, con lo cual el vehículo 1 debe visitar los clientes 1 y 4, y el vehículo 2 los clientes 5 y 2 en ese respectivo orden. Cada vez que se realiza una operación de cruce o mutación el algoritmo analiza el individuo y corrige las rutas, con lo cual siempre cada vehículo estará separado por un cero en el cromosoma.
3.1.2. Evaluación del individuo y selección
La evaluación del individuo (Función aptitud) se realiza calculando los costos totales de almacenamiento y transporte para el horizonte de planificación, con base en la eq. (1), que corresponde a la función objetivo del problema IRP. En este caso los mejores individuos son aquellos que presenten los menores valores de la función de aptitud. Los individuos son obtenidos por torneo aleatorio, cuyo tamaño equivale al 20% de la población.
3.1.3. Inicialización de la población
Cada individuo (cromosoma) de la población inicial del algoritmo genético se genera aleatoriamente. En este caso, las cantidades a enviar a cada cliente corresponden a un numero aleatorio entre la demanda del periodo y la cantidad máxima permitida si el cliente requiere ser abastecido, o cero en el otro caso. Las rutas son asignadas aleatoriamente y posteriormente corregidas dependiendo si se envía o no mercancía a todos los clientes.
3.1.4. Operador de cruce
El cruce de los cromosomas padres para producir nuevos individuos se realiza con un operador de cruzamiento similar al propuesto por Cho et al.[11], para el cruce vertical en el inventario y cruce de dos puntos para las rutas de un mismo periodo. En este procedimiento de cruce, los nuevos individuos se obtienen intercambiando las cantidades de todos los periodos de un mismo cliente de los padres para la parte del inventario. En la parte de las rutas, mediante cruce de dos puntos para cada periodo se realiza la recombinación para obtener el nuevo individuo. Una vez obtenidos los nuevos individuos, el algoritmo ajusta el cromosoma para obtener secuencia de ruteo factibles.
3.1.5. Operador de mutación
La mutación de individuos se realiza como es habitual de forma aleatoria. En este caso para la parte del inventario se utiliza un operador similar al propuesto por Cho et al.[11], en la cual la cantidad a enviar a un cliente escogido aleatoriamente se modifica, y el restante de la cantidad se compensa en el mismo cliente en los periodos previos o posteriores. Para la parte de las rutas, la mutación se realiza utilizando el método de intercambio simple (Swap) para un punto en cada uno de los periodos, también aleatoriamente. De forma similar a lo realizado con el operador de cruce, una vez la mutación termina, el cromosoma es ajustado para obtener secuencias de ruteo factibles.
4. Resultados
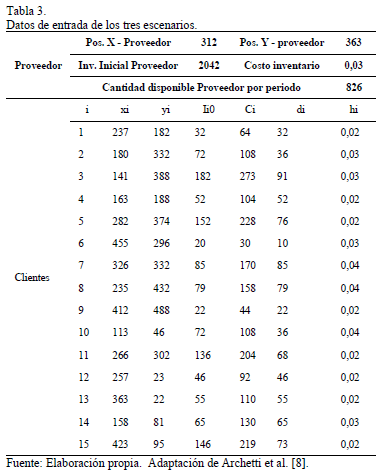
La información de la instancia tomada de Archetti et al. [8] que es utilizada para este articulo se presenta en la Tabla 3, a partir de la cual se obtiene la información requerida para realizar la simulación de los tres escenarios evaluados: Optimización del inventario en las instalaciones de los clientes, optimización del inventario en la instalación del proveedor y colaboración.
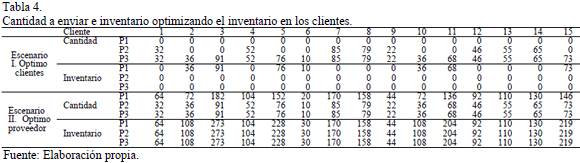
El optimo del inventario en las instalaciones de los clientes se obtiene logrando que el inventario en el horizonte de clientes sea el mínimo sin que existan faltantes, mientras que el optimo en el proveedor se logra enviando la mayor cantidad posible a los clientes, hasta que estos alcancen su nivel máximo. De esta forma, la cantidad a enviar a cada uno de los clientes y el inventario en cada periodo para los 2 escenarios mencionados se presenta en la Tabla 4. La Tabla 5 presenta el inventario para el proveedor.
A partir de la asignación del inventario en cada uno de estos dos primeros escenarios se calculan las rutas utilizando el modelo VRP. La Tabla 6 presenta las rutas encontradas utilizando un algoritmo genético para su solución. En esta tabla se observa que con las condiciones de distribución solo se requiere un vehículo para realizar el ruteo de las mercancías. Para todos los casos en que se requiera servir la totalidad de los clientes se asigna la mejor ruta obtenida por el algoritmo.
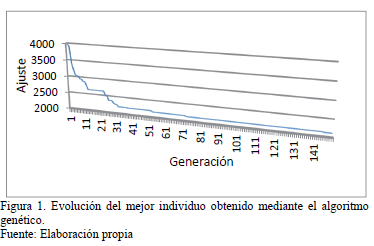
El tercer escenario, correspondiente a la colaboración entre el proveedor y los clientes se calcula utilizando algoritmo genético propuesto para resolver el modelo IRP. El algoritmo genético utilizado para resolver el problema colaborativo fue probado utilizando 200 individuos y a partir de 150 generaciones no se encontraron resultados que mejoraran la calidad de la solución, tal y como se observa en la Fig. 1.
El mejor individuo encontrado por el algoritmo después de las 150 generaciones presentadas en la Fig. 1 y que corresponden a la mejor solución para el problema de distribución colaborativo, se presenta en la Tabla 7, de la cual se puede observar la asignación del inventario y las rutas para cada uno de los periodos del horizonte de planificación.
A partir del mejor individuo se obtiene las cantidades a enviar y el inventario en cada clientes, como se observa en la Tabla 8. El inventario en el proveedor y las rutas generadas por el algoritmo para el esquema en colaboración se presentan en las Tablas 9 y 10 respectivamente.
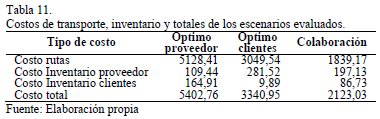
Los costos obtenidos en cada uno de los escenarios estudiados son presentados en la Tabla 11, a partir de la cual se puede observar que los costos de la colaboración son inferiores a los obtenidos en cualquiera de los otros escenarios. Cuando se busca optimizar de forma independiente el inventario por alguna de las partes es posible obtener un costo mínimo en cada una de ellas (El inventario es mínimo en los clientes para el escenario I y mínimo en el proveedor en el escenario II), sin embargo ese optimo local genera que las actividades de transporte se intensifiquen para abastecer los clientes con las condiciones definidas para cada escenario, ocasionando que los costos de transporte se incrementen considerablemente y por tanto alejándose del optimo global del sistema. En el esquema colaborativo el inventario en los clientes o en los proveedores no se acerca a los valores óptimos encontrados en los escenarios I o II, sin embargo, debido a la centralización de las decisiones del inventario, los costos de distribución se reducen notablemente, ya que los clientes son visitados el menor numero de veces posible sin generar faltantes de producto, obteniendo en vez del optimo local del inventario, el optimo global del sistema de distribución.
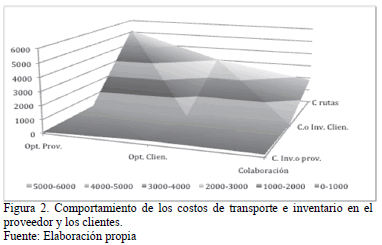
La Fig. 2 presenta el grafico de superficie para el análisis de los costos estudiados, a partir de la cual se observa que los costos que generan mayor impacto son los correspondientes al transporte, ya que los de inventario son muy inferiores en magnitud, y son los que mas influyen para obtener el optimo global del sistema. Esto permite argumentar que las empresas por no realizar acciones colaborativas pueden realizar esfuerzos en actividades que generan poco valor.
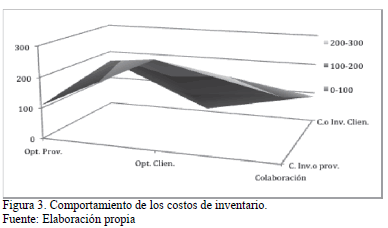
Analizando el comportamiento solo para el inventario en las instalaciones de los proveedores y clientes, tal y como se muestra en la Fig. 3, se observa que al llevar el inventario al menor para alguna parte ocasiona que en la contraparte se obtenga el peor valor del inventario, lo cual influye en el aumento de costos en el sistema. Para el caso en que se realiza la colaboración, como se mencionó anteriormente, no se obtiene el valor mínimo para el proveedor o para los compradores, sino un valor intermedio que no significa deteriorar llevar este valor a condiciones desfavorables para la contraparte, lo cual posibilita que el sistema de distribución sea mas eficiente, tal y como se demostró utilizando el modelo IRP.
Como medida del desempeño del algoritmo genético en este problema en particular, se realiza la comparación de la solución obtenida con otros resultados publicados en la literatura científica. En este mismo problema Azuma [30] reporto una solución con un costo total de 2131.04 y Coelho [53] reporto un costo total de 2236,53. A partir de estos resultados se puede argumentar que el algoritmo presentado arroja buenas soluciones para resolver la instancia utilizada para el ejemplo presentado. Sin embargo antes de poder argumentar que el algoritmo se comporta mejor que los presentados por los autores mencionados, deben realizarse las pruebas con las demás instancias y variaciones propuestas por Archetti et al.[8] o por Archetti et al. [54].
5. Conclusiones
Este artículo presenta una propuesta para optimizar la planificación conjunta de las operaciones de inventario y distribución entre un proveedor y múltiples clientes forma colaborativa. El proceso de distribución colaborativa basado en el IRP y en modelo VMI, permite disminuir significativamente los costos del proceso, comparado con cuando solamente y de forma independiente se busca optimizar los niveles de inventario en las instalaciones de los clientes o en las instalaciones de los proveedores.
En la distribución colaborativa las cantidades del inventario no se acercan a los valores óptimos del proveedor o de los clientes, pero al poder determinar de manera conjunta las cantidades a transportar y los momentos para hacerlo, se obtiene una reducción importante en el transporte, lo que hace que los costos totales del sistema sean inferiores comparados con los óptimos independientes.
EL modelo IRP es una alternativa adecuada para la formulación de problemas en los que los diseñadores de la red de distribución cuentan con la posibilidad de coordinar de manera conjunta los inventarios de los clientes y proveedores, toda vez que este modelo se basa en el modelo de inventarios colaborativos VMI y soporta la decisión de ruteo los enfoques del agente viajero (TSP) cuando se tiene un único vehículo y en el ruteo de vehículos (VRP) para los otros cosos.
Para la solución del modelo IRP presentado se utilizó un algoritmo genético, el cual presenta una representación novedosa de los individuos para este tipo de problemas (Cromosoma). Según el conocimiento de los autores, esta es la primera vez que esta representación es presentada en la literatura especializada para resolver el modelo IRP. Los resultados obtenidos con el algoritmo genético para la instancia analizada, la cual corresponde a una configuración comúnmente estudiada en la literatura científica, demuestra que el algoritmo presenta buenos resultados en la solución del modelo IRP.
Agradecimientos
Los autores agradecen a la Universidad Nacional de Colombia por el apoyo al proyecto "Optimización de la distribución de mercancías utilizando un modelo genético multiobjetivo de n proveedores con m clientes", código Hermes: 29314. Proyecto del cual se deriva este artículo de investigación.
Referencias
[1] Rushton, A., Croucher, P. and Baker, P., The handbook of logistics and distribution management, 3rd edition, Ed. Kogan Page Limited. 2010. ISBN 0-7494-4669-2 [ Links ]
[2] Estrada, M.A., Análisis de estrategias eficientes en la logística de distribución de paquetería. Tesis Doctoral. Programa de Doctorado de Ingeniería Civil E.T.S. de Ingenieros de Caminos, Canales y Puertos de Barcelona. Universitat Politècnica de Catalunya, España. 2007. [ Links ]
[3] Adarme, W., Arango, MD. and Balcazar, D.A., Modelo para la coordinación de agentes en un sistema logístico de la industria Astillera Colombiana. Revista Ingeniería e Investigación. 31(2), pp.102-111, 2011 [ Links ]
[4] Hernández, S., Peeta, S. and Kalafatas, G., A less-than-truckload carrier collaboration planning problem under dynamic capacities. Transportation Research Part E 47, pp. 933-946, 2011. [ Links ]
[5] Moin, N.H; Salhi, S. and Aziz, N.A.B., An efficient hybrid genetic algorithm for the multi-product multi-period inventory routing problem. Int. J. Production Economics, 133 pp. 334-343, 2011. [ Links ]
[6] Deflorio, F., Gonzalez-Feliu, J., Perboli, G. and Tadei, R., The influence of time windows on the costs of urban freight distribution services in city logistics applications. EJTIR, 12(3), pp. 256-274, 2012. [ Links ]
[7] Antún, J.P., Distribución urbana de mercancías: Estrategias con centros logísticos. Banco Interamericano de Desarrollo. Departamento de Infraestructura y Medio Ambiente. Nota técnica # IDB-TN-167. [Online]. 2013. Available at: http://publications.iadb.org/facet-view?field=type_view. [ Links ]
[8] Archetti, C., Bertazzi, L., Laporte, G. and Speranza, M.G., A branch-and-cut algorithm for a vendor-managed inventory-routing problem. Transportation Science, 1(3), pp 382-391, 2007. [ Links ]
[9] Azuma, R., Coelho, G.P. and Von Zuben, F.J., Evolutionary multi-objective optimization for the vendor-managed inventory routing problem. In EEE Congress on Evolutionary Computation (CEC), pp. 1457-1464. 2011. [ Links ]
[10] Coelho, L.C. and Laporte, G., The exact solution of several classes of inventory-routing problems. Computers & Operations Research 40, pp.558-565, 2013. [ Links ]
[11] Cho, D.W., Hae-Lee, Y., Youn-Lee, T. and Gen, M., An adaptive genetic algorithm for the time dependent inventory routing problema. Journal Intelligent Manufacturing, 25, pp. 1025-1042, 2014. [ Links ]
[12] Bertazzi, L. and Esperanza, M.G., Inventory routing problems with multiple customers. EURO J Transp Logist, 2, pp. 255-275, 2013. [ Links ]
[13] Zhang, D., Liu, X. and Li, S., An optimization model for multi-period collaborative inventory control based on target performance management. Proceedings of the 2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design, pp. 930-934, 2012 [ Links ]
[14] Arango, M.D., Zapata, J.A. and Adarme, W., Aplicación del modelo de inventario manejado por el vendedor en una empresa del sector alimentario colombiano. Revista EIA, 15, pp. 21-32, 2011. [ Links ]
[15] Arango, M.D., Adarme, W. and Zapata, J.A., Inventarios colaborativos en la optimización de la cadena de suministros. DYNA, 80(181), pp. 71-80, 2013. ISSN 0012-7353 [ Links ]
[16] Zavanella, L. and Zanoni, S., A one-vendormulti-buyer integrated production-inventory model: The 'ConsignmentStock'case. Intern. Journal of production Economics, 118, pp. 225-232, 2009. [ Links ]
[17] Kwak, C., Choi, J.S., Kim, C.O. and Kwonc, I.-H., Situation reactive approach to Vendor Managed Inventory problema. Expert Systems with Applications, 36(5), pp. 9039-9045, 2009. [ Links ]
[18] Fawcett, S., Waller, M. and Fawcett, A., Elaborating a dynamic systems theory to understand collaborative inventory successes and failures. The International Journal of Logistics Management, 21(3), pp. 510-537, 2010. [ Links ]
[19] Arango-Serna, M.D., Serna-Urán, C.A. and Alvarez-Uribe, K.C., Collaborative autonomous systems in models of urban logistics. DYNA, 79(172). 2012. [ Links ]
[20] Díaz-Batista, J. and Pérez-Armador, D., Optimización de los niveles de inventario en una cadena de suministro, Ingeniería Industrial, 33(2), pp. 126-132, 2012. [ Links ]
[21] Zhang, T., Liang, L., Yu, Y. and Yu, Y., An integrated vendor-managed inventory model for a two-echelon system with order cost reduction. International Journal of Production Economics, 109(1-2), pp. 241-253, 2007. [ Links ]
[22] Abdelmaguid, T.F. and Dessouky, M.M., A genetic algorithm approach to the integrated inventory-distribution problema. International Journal of Production Research, 44(21), pp. 4445-4464, 2006. [ Links ]
[23] Gonzalez-Feliu, J., Peris-Pla, C. and Rakotonarivo, D., Simulation and optimization methods for logistics pooling in the outbound supply chain. Third International Conference on Value Chain Sustainability. Towards a Sustainable Development and Corporate Social Re- sponsibility Strategies in the 21st Century Global Market, Nov 2010, Spain. pp. 394-401, 2010. [ Links ]
[24] Archetti, C., Bianchessi, N., Irnich, S. and Speranza, M.G., Formulations for an inventory routing problem. Intl. Trans. in Op. Res. 21, pp. 353-374, 2014. [ Links ]
[25] Arango, M.D., Zapata, J.A. and, Gutierrez, D., Modeling the inventory routing problem (IRP) with multiple depots with genetic algorithms. IEEE Latin American Transactions. 13(12), pp. 3959-3965, 2015. [ Links ]
[26] Zeng, Z. and Zhao, J., Study of stochastic demand inventory routing problem with soft time windows based on MDP. Adv. in Neural Network Research & Appli., LNEE(67), pp. 193-200, 2010. [ Links ]
[27] Campbell A.M. and Savelsbergh, M.W.P., A decomposition approach for the inventory-routing problem. INFORMS Transportation Science 38(4), pp. 488-502, 2004 [ Links ]
[28] Solyali, O and Süral H., A branch-and-cut algorithm using a strong formulation and an a priori tour based heuristic for an inventory-routing problem. Transportation Science; 45(3), pp. 335-345, 2011. [ Links ]
[29] Archetti, C, Bertazzi, L, Hertz, A. and Speranza, M.G., A hybrid heuristic for an inventory routing problem. INFORMS Journal on Computing, pp. 101-116, 2011. [ Links ]
[30] Azuma, R.M., Otimização multiobjetivo em problema de estoque e roteamento gerenciados pelo fornecedor. Tesis MSc., Departamento de Engenharia de Computação e Automação Industrial, Universidade Estadual De Campinas, Brasil, 2011. [ Links ]
[31] Coelho L.C, Cordeau, J-F. and Laporte, G., Consistency in multi-vehicle inventory- routing. Transportation Research Part C; 24(1), pp. 270-287, 2012. [ Links ]
[32] Coelho, L.C, Cordeau, J.F. and Laporte G., The inventory-routing problem with transshipment. Cirrelt. [Online]. 2011. https://www.cirrelt.ca [ Links ]
[33] Liu, S.C. and Lee, W.T., A heuristic method for the inventory routing problem with time windows. A heuristic method for the inventory routing problem with time Windows, pp. 13223-13231, 2011. [ Links ]
[34] Zeng, Z. and Wang, J., Study of stochastic demand inventory routing problem with soft time windows based on MDP. Adv. in Neural Network Research & Appli., LNEE(67), pp. 193-200, 2010. [ Links ]
[35] Kleywegt, A.J., Nori, V.S. and Savelsbergh, M.W.P., Dynamic programming approximations for a stochastic inventory routing problem. Transportation Science 38(1), pp 42-70, 2004. [ Links ]
[36] Liu, G-S., Lin, K-P., Lee, H-W. and Wang, C-Y., A study of inventory-routing problem for the distribution system by applying genetic algorithm. IEEE International Summer Conference of Asia Pacific, pp. 104-108, 2011. [ Links ]
[37] Fengjiao, W. and Qingnian, Z., The research on the inventory routing problem with split pick-ups based on genetic algorithm. WiCOM '08. 4th International Conference on Wireless Communications, Networking and Mobile Computing, pp. 1-4, 2008. [ Links ]
[38] Aziz, N.A.B. and Moin, N.H., Genetic algorithm based approach for the multi product multi period inventory routing problem. IEEE International Conference on Industrial Engineering and Engineering Management, pp. 1619-1623, 2007 [ Links ]
[39] Siswanto, N., Essam, D., and Sarker, R., Multi-heuristics based genetic algorithm for solving maritime inventory routing problem. IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), pp. 116-120, 2011. [ Links ]
[40] van Anholt, R., Coelho, L., Laporte, G. and Vis, I., An inventory-routing problem with pickups and deliveries arising in the replenishment of automated teller machines. CIRRELT. [Online]. 2013. Available at: https://www.cirrelt.ca [ Links ]
[41] Adulyasak, Y., Cordeau, J-F. and Jans, R., Formulations and branch-and-cut algorithms for multi-vehicle production and inventory routing problems. Technical report G-2012-14, GERAD, Montreal, Canada; 2012. [ Links ]
[42] Lien R.W., Iravani S.M.R., Smilowitz, K. and Tzur, M., An efficient and robust design for transshipment networks. Production and Operations Management; 20(5), pp. 699-713, 2011. [ Links ]
[43] Coelho, L.C. and Laporte, G., A branch and cut algorithm for the multi product multi vehicle inventory routing problem. CIRRELT-2012-53. [Online]. 2012. Available at: https://www.cirrelt.ca [ Links ]
[44] Chang, T-S. and Yen, H-M., City-courier routing and scheduling problems. European Journal of Operational Research, 223, pp. 489-498, 2012. [ Links ]
[45] Pradhananga, R., Taniguchi, E., Yamada, T. and Qureshi. A.G., Bi-objective decisión support system for routing and scheduling of hazardous materials. Socio-Economic Planning Sciences, 48, pp. 135-148, 2014. [ Links ]
[46] Melián-Batista, B., De Santiago, A., Bello, F.A. and Alvarez, A., A bi-objective vehicle routing problem with time windows: A real case in Tenerife. Applied Soft Computing, 17, pp. 140-152, 2014. [ Links ]
[47] Vidal, T., Crainic, T.G., Gendreau, M. and Prins, C., Heuristics for multi-attribute vehicle routing problems: A survey and synthesis. Montreal: Cirrelt. 2012. [ Links ]
[48] López, A, Zapotecas S. and Coelho, L.C., An introduction to multiobjective optimization techniques. In Ajith A., Lakhmi J. and Goldberg R. (Eds.), Evolutionary multiobjective optimization: Theoretical advances and applications, pp. 7-32, Springer-Verlag, London, ISBN 1-85233-787-7. 2009. [ Links ]
[49] González, G. y González, F., Metaheurísticas aplicadas al ruteo de vehículos. Un caso de estudio. Parte 2: Algoritmo genético, comparación con una solución heurística. Revista Ingeniería e Investigación. 27(1), pp. 149-157, 2007. [ Links ]
[50] Arango, M.D. and Serna, C.A., A memetic algorithm for the traveling salesman problem. IEEE Latin America Transactions,13(8), 2015. DOI: 10.1109/TLA.2015.7332148. [ Links ]
[51] Arango, M.D., Zapata, J.A. and Andres, C., Metaheuristics for goods distribution. Proceedings of 2015 International Conference on Industrial Engineering and Systems Management (IESM), IEEE Publications, pp.99-107, 2015. DOI. 10.1109/IESM.2015.7380143 [ Links ]
[52] Aydín, N., A genetic algorithm on inventory routing problem. Emerging Markets Journal. 3(3), pp. 59-66, 2014. [ Links ]
[53] Coelho, L.C., Inventory-Routing. [Online]. [Date of reference: August 11th of 2015]. Available at: http://www.leandro-coelho.com/instances/inventory-routing/ [ Links ]
[54] Archetti, C., Bertazzi, L., Hertz, A. and Speranza, M.G., A hybrid heuristic for an inventory routing problem. INFORMS Journal on Computing, 24(1), pp. 101-116, 2012. [ Links ]
M.D. Arango-Serna, graduado como Ing. Industrial en 1991 en la Universidad Autónoma Latinoamericana,, Colombia, Esp. en Finanzas, Formulación y Evaluación de Proyectos en 1993 por la Universidad de Antioquia, Colombia, Esp. en Docencia Universitaria en 2007 por la Universidad Politécnica de Valencia, España, MaSc. en Ingeniería de Sistemas en 1997 por la Universidad Nacional de Colombia - Sede Medellín, Dr. Ingeniero Industrial en 2001 por la Universidad Politécnica de Valencia, España. Es profesor titular en dedicación exclusiva, adscrito al Departamento de Ingeniería de la Organización, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín. Es Investigador Senior según clasificación Colciencias 2015. Director del Grupo de I+D+i Logística Industrial- Organizacional "GICO", grupo A1. Los temas de trabajo en los cuales se desempeña el profesor Arango-Serna están relacionados con procesos logísticos en la cadena de suministros, Investigación de operaciones, diseños de plantas, técnicas de optimización industrial-Organizacionales, entre otras. ORCID: 0000-0001-8448-8231
C. Andrés-Romano, graduado como Ing. Industrial en 1995 y como Dr. en Ingeniería Industrial en 2001, en la Universidad Politécnica de Valencia, España. Actualmente se desempeña como profesor titular, en el Departamento de Organización de Empresas de la Universidad Politécnica de Valencia, España. Las temáticas en las que se desenvuelve el profesor Andrés-Romano son en el estudio de tiempos y métodos para el mejoramiento de procesos, programación y administración de proyectos, desarrollo de metaheurísticas para resolver problemas de optimización industrial, entre otros. ORCID: 0000-0003-4453-4891
J.A. Zapata-Cortes, graduado como Ing. Químico en 2006, como MSc. en Ingeniería Administrativa en 2011 y candidato a Dr. en Ingeniería - Industria y Organizaciones en la Universidad Nacional de Colombia. Actualmente se desempeña como investigador en el grupo de I+D+I Logística Industrial-Organizacional "GICO" de la Universidad Nacional de Colombia. Investigador Junior según clasificación Colciencias 2015. Los temas en los que se desenvuelve son en la optimización de redes de transporte e inventario, tecnologías de la información y la comunicación aplicadas a la cadena de suministro y a la administración de procesos empresariales, entre otros. ORCID: 0000-0002-1270-3577