Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.196 Medellín mar./abr. 2016
https://doi.org/10.15446/dyna.v83n196.53222
DOI: http://dx.doi.org/10.15446/dyna.v83n196.53222
Baseflow analysis using master recession curves and numerical algorithms in mountain basins: Suratá's river and Oro's river (Santander, Colombia)
Análisis de flujo base usando curvas maestras de recesión y algoritmos numéricos en cuencas de montaña: Cuenca del río Suratá y cuenca del Río de Oro (Santander, Colombia)
Sully Gómez-Isidro a & Viviana Lucía Gómez-Ríos b
a Escuela de Ingeniería Civil, Universidad Industrial de Santander, Bucaramanga, Colombia. sgomez@uis.edu.co
b Ingeniera Civil, Universidad Industrial de Santander, Bucaramanga, Colombia. vilugori92@gmail.com
Received: September 26th, 2015. Received in revised form: February 23th, 2016. Accepted: March 17th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The interaction between groundwater inflow and outflow is complex in streams connected from aquifers located in fractured rock media. The recession curves of hydrographs provide information about these hydrogeological processes and they are useful to assess an insight in the storage-discharge relationship in subsurface reservoirs. In this study, the physic base and the nonlinearity relationship of storage-discharge were analyzed through a mathematical expression which describe a master recession curve. Four numerical algorithms were applied to estimate the baseflow of the Suratá's River basin and the high Oro's River basin, Santander-Colombia. In both cases, master recession curves showed the nonlinearity relationship in storage-discharge. Furthermore, the exponent values and the proportionality constants give additional information about the aquifers in contact to the river and the special scale of recharges that may occur in these aquifers.
Keywords: master recession curve; baseflow separation; numerical filters; nonlinearity.
Resumen
Las interacciones entre flujo de entrada y flujo de salida del agua subterránea en ríos conectados con acuíferos localizados en ambientes de rocas fracturadas son complejas. Las curvas de las recesiones en los hidrogramas ofrecen información sobre estos procesos hidrogeológicos y permiten observar la relación almacenamiento-descarga de los reservorios subterráneos. En este trabajo se estudió la base física y la validez de la forma lineal de la relación almacenamiento-descarga que describe la curva maestra de recesión. Se aplicaron cuatro algoritmos numéricos que estimaron el porcentaje de flujo base en las cuencas del río Suratá y Río de Oro, Santander, Colombia. Las curvas maestras de recesión mostraron que la relación almacenamiento-descarga no es lineal y que los valores del exponente y la constante de proporcionalidad ofrecen información sobre el tipo de acuíferos en contacto con los ríos y la escala espacial en la que puede ocurrir la recarga a estos acuíferos.
Palabras clave: curva maestra de recesión; separación de flujo base; filtros numéricos; no linealidad.
1. Introducción
Los almacenamientos hídricos subterráneos proveen de agua a las corrientes de los ríos en temporadas de precipitaciones bajas o nulas, cuando los niveles freáticos son más altos que los niveles del río y por tanto el río es ganador. Estos almacenamientos en contacto con ríos pueden abastecer comunidades con agua de buena calidad, debido a que por su naturaleza se encuentran libres de turbiedad y patógenos, lo que la hace, en general, apta para el consumo humano.
La fracción de flujo base respecto al flujo total en el río es un valor que puede ser utilizado como indicador de sostenibilidad de la reserva hídrica en cuencas [1]. Es por esto que la literatura científica ha dedicado gran esfuerzo al conocimiento del flujo base de los ríos [2-4].
Los métodos para la separación de flujo base se clasifican principalmente en métodos gráficos, químicos (isótopos estables del agua) y algoritmos numéricos (filtros) con base física, estos últimos utilizan series de tiempo de caudales. En estudios de separación de flujo base conviene aplicar varios métodos para poder contrastar los resultados. Entre algunos de los algoritmos numéricos disponibles se encuentran programas de computador de libre acceso como, HYSEP [5], PULSE [6], RECESS [7], WHAT [8] y el método de BFI [9], considerados como algoritmos que tienen poca base física. Ellos fueron creados para tener procesos repetibles, fácilmente programables y se han utilizado para tener una primera aproximación al valor del flujo base [10]. En la actualidad las técnicas de filtros han incorporado elementos que incluyen una base física, la mayoría de ellos reflejan la recesión del hidrograma [11], otros hacen algunas simplificaciones considerando un balance de masas en laderas [12] o consideran que la infiltración tiene una componente rápida y otra lenta, como el Modelo IACRES [13].
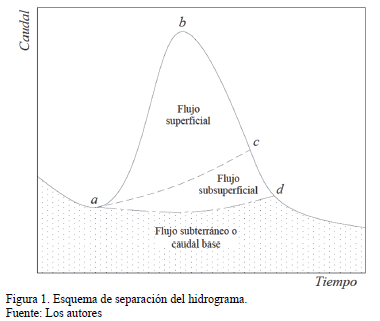
En la Fig. 1 se observa un esquema de separación. El flujo base o flujo subterráneo está representado por la parte baja del hidrograma y la línea formada por el punto a y el punto d durante el evento de lluvia, mientras que el flujo subsuperficial es delimitado por la curva anterior y otra entre los puntos a y c. En este trabajo se enfatiza en la separación del hidrograma en dos componentes: el flujo subterráneo y el flujo superficial. Las curvas de recesión representan la disminución de los almacenamientos subterráneos en contacto con las corrientes, pueden ofrecer información sobre las características físicas e hidrodinámicas de las formaciones geológicas, porosidad, conductividad hidráulica y capacidad especifica. Ellas son utilizadas para estimar recarga a acuíferos, caudales mínimos o de estiaje en ríos y tiempos de recesión. La curva maestra de recesión (CMR) es una curva generalizada de recesiones del flujo en un río que ofrece una percepción de la capacidad y agotamiento del almacenamiento subterráneo.
La curva maestra de recesión ha sido considerada como una herramienta expedita y de uso generalizado en la hidrología, que expresa una función exponencial decreciente. Por lo regular, el uso de la CMR resulta válido en ríos de valles aluviales donde la contribución principal del flujo base proviene de acuíferos aluviales conectados de forma local con el río; en estos casos, las áreas influenciadas por estos acuíferos son importantes para la protección de la calidad del agua superficial. Sin embargo, en condiciones geológicas complejas y topografías fuertes [14] la contribución del flujo base puede provenir de almacenamientos subterráneos localizados en zonas altas (altiplanos y cordilleras) y el caudal base puede estar relacionado con caudales de largo plazo [15].
En este trabajo se estudian e interpretan las curvas de recesión del hidrograma en dos cuencas de montaña localizadas sobre el macizo de Santander (Colombia) que abastecen de agua a través de bocatomas a una comunidad de cerca de un millón de habitantes de la ciudad de Bucaramanga y su área metropolitana. El flujo subterráneo que alimenta el flujo base en estas cuencas presenta algunas particularidades relacionadas con la geología que pudieron ser observadas en el estudio de las curvas de recesión. Se aplican cuatro algoritmos numéricos desarrollados en el programa G2 [16] para obtener la fracción del flujo base y se obtienen parámetros que expresan el concepto de no linealidad en la recesión de los almacenamientos subterráneos. Estos resultados se contrastan con valores obtenidos mediante otros métodos. El flujo base en estas cuencas es una reserva importante que debe ser tenida en cuenta en los planes de manejo y gestión del recurso hídrico y en otorgamiento de licencias ambientales, los cuales deben considerar flujos de larga distancia que alimentan el caudal base de estos ríos, de lo contario el agua de las bocatomas será afectada en cantidad y en calidad.
2. Metodología
Se presenta una revisión y análisis de la forma matemática de la curva de recesión y una breve descripción tanto de los algoritmos numéricos utilizados para realizar la separación del flujo base, de las condiciones hidrogeológicas de la zona de estudio relacionadas con las recesiones de los hidrogramas y métodos utilizados.
2.1. Revisión de la forma matemática de la curva de recesión de los hidrogramas
El hidrograma es una gráfica que representa la variación temporal del caudal medido en un punto de un río o de una corriente. Los parámetros físicos de la cuenca (geomorfología, cobertura, uso del suelo) y las características geológicas de las formaciones acuíferas en contacto con el río, determinan la forma y las magnitudes relativas de las componentes de los hidrogramas.
El descenso o agotamiento del agua almacenada en el acuífero en épocas de estiaje o pocas lluvias da lugar a la recesión. La CMR es el resultado de la superposición de todas las curvas de recesión que han ocurrido a lo largo de una serie de tiempo de caudales. La pendiente de la recta formada por la CMR en la escala logarítmica es la llamada constante de recesión del río en el punto de interés. La forma matemática de la CMR ha sido interpretada con una función exponencial decreciente como se muestra en la ecuación (1).
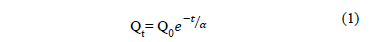
El valor de 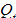 representa el caudal en el tiempo t,
representa el caudal en el tiempo t, 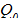 es la caudal inicial y
es la caudal inicial y 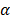 es el índice de recesión que representa el tiempo de vida media o tiempo promedio en el que una gota de agua que ingresa al acuífero en contacto con el río [17]. Otro término físico significativo en la evaluación de una CMR es la constante de recesión k en días-1, que representa la pendiente de la curva de caudales en escala semilogarítmica y también corresponde al inverso del índice de recesión. La función exponencial en la ecuación (1) supone que el acuífero reacciona como un simple reservorio lineal donde el volumen almacenado es proporcional a la salida del flujo del acuífero (S = aQ, a es una constante de proporcionalidad dependiente del área, porosidad del suelo, conductividad hidráulica y propiedades geomorfológicas, [13]. En la gráfica de
es el índice de recesión que representa el tiempo de vida media o tiempo promedio en el que una gota de agua que ingresa al acuífero en contacto con el río [17]. Otro término físico significativo en la evaluación de una CMR es la constante de recesión k en días-1, que representa la pendiente de la curva de caudales en escala semilogarítmica y también corresponde al inverso del índice de recesión. La función exponencial en la ecuación (1) supone que el acuífero reacciona como un simple reservorio lineal donde el volumen almacenado es proporcional a la salida del flujo del acuífero (S = aQ, a es una constante de proporcionalidad dependiente del área, porosidad del suelo, conductividad hidráulica y propiedades geomorfológicas, [13]. En la gráfica de 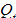 contra t, en escala logarítmica, se observa una línea recta. Este comportamiento puede ser característico de cuencas que, principalmente, presentan acuíferos confinados constituidos por formaciones geológicas homogéneas y gradientes hidráulicos suaves. Sin embargo, se conoce que en cuencas donde existen acuíferos heterogéneos conformados por rocas fracturadas, meteorizadas o carbonatadas, con presencia de laderas muy inclinadas, no es posible representar el sistema con la ecuación que representa reservorios lineales y la curva de recesión no se ajusta a un único valor de k [11].
contra t, en escala logarítmica, se observa una línea recta. Este comportamiento puede ser característico de cuencas que, principalmente, presentan acuíferos confinados constituidos por formaciones geológicas homogéneas y gradientes hidráulicos suaves. Sin embargo, se conoce que en cuencas donde existen acuíferos heterogéneos conformados por rocas fracturadas, meteorizadas o carbonatadas, con presencia de laderas muy inclinadas, no es posible representar el sistema con la ecuación que representa reservorios lineales y la curva de recesión no se ajusta a un único valor de k [11].
El concepto físico de no linealidad en el flujo subterráneo ha sido estudiado por algunos autores que han desarrollado modelos basados en la combinación de depósitos lineales para proporcionar una mejor forma a la curva de recesión [19, 20], mientras que otros han propuesto una relación no lineal entre el almacenamiento y la descarga, adicionando un exponente b a la ecuación de un reservorio lineal [18, 21], como se muestra en la siguiente ecuación:
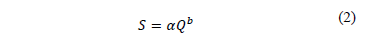
Donde 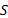 es el volumen de almacenamiento disponible para ser descargado en la corriente y
es el volumen de almacenamiento disponible para ser descargado en la corriente y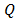 es el caudal de descarga,
es el caudal de descarga, 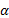 tiene unidades de medida de
tiene unidades de medida de 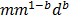 si el almacenamiento es dado en mm y el caudal en
si el almacenamiento es dado en mm y el caudal en 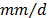 y
y 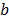 es una variable adimensional. La ecuación (1) es un caso particular en el que la ecuación diferencial es despejada teniendo en cuenta que
es una variable adimensional. La ecuación (1) es un caso particular en el que la ecuación diferencial es despejada teniendo en cuenta que 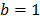 [11], en este caso se trata de un reservorio lineal y se asume que la salida Q del acuífero es linealmente dependiente del almacenamiento S.
[11], en este caso se trata de un reservorio lineal y se asume que la salida Q del acuífero es linealmente dependiente del almacenamiento S.
La ecuación (2) puede ser considerada una ecuación cuadrática cuando b toma el valor de 0.5, y en este caso se trata de una aproximación teórica de la salida de flujo desde acuíferos no confinados cuya solución implica la condición de Dupuit-Forcheimer. El caso particular b=1 caracteriza un acuífero no confinado horizontal [4]. Variaciones de estos valores implican que la realidad del flujo subterráneo hacia ríos no es representada con las consideraciones teóricas anteriores. Resolviendo la ecuación (2) con la ayuda de la ecuación de continuidad en términos de flujo de salida de un reservorio (esto significa que no hay entradas superficiales de acuíferos, ni precipitación, ni flujos profundos, ni salida por evapotranspiración) 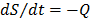 , la solución para el reservorio no lineal cuyo agotamiento empieza con un valor de descarga inicial
, la solución para el reservorio no lineal cuyo agotamiento empieza con un valor de descarga inicial 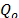 , fue propuesta por [22] y se expresa en la ecuación (3).
, fue propuesta por [22] y se expresa en la ecuación (3).
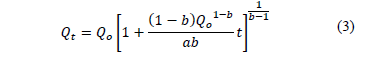
Esta es una ecuación que representa en forma general la curva de recesión del hidrograma. Los parámetros a y b, representan propiedades o condiciones de los acuíferos en contacto con el río.
En los hidrogramas construidos con los datos de caudales se identifican las temporadas de recesión a través de líneas rectas descritas por la ecuación (4). Las curvas de recesión se agrupan para generar la CMR.
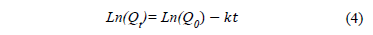
La metodología para obtener la CMR consiste en graficar la serie de datos de caudales junto con los eventos de precipitación registrados en estaciones cercanas a la estación de medición de caudales; esto permite observar la consistencia de las épocas de recesión seleccionadas. En una etapa posterior, se visualizan en una gráfica independiente las recesiones registradas. En este paso se busca tener en una misma Fig., las temporadas de recesión, para ir formando grupos de recesiones alineadas de tal manera que se integren una o varias líneas tangentes a los datos. Por último, se realiza una regresión lineal con todos los datos para identificar el valor de los parámetros de la ecuación (4). Estos valores deben ser analizados en conjunto con las condiciones físicas de la cuenca como son: las características geológicas y topográficas, el tipo de acuífero y las condiciones del suelo.
2.2. Algoritmos numéricos para separación de flujo base
Los algoritmos numéricos basados en las curvas de recesión fueron creados para reproducir, a partir de hidrogramas, señales de alta frecuencia (respuesta de flujo superficial) y señales de baja frecuencia (respuesta del flujo base) en forma repetitiva [14]. El hidrograma está conformado por un flujo rápido que representa el flujo superficial originado por eventos de precipitación, y por un flujo más lento relacionado con el flujo subterráneo. El uso de algoritmos numéricos, es una técnica de separación automática utilizada cuando se cuenta con series de tiempo de caudales, permite que el flujo base se ajuste a la forma del hidrograma en los tramos de recesión.
Los algoritmos también son llamados filtros numéricos, y hacen referencia a procesos simples con resultados muy sensibles a los parámetros del filtro. Los parámetros son constantes que representan, en su mayoría, condiciones físicas de la cuenca o propiedades del hidrograma. Para que los resultados puedan ser considerados válidos los parámetros deben ser obtenidos mediante un proceso de calibración [23]. Durante el proceso de calibración los parámetros se ajustan haciendo que el hidrograma y el flujo base se asemejen a la curva de recesión. Para ello se escogen tramos de recesiones en las cuales se evalúe la forma del flujo base y se calculen los porcentajes de error relativo en los tramos de las épocas de recesión. Una primera aproximación se realiza utilizando periodos del hidrograma de diez a veinte días, buscando el mejor ajuste según metodología mostrada en [24]. El objetivo de aplicar los algoritmos numéricos es hallar la fracción del flujo base respecto al flujo total y analizar los valores de los parámetros de recesión.
En este trabajo la separación del flujo base se realizó mediante el uso de algoritmos programados en el código de Matlab llamado G2 [16]. Esta herramienta requiere, como datos de entrada, series de tiempo de caudales en escalas horarias o diarias. En la Tabla 1 se describen cuatro de los algoritmos desarrollados en el programa G2 así como los parámetros utilizados en cada uno de ellos. Una descripción más detallada de estos algoritmos se presenta en [14].
2.3. Descripción de la zona de estudio
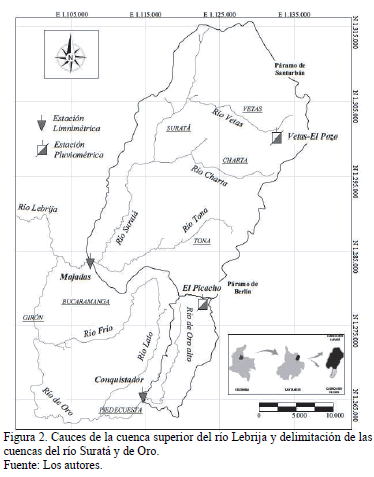
La metodología anterior fue aplicada a los caudales medidos en el río Suratá y en el Río de Oro, localizados sobre la parte montañosa de la cuenca Superior del Río Lebrija (Fig. 2). Estos ríos surten de agua potable a la ciudad de Bucaramanga y al municipio de Piedecuesta, respectivamente, en el departamento Santander. La precipitación en esta zona ocurre a lo largo del año con un óptimo pluviométrico que puede alcanzar 2000 milímetros anuales localizado entre 1800 y 2000 ms.n.m. La precipitación anual presenta una tendencia bimodal acorde con el paso de la Zona de Convergencia Intertropical (ZCIT) que pasa sobre la región generando dos épocas lluviosas en los meses de marzo, abril y mayo, posteriormente en los meses de septiembre, octubre y noviembre, y dos épocas secas o menos lluviosas en los meses de diciembre, enero, febrero, junio y julio [29]. En estas cuencas hasta la fecha no han funcionado proyectos de regulación de caudal y en general son cuencas que no han tenido afectación antrópica drástica, con excepción de las actividades dedicadas a la minería del oro en el páramo de Santurbán.
La cuenca del río Suratá tiene un área de 697 km2 y está conformada por las subcuentas de los ríos Tona, Charta y Vetas; la altura mínima es de 700 ms.n.m y la cota de elevación máxima está localizada en la parte alta de la microcuenca del río Vetas, a 4200 ms.n.m, con una pendiente media del 7.5%; por su parte, la cuenca del Río de Oro tiene un área de 80 km2, el punto más bajo de la cuenca está localizado 1100 ms.n.m y el más alto en 3500 ms.n.m, con una pendiente media del 10%. El río Suratá nace en la parte alta del páramo de Santurbán y el Río de Oro en cercanía al páramo de Berlín.
Las cuencas se localizan sobre un basamento ígneo metamórfico que comprende las unidades gneis de Bucaramanga, formación Silgará, ortogneis, tonalita y granodiorita, cuarzomonzonita de la Corcova y de Santa Bárbara, así como una franja sedimentaria conformada por las formaciones Los Santos y Rosablanca, principalmente. Las rocas cristalinas se encuentran afectadas por intenso fracturamiento y meteorización, lo que ha llevado a la generación de suelos residuales espesos [30] que favorecen el flujo subterráneo y la formación de acuíferos. Además, la cuenca del río Suratá y la del Río de Oro se encuentran delimitadas en un área de complejidad estructural producto del cruce de las fallas Suratá y Cucutilla [31], así como las fallas de los ríos Charta, La Cristalina, Tona y de Oro entre otras, las cuales generan escarpes con fuertes pendientes presentes en ambas cuencas. Por su parte, en la cuenca del río Suratá se identifica un patrón de fracturamiento en dirección NE en escala regional alineado a las fallas Cucutilla y Suratá, relacionado con corredores formados por rocas que tienen porosidad secundaria y constituyen potenciales canales de flujo de aguas subterráneas. Los levantamientos de campo de las direcciones de diaclasas y estrías de falla, así como la localización de manantiales, sugieren una dirección de flujo que pone en conexión la zona alta del páramo de Santurbán y el páramo de Berlín con las zonas bajas del río Charta [32].
Aunque aún no existen datos geológicos concluyentes, los inventarios de manantiales en la cuenca del río Tona [33] permiten inferir que el sistema de flujo del río Charta puede estar comunicado con sistemas de fracturas presentes en la cuenca del río Tona. Por otro lado, en la parte alta de la cuenca del Río de Oro, en límites con el altiplano de Berlín, se encuentran rocas como la cuarzomonzonita de Santa Bárbara (cristalinas) y las rocas de la formación Rosablanca (calizas); esta última se identifica como una formación hidrogeológica tipo cárstica, donde se localizan numerosos manantiales [34]. Las cuarzomonzonitas presentan suelos residuales arenosos producto de la meteorización, que favorecen el flujo subterráneo y la formación de acuíferos.
El modelamiento hidrológico realizado en la cuenca alta del Río de Oro ha mostrado que puede existir un flujo subterráneo resultante de áreas externas a la cuenca [35], por lo tanto, no se descarta la existencia de flujos subterráneos provenientes del altiplano de Berlín.
A partir de estudios de isótopos estables se ha encontrado que la principal recarga de los acuíferos de la meseta de Bucaramanga proviene de la zona montañosa del macizo de Santander, cuyas zonas de recarga pueden extenderse hasta alturas mayores a los 3000 ms.n.m., asociadas a flujos de larga a media distancia [36]. Valores isotópicos tomados en el flujo base del Río de Oro (estación Conquistador) indican que la parte más alta del macizo contribuye en mayor proporción a la recarga de los acuíferos en contacto con los ríos en la zona de montaña [37]. La parte del flujo base del Río de Oro en la estación Conquistador fue estimado mediante la aplicación de isótopos estables en la ecuación de conservación de masa en una sección del río y equivale a cerca del 80 % del flujo total [38].
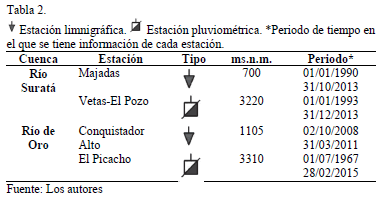
En la cuenca del río Suratá se localiza una estación limnimétrica (Majadas) y una estación pluviométrica (Vetas -El Pozo). Asimismo, en la cuenca del Río de Oro se ubica una estación limnigráfica (Conquistador Alto) y una estación pluviométrica (El Picacho). Las estaciones de caudales se encuentran localizadas para ambos casos aguas arriba de bocatomas, con excepción de las bocatomas que se localizan en la cuenca del río Tona desde hace más de 50 años. La información general de estas estaciones se muestra en la Tabla 2.
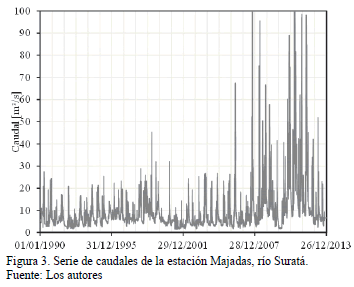
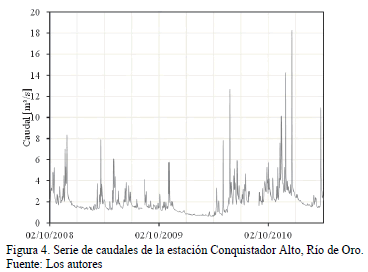
Las gráficas de las series de tiempo de los caudales en los puntos de cierre de las cuencas de rio Suratá y rio de Oro se muestran en la Fig. 3. y Fig 4. Se observan que las variaciones temporales de caudales altos ocurren durante los años 2010 y 2011. Los caudales mínimos se observan regularmente en las épocas secas.
2.4. Selección de algoritmos de separación flujo base
Para seleccionar el algoritmo numérico que ofrece mejores resultados se utiliza el coeficiente de determinación, R2 [39]. Este coeficiente expresa el ajuste entre el caudal del río y el caudal base hallado para cada algoritmo durante las épocas de estiaje; se calcula únicamente con datos de las temporadas de recesión. El análisis se realiza bajo la hipótesis de que todo el flujo en épocas de estiaje proviene de los acuíferos, es decir, el caudal observado 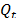 corresponde al flujo base
corresponde al flujo base 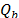 .
.
3. Análisis de resultados
A continuación, se presentan los resultados obtenidos en las dos cuencas de estudio después de aplicar la metodología propuesta y los conceptos presentados en este trabajo.
3.1. Curva maestra de recesión
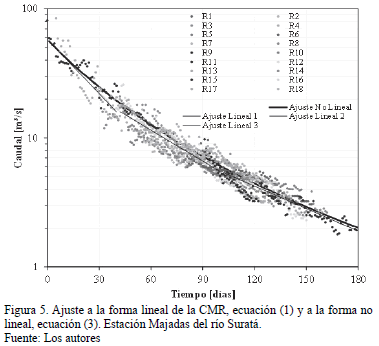
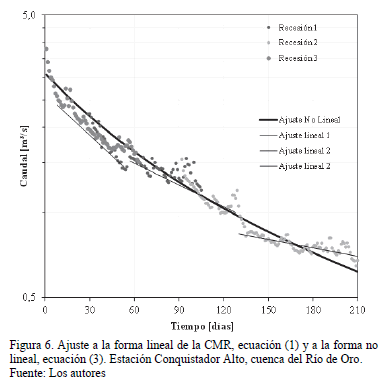
La revisión de la información limnimétrica en la estación Majadas permitió identificar dieciocho periodos de recesión ocurridos entre 1990 y 2013, mientras que para la estación Conquistador Alto se tiene información desde 2008 hasta 2011, y fueron identificadas tres épocas de recesión. En la cuenca del río Suratá se observan recesiones cuya duración varía entre 30 y 101 días, y en el Río de Oro, entre 63 y 120 días. En el Río de Oro, a pesar de tener un periodo de tiempo menos representativo en datos, se encontró la recesión de mayor duración.
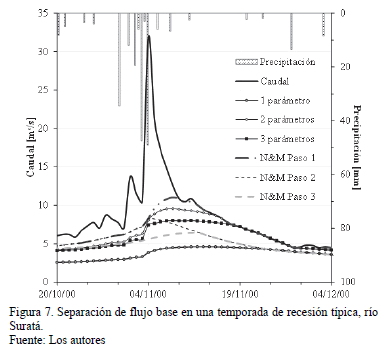
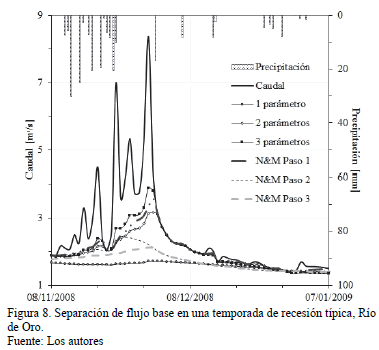
La información pluviométrica en ambas cuencas muestra una relación de la lluvia diaria con la respuesta de los caudales diarios, tal como se observa en la Fig. 7 y en la Fig. 8. Con los datos de las series de caudales de ambos ríos se construyeron las respectivas curvas maestras de recesión.
Se observó que no es posible distinguir una tendencia lineal única en el comportamiento del flujo base de ambos ríos. La CMR obtenida en el río Suratá (Fig. 5) muestra que existen tres comportamientos diferenciables, cada uno con una pendiente característica, por lo tanto, la forma de la ecuación lineal (1) no resulta representativa para este río. Por esta razón se optó por realizar un nuevo ajuste a una ecuación no lineal (3) que represente de mejor forma el comportamiento de todas las recesiones encontradas; el resultado del ajuste igualmente se muestra en la Fig. 5. El coeficiente de determinación (R2) obtenido en este caso fue 0.963.
La CMR del Río de Oro (Fig. 6) también muestra que existen tres comportamientos diferentes, en consecuencia, la forma de la ecuación lineal tampoco es representativa. El ajuste a una forma no lineal presenta un coeficiente de determinación (R2) de 0.956.
En el río Suratá y en el Río de Oro las curvas de recesión presentan forma no lineal y en este caso se ajustaron a una forma cóncava (Ecuación (3)). Un análisis de las tendencias permite observar que la respuesta rápida de la descarga del flujo subterráneo (constante de recesión mayor 0.012 1/día para el río de Oro y 0.032 1/día para el río Suratá) puede corresponder a la movilización de flujo proveniente de recargas más locales, mientras que la respuesta lenta (constant de recesión menor, 0.002 para el río de Oro y 0.013 para río Suratá) corresponde a un retardo del flujo generado en los caminos de mayor distancia que comunican a los acuíferos con el río; en este caso el flujo es alimentado con recargas de larga distancia.
La forma general de la curva maestra de recesión muestra los valores obtenidos de los parámetros a y b, para ambos ríos en la Tabla 3. En el río Suratá y en el Río de Oro el exponente b toma valores de 0.7 y 0.4 respectivamente. Ambos difieren de los exponentes utilizados en los modelos teóricos, que son 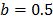 (aproximación cuadrática) o
(aproximación cuadrática) o 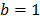 (aproximación lineal). En este caso se deben estudiar las razones para las cuales pueden existir diferencias de estos valores. Valores diferentes significan que en la realidad el flujo no puede ser representado mediante las aproximaciones anteriores. El valor para el Río de Oro es de 0.4, y si bien no es muy diferente a 0.5, puede expresar flujo desde acuíferos libres en contacto con el río. Valores de 0.4 podrían explicarse según [11], en términos de convergencia del flujo subterráneo. Sin embargo, [18] expone otras razones para estos valores, que van desde disminución de conductividad hidráulica con la profundidad, variación espacial de la lluvia y la infiltración, así como el comportamiento transitorio de la relación almacenamiento-descarga, que no son consideradas en las ecuaciones. Esta última razón puede implicar efectos de histéresis o variabilidad del gradiente hidráulico del acuífero. Todas estas condiciones se pueden presentar en la realidad, en particular, en el caso de cuencas de montañas con geologías complejas.
(aproximación lineal). En este caso se deben estudiar las razones para las cuales pueden existir diferencias de estos valores. Valores diferentes significan que en la realidad el flujo no puede ser representado mediante las aproximaciones anteriores. El valor para el Río de Oro es de 0.4, y si bien no es muy diferente a 0.5, puede expresar flujo desde acuíferos libres en contacto con el río. Valores de 0.4 podrían explicarse según [11], en términos de convergencia del flujo subterráneo. Sin embargo, [18] expone otras razones para estos valores, que van desde disminución de conductividad hidráulica con la profundidad, variación espacial de la lluvia y la infiltración, así como el comportamiento transitorio de la relación almacenamiento-descarga, que no son consideradas en las ecuaciones. Esta última razón puede implicar efectos de histéresis o variabilidad del gradiente hidráulico del acuífero. Todas estas condiciones se pueden presentar en la realidad, en particular, en el caso de cuencas de montañas con geologías complejas.
En el río Suratá el exponente b toma un valor de 0.7, que también difiere de los modelos teóricos, pero en este caso se aleja de la aproximación cuadrática y se acerca al valor de 1 más representativo de acuíferos confinados en contacto con el río. El valor obtenido de 0.7 se puede explicar en términos de una componente de un flujo que quizás se origine en la existencia de macroporos o fracturas.
Por otro lado, el valor del parámetro a de las cuencas se ha encontrado mediante el proceso de ajuste (ajuste de la forma de la curva a los datos de la CMR). Este parámetro se relaciona con parámetros físicos de los acuíferos como la porosidad y la conductividad hidráulica, o con características generales de las cuencas.
En las cuencas del río Suratá y del Río de Oro se obtuvieron valores, para a, de 150 y 380 respectivamente, como se observa en la Tabla 3. Los promedios de los parámetros corresponden al enfoque lineal
Los valores obtenidos de a se comparan con valores obtenidos en cuencas de Alemania y China [40], donde se utilizaron resultados de más de veinte cuencas, observándose una relación entre el valor de a y el área de la cuenca. En este trabajo se advierte que el río Suratá muestra un valor semejante a los encontrados en las cuencas anteriores que tienen áreas semejantes. Sin embargo, el valor de a obtenido para el Río de Oro difiere considerablemente de los resultados anteriores. De acuerdo con la relación encontrada, el valor de a correspondería a cuencas con áreas mayores a 1400 km2. El valor de a obtenido para la cuenca del Río de Oro también confirma tiempos de viaje bastantes mayores que los que presenta la cuenca del río Suratá.
3.2. Separación de flujo base
La separación del flujo base se realizó aplicando cuatro algoritmos numéricos (capítulo 2.2) a las series de datos de caudales de los ríos Suratá y de Oro.
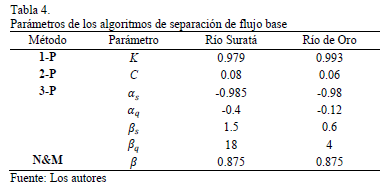
El algoritmo numérico de un parámetro requiere de un solo valor de constante de recesión; al existir tres valores diferentes se optó por el procedimiento clásico de utilizar el valor promedio de las constantes de recesión como representativo del valor K (ver Tabla 3).
El algoritmo de dos parámetros, además del parámetro K anterior, utiliza el parámetro C, que proporciona mayor flexibilidad a la ecuación del algoritmo. El proceso de calibración permitió observar que el porcentaje de flujo base se incrementa a medida que aumenta el valor de C, lo cual indica que, debido a la permeabilidad de la cuenca, en eventos de lluvia la recarga local ocurre más rápidamente y satura el suelo convirtiendo el exceso de agua en escorrentía directa [16]. Asimismo, el proceso de calibración llevó a escoger 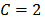 como el mejor valor. Por su parte, la inspección visual del hidrograma y de la línea de separación permitió observar que este algoritmo sobrestima el caudal base en eventos de precipitación y lo subestima en los periodos de estiaje.
como el mejor valor. Por su parte, la inspección visual del hidrograma y de la línea de separación permitió observar que este algoritmo sobrestima el caudal base en eventos de precipitación y lo subestima en los periodos de estiaje.
En el algoritmo de tres parámetros la disposición de la ecuación (7) permite ver que el factor 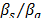 expresa el flujo rápido y el flujo lento, cuya relación puede tener una interpretación similar a la constante C del algoritmo de dos parámetros.
expresa el flujo rápido y el flujo lento, cuya relación puede tener una interpretación similar a la constante C del algoritmo de dos parámetros.
El algoritmo desarrollado por Nathan & McMahon se desarrolla en tres pasos, cada paso obtiene un valor menor de flujo base como porcentaje del flujo total, debido a que cada uno de estos se basa en los resultados del anterior. Para finalizar, se observó que el paso 1 es el que mejor se acopla a la forma del hidrograma en la recesión.
En la Tabla 4 se observan los valores de los parámetros obtenidos durante la calibración de los diferentes algoritmos numéricos utilizados.
Después de aplicar la técnica de algoritmos numéricos a los datos de caudales se obtuvo el porcentaje de flujo base con respecto al flujo total. Los resultados gráficos de la aplicación de los algoritmos a los dos ríos en una recesión particular que ocurre después de un evento significativo de precipitación, tanto para el Río de Oro, como para el río Suratá, se muestran en la Fig. 7 y en la Fig. 8. En este caso el evento de lluvia en el Rio de Oro fue de 125 mm en los 5 días anteriores al pico y en Rio Suratá 152 milímetros en 15 días anteriores. En estas gráficas se observa la relación entre el evento de lluvia y el evento del hidrograma, al cual siguen épocas de estiaje importantes (45 días para el caso del río Suratá y 80 días para caso del Río de Oro). Además, en estas figuras, también se puede observar el ajuste al hidrograma de los diferentes algoritmos de separación de flujo base evaluados.
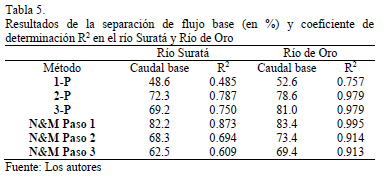
En la Tabla 5 se presentan los resultados obtenidos de porcentaje de separación de flujo base mediante la aplicación de diferentes algoritmos aplicados a las series de tiempo del río Suratá y del Río de Oro.
3.3. Resultados de separación de flujo base
Los porcentajes de error presentados en la Tabla 5 muestran, en general, un resultado más favorable para el ajuste en el Río de Oro que en el río Suratá. Este resultado sugiere que las recesiones analizadas en el Río de Oro, aunque pocas en número, son representativas.
El mayor error para ambos ríos corresponde a la aplicación del algoritmo de un parámetro. Los conceptos analizados y los resultados obtenidos durante este trabajo permiten afirmar que este algoritmo está lejos de representar una estimación confiable para las cuencas en estudio, porque asume una única constante de recesión y desconoce la no linealidad que presenta la relación descarga-almacenamiento del flujo subterráneo en contacto con el río.
Los valores más altos de coeficientes de determinación hallados para los datos de ambos ríos fueron 0.873 y 0.995, con el algoritmo de Nathan & McMahon, paso 1, el cual es considerado como un algoritmo que representa en buena forma el fenómeno de recesión de estos ríos. Los valores más bajos de los errores relativos permiten seleccionar el valor de separación de flujo base de 82.2 % para el río Suratá y 83.4 % para el Río de Oro. Estos son resultados de flujo base que reflejan una componente significativa de flujo subterráneo en ambas cuencas. El parámetro b que corresponde a estos resultados es de 0.875.
Un análisis de sensibilidad realizado a estos resultados muestra que, variando ligeramente el parámetro, los mejores coeficientes de determinación corresponden a un rango de porcentaje de flujo base que varía entre 78 y 82.2% para el rio Suratá y entre 80.5 y 83.4% para el rio de Oro, se seleccionan los que corresponden al valor más alto de R2.
Es importante contar con otras técnicas de separación de flujo base que corroboren los datos obtenidos mediante la aplicación de los algoritmos. Para el caso del Río de Oro, la técnica de isótopos estables reportó un valor de 80 %, casi igual al obtenido mediante los algoritmos numéricos. Hasta el momento no existe otra técnica aplicada que permita contrastar el valor obtenido para el río Suratá.
4. Conclusiones
El estudio de las curvas de recesión en la parte alta de las cuencas del río Suratá y el Río de Oro permitió obtener curvas maestras de recesión que no se ajustan a la forma lineal de la relación almacenamiento-descarga atribuida a un reservorio lineal, en ninguno de los dos casos. Para representar los datos de recesión de estas cuencas fue necesario adicionar un exponente a la ecuación clásica que representa el reservorio lineal. El exponente encontrado, de 0.4, para el Río de Oro, expresa acuíferos libres en contacto con el río y flujos subterráneos en geologías complejas. El exponente de 0.7 para el río Suratá expresa transición entre un acuífero confinado y un acuífero libre.
La constante de proporcionalidad de la relación almacenamiento-descarga fue obtenida, para la cuenca del río Suratá, con un valor (150) bastante cercano a otras cuencas en el mundo que tienen aproximadamente la misma área. Sin embargo, el valor obtenido para el Río de Oro (380) dista de los valores encontrados en otras cuencas. El valor obtenido correspondería a valores encontrados en cuencas con áreas mayores. Acorde con este resultado, la cuenca del Río de Oro (cuya área es de 80 km2) presenta tiempos de viaje promedio de 150 días, que son mayores que los que presenta la cuenca del río Suratá (53 días), con un área de 690 km2. Este resultado puede ser interpretado como una evidencia más de que en la cuenca del Rio de Oro existen flujos subterráneos de largas distancias provenientes de otras cuencas.
Los valores de las constantes de recesión en estas cuencas no se pueden representar con un solo valor, sino con un rango amplio, los valores altos expresan respuesta rápida a la descarga del flujo subterráneo proveniente de recargas locales y los valores bajos expresan una respuesta lenta, característica de recargas de larga distancia. Las recargas locales estarían asociadas a eventos de lluvia de corto plazo, y las recargas de larga distancia lo están a eventos de lluvia de largo plazo.
El algoritmo de Nathan & McMahon fue seleccionado en ambas cuencas porque se acopla bastante bien al hidrograma en épocas de recesión y presenta el mejor ajuste; así, se obtuvo para el Río de Oro, un porcentaje de flujo base de 83.4 %, y para el río Suratá de 82.2 %. El resultado de flujo base del Río de Oro se ha podido corroborar con el resultado obtenido mediante la técnica de isótopos estables (80 %). Los valores de flujo base en ambos ríos expresan una reserva de flujo subterráneo importante. Estos resultados deben ser tenidos en cuenta en la realización de planes de ordenamiento y otorgamiento de licencias ambientales, particularmente en cuencas donde se realizan actividades que afectan el flujo subterráneo como es la minería en la cuenca del Rio Suratá. Se recomienda continuar con el estudio de los fenómenos de flujo subterráneo de manera que sea posible identificar zonas de recarga para su protección.
Los algoritmos numéricos o filtros utilizados han incorporado elementos que incluyen una base física y son una herramienta útil para realizar la separación de flujo base, estos resultados siempre deben ser contrastados con resultados obtenidos utilizando otras técnicas, por ejemplo, la aplicación de isótopos estables del agua.
Bibliografía
[1] IAEA. Isotopic age and composition of streamflow as indicators of groundwater sustainability. Results of a 2004-2009 Coordinated Research Project. 261 P., 2010. [ Links ]
[2] Wittenberg, H. and Sivapalan, M., Watershed groundwater balance estimation using streamflow recession analysis and baseflow separation. Journal of Hydrology, 219, pp. 20-33, 1999. [ Links ]
[3] Sophocleous, M., Interactions between groundwater and surface water: The state of the science. Hydrogeology Journal, 10, pp. 52-67, 2002. DOI: 10.1007/s10040-001-0170-8 [ Links ]
[4] Sánchez-Murillo, R., Brooks, E.S., Elliot, W.J., Gazel, E., Boll., J. Baseflow recession analysis in the inland Pacific Northwest of the United States. Hydrogeology Journal, 23, pp. 287-303, 2015. DOI: 10.1007/s10040-014-1191-4 [ Links ]
[5] Sloto, R.A. and Crouse, M.Y., HYSEP: A computer program for streamflow hydrograph separation and analysis, Water-Resources Investigations Report 96-4040, U.S. Geological Survey, Lemoyne-Pennsylvania, 1996, 46 P. [ Links ]
[6] Rutledge, A.T., Model-estimated ground-water recharge and hydrograph of ground-water discharge to a stream, Water-Resources Investigations Report 97-4253, U.S. Geological Survey, Reston-Virginia, 29 P. 1997. [ Links ]
[7] Rutledge, A.T., Computer programs for describing the recession of ground-water discharge and for estimating mean ground-water recharge and discharge from streamflow records-update, Water-Resources Investigations Report 98-4148, U.S. Geological Survey, Reston-Virginia, 43 P., 1998. [ Links ]
[8] Lim, K.J., Engel, B.A., Tang, Z., Choi, J., Kim, K.-S., Muthukrishnan, S. and Tripathy, D., Automated web GIS based hydrograph analysis tool, WHAT. JAWRA Journal of the American Water Resources Association, 41, pp. 1407-1416, 2005. DOI: 10.1111/j.1752-1688.2005.tb03808.x [ Links ]
[9] Eckhardt, K., How to construct recursive digital filters for baseflow separation. Hydrological Processes, 19, pp. 507-515, 2005. DOI: 10.1002/hyp.5675 [ Links ]
[10] Arnold, J.G., Allen, P.M., Muttiah, R., Bernhardt, G., Automated base flow separation and recession analysis techniques. Ground Water, 33, pp. 1010-1018, 1995 [ Links ]
[11] Chapman, T., A comparison of algorithms for stream flow recession and baseflow separation. Hydrological Processes, 13, pp. 701-714, 1999. [ Links ]
[12] Furey, P. and Gupta, V., A physically based filter for separating base flow from streamflow time series. Water Resources Research, 37, pp. 2709-2722, 2001. [ Links ]
[13] Jakeman, A. and Hornberger, G., How much complexity in warranted in a rainfall-runoff model. Water Resources Research, 29(8), pp. 2637-2649, 1993. [ Links ]
[14] Gómez, S., Aguas subterráneas en zonas de montaña y trazadores ambientales, Bucaramanga, Universidad Industrial de Santander, ISBN 978-958-8777-77-1, 2014. [ Links ]
[15] Cantafio, L. and Ryan, M., Quantifying baseflow and water-quality impacts from a gravel-dominated alluvial aquifer in an urban reach of a large Canadian river, Hydrogeology Journal, 22(4), pp. 957-970, 2014. DOI: 10.1007/s10040-013-1088-7 [ Links ]
[16] Gómez, D. y Gómez, L., Separación de flujo base en la cuenca del Río de Oro en la estación Conquistador alto mediante la programación de algoritmos de no linealidad, Tesis de grado, Escuela de Ingeniería Civil, Universidad Industrial de Santander, Bucaramanga-Colombia, 2012. [ Links ]
[17] Chow, V., Maidment, D. and Mays, L., Applied hydrology, New York, McGraw-Hill, 1998. [ Links ]
[18] Wittenberg, H., Baseflow recession and recharge as nonlinear storage processes. Hydrological Processes, 13, pp. 715-726, 1999. [ Links ]
[19] Griffiths, G.A. and Clausen, B., Streamflow recession in basins with multiple water storages. Journal of Hydrology, 190, pp. 60-74, 1997. [ Links ]
[20] Moore, R., Storage-outflow modelling of streamflow recessions, with application to a shallow-soil forested catchment. Journal of Hydrology, 198, pp. 260-270, 1997. [ Links ]
[21] Tallaksen, L.M., A review of baseflow recession analysis. Journal of Hydrology, 165, pp. 349-370, 1995. [ Links ]
[22] Coutagne, A., Etude générale des variations de débits en fonction des facteurs qui les conditionnent, 2ème partie: Les variations de débit en période non influencée par les precipitations. La Houille Blanche, 3, pp. 416-436, 1948. [ Links ]
[23] Brodie, R. and Hostetler, S., A review of techniques for analysing baseflow from stream hydrographs, Australian National University. 2005. [ Links ]
[24] Gómez, S. and Guzmán, J., Separación de flujo base en la Cuenca superior del río Lebrija. Revista de la Facultad de Ingeniería de la Universidad de Antioquia, 61, pp. 41-52, 2011. [ Links ]
[25] Chapman, T. and Maxwell, A., Baseflow separation - comparison of numerical methods with tracer experiments. 23rd Hydrology and Water Resources Symposium, Hobart-Austria, 1996. [ Links ]
[26] Lyne, V.D. and Hollick, M., Stochastic time-variable rainfall-runnof modelling, in Hydrol and Water Resour. Symp. Institution of Engineers Australia, Perth, pp 89-92, 1979. [ Links ]
[27] Boughton, W., A hydrograph-based model for estimating the water yield of ungauged catchments, Engineering for Hydrology and Water Resources Conference, Newcastle, pp. 317-324. 1993. [ Links ]
[28] Nathan, R. and McMahon, T., Evaluation of automated techniques for base flow and recession analyses. Water Resources Research, 26(7), pp. 1465-1473, 1990. [ Links ]
[29] Ruiz, J.D, y Arenas, J.P., Estudio de la variación del régimen de lluvias en la Cuenca superior del Rio Lebrija. Tesis de Ingenieria Civil. Universidad Industrial de Santander, Colombia, 2005. [ Links ]
[30] Lozano, J., Caracterización del perfil de meteorización de las rocas cristalinas en la cuenca superior del río Lato y sus implicaciones hidrogeológicas, Piedecuesta Santander, Tesis de grado de Geologia. Universidad Industrial de Santander, Colombia, 2012. [ Links ]
[31] Ward, D., Goldsmith, R., Jimeno, A., Cruz, J., Restrepo, H. y Gómez, E., Mapa Geológico del Cuadrángulo H12 Bucaramanga, INGEOMINAS, Bogotá D.C, 1977 [ Links ]
[32] Velandia, F., Gómez, S., Cetina, M. y Castellanos, E., Análisis de fracturas como base para estudios hidrogeológicos alrededor de páramos macizo de Santander, Charta-Colombia. Submitted to: Revista Mexicana de Ciencias Geológicas, 2015 [ Links ]
[33] INGEOMINAS, Proyecto de investigación geológica e hidrológica en la región central del departamento de Santander, 2007. [ Links ]
[34] Oviedo, R., Gómez, S., Hernández, D. y Castillo, E., Análisis de la calidad del agua subterránea en el macizo de Santander al oriente de Bucaramanga. V Congreso Colombiano de Hidrogeología, Medellín, 2014. [ Links ]
[35] Forero, J., Modelo hidrológico distribuido de la cuenca superior del Río de Oro, Tesis de MSc., Escuela de Ingeniería Civil, Universidad Industrial de Santander, Bucaramanga, Colombia, 2012. [ Links ]
[36] Gómez, S. y Anaya, A., Acercamiento a un modelo conceptual de recarga de los acuíferos de la región de Bucaramanga. Revista Avances en Recursos Hidráulicos, 11, pp. 37-50, 2004. [ Links ]
[37] Gómez, S., Taupin, J. y Rueda, J., Estudio hidrodinámico e isotópico de las formaciones acuíferas de la región de Bucaramanga (Colombia), Revista Peruana Geo-Atmosférica, 4, ISSN 2077-3447, 2015. [ Links ]
[38] Arias, C., Gallego, A. y Sana, C., Separación del flujo base utilizando isótopos estables del agua en la cuenca alta del Río de Oro, en la estación El Conquistador Alto, Tesis de grado, Escuela de Ingeniería Civil, Universidad Industrial de Santander, Bucaramanga, Colombia, 2015. [ Links ]
[39] Kottegoda, N. and Rosso, R., Applied statistics for civil and environmental engineers, Oxford, Blackwell Publishing LTDA, 2008 [ Links ]
[40] Wittenberg, H., Nonlinear analysis of flow recession curves, in FRIEND: Flow regimes from international experimental and network data, International Association of Hydrological Sciences IAHS publication No. 221, 1994. [ Links ]
S. Gómez-Isidro, es Ing. Civil de la Universidad Industrial de Santander, Colombia, MSc. en Recursos Hídricos y Dra. en Ingeniería, de la Universidad Nacional de Colombia, sede Medellín, Colombia. Actualmente es profesora titular de la Universidad Industrial de Santander, donde trabaja desde 1991. Es Directora del grupo de investigación en recursos hídricos y saneamiento ambiental - GPH en la Universidad Industrial de Santander. ORCID: 0000-0002-9200-6586.
V.L. Gómez-Ríos, es Ing. Civil de la Universidad Industrial de Santander, Colombia. Ingeniera en proyectos de investigación del grupo GPH -UIS. ORCID: 0000-0001-5975-8201.