Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.197 Medellín maio/jun. 2016
https://doi.org/10.15446/dyna.v83n197.47579
DOI: http://dx.doi.org/10.15446/dyna.v83n197.47579
Effects of joints and their waterstops on pressures spread over a slab subject to turbulent flow on a horizontal apron
Efectos de las juntas y sus sellos en las presiones distribuidas en una losa sujeta a flujo turbulento en un canal horizontal
Mauricio González-Betancourt a & Lilian Posada-García b
a Grupo del Posgrado en Aprovechamiento de Recursos Hidráulicos, Universidad Nacional de Colombia. Investigador financiado por el Fondo Francisco Jose de Caldas (COLCIENCIAS) y SENA, Colombia. magonzalezb@sena.edu.co
b Facultad de Minas, Universidad Nacional de Colombia, Colombia. lilianposadagarcia3@gmail.com
Received: November 29th, 2014. Received in revised form: July 14th, 2015. Accepted: January 25th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
Analyses of measured pressures using multiple sensors above and below a slab subject to supercritical flow and hydraulic jump are presented. Pressures were measured in a physical model constructed in the Hydraulic Laboratory of the Universidad del Valle in Cali, Colombia. Details such as expansion joints, waterstops, slab thickness, and soil-slab separation were simulated. Inflow was full and partially developed, with Froude numbers ranging from 2.84 to 11.6. The role of the expansion joints and waterstops in the generation of uplift pressure and hydraulic gradient below the slab were identified using pressure fields above and below the slab, in multiple tests. The results of this research are critical for the design of bottom slabs in hydraulic structures, which are required to withstand uplift forces and prevent internal erosion problems.
Keywords: uplift pressure, hydrodynamics uplift, slabs, hydraulic model, stilling basins.
Resumen
Se presentan los análisis de las presiones medidas con múltiples sensores sobre y debajo de una losa bajo flujo supercrítico y salto hidráulico. Las presiones fueron medidas en un modelo físico construido en el laboratorio de Hidráulica de la Universidad del Valle en Cali, Colombia. Se simularon detalles como las juntas de expansión, los sellos, el espesor de la losa y la separación suelo-losa. El flujo incidente fue total y parciamente desarrollado con números de Froude entre 2,84 y 11,6. A través de los campos de presión sobre y debajo de la losa de múltiples pruebas, se identificó el papel de las juntas de dilatación y sellos en la generación de presiones de levantamiento y el gradiente hidráulico debajo de la losa. Los resultados de esta investigación son fundamentales para el diseño de losas de fondo en las estructuras hidráulicas que deben soportar las fuerzas de levantamiento y prevenir problemas de erosión interna.
Palabras clave: Presiones de levantamiento, levantamiento hidrodinámico, losas, modelo hidráulico, tanques de amortiguación.
1. Introduction
In interaction with turbulent flow, cavitation, abrasion, uplift force and internal erosion may singly, or jointly, cause the failure of floor slabs in hydraulic structures. The first two processes attack the slab on the face that is exposed to flow. The impact of vapor bubbles and sediments causes random damage to waterstops, allowing static and dynamic pressures to propagate below the slab through cracks or joints. This propagation creates a pressure differential between the top and underside of the slab, which in turn produces uplift force. Other effects of pressure propagation are that the hydraulic gradient below the slab generates internal erosion that manifests through the migration of soil particles and the consequent creation of foundation voids. The fluctuation of uplift pressure and internal erosion induces vibrational movement and offset between slabs. These combined factors bring the slab to failure by causing fatigue of the anchor [1], stagnation pressures [2] and displacement of the slab by the flow.
Uplift pressures has attracted the attention of engineers since the early 1960s, because hydraulic structures subjected to supercritical flow (SF) or to hydraulic jump (HJ) have failed with a flow rate much lower than the design flow rate. For example, damage in spillways, stilling basins or discharge channels was reported in the Big Sandy, Dickinson (USA; [3]), Tarbela (Pakistan; [4]), Karnafulli (Bangladesh; [5]) and Malpaso dams (Mexico; [6]). Other cases of vulnerability to failure were identified in the Scofield (USA; [7]), Santa Elena (Brazil; [8]), Bhakra (India; [9]), Liu-Xia Jia and Qiang Wu-xi dams (China; [10]), cases in which the importance and relevance of uplift force eventually became apparent as a structural design problem.
The role of uplift force in HJ has been studied by taking force or pressure measurements in physical models in order to determine the expected uplift force on the prototype, using Froude scaling relationships ([11-16]). However, as a result of the complexity involved in studying uplift force phenomena, up to now the criteria have failed to take into account many of the variables that affect the uplift pressure and slab thicknesses into the physical and conceptual models used. One influencing factor was that prototype parts were not reproduced or simulated in their true scale in the models; this includes expansion joints, waterstops, slab thickness (s) and slab-soil separation (d). Moreover, in some cases the study of the uplift force below the slab has been limited to taking measurements using pressure taps at the floor of the flume ([11-13, 15]) or force sensors in the central part, below a thin plate which simulates the slab ([14, 16]). These cases do not take into consideration the effects of friction in the joint and below the slab. The flaws inherent in these conceptual models make it difficult to choose criteria that guarantee the stability of the slab at lowest cost. Consequently, designers generally choose the most conservative criteria, which in turn increases costs.
In recognition of these limitations in previous studies, investigations were initiated at the Fluids and Hydraulics Laboratory of the Universidad del Valle, Colombia, in order to verify del Risco's hypothesis [17], which deals with the conversion of kinetic energy into dynamic pressure in expansion joints. For this study a physical model of a slab with multiple sensors and joints was designed [18], and preliminary explorations of the mean pressure below the slab with undeveloped inflow were performed [18-20]. Specifically, with SF, it was considered essential to analyze the effect of transverse and longitudinal joints separately. The results showed that with SF the measured pressures were higher than the static pressures below the slab, which corroborated the conversion of kinetic energy into dynamic pressure in the joint. Moreover, a pattern of pressure in flow direction below the slab was identified: increasing with open longitudinal joints [20] and decreasing with the open transverse joints [19]. It was also found that d inversely affects the value for pressure below the slab [19, 20].
Building on the findings of previous studies, this paper provides a more detailed analysis that presents the pressures measured using multiple sensors above and below a simulated slab with SF and HJ. The pressures spread over a slab were analyzed to find the effect of joints and their waterstops on uplift pressure and the hydraulic gradient below the slab. The work was characterized by: 1) analyzing pressure fields spatially in the time domain, 2) situating sensors below the slab and the joints in order to achieve a higher resolution of the pressure field, 3) considering multiple tests including physical and hydrodynamic variations, 4) identifying the critical hydraulic gradient below the slab to help in assessing internal erosion risks.
2. Materials and methods
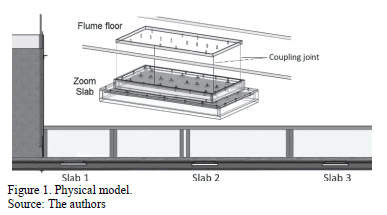
The study was conducted in a horizontal flume (0.5 m high, 8m long and 0.35 m wide) at the Universidad del Valle, using a model that simulated a floor slab and joints. The expansion joints were simulated using an array of acrylic boxes with dimensions from largest to smallest (Fig. 1).
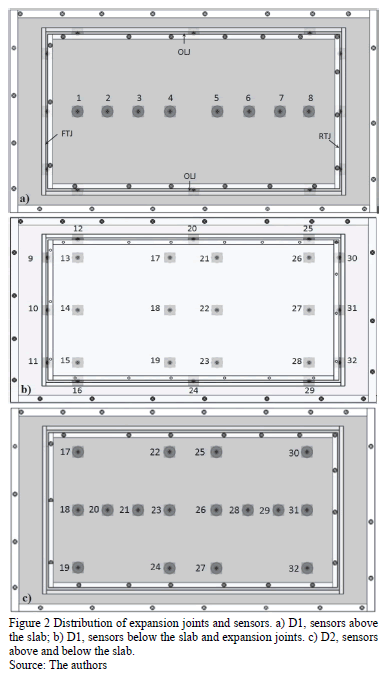
In the model, pressure was measured using 32 circular pressure taps (S1-S32), 2 mm in diameter, above and below the slab. There were two distributions of sensors. The first (D1) selected 8 pressure taps located above the slab (Fig. 2a) and 24 pressure taps below it, as well as the floor of the joints (Fig. 2b). The second (D2) selected 16 pressure taps above and below the slab with equal distribution (Fig. 2c). D1 located sensors below the slab and the joints so that a higher resolution for the pressure field could be achieved.
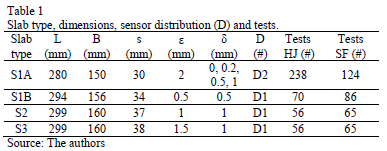
The experimental design included three slabs that were placed in the flume at different distances from the load tank, in order to vary the state of development of the boundary layer of the inflow. Thus, slab 1 (S1) was located at a distance in which Reynolds number in the boundary layer (Rex) was between 300,000 and 660,000 (partially developed flow), slab 2 (S2) was located in the area where Rex was between 4,150,000 and 9,130,000, while slab 3 (S3) was the farthest from the load tank, with Rex between 7,900,000 and 17,380,000.
The length (L) of individual slabs ranged between 6 and 12 times the depth of the inflow (y1); slab width (B) was approximately half L. Geometric variations in the model of d and joint width ( e) were also performed (Table 1), in order to consider their influence on uplift pressure and hydraulic gradient below the slab. In the prototype, these were changed by rearranging the slabs, which could be linked to internal erosion or other sources of natural movement. In the model, d could be adjusted by interposing aluminium sheet rings of 1 mm diameter with the thickness required to achieve the desired separation between slab and background. Joint width was changed by varying the size of the acrylic boxes.
Pressure was measured using Motorola sensors (MPXV 4006GC7U, range 0-6 kpa and accuracy ±5 %) in a range of different tests, which included physical and hydrodynamic variations. In each test, the slab type (S1A, S1B, S2 and S3; Table 1), number of open joint(s), d, flow type (SF or HJ) and Froude number of the inflow (Fr1), was selected. The open joint(s) in S1B, S2 and S3 were simulated by detaching the waterstop(s) in: a) one of the four joints, that is, drawn from either the front transverse joint (FTJ), the rear transverse joint (RTJ) or the longitudinal joint (OLJ); b) any two joints simultaneously, that is, drawn from either the longitudinal joints (LJ) or the transverse (TJ); c) in all joints (AJ). In S1A TJ, LJ or AJ were open. Hydrodynamic variations included a minimum seven different Fr1 between 2.84 and 11.6 for each physical variation.
The discharge was regulated to between 8.15 and 14.1 Gallon/min and vertical gate of the load tank (1.8m high, 1m long, 0.35 m wide) was regulated to between 2.5 and 5.5 cm. The velocities of the inflow (V1) ranged between 1.65 and 5.76 m/s with a turbulent flow regime (Reynolds numbers of 90,000 to 200,000). The flow rate was measured with a Prandtl tube at a point located 0.05 m upstream of the FTJ, with an accuracy of 4%. Discharge was measured using an Omega brand flow meter (FMG-901). Rectangular weirs of heights ranging from 5 to 20 cm placed in the end of the flume were used to generate HJ. Some tests of S1 was formed submerged hydraulic jump (SHJ) and others a free hydraulic jump (FHJ). Tests with FHJ were located with 30% of their length on the slab, because in general the highest pressure fluctuations are reported in the first third of the length of the HJ [13,15,21-27].
The problem of alignment, acknowledged by some researchers [16,28-30], was controlled by maintaining a static slab in the model without the possibility of failure or displacement. Offset between slabs was avoided since that would have increased the uplift pressure below the slab by stagnation points [2,3]. Thus, the slab was part of the flume floor, which was drilled and slotted to provide continuity to pressure taps and joints. The coupling between elements of the system was monitored and the offset was of the order 10-5m. In the prototype, this might have occurred as a result of imperfections in the finishes of the slabs and because of natural movement.
Flow depth was measured with depth gages of range 300 mm, accuracy of ± 0.2 mm on a) FTJ, b) LJ in the middle of the slab; c) RTJ. At each point the minimum and maximum depths detected in 30 second were measured. The average static pressure below the slab (pe) was calculated as the average of the pressure equivalent of three minimum depths measured on FTJ, LJ, RTJ with baseline below the slab.
The sensors were calibrated to relate their voltage signs with the pressures, in accordance with the reference [31]. The acquired signs with a data acquisition system (DAQ National Instruments, NI SCXI: 1000, 1102B, 1600, 1300) were send to a laptop. The sampling frequency (fs) was 200 Hz limited by the data acquisition system available; in addition, this complied with the sampling theorem (avoiding aliasing) and improves the resolution in the time of the digitized signal (5 ms). Following digitization and analysis of the signal, a digital filter was used to remove frequency components lying outside the phenomenon. Responding to the analysis of the frequency signal and the dynamic characteristics of the pressure measurement system, the cutoff frequency of the digital filter was selected at 10.58 Hz.
Macroturbulent natural phenomena do not display periodicity, so each segment of data acquired makes its own unique contribution. Thus, the degree of accuracy is proportional along the length of test run [32]. The minimum test run time stipulated by authors like Lopardo and Henning is one minute [33]. Fiorotto and Rinaldo [25] and Toso and Bowers [13], however, showed how the pressure coefficient increased over time. In the case reported here, the length of the test run was 15 minutes, data acquisition being performed during the last five minutes. The duration of the data acquisition time was associated principally with extensive data and the number of tests explored (760; Table 1). One test had 60,000 pressure fields.
3. Results and analysis
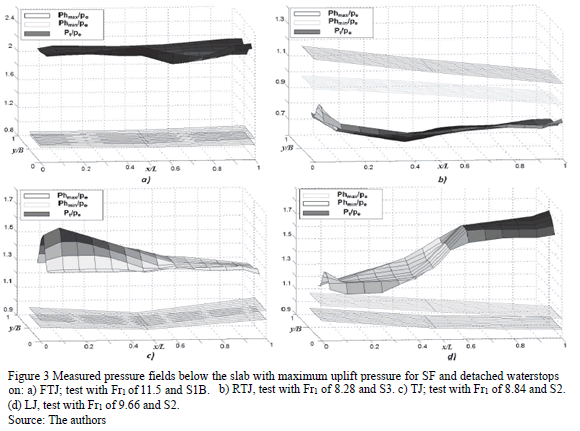
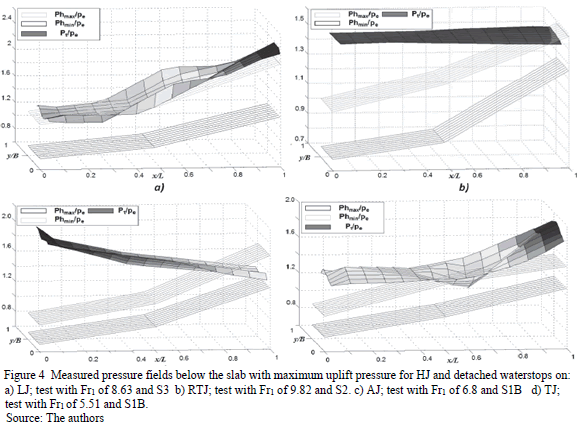
Figs. 3 and 4 represent 3D snapshots of the measured pressure fields below the slab with maximum uplift pressure for SF (Fig. 3) and HJ (Fig. 4), respectively, where, "Pt/pe" is the relationship between the measured pressure (Pt; static and dynamic pressure) and the average static pressure (z axis, Fig.s 3 and 4). "Phmin/pe" and "Phmax/pe" represents the relationship between the pressure equivalent to minimum and maximum depth measured at FTJ, LJ or RTJ and pe (z axis, Fig.s 3 and 4). The pressures were calculated with a baseline that lay below the slab. The positions below the slab are represented on the x axis (length) and y axis (width), which are dimensionless with length (L).
For SF (Fig. 3) a linear correlation of pressure in the direction of flow was observed when waterstops were detached from joints. The negative gradient (Fig. 3c) was favored with TJ or AJ, while the positive gradient (Fig. 3d) was favored with LJ. When there was only one open joint (FTJ, OLJ, RTJ) uniform pressure below the slab was observed (Figs. 3a and 3b). FTJ amplified the static pressure (Fig. 3a) and RTJ decreases it (Fig. 3b).
Under HJ (Fig. 4), the positive pressure correlation is given by the flow; however pressure below the slab can vary depending on the detached waterstops. During tests it was found that, with only one waterstop detached on FTJ, the pressure generated below the slab was uniform (Fig. 4b), while with two open transverse joints (TJ) the positive gradient (Fig. 4a, Fig. 4d) might become altered, in some instances leading to negative pressure gradients(Fig. 4c).
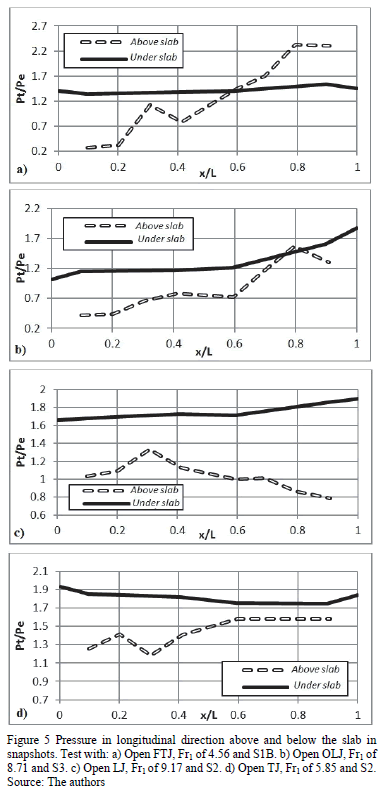
The pressures measured simultaneously above and below the slab with HJ and with detached waterstops on joints, were analyzed. It was observed that the joints acted as a filter of the pressures generated in the flume. Pressure only propagated below the slab at those points located on joints without waterstops. The pressures in direction of flow in one snapshot, and in four other tests, are shown in Fig. 5. It is apparent that some pressure fluctuations above the slab (dotted line) were not perceived below it (continuous line). Furthermore, pressure was not uniform above and below the slab.
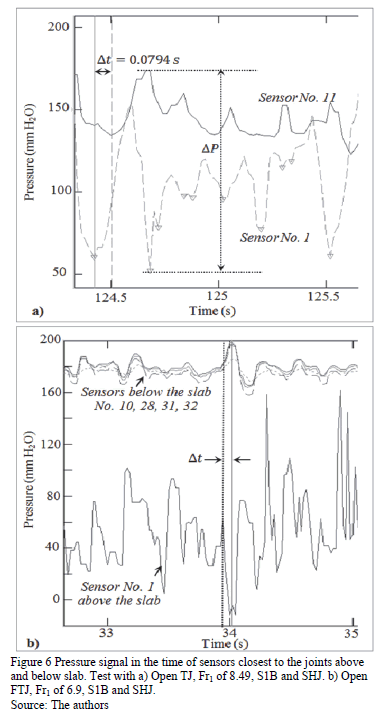
In the tests with HJ, open FTJ and open TJ, a travel time delay was found between the entry of the pressure waves at the joint and their arrival below the slab (Dt). This led to pressure differential (Dp) above and below the slab, which generated high uplift force. To make this evident, in Fig.6, two tests are presented to show the unfiltered signal from pressure sensors close to the open transversal joints above and below the slab. The time delay ranged from 69 to 100ms between the arrival of the pressure pulse at a sensor above the slab (S1) and the one below it (S10, S11, S28, S31). Interchannel delay between S1 and S32 of data acquisition system was estimated at 0.093 ms. This was depreciable against the sampling period (5ms). With open FTJ, a time delay smaller than 5 ms was observed between the unfiltered signals of the sensors below the slab at opposite ends (S10 and S28).
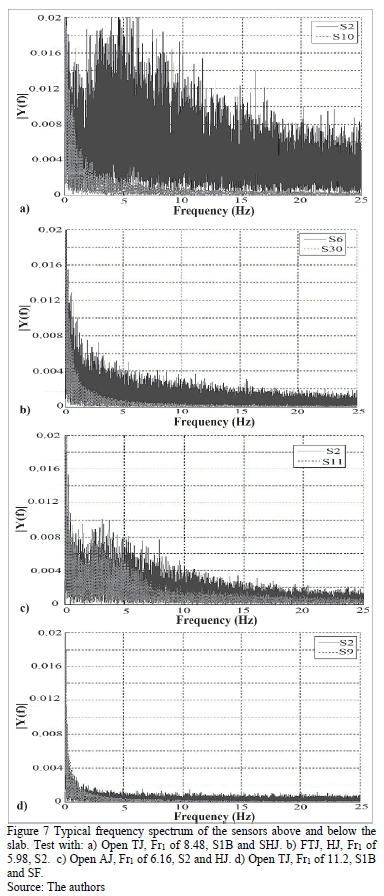
The role of the joints as frequency filters was observed in the comparative analysis of the spectrum of fluctuating pressures between the sensors located above (S2, S6) and below (S9-S32) the slab with SF and HJ (Fig. 7).
The sensors below the slab measured a significant drop in frequency amplitude (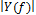 ) on frequencies higher than 6 Hz (Fig. 7). The frequency cutoff of the pressure fluctuation in the flume with HJ has been defined by some authors as 25 Hz [5, 13, and 24]; however this only applies above the slab, because the cutoff frequency would be less than 10 Hz below it. Furthermore, it was observed with SF that joint-flow interaction may increase
) on frequencies higher than 6 Hz (Fig. 7). The frequency cutoff of the pressure fluctuation in the flume with HJ has been defined by some authors as 25 Hz [5, 13, and 24]; however this only applies above the slab, because the cutoff frequency would be less than 10 Hz below it. Furthermore, it was observed with SF that joint-flow interaction may increase 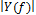 for frequencies lower than 4 Hz (Fig. 7d), when measured below the slab.
for frequencies lower than 4 Hz (Fig. 7d), when measured below the slab.
The system of irregular cavities integrated by the joints, waterstops, and d may be understood as a labyrinth of networked cavities with unpredictable passages, reductions, changes of direction, and dead ends [34]. Thus, when the pressure wave enters the network of cavities through an open joint or missing waterstop, it spreads below the slab and experiences diffraction, interference, reflection and refraction that may alter its propagation velocity, amplitude and the transmitted energy. Furthermore, waterstops, joints and flow determine the configuration of vortices within the joint and in the d, which vary the pressure that is transmitted below the slab.
In HJ, the pressure pulses on the slab were uncorrelated since the slab length is larger than the integral scale of the pressure fluctuations. The integral scale was calculated by Fiorotto and Rinaldo [25] as ranging from 0.4y1 to 1.5y1. The results of the current study showed that extreme pulses recorded by a single sensor in the large slab do not provide a representative sample of the pressure fields above and below the slab and cannot, therefore, be used to calculate the uplift force accurately. Above the large slab, a positive or negative pulse is a local effect. The compensation of the pressure pulses on the upper face of the slab was recognized by Bellin and Fiorotto [16].
After studying the pressure fields with different open joints, it was shown that pressure distribution was not uniform below the slab. In other words, a hydraulic gradient was formed.
The hydraulic gradient below the slab generates a drag force on soil particles at d. These particles dislodge from the soil and move in the direction of flow below the slab when the drag force is greater than the interlocking of the soil particles [35,36]. In the tests this dislodgement of particles and one unfiltered exit generated piping along the conduit and a loss of support for the slab [37].
The foundation materials may be eroded into drains and unfiltered systems over long periods of time before they are detected. Therefore, the slab and foundation materials must be designed for a critical hydraulic gradient. Unfortunately at this moment, internal erosion is a potential failure mode that cannot be completely analyzed using numerical formulae or models [35]. However, valuable information on dam and soil behavior, and on experimental hydraulic gradients can be obtained to help assess internal erosion risks.
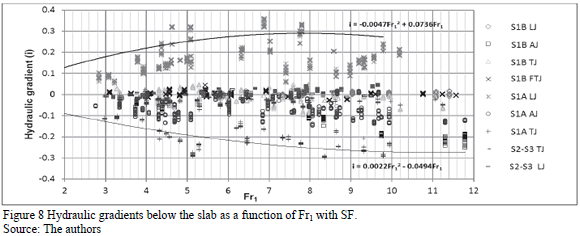
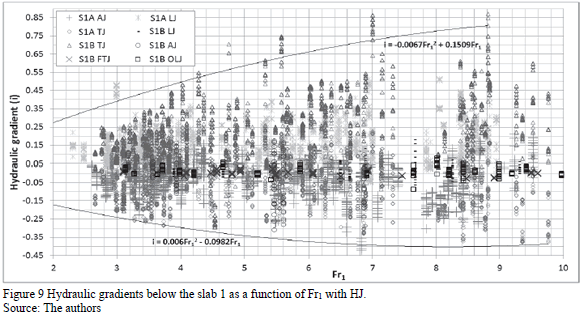
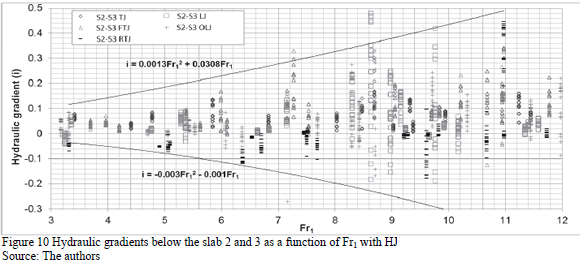
Figs. 8, 9, and 10 present the critical hydraulic gradients below the horizontal slab in multiple tests. These include SF (Fig. 8) and HJ with undeveloped (Fig. 9) and developed (Fig. 10) inflow conditions. The hydraulic gradient (i) was the slope of the piezometric line between the pressure below the slab in proximity to FTJ and RTJ (the ratio between the pressure gradient below the slab and its length). "S1A" collected tests with four variations of d, since its influence was not easy to perceive in the hydraulic gradient. As reference, envelope curves on the maximum hydraulic gradients are plotted in the Figs. 8, 9, and 10.
Critical envelope curves in the evaluation of multiple tests were found with the condition of undeveloped inflow to SF (Fig. 8) and HJ (Fig. 9). The most critical envelope curve was found with undeveloped inflow and HJ (Fig. 9). To establish the design of the hydraulic gradient calculated with envelope curves to SF, the position of HJ should be ensured by controls at the floor of the flume. Slabs installed in sloping flumes should be considered as additional hydraulic gradients established by slab sloping.
The results of the study showed uniform pressurization below the slab with only one open transversal joint. Similar results were found by Melo, Pinheiro and Ramos [38] with slabs exposed to the impact of a jet in the plunge pool. However before considering slab design with open joints as a strategy to reduce uplift pressure with large slabs, the effect of the eccentricity of the uplift force and the likelihood of internal erosion risk should be evaluated. Large slabs are typically used to protect easily erodible materials in the foundation [39]. Therefore, waterstops are required in joints, and these must be maintained if piping, stagnation points, and future rearrangement of the slab are to be avoided.
The results of this study should be incorporated into future design criteria in an effort to optimize costs.
4. Conclusions
In this study it was observed that joints and their waterstops with turbulent flow on a horizontal apron influence the spread of pressure over a slab because:
- Joints and waterstops act as filters of pressure fluctuations generated in the flume. Pressure only propagates below the slab at points located on the joints without waterstops.
- Joints generate a time delay between the entry of the pressure wave at the joint and its arrival below the slab. This leads to a pressure differential between the top and bottom of the slab resulting in the appearance of uplift force.
- The interactions between the joints and the main stream alter the amplitude of the pressure wave below the slab.
- With only one open transversal joint pressure is uniform below the slab.
- With two or more open joints pressure gradients is generated below the slab.
The lack of uniformity in uplift pressure below the slab leads to consider the failure mechanism induced by moment. Therefore, future research is necessary in order to predict net uplift force and its point of application and, as a result, verify instability of the slab by moment of the uplift force.
The hydraulic gradients shown here constitute valuable experimental information that helps to assess internal erosion risks in hydraulic structures.
Acknowledgments
This research project was partially funded by COLCIENCIAS. Special thanks are due to Efraín del Risco for his valuable suggestions and insight in this field. The experiments necessary for the development of this research were carried out at the Hydraulic Laboratory at the University of Valle in Cali, Colombia. The support of the laboratory is sincerely appreciated.
Nomenclature
FTJ Front transverse joint
RTJ Rear transverse joint
OLJ One longitudinal joint
LJ Longitudinal joints
TJ Transverse joints
AJ All joints
D The slab-soil separation
References
[1] Khatsuria, R.M., Hydraulics of spillways and energy dissipators. New York: Marcel Dekker, 2005, pp 411-424. [ Links ]
[2] Frizell, W.K., Uplift and crack flow resulting from high velocity discharges over. Report DSO-07-07 U.S. Department of the interior, Bureau of Reclamation. Denver, Colorado, 2007, pp 2-5. [ Links ]
[3] Hepler, T.E. and Johnson, P.L., Analysis of spillway failure by uplift pressure. ASCE National Conference, Colorado Springs, Colorado, august 8-12, pp 857-862, 1988. [ Links ]
[4] VSL International. Soil and rock anchors, Examples from practice. Berne, Switzerland. [Online]. pp 19-20, 1992 [Consulted: 15th of august of 2009]. Available at: www.vsl.net/Portals/0/vsl_techreports/PT_Ground_Anchors.pdf. [ Links ]
[5] Bowers, C.E. and Tsai, F.Y., Fluctuating pressures in spillway stilling basins. J. Hydraulic Division, ASCE, 95(6), pp. 2071-2079, 1969. [ Links ]
[6] Bribiescas, S. and Capella, V., Turbulence effects on the linning of stilling basins. Proceedings ICOLD. Congrés des Grands Barrages. Madrid. Q.41. R.83. pp. 1575-1592, 1973. [ Links ]
[7] Frizell, K.H., Spillway, outlet works, and water conveyance needs-survey results. Hydraulic laboratory report HL-2005-03. U.S. Department of the Interior, Bureau of Reclamation. Denver, Colorado. pp. 10-30. 2005. [ Links ]
[8] Ivanissevich, M.L., Discussion: Fluctuating uplift and lining design in spillway stilling basins, by Fiorotto, V. and Rinaldo, A., 118(4),April, 1992. Journal of Hydraulic Engineering. 119(4). pp. 526-527, 1993. DOI: 10.1061/(ASCE)0733-9429(1993)119:4(526) [ Links ]
[9] Ramos, C.M., Models for study of the hydrodynamic actions on hydraulic structures. Recents advances in Hydraulic Modelling. Kluwer Academic Publishers, Netherlands. Series E: Applied Science, 165, pp. 143-189, 1989. DOI: 10.1007/978-94-009-2344-7_4 [ Links ]
[10] Liu, P-Q. and Li, A-H., Model discussion of pressure fluctuations propagation within lining slab joints in stilling basins, Journal of Hydraulic Engineering, 133(6), pp. 618-624, 2007. DOI: 10.1061/(ASCE)0733-9429(2007)133:6(618) [ Links ]
[11] Bribiescas, S. y Fuentes, O., Tanques amortiguadores. Reporte Técnico, Proyecto 7045. UNAM, México D.F. pp. 1-50, 1978. [ Links ]
[12] Hajdin, G., Contribution to the evaluation of fluctuation pressure on fluid currents limit areas- based on the pressures recorded at several points of the area. VIII Conference of Yugoslav Hydraulics Association, Portoroz. 1982. [ Links ]
[13] Toso, J. and Bowers, C., Extreme pressures in hydraulic-jump stilling basins, J. of Hydraulic Engineering, 114(8), pp. 829-843, 1988. DOI: 10.1061/(ASCE)0733-9429(1988)114:8(829) [ Links ]
[14] Farhoudi, J. and Narayanan, R., Force on slab beneath hydraulic jump. J. of Hydraulic Engineering, 117(1), pp. 64-82, 1991. DOI: 10.1061/(ASCE)0733-9429(1991)117:1(64) [ Links ]
[15] Mees, A., Estudo dos esforços hidrodinâmicos em bacias de dissipação por ressalto hidráulico com baixo número de Froude. MSc. Thesis. Universidade Federal do Rio Grande do Sul, Porto Alegre, Brasil. 2008. [ Links ]
[16] Bellin, A. and Fiorotto, V., Direct dynamic force measurements on slab in spillway stilling basin. J. of Hydraulic Engineering. 121(10), pp. 686-693, 1995. DOI: 10.1061/(ASCE)0733-9429(1995)121:10(686) [ Links ]
[17] del Risco, E., Inestabilidad del revestimiento del fondo de un tanque amortiguador. PhD dissertation, Faculty of Engineering. UNAM, México D.F., México, 1989. [ Links ]
[18] del Risco, E., Estudio del Levantamiento de una losa de revestimiento. Technical Report, Faculty of Engineering, Universidad del Valle, Cali, Colombia. pp. 2-4, 2006. [ Links ]
[19] del Risco, E., Hurtado, E. y González, M., Estudio experimental de las presiones de levantamiento bajo una losa con juntas transversales al flujo. Tecnología y Ciencias del Agua. I(1), pp. 31-42, 2010. [ Links ]
[20] Hurtado, E., del Risco, E. y González, M., Presiones medidas en la base de una losa de fondo con juntas paralelas al flujo en un canal. Revista de la Facultad de Ingeniería de la Universidad de Antioquia, 47, pp. 39-52, 2009. [ Links ]
[21] Vasiliev, O.F. and Bukreyev, V.I., Statistical characteristics of pressure fluctuations in the region of hydraulic jump. Proceedings 12th IAHR Congress, Fort Collins, USA. 1967. [ Links ]
[22] Pinheiro, A., Accoes hidrodinámicas em bacias de dissipacao de energia por ressalto. PhD. dissertation, Universidad Técnica de Lisboa, Lisboa, Portugal, 353 P., 1995. [ Links ]
[23] Khader, M. and Elango, K., Turbulent pressure field beneath a hydraulic jump. J. of Hydraulic Research, 12(4), pp. 469-489, 1974. DOI: 10.1080/00221687409499725 [ Links ]
[24] Fiorotto, V. and Rinaldo, A., Fluctuating uplift and linnings design in spillway stilling basins. J. Hydraulic Enginnering ASCE. 118(4), pp. 578-596. 1992a. DOI: 10.1061/(ASCE)0733-9429(1992)118:4(578) [ Links ]
[25] Fiorotto, V. and Rinaldo, A., Turbulent pressure fluctuations under hydraulic jumps. J. of Hydraulic Research, 130, pp. 499-520, 1992b. DOI: 10.1080/00221689209498897 [ Links ]
[26] Lopardo, R., de Lio, J. and Lopardo, M., Physical modelling and design estimation of instantaneous pressures in stilling basins. Proceedings of the XXVIII IAHR Congress. Graz. 132 P., 1999. [ Links ]
[27] Hassonizadeh, H. and Shafai-Bajestan, M., Experimental measurement of dynamic force on slab in stilling basins. Wetlands Engineering & River Restoration. Conference Proceeding Paper. Section: 47. Chapter: 4. 2001. DOI: 10.1061/40581(2001)125 [ Links ]
[28] Levi, E. y Masa, J., Estudio sobre la flotación de losas en tanques amortiguadores. Memorias 2do. Congreso Nacional de Hidráulica. Culiacán. México. pp. 147-165, 1972. [ Links ]
[29] Levi, E., and del Risco, E., Search for the cause of high-speed-flume revetment failures, ASCE, J. of Performance of Constructed Facilities, 3(2), 1989. DOI: 10.1061/(ASCE)0887-3828(1989)3:2(125) [ Links ]
[30] del Risco, E., Investigación experimental de la falla de losas de revestimiento de tanques amortiguadores. MSc. Thesis, Faculty of Engineering. UNAM, México D.F., México, 1983. [ Links ]
[31] González, M. y Giraldo, S., Caracterización dinámica de sensores de presión utilizando el principio de la botella de mariotte. Rev. Fac. Ing. Univ. Antioquia, 71, pp. 146-156, 2014. [ Links ]
[32] Tatone, G., Selección de transductores para la medición de presiones fluctuantes. XXIV Congreso Latinoamericano de Hidráulica, Punta del Este, Uruguay. pp. 5-9, 2010. [ Links ]
[33] Lopardo, R.A. and Henning, R.E., Experimental advances on pressure fluctuation beneath hydraulic jumps. Proc., 21st IAHR, Melbourne Australia, Vol. 3, 1985. [ Links ]
[34] González, M., Levantamiento de una losa de piso sometida a un flujo turbulento. PhD Dissertation, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. 2013. [ Links ]
[35] Bureau of Reclamation and USACE. Dam safety risk analysis best practices training manual. U.S. Department of the Interior Bureau of Reclamation, Colorado. Version 2.2, cap. 24, pp. 1-47, 2011. [ Links ]
[36] Hansen, E., Unsteady pressure-driven viscous flows beneath concrete pavement slabs. J. of Hydraulic Engineering, 117(6), pp. 713-724, 1991. DOI: 10.1061/(ASCE)0733-9429(1991)117:6(713) [ Links ]
[37] Trojanowski, J., Water operation maintenance bulletin. Proceedings United States Society on Dams, 26th annual conference in San Antonio, Texas. May. 1-5, No. 218, pp. 2-19, 2006. [ Links ]
[38] Melo, J., Pinheiro, A. y Ramos, C., Forces on plunge pool slabs: Influence of joints location and width. J. of Hydraulic Engineering, 132(1), pp. 49-60. 2006. DOI: 10.1061/(ASCE)0733-9429(2006)132:1(49) [ Links ]
[39] Blair, H.K. and Rhone, T.J., Design of small dams. Bureau of Reclamation, 3a ed., Washington, DC, cap. 9, Spillways structural design details. 1987, pp. 429-434. [ Links ]
M. Gonzalez- Betancourt, was awarded his BSc. Eng in Agricultural Engineering by the Universidad Nacional de Colombia, Palmira, Colombia, and Universidad del Valle, Cali, Colombia, in 2008. He received his PhD. in Engineering with emphasis on Hydraulic Resources in 2014 from the Universidad Nacional de Colombia, Medellin, Colombia. Between 2008 and 2010, he worked at the Hydraulic Laboratory at the Universidad del Valle. Since 2009 he has been associated with the research group "Posgrado en Aprovechamiento de Recursos Hidráulicos" (Postgraduate program on the use of Hydraulic Resources) at the Universidad Nacional de Colombia. From 2014 to date, he has been a researcher in Colombia under the terms of the joint agreement between "Organización de Estados Iberoamericanos" [Organization of Iberoamerican States], "Servicio Nacional de Aprendizaje" [National Apprenticeship Service] and "COLCIENCIAS" [Administrative Department of Science, Technology and Innovation]. ORCID: 0000-0001-5485-8043
L. Posada-García, was awarded his BSc. Eng in Civil Engineering in 1976, by the Universidad Nacional de Colombia, Medellín, Colombia. She was awarded her MSc. in Hydraulic Resources in 1982 and her PhD degree in Civil Engineering in 1995 from Colorado State University, USA. Since 1976, she has been a Professor in the Facultad de Minas, Universidad Nacional de Colombia, Medellín campus, Colombia. ORCID: 0000-0002-5504-2203