Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.197 Medellín maio/jun. 2016
https://doi.org/10.15446/dyna.v83n197.51543
DOI: http://dx.doi.org/10.15446/dyna.v83n197.51543
Thermodynamic properties of moisture sorption in cassava flour
Propiedades termodinámicas de humedad de sorción en harina de yuca
Alfredo A. Ayala-Aponte
Escuela de Ingeniería de Alimentos, Universidad del Valle, Cali, Colombia. alfredo.ayala@correounivalle.edu.co
Received: June 25th, de 2015. Received in revised form: November 6th, 2015. Accepted: December 3rd, 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
Thermodynamic adsorption properties (differential enthalpy and entropy, spreading pressure and net integral enthalpy and entropy) of cassava flour were determined at 25, 30 and 35°C to provide information about the water and energy requirements for the sorption process. The Guggenheim-Anderson-de Boer (GAB), Peleg and Halsey models were found to adequately describe the sorption characteristics, however the Peleg model provided the best fit. The enthalpy and entropy differentials decreased with increased equilibrium moisture content. The spreading pressure increased with increased water activity but decreased with increased temperature. The net integral enthalpy decreased with increased moisture content, with an asymptotic tendency to 0.2920 kJ/mol for a moisture content of 33.4% (d.m). In contrast, the net integral entropy values were negative and increased up to 0.1687 kJ/mol for a moisture content of 29.2% (d.m).
Keywords: adsorption isotherms; mathematical sorption models; thermodynamic sorption properties.
Resumen
Se determinaron propiedades termodinámicas de adsorción (entalpía y entropía diferencial, presión de superficie, entalpía y entropía integral neta) en harina de yuca a 25, 30 y 35°C, para proporcionar información sobre requerimientos de agua y de energía en el proceso de sorción. Los modelos de GAB, Peleg y Halsey fueron los que mejor describieron las características de sorción, siendo el de Peleg el de mejor ajuste. Los diferenciales de entalpia y entropía disminuyeron con el incremento del contenido de humedad de equilibrio. La presión de superficie se incrementó con el aumento de la actividad de agua pero disminuyó con el incremento de temperatura. La entalpia integral neta decreció con el aumento de la humedad con una tendencia asintótica hasta 0.2920 kJ/mol para una humedad de 33.4 % (b.s); mientras que los valores de la entropía integral neta fueron negativos y se incrementaron hasta 0.1687 kJ/mol para una humedad de 29.2 % (b.s).
Palabras clave: isotermas de adsorción; modelos matemáticos de sorción; propiedades termodinámicas de sorción.
1. Introduction
Cassava (Manihot esculenta, Crantz) is a root rich in carbohydrates that is frequently consumed in tropical countries. It is processed in many ways for consumption by humans or animals [1]. In its fresh state, it is composed of approximately 35% carbohydrates, 62% water, 1-2% protein, 0.3% fat, 1-2% fiber and 1% minerals [2]. Due to its high water content, it is a perishable vegetable that requires preservation processes. Drying processes, which are widely applied to food to extend its storage stability, can be used as alternatives to preservation [3, 4]. As a preservation and processing alternative, cassava is transformed into flour after drying; however, to prevent the physicochemical and microbial degradation of the flour, it should be stored under suitable conditions of temperature and relative humidity [1]. Hence, it is important to understand the relationship between aw and the equilibrium moisture content (EMC) of cassava flour (sorption isotherms) and of food in general in order to predict the changes to their physical, chemical and microbiological properties that occur during storage and processing [4]. The sorption isotherm is applicable to the analysis and design of food drying, mixing and packaging, and can be used to determine optimal storage conditions, product shelf-life and proper packaging material [1]. Furthermore, the determination of sorption isotherms at various temperatures provides information about the thermodynamic sorption properties of the food-water vapor system that affects the process, such as the differential enthalpy (isosteric heat of sorption), differential entropy, net integral enthalpy, spreading pressure and net integral entropy. These properties are useful to understand the behavior of water during the food-drying process and to optimize and quantify the energy requirements during mass and heat transfer [2]. They are also useful for providing information about the microstructure, water-sorption kinetics and interpretation of the physicochemical phenomena that occur at the water-solid interface [5]. According to Al-Muhtaseb et al. [6], the thermodynamic properties are also useful for determining the final dehydration point needed to achieve a stable food with the least amount of energy applied.
The differential enthalpy of sorption is useful to estimate the energy requirements for drying, as well as to provide information on the water state in food products. The differential entropy of sorption is proportional to the number of active sorption sites available at a specific energy level [7]. The spreading pressure is associated with the excess of free energy at the surface of the food solid, which means the increase of surface tension in the sorption active sites of water molecules [8,9]. The net integral enthalpy and entropy are used to explain the modes of moisture sorption in food products. The integral enthalpy provides information on the bond strength between water molecules and the solid [9], and the integral entropy describes the degree of disorder or randomness of the movement of water molecules [10]. These thermodynamic properties have been widely studied in many foods, such as potato [8], rice [7], mango powder [11], and starch [12], among others. However, the available literature is scarce for cassava flour. Notable research has been undertaken by Koua et al. [13] and Aviara et al. [2]; these studies were performed at different temperatures and with different varieties than those used in this study. Therefore, the purpose of this study was to determine the thermodynamic sorption properties (differential enthalpy, differential entropy, spreading pressure, net integral enthalpy and net integral entropy) in cassava starch at 25, 30 and 35°C.
2. Materials and methods
2.1. Preparation of the raw material
Cassava (Manihot esculenta, Crantz) roots were used, which were washed with potable water, manually peeled with steel knives, chopped and dried in an oven (MLW, Germany) with forced-air circulation at 65°C until constant weight. The dry parts were ground in a ball mill on a laboratory scale. The flour samples were packaged in polyethylene bags and stored in desiccators containing P2O5.
2.2. Determination of the adsorption isotherms
The adsorption isotherms were determined using a temperature controlled cabinet (Hot Pack, US), with an accuracy of ±1 °C at the selected temperatures of 25, 30 and 35°C using the gravimetric method, according to the COST 90 project [14]. This method consists of applying saturated saline solutions to maintain a given constant value of aw of the flour samples, when equilibrium is achieved between the atmosphere and the food.
Eight saturated saline solutions (LiCl, CHCOOK, MgCl2, K2CO3, NaBr, SrCl2, KCl and BaCl2) were used, which were enclosed in hermetic containers and had aw values that varied between 0.1117 and 0.9017 at various temperatures [15]. Petri boxes with 2.500 ± 0.002 g of cassava flour were introduced into each hermetic container with the corresponding saline solution. Tymol was placed into the containers with saline solutions that had aw values higher than 0.65 to prevent microbial growth. The samples were periodically weighed every three days until a constant weight was achieved, to ensure equilibrium between the samples and the saline solutions. The samples were removed from the containers between the 19th and 25th day. The duration of the periodical weighing of the samples was less than 1 min to avoid any effect on the results. The EMC of the samples was determined using the oven method by AOAC [16]. The adsorption experiments for each temperature were performed in triplicate. The effect of temperature on the equilibrium moisture content was evaluated using analysis of variance (ANOVA) at a significance level of 95%, using the statistical software SPSS 11.
2.3. Modeling of the sorption isotherms
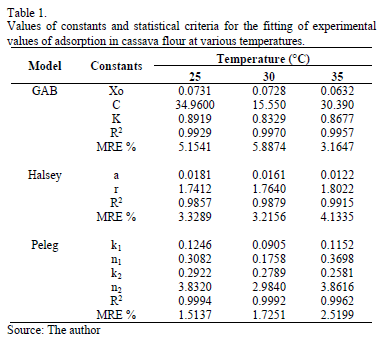
The Guggenheim, Anderson and Boer (GAB) (Eq. 1), Peleg (Eq. 2) and Halsey (Eq. 3) sorption models were used to fit the experimental EMC values.

xo: moisture content of the monolayer
C: Guggenheim constant, a characteristic of the product and related to the heat of adsorption of the monolayer
K: constant related to the heat of adsorption of the multilayer

k1 , k2 , n1, n2: model constants

a and r: model constants
These models are widely used in the literature on food[8, 13, 17, 18]. The model parameters were determined by nonlinear regression using the program MATLAB v7.0. The mean relative error percentage (MRE, %) (Eq. 4) and the coefficient of correlation (r2) were used as criteria to determine the best fit for the experimental sorption values. A model is considered acceptable if values for MRE are below 10% [19] and r2 approaches 1.

Xei: moisture content (g water/g d.m)
Xci: calculated moisture content (g water/g d.m)
N: number of samples
2.4. Determination of the Thermodynamic Properties
2.4.1. Differential enthalpy of sorption
The differential enthalpy of sorption is also called the isosteric heat of sorption (Qst) and is determined from experimental values using the Clausius-Clapeyron equation (Eq. 5):

where qst is the net isosteric heat of sorption, R is the universal gas constant, and l is the latent heat of vaporization of pure water, calculated for the fixed temperature of 30°C (l = 46.011 kJ/mol), corresponding to the average of 25, 30 and 35°C.
By plotting ln(aw) versus 1/T for various EMC values (between 5 and 35 kg water/kg d.m), linear relationships were obtained, with slopes equal to (-(Qst-l/R), from which Qst was calculated.
2.4.2. Sorption entropy
The differential entropy of adsorption (Sd) was calculated by the Gibbs-Helmholtz equation (Eq. 6):

Where G is the Gibbs free energy, calculated using Eq. 7:

By substituting equation (7) into (6), Eq. 8 is obtained:
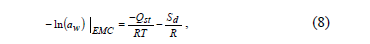
By plotting ln (aw) versus 1/T for a constant water content, the Sd value is calculated from the intercept (Sd/R).
2.4.3. Net integral enthalpy of sorption
The value of the net integral enthalpy (Qin) (Eq. 9) is analogous to the differential enthalpy of sorption, but it is calculated at a constant diffusion pressure. The value Qincan be obtained from the slope of the plot of ln (aw) vs. 1/T:

2.4.4. Spreading pressure
The spreading pressure (Ø) represents the free surface energy for sorption and can be considered to be the difference in surface tension between the active adsorption sites in the solid and the water molecules [8, 9]. Its units are (J/m2). The value Ø is not experimentally determined, but it can be obtained through an analytical procedure related to Eq. 10 [9].

Where q = EMC/x0 ( xo: the moisture in the monolayer).
To avoid undefined values of Ø for aw = 0, the lower limit of aw = 0.05 was taken in Eq. 10. The calculated spreading pressure values were fitted, adding the corresponding value to the range of aw between 0 and 0.05, which was calculated assuming a linear relation (Henry's law) between EMC and aw [9, 20]. Hence, by using an analytical procedure and the Halsey equation (Eq. 3) to describe the empirical relation between EMC and aw, Ø was calculated (Eq. 11). For this, the Halsey equation was substituted into Eq. 10 [2, 8, 20]:
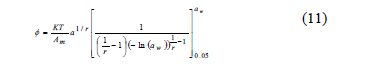
Where r and a correspond to the Halsey equation constants (Eq. 3), and Ø was determined at the three study temperatures (25, 30 and 35°C).
2.4.5. Net integral entropy of sorption
The net integral entropy (Sin) describes the degree of disorder and randomness of the movement of water molecules [10]. It also quantifies the mobility of water molecules adsorbed during sorption [9]. The Sin of a system can be calculated with equation 12 [10], considering that the geometrical mean of activity (aw)* is used, obtained at a constant spreading pressure at various temperatures:

3. Results
3.1. Adsorption isotherms of water
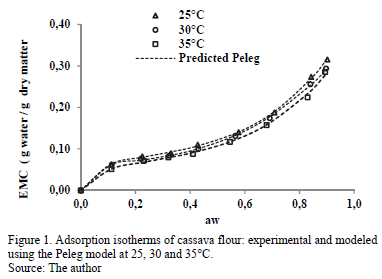
The experimental adsorption isotherms of water from cassava flour at various temperatures are presented in Fig. 1. The samples presented an initial moisture content of 2.621 ± 0.011 g water /g dry matter. The standard deviation of the average EMC values in the adsorption isotherms at the three temperatures varied from 0.02 to 0.08. The isotherms presented a sigmoid shape (inflection point at low aw values), classified as type II according to Brunauer, Deming and Troller, as reported by Iguedjtal [21].
ANOVA indicated significant influence (p<0.05) of the temperature on the EMC, indicating a decrease in EMC with increased temperature in the entire range of aw. This means that cassava flour has lower water retention at higher temperature. In turn, with increased temperature for the same moisture level, aw increases, which may increase the product deterioration rate [22]. Similar results have been observed in the water-adsorption isotherms in certain cassava products [17,23,24]. This influence of temperature on water retention has been attributed to the reduction or loss of active sites where water molecules interact with the surface of the food [25].
3.2. Modeling of the sorption isotherms
Table 1 presents the adsorption parameters, including the MRE and r2 value for the GAB, Halsey and Peleg sorption models for the three temperatures. The three models presented good fits, with MRE values lower than 10% and high r2 values. However, the Peleg model was best because it presented the lowest MRE and MRES values and highest r2 values.
A comparison of the EMC experimental values for cassava flour and those predicted with the Peleg model is presented in Fig. 1. It indicates the good fit of this model along the entire range of aw.
The GAB model has the advantage of providing information about the moisture content at the monomolecular layer or monolayer (xo) (Table 2). The xo value indicates the amount of water that is strongly adsorbed in the active sites of the food, and it is considered to be the value at which the food is most stable during storage [1].
3.3. Thermodynamic properties
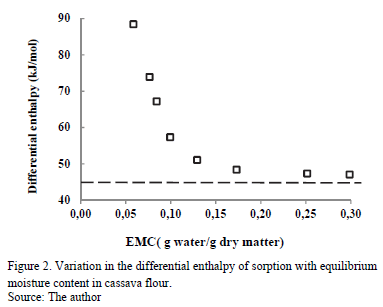
3.3.1. Differential enthalpy of sorption (isosteric heat)
Fig. 2 shows the change in Qst with EMC. Notice that when EMC decreases, Qst increases, ranging from 47.10 to 88.49 kJ/mol for moisture values between 30 and 5.8 g water/g dry matter, respectively. This indicates the strong retention of water molecules in the active sites on the solid phase of the food. According to some researchers [26], the energy interaction level between water and the solid phase at low EMC is higher than the interaction between water molecules at high EMC. Similar behavior was observed in sorption isotherms in various cassava products [17,23,24] and in other foods, such as corn [27], yellow pitahaya [28], plantain pulp [29] and orange powder [18].
In the entire EMC range, Qst is higher than the heat of vaporization of pure water (l(30ºC) = 46.011 kJ/mol, and it has similar values at high EMC. This indicates that the energy of interaction between the water molecules at the adsorption sites (active points) at the surface of the food is higher than the energy at which the molecules of pure water exist in the liquid phase. In the adsorption processes during storage, Qst provides information on the water-solid interaction and the chemical, physical and microbiological state of the food [8].
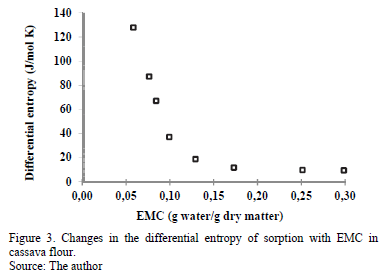
3.3.2. Differential entropy of sorption
Fig. 3 indicates the strong dependence of the differential entropy (DS) on the EMC, with a maximum of 129.0 J/mol·K at an EMC of 0.058 g water/g d.m, past which the value decreases with increasing moisture. This result has been observed in many products, such as potato flakes [30], potato [8], prickly pear [31] and potato starch [12]. The DS value is proportional to the number of active sorption sites at a determined energy level [7]. This means that the number of available sorption sites decreases with increased moisture because these active sites become covered with water molecules, decreasing their mobility. According to certain researchers [32,33], the decrease in the differential entropy with increased moisture is associated with the restriction of the molecular movement of water. According to other researchers [34], the differential entropy can be used to understand the moisture adsorption process associated with dilution and crystallization. Rotstein [35] argues that DS can be used in an energy balance, providing information on the energy use in food processing.
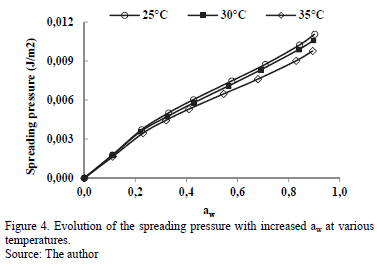
3.3.3. Spreading surface
The evolution of spreading pressure (Ø) with temperature is presented in Fig.4. The value Ø increases with increased water activity, and at a certain aw value, it decreases with rising temperature, although this is not very notable between 25 and 30°C.
This behavior has been presented in sorption studies of water in cassava [2] and starch [12]. The value Ø represents the excess free energy at the surface, indicating an increase in the surface tension at the sorption sites, caused by the adsorbed molecules [9].
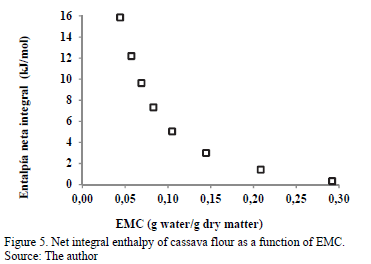
3.3.4. Net integral enthalpy of sorption
The changes in the net integral enthalpy (Qin) with equilibrium moisture content are shown in Fig. 5.
This integral was determined the same way as the differential enthalpy of sorption, but at a constant spreading pressure. The value Qin decreases with increased EMC, varying from 15.86 kJ/mol for an EMC of 0.004 g water/g d.m. to 0.334 kJ/mol for 0.2920 g water/g d.m. This thermodynamic behavior can be attributed to the saturation of the active sorption points (monolayer moisture) [9], as the water is more easily adsorbed in the active sites of the external surface of cassava flour at low moisture contents, reaching the maximum value of Qin. This maximum value is an indication of the greater water-cassava flour interaction, which means that the sorption bond sites are stronger [26]. With the increase in the equilibrium moisture, the decrease in the net integral enthalpy is evident, which is attributed to the lower favorability of the active sorption sites because they are covered with water, forming multilayers [9]. According to these results, the variation in the net integral enthalpy with EMC indicates that the level of the solid-water interaction is higher than the interaction between water molecules. According to Rizvi and Benado [36], the magnitude of the enthalpy with high moisture content reflects the presence of free water. Similar interaction between Qin and EMC has been reported in various foods, such as potato [8], potato starch [12] and macaroni [37]. The determination of integral enthalpy is useful in quantifying the energy required for drying, from an initial moisture content to a final moisture content of the food [26]. It also provides information on the microstructure of the food and the theoretical interpretation of the physical phenomena that occur at the water-food interface [38].
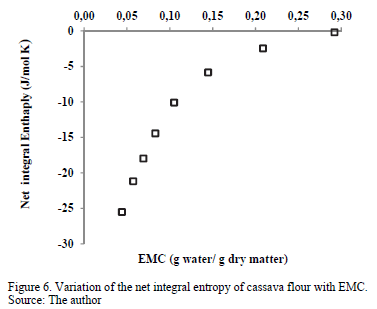
3.3.5. Net integral entropy of sorption
Fig. 6 presents the net entropy of sorption (Sin) as a function of the moisture content. All Sin values were negative, which might indicate the existence of chemical adsorption or structural modification of the adsorbent or the external surface of the solid [20]. Sin increased with increased equilibrium moisture content, varying from a minimum value of -25.50 J/mol·K for an EMC value of 0.044 g water/g d.m. to -0.1618 J/mol·K for 0.2920 g water/g d.m. This result may be associated with the greater mobility of water molecules, promoting the formation of multilayers. Thus, the net integral entropy tends to approach that of free liquid water [39]. Similar behavior was observed in the sorption of water in mango [11] and cassava [2] powder. The minimum net integral entropy value can be considered the maximum point of stability for food during storage [11]. As the water molecules are strongly bonded with the adsorbent at this zone, they are more ordered and less available to participate in deterioration reactions [40]. Therefore, this minimum Sin value is found at an EMC of 4.4% (dry matter), a value relatively close to the moisture of the monomolecular layer (xo) predicted with the GAB model (Table 1), which varied between 6.3 and 7.3% (dry matter).
4. Conclusions
The adsorption isotherms of cassava flour determined at 25, 30 and 35°C demonstrated lower water retention capacity at higher temperature. The GAB, Halsey and Peleg models are appropriate for the prediction of EMC in cassava starch between 25 and 35°C, where the Peleg model provides the best prediction. All thermodynamic properties presented a correlation with the equilibrium moisture content. The differential enthalpy, differential entropy and net integral enthalpy decreased with increased moisture. The net integral entropy increased with increased moisture, and the spreading pressure decreased with temperature and increased with aw. According to the monolayer moisture and the minimum net integral entropy value, cassava flour presents maximum stability at an EMC between 4.4 and 7.3% (dry matter). These adsorption findings in cassava flour are of interest in the determination of the optimal storage conditions, the prediction of shelf life and the optimization and quantification of energy requirements during the transfer of mass and heat during drying.
References
[1] Ayala, A., Estimación de las isotermas de adsorción y del calor isostérico en harina de yuca, Biotecnología en el Sector Agropecuario y Agroindustrial, [Online]. 9(1), pp. 88-96, 2011. Available at: http://www.scielo.org.co/pdf/bsaa/v9n1/v9n1a11.pdf [ Links ]
[2] Aviara, N. and Ajibola, O., Thermodynamics of moisture sorption in melon seed and cassava, Journal of Food Engineering, [Online]. 55(2), pp. 107-113, 2002. Available at: http://www.sciencedirect.com/science/article/pii/S0260877402000237 [ Links ]
[3] Onayemi, O. and Oluwamukomi, M., Moisture equilibria of some dehydrated Cassava and Yam Products, Journal of Food Process Engineering, 9(3), pp. 191-200, 1987. DOI: 10.1111/j.1745-4530.1987.tb00124.x [ Links ]
[4] Moreira, R., Chenlo, F., Torres, M. and Vallejo, N., Thermodynamic analysis of experimental sorption isotherms of loquat and quince fruits, Journal of Food Engineering, 88(4), pp. 514-521, 2008. DOI: 10.1016/j.jfoodeng.2008.03.011 [ Links ]
[5] Rizvi, S. and Benado, A., Thermodynamic properties of dehydrated foods, Food technology, 38(3), pp. 83-92, 1984. [ Links ]
[6] Al-Muhtaseb, A., McMinn, W. and Magee, T., Water sorption isotherms of starch powders: Part 1: Mathematical description of experimental data, Journal of Food Engineering, 61(3), pp. 297-307, 2004. DOI: 10.1016/S0260-8774(03)00133-X [ Links ]
[7] Toğrul, H. and Arslan, N., Moisture sorption behaviour and thermodynamic characteristics of rice stored in a chamber under controlled humidity, Biosystems Engineering, 95(2), pp. 181-195, 2006. DOI: 10.1016/j.biosystemseng.2006.06.011 [ Links ]
[8] McMinn, W. and Magee, T., Thermodynamic properties of moisture sorption of potato, Journal of Food Engineering, 60(2), pp. 157-165, 2003. DOI: 10.1016/S0260-8774(03)00036-0 [ Links ]
[9] Fasina, O., Ajibola, O. and Tyler, R., Thermodynamics of moisture sorption in winged bean seed and gari, Journal of Food Process Engineering, 22(6), pp. 405-418, 1999. DOI: 10.1111/j.1745-4530.1999.tb00496.x [ Links ]
[10] Mazza, G. and LeMaguer, M., Water sorption properties of yellow globe onion (Allium cepa L.), Canadian Institute of Food Science and Technology Journal, 11(4), pp. 189-193, 1978. DOI: 10.1016/S0315-5463(78)73269-4 [ Links ]
[11] Cano, D., Villa, H., Telis, J., Váquiro, H. and Nicoletti, V., Influence of alternative drying aids on water sorption of spray dried mango mix powders: A thermodynamic approach, Food and Bioproducts Processing, 93, pp. 19-28, 2015. DOI: 10.1016/j.fbp.2013.10.005 [ Links ]
[12] Al-Muhtaseb, A., McMinn, W. and Magee, T., Water sorption isotherms of starch powders. Part 2: Thermodynamic characteristics, Journal of Food Engineering, 62(2), pp. 135-142, 2004. DOI: 10.1016/S0260-8774(03)00202-4 [ Links ]
[13] Koua, B., Koffi, P., Gbaha, P., & Toure, S. Thermodynamic analysis of sorption isotherms of cassava (Manihot esculenta)., Journal of food science and technology, 51 (9), pp. 1711-23, 2014. http://dx.doi.org/10.1007/s13197-012-0687-y [ Links ]
[14] Wolf, W., Spiess, W. and Jung, G., Standardization of isotherm measurements. In: Simatos, D. and Multon, J.L. (Eds), Properties of Water in Foods. Martnus Nijhott Publishers: Dordrecht, Netherlands, 1985, pp. 661-677. [ Links ]
[15] Greenspan, L., Humidity fixed points of binary saturated aqueous solutions, Journal of Research of the National Bureau of Standards Section A: Physics and Chemistry, 81A (1), pp. 89-96, 1977. DOI: 10.6028/jres.081A.011 [ Links ]
[16] AOAC, Official methods of analysis of the Association of Oficial Analytical Chemists International. Moisture in dried fruits. Method 934.06, Arlington, USA. 1990. pp. 911-912. [ Links ]
[17] Sanni, L., Atere, C. and Kuye, A., Moisture sorption isotherms of fufu and tapioca at different temperatures, Journal of Food Engineering, 34 (2), pp. 203-212, 1997. DOI: 10.1016/S0260-8774(97)00072-1 [ Links ]
[18] Sormoli, M. and Langrish, T., Moisture sorption isotherms and net isosteric heat of sorption for spray-dried pure orange juice powder, LWT - Food Science and Technology, 62(1), pp. 875-882, 2015. DOI: 10.1016/j.lwt.2014.09.064 [ Links ]
[19] Lomauro, C., Bakshi, A. and Labuza, T., Evaluation of food moisture sorption isotherm equations Part I: Fruit, vegetable and meat products, LWT - Food Science and Technology, [Online]. 18(2), pp. 111-117, 1985. Available at: http://congtythienquang.com/data/news/Lomauro1985%20Sorption%20Isotherm%20Fruit%20Vegetable%20Meat.pdf [ Links ]
[20] Iglesias, H. and Chirife, J., A model for describing the water sorption behavior of foods, Journal of Food Science, 41(5), pp. 984-992, 1976. DOI: 10.1111/j.1365-2621.1976.tb14373.x [ Links ]
[21] Iguedjtal, T., Louka, N. and Allaf, K., Sorption isotherms of potato slices dried and texturized by controlled sudden decompression, Journal of Food Engineering, 85(2), pp. 180-190, 2008. DOI: 10.1016/j.jfoodeng.2007.06.028 [ Links ]
[22] Van den Berg, C. and Bruin S., Activity and its estimation in food systems. In: L.B. Rockland and F. Stewart. (Eds.), Water Activity: Influence on Food Quality, Academic Press, New York, 1981. pp. 147-177. [ Links ]
[23] Adebowale, A., Sanni, L., Awonorin, S., Daniel, I. and Kuye, A., Effect of cassava varieties on the sorption isotherm of tapioca grits, International Journal of Food Science & Technology, 42(4), pp. 448-452, 2007. DOI: 10.1111/j.1365-2621.2007.01261.x [ Links ]
[24] Ikhu-Omoregbe, D., Comparison of the sorption isotherm characteristics of two Cassava Products, International Journal of Food Properties, 9(2), pp. 167-177, 2006. DOI: 10.1080/10942910600592026 [ Links ]
[25] Mazza, G., Thermodynamic considerations of water vapour sorption by horseradish roots, Lebensmittel-Wissenschaft & Technologie, 13, pp. 13-17, 1980. [ Links ]
[26] Velázquez, S., Figueira, A., Rodríguez, M., Román, A., Carrillo, H. and Pérez, C., Sorption isotherms, thermodynamic properties and glass transition temperature of mucilage extracted from chia seeds (Salvia hispanica L.)., Carbohydrate Polymers, 121, pp. 411-419, 2015. DOI: 10.1016/j.carbpol.2014.11.068 [ Links ]
[27] Samapundo, S., Devlieghere, F., De Meulenaer, B., Atukwase, A., Lamboni, Y. and Debevere, J., Sorption isotherms and isosteric heats of sorption of whole yellow dent corn, Journal of Food Engineering, 79(1), pp. 168-175, 2007. DOI: 10.1016/j.jfoodeng.2006.01.040 [ Links ]
[28] Ayala-Aponte, A., Serna-Cock, L. and Rodriguez-de La Pava, G., Moisture adsorption isotherms in yellow pitahaya (Selenicereusmegalanthus), DYNA, [Online]. 78(170), pp. 7-14, 2012. Available at: http://www.scielo.org.co/scielo.php?pid=S0012-73532011000600001&script=sci_arttext [ Links ]
[29] Ciro, H., Osorio J.A. and Cortés A., Determination of the isosteric heat to plantain pulp (musa paradisiaca) by sorption isotherms, DYNA, [Online]. 75 (156), pp. 127-134, 2008. Available at: http://dyna.unalmed.edu.co/es/ediciones/156/articulos/a12v75n156/a [ Links ]
[30] Lago, C., Liendo, M. and Zapata, C., Thermodynamic sorption properties of potato and sweet potato flakes, Food and Bioproducts Processing, 91(4), pp. 389-395, 2013. DOI: 10.1016/j.fbp.2013.02.005 [ Links ]
[31] Hassini, L., Bettaieb, E., Desmorieux, H., Sandoval, S. and Touil, A., Desorption isotherms and thermodynamic properties of prickly pear seeds, Industrial Crops and Products, 67, pp. 457-465, 2015. DOI: 10.1016/j.indcrop.2015.01.078 [ Links ]
[32] Goneli, A., Corrêa, P., Oliveira, G. and Botelho, F., Water desorption and thermodynamic properties of okra seeds, American Society of Agricultural and Biological Engineers, 53(1), pp. 191-197, 2010. DOI: 10.13031/2013.29486 [ Links ]
[33] Eim, V., Rosselló, C., Femenia, A. and Simal, S., Moisture sorption isotherms and thermodynamic properties of carrot, International Journal of Food Engineering, 7(3), pp. 1-14, 2011. DOI: 10.2202/1556-3758.1804 [ Links ]
[34] Aviara, N., Ajibola, O. and Dairo, U., PH-Postharvest technology: Thermodynamics of moisture sorption in sesame seed, Biosystems Engineering, 83(4), pp. 423-431, 2002. DOI: 10.1006/bioe.2002.0124 [ Links ]
[35] Rotstein, E., The exergy balance: A diagnostic tool for energy optimization, Journal of Food Science, 48(3), pp. 945-950, 1983. DOI: 10.1111/j.1365-2621.1983.tb14936.x/pdf [ Links ]
[36] Rizvi, S. and Benado, A., Thermodynamic analysis of drying foods, Drying Technology, 2(4), pp. 471-502, 1983. DOI: abs/10.1080/07373938408959849 [ Links ]
[37] Arslan, N. and Toğrul, H., Modelling of water sorption isotherms of macaroni stored in a chamber under controlled humidity and thermodynamic approach, Journal of Food Engineering, 69(2), pp. 133-145, 2005. DOI: 10.1016/j.jfoodeng.2004.08.004 [ Links ]
[38] Rizvi, S., Thermodynamics of foods in dehydration. In: Rao, M.A., Rizvi, S.S.H. and Datta, A.K. eds., Engineering Properties of Foods, CRC Press, New York, 1986, pp. 133-214. [ Links ]
[39] Benado, A. and Rizvi, S., Thermodynamic properties of water on rice as calculated from reversible and irreversible isotherms, Journal of Food Science, [Online]. 50(1), pp. 101-105, 1985. Available at: http://onlinelibrary.wiley.com.bd.univalle.edu.co/doi/10.1111/j.1365-2621.1985.tb13286.x/epdf [ Links ]
[40] Beristain, C., Azuara, E. and Vernon, E., Effect of water activity on the stability to oxidation of spray-dried encapsulated orange peel oil using mesquite gum (Prosopis Juliflora) as wall material, Journal of Food Science, [Online]. 67(1), pp. 206-211, 2002. Available at: http://onlinelibrary.wiley.com.bd.univalle.edu.co/doi/10.1111/j.1365-2621.2002.tb11385.x/epdf [ Links ]
A.A. Ayala-Aponte, received his BSc. Eng in Agricultural Engineering in 1993 from the Universidad del Valle, Cali, Colombia and a PhD in Science and Food Technology in 2011 from the Universidad Politécnica de Valencia, España. He is a professor in the area of Food Technology and Engineering, in the Universidad del Valle, Cali, Colombia. His research interests include: preservation and food processing. ORCID: 0000-0003-0310-3577