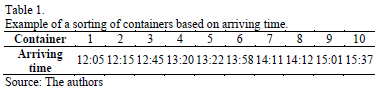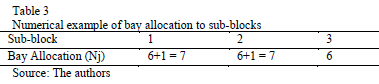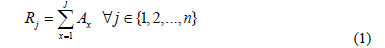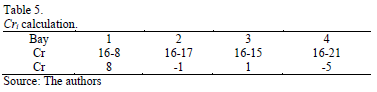Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.198 Medellín Sept. 2016
https://doi.org/10.15446/dyna.v83n198.47374
DOI: http://dx.doi.org/10.15446/dyna.v83n198.47374
An online algorithm for the container stacking problem
Un algoritmo en línea para el problema de apilamiento de contenedores
Roberto Guerra-Olivares a, Neale R. Smith a & Rosa G. González-Ramírez b
a Centro de Calidad y Manufactura, Tecnológico de Monterrey, Monterrey, México roberto.guerra@itesm.mx nsmith@itesm.mx
b Facultad de Ingeniería y Ciencias Aplicadas, Universidad de Los Andes, Santiago de Chile, Chile, rgonzalez@uandes.cl
Received: November 18th, 2014. Received in revised form: October 20th, 2015. Accepted: May 12th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Efficient cargo handling is a key element for a maritime port to compete and provide good service levels to its users. The performance of a port is related to ship-turnaround, which is conditioned by the ships loading and unloading operational efficiency. At the yard, containers are temporarily stacked in order to later either load them onto a ship or dispatch them to external users. Stacking has a strong impact on ships' service times. This paper proposes a container stacking policy, considering the particular characteristics of a container terminal in Chile. In order to measure the performance of the procedure, an upper bound for the number of re-handles of containers is estimated as a function of the block's capacity. Numerical results are provided in comparison to an upper bound, and a good performance by the proposed procedure is demonstrated.
Keywords: Container Terminal, Yard Management, Container stacking problem.
Resumen
El manejo eficiente de carga es un elemento clave para un puerto marítimo pueda competir y proveer adecuados niveles de servicio a sus usuarios. El desempeño de un puerto depende del tiempo de permanencia de la nave, que está condicionado por la eficiencia en las operaciones de carga y descarga de las naves. En el patio, los contenedores son almacenados temporalmente para ser cargados a la nave o despachados a los usuarios externos con un alto impacto en los tiempos de atención de las naves. Este artículo propone una política para stacking de contenedores, considerando las características particulares de un terminal de contenedores en Chile. Para medir el desempeño de este procedimiento, se propone una cota superior para el número de despejes de un contenedor en función de la capacidad de los bloques. Se presentan resultados numéricos en comparación con la cota superior, mostrando un buen desempeño del procedimiento propuesto.
Palabras clave: Terminal de Contenedores, Gestión del Patio, Problema de Stacking de Contenedores
1. Introduction and literature review
Containerization has lowered shipping costs and significantly increased productivity of operations related to international trade. Port terminals play a crucial role as intermodal interfaces and act as a linking node with other inland transport modes. International trade has been increasing over recent years, and with the increasing number of container shipments competition between port terminals has also increased. This means that there has been a greater demand for better service levels and value-added services to the users.
The competitiveness of a container seaport strongly relies on the service time of the ships and, hence, the minimization of the time a ship is at the berth is an overall objective with respect to terminal operations.
In order to guarantee low service times for the ships, efficient cargo handling is required, especially considering that a higher number of containers are received by the terminal due to the tendency of increasing ship sizes. The previous have motivated research and development of methods and tools to support decisions related to operations management in port terminals. Steenken et al. [1] and Stahlbock and Voß [2] provide a comprehensive survey of the state of the art of operations at container terminals as well as some models and methods that have been proposed in the literature to optimize import and export operations.
Port terminals consist of three main areas: the quay or seaside interface, the yard, and the gate or landside interface. The quay is the area where ships are berthed and quay cranes are used to transfer containers from and to the ships. There may also be some ships that have their own cranes to transfer cargo. The gate is the interface to landside, where the containers are received or dispatched to the external users by trucks, trains or barges. The yard act as a buffer for the terminal, and it is the place where containers are temporarily stored during the interval of time in which they are received and loaded on the ship (export containers), or they are unloaded from the ship and dispatched to external carriers (import containers).
The arrangement of containers within the yard clearly influences the operational continuity of the quay cranes, and hence, the operational efficiency of the port terminal. In this work we consider the problem of assigning storage space, particularly for export containers that arrive at the yard, with the aim of enhancing quay cranes productivity. In order to do this, we propose a heuristic procedure that assigns storage space to containers based on minimizing container relocation. This takes place when containers need to be moved so as a container can be reached that will be loaded onto a ship or dispatched to an external carrier.
International trade operations in Chile have shown a high level of dynamism: evidence from the current integration with world markets with a significant growth in the volume of trade over the past decade. Maritime transport is the most significant mode of transportation in Chile; more than 90% of the cargo is transferred through maritime port terminals. Chile is the economy that has the highest number of containers per capita in Latin America, and it is ranks as the 4th economy that has the highest amount of container traffic in Latin America and the Caribbean region [3]. In [4], the evolution of the port system in LAC is presented. Chile shows high level of dynamism with the emergence of secondary ports and a greater geographical spread of ports towards the south of the country.
The Port System in Chile can be classified into three main regions: northern, central, and southern. The central region of Chile contains more than 60% of the volume transferred in Chile, the ports of Valparaiso and San Antonio being the most significant in terms of TEUs. According to the port ranking provided by UN-ECLAC [5], in 2013 Chile presented a 6% positive increase of container movements in contrast to other Latin American countries that had a decreasing rate. The Port of San Antonio is positioned in 12th place in the ranking with 1,196,844 TEUs, and the Port of Valparaiso is in 16th place with 910,780 TEUs. Both ports share the same hinterland, which is comprised of the Metropolitan Region of Santiago, the Fifth and Sixth Regions of Chile, to a smaller extent from the Fourth and Seventh regions, as well as the Cuyo Region in Argentina.
The research presented in this paper is motivated by the current operations of the San Antonio International Terminal (STI for its acronym in Spanish). STI is the main terminal in the port of San Antonio, and one of the main containerized terminals in the country.
1.1. Literature review
Research into container terminal operations has attracted the attention of academics since the 1990s. Up until now, more than 6,000 articles related to container handling have been published in different international journals. The work that deals with either automated or non-automated container terminals can be distinguished in the literature, and most of the work found addresses tactical and operational planning decisions.
On a strategic decision-making level, we can find several contributions related to the location of a facility in the global supply chain network. For instance, Osorio-Ramírez et al. [6] present an evolutionary algorithm to locate container yards for a 3PL provider.
Several authors have addressed related problems in terms of yard management operations. One of the earliest works is by Kim [7], who estimated the number of moves to retrieve one container, both analytically and by simulation. Kim and Kim [8] extended previous study and incorporated yard cranes allocation decisions. Kim and Bae [9] present a model to minimize the number of export containers to be moved in the shortest possible traveling distance, considering a remarshaling strategy (containers are relocated in a dedicated space, near to the place in which the ship will be berthed). This paper does not consider a remarshaling strategy. However, the heuristic procedure proposed could be implemented for both a direct and remarshaling of containers storage space policy.
Kim and Kim [10] consider the storage space allocation problem for import containers and analyze cases with a constant, cyclic and dynamic arrival rate of import containers; the main objective is to minimize the expected number of re-handles. This work differs mainly in that we consider export containers. Kim et al. [11] use dynamic programming to determine the storage locations of export containers, grouping containers by weight. The aim of the procedure is to reduce the total number of re-handling or relocations. Previous work mainly differs in that the policy that we propose is based on a known loading sequence of containers that are to be loaded based on an estimated stowage plan.
Zhang et al. [12] formulated the storage space allocation problem (SSAP) for the Container Terminals´ storage yards. They first determine the number of containers to be placed at each block in the yard, and aim to balance the workload among blocks. They then define the number of containers associated with each vessel in terms of the total number of containers in each block and each period; the objective is to minimize the total distance traveled. The exact location of containers at the block is not defined, which is the main difference between previous research and this paper.
Bazzazi et al. [13] extend the model proposed in [12] in order to consider different types of containers. However, the authors only consider import containers, and they propose a genetic algorithm to solve the problem. Park et al. [14] present a stacking policy for incoming containers at an automated terminal. They propose an online search algorithm that dynamically adjusts and optimizes a stacking policy by generating variants of stacking policies and evaluates them while they are actually being applied, in order to determine stacking positions. The main difference with respect to this work is that we do not consider an automated terminal, and we assume that yard cranes are reach-stackers. The equipment employed at the yard significantly influences the policies that will be implemented to assign space to containers and potential container relocations.
Tapia et al. [15] present a mathematical model for the storage space allocation problem that extends upon the basic ideas proposed in [12], but goes further in considering objective functions, assigning close locations in the yard to containers that belong to the same group or segregation of containers. Ries et al. [16] propose an online algorithm to help stack of containers at the yard, based on a fuzzy logic framework. In this work, we address the same problem but we propose a heuristic algorithm in which the rules are defined based on crispy values rather than fuzzy logic rules. Another important difference in the strategy employed herein, is that we consider the current practices of the Port Terminal in which they assign storage space to containers in a two phase approach. In this approach, blocks are pre-assigned to a block, prior to the beginning of each shift, and the exact location (bay and tier) of each container is assigned in real time. Another related work is presented by Valdés-González et al. [17], which proposes a fuzzy-based strategy for the container stacking problem. It specifically considers the case study of the Port of Valparaíso in Chile. The main difference with this paper is the methodology used, which is similar to that used in [16]. Another important difference is that the Port of San Antonio and Valparaíso are very different in terms of the logistics operations; the Port of Valparaiso has a pre-terminal where all trucks are directed, and also, the port terminals have more control on the sequence of truck arrivals to their gates. A complementary problem related to the relocation of export containers incurred during the ship´s loading operations is presented by Guerra-Olivares et al. [18].
The remainder of the manuscript is organized as follows: Section 2 presents a description of the problem and practical concerns. Section 3 presents the policy description, and an estimation of an upper bound is presented in section 4. Section 5 presents numerical experiments and results. Conclusions and recommendations for future research are given in section 6.
2. Problem description and practical considerations
The container yard serves as a temporary buffer for intermodal transportation systems. The export containers must be stored in the yard for the period of time between the container drop off at the yard by external trucks and the time when the container is loaded onto the ship. Based on STI current operations, the typical time window for the stacking of export containers is around 72 hours prior to the arrival of the ship. In general, containers arrive during that time window interval in a random sequence, that is unless the terminal has implemented an appointment system, which is not the case for the STI at present.
We assume that the yard is operated by RTGs (Rubber Tyred Gantry) cranes, although in practice, only certain sectors of the yard use this handling equipment. The yard manager should decide where to allocate those containers at the yard so that a continuous flow of containers to the ship may be guaranteed in order to ensure good service times. The need for a good pre-specified space allocation policy for the containers is fundamental for the overall efficiency of the port. During the service time of a ship, it is desirable to have a continuous flow of containers between the yard and the quay.
Particularly for export operations, which are the focus of this work, it is desirable that the rate at which the containers are retrieved from the yard be equal to the rate at which the quay crane loads containers onto the vessel. If the container retrieval rate is slower, the quay crane will have idle time, and the service time of the ship will be increased. Despite the random arrivals of the containers to the port, the port has advanced knowledge of at least a preliminary version of the loading sequence of containers to the vessel. Hence, a basic assumption that we consider is that the stowage plan is a piece of input data and is already known, even if it is a preliminary version that may be updated once the ship has arrived at the terminal.
Typically, the container storage area of a port yard is constituted by blocks divided into Bays, Rows and Tiers according to the BAROTI system. A slot is defined as a BAROTI coordinate in which a TEU (Twenty-Foot Equivalent Unit) is stored. The blocks may be subdivided into sub-blocks of bays for space allocation purposes. A sub-block of bays is a set of adjacent bays. The containers are arranged based on common characteristics like destination port, weight, type, and size. A group of containers with the same characteristics is known as segregation. It is attractive to store all the containers with the same segregation in the same sub-block of bays or in consecutive ones as this may minimize the relocation or re-handling of containers during the loading operation.
The procedures to store export containers vary among port terminals. The flow of containers could be directly from the yard stack to the quay side during the loading process, or in other cases, the containers could be organized in another area (marshaling space) in which containers are sorted according to the sequence of the stowage plan. This minimizes the ship service time, but also increases the number of movements. In this work, we assume the current practice of STI in which the managers define a specific area for export containers to be stacked during the time window that has been defined prior to the arrival of the ship. There are, therefore, no pre-marshaling areas, and hence, containers are located directly to position in the yard from which they will later be retrieved to be loaded onto the ship.
3. Proposed policy description
Considering a two-stage procedure for the space assignment policy, we will focus on the online or real time assignment of space, assuming that the port manager has pre-assigned a block position for each container to be segregated in the yard. In [16], a mathematical model to support the pre-assignment of block positions to segregations is proposed. In this paper, we focus on the assignment of containers in real time to a pre-specified block, as we will further describe.
3.1. Basic policy description and notation
The policy to allocate containers within the port yard consists of a set of criteria to assign a location to each arriving export container (BAROTI coordinate). We propose a heuristic procedure based on the corresponding ship´s stowage plan. Consider the particular instance of 10 containers with their arrival times, as shown in Table 1.
The sequence in which containers will be loaded to the ship is shown in the Table 2.
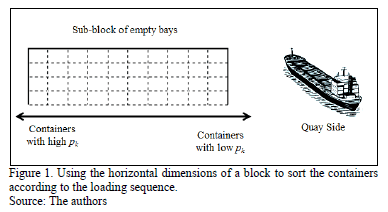
As we can observe from the Tables 1 and 2, the loading sequence of containers does not follow a FIFO (first in-first out) policy, and hence, the arrival order of containers does not define the sequence in which they are loaded. The horizontal dimension of the block can be used as an indicator of how early a specific container should be loaded to the ship, according to the stowage plan. For instance let pk be the loading sequence according to the stowage plan of the kth container to arrive at the port. Therefore, a high pk value indicates that the container will be loaded later than a container with a low pk. Fig. 1 illustrates the sub-block space allocation depending on the containers´ loading sequence).
Thus, the main principle of the proposed policy is that containers to be first loaded on to the ship, should be allocated nearer to the right hand side of the block, and the containers to be loaded later should be allocated closer to the left hand side of the block.
3.1. Algorithm description
The following notation is defined:
- Let N be the number of available bays in the block,
- Let n be the number of sub-blocks into which N bays are subdivided.
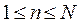 ,
, - Let Nj be the number of bays assigned to sub-block j,
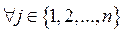 ,
, - Let A be the total number of containers to be allocated,
- Let Aj be the number of containers assigned to the sub-block j,
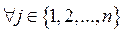 ,
, - Let ranj be the range of pk stored in sub-block j,
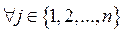 ,
, - Let sbk be the sub-block that stores container k,
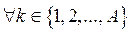 ,
, - Let ui be the number of containers stored at bay i
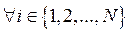 ,
, - Let Q be the maximum bay capacity, and
- Let Bj the set of opened bays in sub-block j,
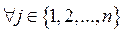 .
.
3.2.1. Parameters Estimation
Some parameters should be determined prior to the execution of the algorithm. This is described by the following subsections:
a) Minimum bay capacity to store the containers. Due to random container arrivals the position of each container k must be identified according to its position in the stowage plan, pk. Let d* be the minimum bay capacity to store A containers in the yard. Assuming that an equal number of containers is allocated to each Bay, this may be computed in the way that is shown in the following equation:
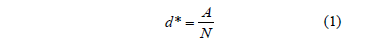
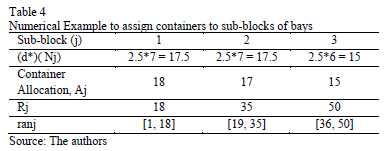
b) Number of bays that will conform each sub-block (Nj). The procedure to compute Nj is as follows: The number of sub-blocks (n) is an input parameter, so [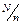 ]bays are allocated to each sub-block. To complete allocating all the bays of each sub-block, one extra bay should be allocated to the first mod(N, n) bays. For example, with N = 20 bays and n = 3 sub-blocks, each of the 3 sub-blocks will contain 6 bays. Since mod(20, 3) = 2, sub-blocks 1 and 2 will each be assigned one extra bay. The final bay allocation to each sub-block is shown in Table 3. The sub-blocks are sorted according to their proximity to quay. In this example, sub-block number 1 is the closest to the quay while sub-block number 3 is the farthest from the quay.
]bays are allocated to each sub-block. To complete allocating all the bays of each sub-block, one extra bay should be allocated to the first mod(N, n) bays. For example, with N = 20 bays and n = 3 sub-blocks, each of the 3 sub-blocks will contain 6 bays. Since mod(20, 3) = 2, sub-blocks 1 and 2 will each be assigned one extra bay. The final bay allocation to each sub-block is shown in Table 3. The sub-blocks are sorted according to their proximity to quay. In this example, sub-block number 1 is the closest to the quay while sub-block number 3 is the farthest from the quay.
c) Number of containers to be allocated to sub-block j (Aj ). For each sub-block j, the product of the minimum bay capacity and the number of bays assigned to the sub-block j gives the number of containers assigned to each sub-block, 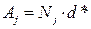 . If this value is not an integer, it should be adjusted based on the following considerations:
. If this value is not an integer, it should be adjusted based on the following considerations:
- For the sub-blocks with the minimum the value of Aj will be equal to
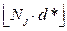 .
. - For the sub-blocks with the maximum Nj, the value of Aj will be equal to
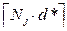 .
.
Additional adjustment of Aj may be required if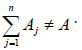 . When the total number of containers assigned to all n sub-blocks is greater than A, the Aj for the sub-block with the maximum container allocation should decrease by
. When the total number of containers assigned to all n sub-blocks is greater than A, the Aj for the sub-block with the maximum container allocation should decrease by 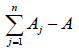 units.
units.
- Equivalently, when the total number of containers assigned to all n sub-blocks is less than A, the Aj for the sub-block with the minimum container allocation should increase by
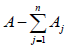 units.
units.
Once Aj is defined, parameter ranj can be determined as follows:
- Let Rj be the accumulate value of Aj:
- Sub-blocks with j = 1 store the containers with pk in the range ran1= [1, R1].
- Sub-blocks with j = {2, 3, , n} store containers with pk in the range ranj = [Rj-1 + 1, Rj]
In order to illustrate previous procedure, consider the case with a value of A = 50 containers, N = 20 Bays, d* = 2.5 and n = 3 sub-blocks. After applying the previous steps, the final container allocation of each sub-block is presented in the Table 4.
3.4. Heuristic description
A heuristic procedure is designed to assign containers to bays. The block of bays is subdivided into n sub-blocks and instances; different values of n were generated to examine the dependence of the number of re-handles with this parameter. The heuristic proceeds to fill the bays by allocating containers from the left to the right of the sub-block and from the back to the front of the sub-block. The algorithm assumes that the sub-blocks of bays are empty at the beginning and that each sub-block is filled up with containers according to ranj. When a new container arrives it is allocated either in an opened sub-block bay or in a new empty sub-block bay. The containers are allocated so that the number of re-handles required to load them onto the ship are minimized.
The parameters that define an instance of the problem are the number of sub-blocks in which the block of bays will be subdivided (n), and the maximum tolerable difference between loading sequences in the stowage plan (Crmax). Thus, one instance consists of the following parameters:
- Number of containers, A.
- Number of bays, N.
- Number of sub-blocks, n.
- Maximum capacity of the bay, Q.
- Maximum tolerable difference Crmax.
Suppose the first container to arrive at the port yard has pk = p1 and is allocated in the upper left corner of the corresponding sub-block. Due to random arrivals, suppose that the second has pk = p2 with p2 < p1; so the second container could be located in front of the first. To retrieve both containers will not necessarily involve any re-handle movement. However, all the containers having pk between p2 and p1 should be located somewhere else, and the total delayed time to load all the containers onto the ship will increase due to crane displacement to different sectors of the sub-block. To avoid the previous situation we estimate the difference between the last container allocated in each opened bay of the sub-block j and the container waiting to be allocated as shown in the following equation:

Where:
- pik-1 is the loading sequence of the last container allocated to bay i,
- pk is the loading sequence of the arriving container, and,
- Bj is the set of all opened bays in sub-block j.
A Cri difference should be computed between the loading sequence of the incoming container and the loading sequence of the last container assigned to each opened bay in the sub-block. We are interested only in negative values of Cri because they indicate that no re-handles will be required if the incoming container is allocated in bay i. The value of Cri is restricted to a maximum tolerable value, defined as Crmax. If the value of Cri is greater to or equal than Crmax, the container can be located in bay i.
The methodology can be summarized by the following series of steps:
1. Sort the containers according to their arrival order
.
2. Match the containers with the stowage plan and determine pk..
3. Determine sbk
by matching with ranj..
4. Initialize
.
5. Initialize ui = 0
.
6. Set k = 1.
7. If sbk is empty, open the first bay of sbkand go to step 8, otherwise go to step 9.
8. Allocate the container in the bay opened in step 7 and add the bay to Bsbk, then go to step 17.
9. Calculate cri
.
10. Determine the maximum negative element of cri. If no element of cri is negative go to step 12.
11. If the cri obtained in step 10 is greater or equal than Crmax, allocate the container in the bay i and go to step 17. If not, proceed to step 12.
12. If possible, open a new bay in the sub-block and add the bay to Bsbk. If all bays of the sub-block are already opened, go to step 14.
13. Allocate the container in the block opened in step 12, and then go to step 17.
14. Calculate cri
for any container with arrival order m, with
,and sbm = sbk.
15. Reserve bay i when a negative value of cri is found.
16. Allocate the container k in the emptiest and unreserved bay of sbk.
17. Set k = k + 1 and ui = ui +1.
18. If ui = Q, remove the bay i from Bsbk.
19. If
go to step 7, otherwise go to step 20.
20. End of the algorithm.
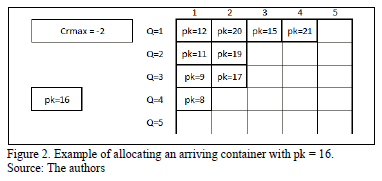
To illustrate the methodology, we provide a numerical example. Figure 2 shows a graphical representation of a block of 5 bays, each one has a maximum capacity of 5 containers. The bay number 5 has not yet been opened. There are 9 containers already in the block, and the tenth container to arrive to the port has a pk = 16. Cri values for bays 1, 2, 3 and 4 should be calculated in order to determine in which bays the incoming container can be assigned.
The value of Cr for the bay 1 is calculated as follows: Cr1 = 16 - 8 = 8. Table 5 shows the Cri differences of all opened bays. Some Cri differences are positive and others are negative. A Cri greater than 0, such as the Cr of bay numbers 1 and 3, indicates that if the container with pk = 16 is allocated in any of those a re-handle movement will be required to retrieve the container.
According to the algorithm, the bays that are allowed to receive a container are those with a negative Cri value. Table 5 shows the Cri values for all opened bays. In this example, bays 2 and 5 are possible candidates to receive the container. The Crmax is equal to -2, so bays with a value of Cr= -1 or Cr = -2 can be chosen. The algorithm will compare the Cri value of all candidates with the Crmax, and the final decision will be to allocate the container in bay number 2.
As can be observed in Table 5, a value of Cr = -1 implies that the containers have consecutive values of pk, and in general, a negative value indicates that no re-handles are required to retrieve the pair of containers. The decision to open a new bay must be taken only when all the Cri differences are positive or there is no longer a negative Cr greater or equal than Crmax for all opened bays in the block.
To open or use a new bay there must be at least one empty bay in the sub-block. When a container arrives, but it is not possible to open a new bay due to all bays being opened in the sub-block, the following methodology is performed:
- Inspect if there is any Cri < 0 for any container that has not yet arrived from the sub-block.
- When a Cri < 0 is found, reserve the bay for that container.
- Allocate the newcomer container in the emptiest and a bay that is not reserved in the sub-block.
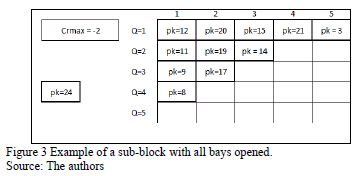
Fig. 3 shows a numerical example of this situation. For the container with pk = 24, the Cri vector is: {16, 7, 10, 3, 21}. Neither component of the vector is negative, so the algorithm will verify if there is a negative Cri for any not container that has not arrived.
4. Upper bound estimation
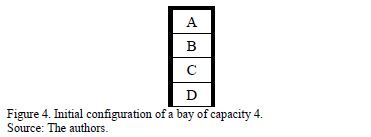
In this section we present an estimation of an upper bound on the maximum and an expected number of re-handles of a bay with capacity Q. In order to estimate the number of re-handles, we assume that containers are retrieved by a reach-stacker crane. The reach stacker crane can retrieve containers only from the front side of the stack, and the maximum stack height reached by the equipment is five. We assume that all the containers that need to be moved to retrieve the container are relocated in the same configuration as they were previously stacked in the block. Consider a bay with a capacity of 4 containers, as is illustrated in Figure 4.
Suppose that the sequence to retrieve the containers according to the stowage plan is {A, B, C, D}. Three re-handles (D, C, B) are required to retrieve container A. Once container A was retrieved, two additional re-handles are required to retrieve container B. Then, one additional re-handle should be made to retrieve container C. The last container to be retrieved does not require re-handles, so the total re-handles required to retrieve all the containers are: 3+2+1 = 6. This configuration is the worst one possible due to the order of retrieving the containers being exactly the opposite of the order of the containers allocated in the bay.
Let Max_Rhand be the upper bound in the number of re-handles of a Bay with capacity Q. The maximum number of re-handles of a bay with capacity Q provides an upper bound (the worst case) for the number of re-handles that may be used to evaluate the effectiveness of the algorithm, which is expressed in the following equation:
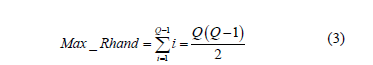
We may also use for comparison purposes the expected value of the number of re-handles for a bay with capacity Q. To define this value we compute the distribution of the number of interferences and the number of permutations. For example, the same bay in the previous example with capacity 4 has 4! = 24 possible permutations. The minimum number of re-handles that can be obtained is 0 when the order of retrieving the containers is exactly the same as the order of the containers allocated in the bay. By generating the 24 permutations and the number of re-handles in each permutation, the corresponding distribution obtained is that shown in Table 6.
Assuming an equal occurrence probability for each permutation, the expected value of the number of re-handles can be obtained by the weighted average as follows:
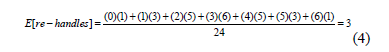
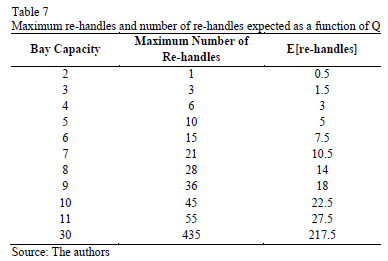
The previous procedure was applied to different values of the capacity of a bay in order to obtain the corresponding value of the maximum and expected number of re-handles, as shown in Table 7.
A polynomial trend line was fitted to the data, and we obtained the following expression to determine the expected number of re-handles:
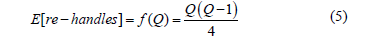
5. Numerical results and experimentation
5.1. Instance generation
We consider three types of instance sizes, according to the relationship between the number of containers and the total available slots to allocate the containers: Tight, Medium and Relaxed. We defined the values of the capacity of each bay as the product of the number of rows and tiers. Typical values based on the case study of STI are 6 and 5 respectively, which corresponds to a value of Q = 30. These are also the values considered for the instances generated. The number of sub-blocks could be any integer in the range of (1, N), where the extreme cases are represented by the values of 1 and N when n = 1. The entire block is treated as the unique sub-block in the instance while if n = N each single bay of the block is treated as a sub-block.
We define a range of values for each parameter that will later be described. Based on the historical data of the port terminal under consideration we assume that, on average, 90 trucks per hour arrive at the port terminal during the first and second shift in the day. We will consider therefore, that for a congested operational day, there is a maximum arrival of 1500 trucks. For an uncongested day, we will consider that 800 trucks arrive: thus, AÎ{800, 1500}. The rest of the parameters are defined as: NÎ {tight, medium, relaxed}; n Î{1, 3, 20, N}; QÎ {30} and Crmax Î {2, 4}.
By considering previous values for each parameter we generate a total of 2x3x4x2=48 types of instances. The values of N corresponding to tight, relaxed, and medium ranges are estimated as follows:

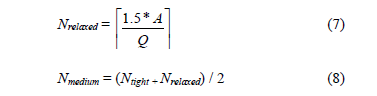
5.2. Numerical experiments
The numerical experimentation was performed on an Intel Core i5 Computer with 2.50 GHz and 6.0 GB of RAM. The maximum number of re-handles in a bay with a capacity of 30 containers is defined as:
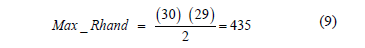
While the expected value of Re-handles is defined as:
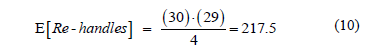
Considering the solution provided by the algorithm, we determined the number of re-handles per bay (R_bay) and compared this number to the upper bound that can be defined as the expected number of re-handles, as shown in the following equation:
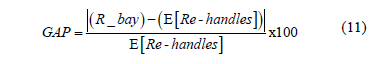
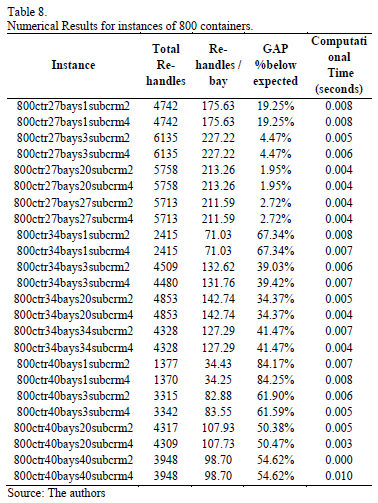
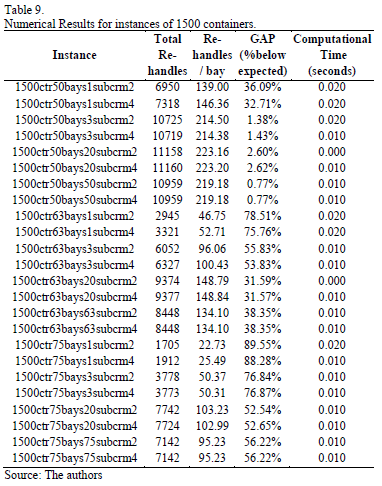
The value of the gap obtained may be interpreted as the percentage below the expected value of Re-handles. The bigger the gap, the better the algorithm performs. Tables 8 and 9 show the results for the 800 size and 1500 size instances respectively. We consider a single replicate for the 48 types of instances, which are refereed based on the values of its parameters. For example, the "800ctr27bays1subcrm2" is an instance with 800 containers, 27 bays, 1 sub-block and Crmax = 2. The tables present the total number of re-handles obtained by the solution, the number of re-handles per bay and the corresponding gaps and computation times. Gaps are expressed as a percentage value below the expected number of re-handles.
As can be observed in the tables, all instances found a number of re-handles that were less than the expected number of re-handles that was estimated as an upper bound. As we previously defined, positive gaps indicate a better performance of the heuristic procedure. From the above tables, the 800 size instances obtained an average gap of 38.48% and the 1500 size instances an average gap of 42.97%. This indicates that for both instance sizes the heuristic performs on average similar. Also, there are no big differences with respect to the size of the instance in terms of the number of containers is observed.
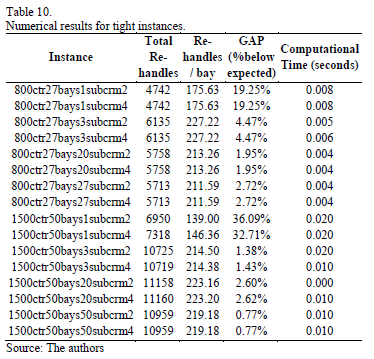
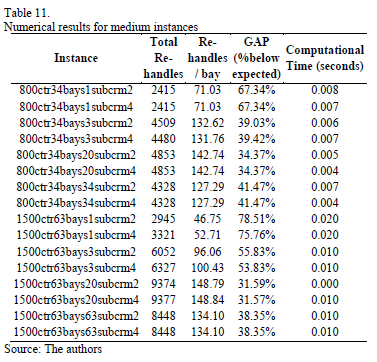
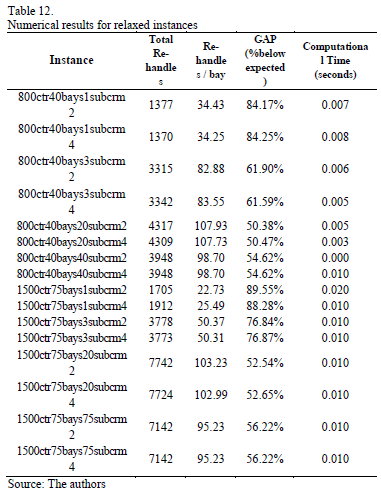
Moreover, for both sizes of containers, we observe that gaps increase proportionally as the instances are less restricted. Also, the best results are obtained when all the block of bays are treated as a single sub-block, e.g. with n = 1. Execution time for all the instances is less than 0.1 second, which is a very short computational time due to the polynomial characteristics of the algorithm that is proposed. Smaller computational times are observed for the 800 size instances, but even for the 1500 size these are quite small and adequate for an online procedure. Tables 10, 11 and 12 present results that are summarized by the type of instance: tight, medium, and relaxed, respectively.
As we can observe from previous tables, tight instances present the lower gaps, with an average gap of 8.45%, and a maximum gap of 36%, which shows that are the hardest instances to be solved and the number of re-handles is closer to the expected number computed as an upper bound. It is important to notice that for this type of instance, better results are obtained for the 1500 size instances than for the 800 size.
In the case of the 800 tight instances, no difference on the results obtained for different values of Crmax are observed. On the other hand, the relaxed instances show the best results (higher gaps), with an average value of 65%. Medium instances have an average gap of 48%, which is an intermediate value with respect to the relaxed and tight instances.
6. Conclusions and recommendations for further research
We have proposed a heuristic procedure for the allocation of storage space for export containers arriving at a Port Terminal. We specifically consider the case in which the terminal defines a specific area in which export containers are stacked during the time window that is fixed prior to the arrival of the ship. Containers that arrive with more anticipation are allocated to other spaces from which they are relocated to the stacking area during the time window period.
The aim of the procedure is to minimize the number of potential re-handles of containers once they are retrieved from the yard to be loaded onto the ship. The heuristic consists of a set of criteria to assign a location in a space within the yard based on the sequence in which the container will be loaded to the ship, and as is indicated in the stowage plan. We present computational results with a set of different sized instances and the restrictiveness that were generated.
An upper bound on the number of expected re-handles of containers as a function of the capacity of a bay was determined in order to measure the performance of the heuristic procedure. Results show that the heuristic always finds lower values of the number of re-handles with respect to the upper bound. The instances that turned out to be more difficult are the tight type in which the gap with respect to the upper bound is not as high as for the rest of the instances. Computation times are very small with lower values of 0.1 seconds.
For further research, we propose that the algorithm to the import containers that are unloaded from the ship in extended in order to minimize the number of re-handles when they are dispatched to external trucks. We also consider an extension of the procedure in which the number of sub-blocks of bays (n) may be determined instead of considering it as a parameter to be another area of future research.
References
[1] Steenken, D., Voß, S. and Stahlbock, R., Container terminal operations and operations research-A classification and literature review. OR Spectrum vol. 26, pp. 3-49, 2004. DOI 10.1007/s00291-003-0157-z. [ Links ]
[2] Stahlbock, R., and Voß, S., Operations research at container terminals: A literature update. OR Spectrum, 30, pp. 1-52, 2008. DOI 10.1007/s00291-007-0100-9. [ Links ]
[3] Rodriguez, J.-P., The benefits of logistics investments: Opportunities for Latin America and the Caribbean. Technical notes, Inter-American Development Bank, 2012. IDB-TN-395. [ Links ]
[4] Wilsmeier, G., Monios, J. and Pérez-Salas, G., Port system evolution in Latin America and the Caribbean. Journal of Transport Geography, 39, pp. 208-221, 2014. DOI: 10.1016/j.jtrangeo.2014.07.007 [ Links ]
[5] Doerr, O., Latin American and the Caribbean Container port throughput, Ranking 2013. Infrastructure Services Unit |NRID| ECLAC | United Nations, 2013 [ Links ]
[6] Osorio-Ramírez, C., Arango-Serna, M.D., Adarme-Jaimes, W., Implementing an evolutionary algorithm for locating container yards of a 3PL provider. DYNA, 81(187), pp. 49-55, 2014. DOI: 10.15446/dyna.v81n187.40044. [ Links ]
[7] Kim, K.H., Evaluation of the number of re-handles in container yards. Computers and Industrial Engineering, 32(4), pp. 701-711, 1997. DOI 10.1016/S0360-8352(97)00024-7. [ Links ]
[8] Kim, K.H. and Kim, H.B., The optimal determination of the space requirement and the number of transfer cranes for import containers. Computers and Industrial Engineering, 35(3-4), pp. 427-430, 1998. DOI: 10.1016/S0360-8352(98)00125-9. [ Links ]
[9] Kim, K.H. ans Bae, J.W., Re-marshaling export containers in port container terminals. Computers and Industrial Engineering, 35(3-4), pp. 655-658, 1998. DOI: 10.1016/S0360-8352(98)00182-X. [ Links ]
[10] Kim, K.H. and Kim, H.B., Segregating space allocation models for container inventories in port container terminals. International Journal of Production Economics, 59, pp. 415-423, 1999. DOI: 10.1016/S0925-5273(98)00028-0 [ Links ]
[11] Kim, K.H., Park, Y.M. and Ryu, K.-R., Deriving decision rules to locate export containers in container yards, European Journal of Operational Research, 124, pp. 89-101, 2000. DOI: 10.1016/S0377-2217(99)00116-2 [ Links ]
[12] Zhang, C., Wan, Y.-W., Liu, J. and Linn, J.R., Dynamic crane deployment in container storage yards, Transportation Research Part B, 36, pp. 537-555, 2003. DOI: 10.1016/S0191-2615(01)00017-0 [ Links ]
[13] Bazzazi, M., Safaei, N. and Javadian, N., A genetic algorithm to solve the storage space allocation problem in a container terminal. Computers & Industrial Engineering, 56, pp. 44-52, 2009. DOI: 10.1016/j.cie.2008.03.012 [ Links ]
[14] Park, T., Choe, R., Kim, Y. H. and Ryu, K.R., Dynamic adjustment of container stacking policy in an automated container terminal, International Journal of Production Economics, 133, pp. 385-392, 2011. DOI: 10.1016/j.ijpe.2010.03.024 [ Links ]
[15] Tapia, F., Covarrubias, R., Miranda, P. and González-Ramírez R.G., On the storage space allocation problem. Proceedings of 22nd International Conference on Production Research (ICPR), Brazil, 2013. [ Links ]
[16] Ries, J., González-Ramírez, R.G. and Miranda, P., A fuzzy logic model for the container stacking problem at the container terminal. Lecture Notes in Computers Sciences, LNCS 8760, pp. 93-111, 2014. DOI: 10.1007/978-3-319-11421-7_7 [ Links ]
[17] Valdés-González, H., Reyes-Bozo, L., Vyhmeister, E., Salazar, J.L., Sepúlveda, P.E. and Mosca-Arestizábal, M., Container stacking revenue management system: A fuzzy-based strategy for Valparaiso port. DYNA 82(190), pp. 38-45. DOI: 10.15446/dyna.v82n190.42311 [ Links ]
[18] Guerra-Olivares, R., González-Ramírez, R.G. and Smith, N., A heuristic procedure for the outbound container relocation problem during export loading operations. Mathematical Problems in Engineering, Article ID 201749, 2015, 13 P. DOI: 10.1155/2015/201749 [ Links ]
R. Guerra-Olivares, is an Operations Analyst at Madisa-Cat in Monterrey, Mexico. He holds a Ph.D in Engineering Science from the Tecnológico de Monterrey, Monterrey Campus in Mexico. He holds a BSc. in Chemical Engineering from the Tecnológico de Monterrey and a MSc. in Energy Engineering from the same university. He also holds a MSc. degree in Industrial Engineering from the Pontificia Universidad Católica de Valparaíso, Chile. He has one book published in LAP LAMBERT Academic Publishing GmBH & Co. KG and several papers in proceedings of national and international seminars. ORCID: orcid.org/0000-0001-6929-800X.
N.R. Smith, is an associate professor at the Quality and Manufacturing Center at the Tecnológico de Monterey, Campus Monterrey in Mexico where he currently directs the Doctoral Program in Engineering Science. He holds a BSc. in Industrial Engineering from the University of Arizona and MSc. and PhD degrees in Industrial Engineering from Georgia Tech. He has taught both undergraduate and graduate level courses in operations research, logistics and supply chain management. His research interests are in the areas of operations research and logistics and he has advised and co-advised both Master's and PhD theses. He has published in journals such as the International Journal of Production Research and the European Journal of Operational Research, among others. Before pursuing an academic career, he was a consultant and implemented logistics-related solutions for numerous companies. ORCID: orcid.org/0000-0002-1477-8388
R.G. González-Ramírez, is a professor and researcher in the Faculty of Engineering and Applied Sciences at the Universidad de Los Andes, Chile. She holds a BSc. in Industrial Engineering from the Technologic Institute of Morelia, a MSc. in Industrial Engineering from Arizona State University, a MSc. in Quality and Productivity Systems and a PhD. in Engineering Sciences from the Tecnológico de Monterrey in Mexico. Her research includes port logistics and intermodal transport of cargo, supply chain management, trade facilitation and optimization techniques. She has been working in applied research projects and is currently an active researcher in the Program Digital and Collaborative Network of Ports in Latin America and the Caribbean leaded by the Economic System of Latin America and the Caribbean, SELA and the Latin America Development Bank CAF. ORCID: orcid.org/0000-0001-8029-5432.