Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.198 Medellín set. 2016
https://doi.org/10.15446/dyna.v83n198.51310
DOI: http://dx.doi.org/10.15446/dyna.v83n198.51310
Multi-product inventory modeling with demand forecasting and Bayesian optimization
Modelo de inventario multi-producto, con pronósticos de demanda y optimización Bayesiana
Marisol Valencia-Cárdenas a, Francisco Javier Díaz-Serna b & Juan Carlos Correa-Morales c
a Institución Universitaria Tecnológico de Antioquia, Medellín, Colombia. mvalencia@unal.edu.co
b Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. javidiaz@unal.edu.co
c Facultad de Ciencias, Universidad Nacional de Colombia, Medellín, Colombia. jccorrea@unal.edu.co
Received: June 16th, 2015. Received in revised form: November 1st, 2015. Accepted: July 25th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The complexity of supply chains requires advanced methods to schedule companies' inventories. This paper presents a comparison of model forecasts of demand for multiple products, choosing the best among the following: autoregressive integrated moving average (ARIMA), exponential smoothing (ES), a Bayesian regression model (BRM), and a Bayesian dynamic linear model (BDLM). To this end, cases in which the time series is normally distributed are first simulated. Second, sales predictions for three products of a gas service station are estimated using the four models, revealing the BRM to be the best model. Subsequently, the multi-product inventory model is optimized. To define the policies for ordering, inventory, costs, and profits, a Bayesian search integrating elements of a Tabu search is used to improve the solution. This inventory model optimization process is then applied to the case of a gas service station in Colombia.
Keywords: Dynamic Linear Models, Inventory Models, Forecasts, Bayesian Statistics.
Resumen
La complejidad de las cadenas de suministro exige mejores métodos para programar los inventarios de una empresa. En este trabajo se presenta una comparación entre modelos de pronósticos de demanda de múltiples productos, eligiendo el mejor entre: ARIMA, Suavización exponencial, Regresión Lineal Bayesiana y un Modelo Lineal Dinámico Bayesiano. Para ello, primero se realiza una simulación de casos donde no hay una Distribución Normal en las series de tiempo, segundo, se estiman las predicciones de ventas de tres productos de una estación de servicios de gasolina con los cuatro modelos, encontrando los mejores resultados para la Regresión Lineal Bayesiana. Seguido a esto, se presenta la optimización de un Modelo de Inventarios Multi-Producto. Para definir la política de pedidos, inventarios, costos y ganancias, se utiliza una búsqueda bayesiana, que integra elementos de búsqueda Tabú para mejorar la solución. Dicha Optimización del Modelo de Inventarios se aplica a un caso de una estación de combustibles en Colombia.
Palabras clave: Modelos Dinámicos Lineales, Modelos de Inventarios, Pronósticos, Estadística Bayesiana.
1. Introduction
The increasing complexity of supply chains resulting from the globalization of market economies, changes in customer preferences, and increasing competition among companies is intensifying the search for faster and better methods for decision-making and obtaining optimal solutions for several types of inventory systems.
In inventory models, as noted by Simchi-Levi [1,2], demand represents a very important variable that warrants substantial attention to determine adequate inventory policies, and in some cases, the behavior of this variable is stochastic, generating the need for accurate forecasting methods. However, problems can arise because on occasion, the forecasting models are inappropriate or mistakes are made, leading to error-laden inventory policies.
Other problems associated with forecasting demand are related to changes in the distribution function, which produce a lack of stability in the time series [3]; indeed, " a time series is unstable if there are frequent and significant changes in the distribution" [3]. This phenomenon has been cited by different authors [4-6]. Other disadvantages are that, sometimes, the models of interest cannot satisfy some theoretical assumptions, such as normality in residuals or constant variance. Alternatively, the researcher may not have sufficient required data for model estimation.
In this sense, Bayesian statistics can be very good alternative for making inferences using different types of models [7-9], as shown for Bayesian forecasting with the Holt winters model [10], the dynamic models proposed in [8,11], and especially, the situation described in [12], in which the authors describe making forecasts in R using a package they developed. Other works report using a combination of Bayesian techniques for forecasting [13-15], and [14] reveals that using such combinations results in increased accuracy and reliability. Bayesian forecasting has many practical applications [8,10,11,16-31]. These methods constitute alternatives to forecast and can be compared with classical methods to identify ways to further increase the accuracy of the required predictions.
In addition to the analytical techniques that can be used to solve inventory models, a practical problem-solving approach exists that is known as heuristics. Heuristics can be programmed according to some rules, but obtaining the optimal solution for a model is not always guaranteed.
Some works relating to inventory models have applied heuristic optimization. The Tabu Search algorithm can be used to search for solutions to inventory problems; for example, according to [32], this algorithm was used to minimize the inventory costs of an organization's final products and gave a better result than the company policy. Indeed, when it was applied to a real situation involving the same products with the same time horizon, it reduced inventory costs by 20% while achieving a 100% service level. In [33], the Tabu Search algorithm is applied to determine the optimum level of orders. Genetic algorithms can be used for efficient supply chain management [34] in multi-product scenarios, but such scenarios are infrequently analyzed using inventory models. A recent work in Colombia [35] proposed a model of multi-product inventory between companies to minimize logistics costs in an urban distribution operational context. In all of these cases, demand was predicted. The measure symmetric mean absolute percentage error (SMAPE), as described in [36], is useful when the response takes values close to zero because using it does not cause the error percentage to increase more when a response is very small.
In their book Dynamic Linear Models with R, Petris et al. [12] demonstrate many applications and the use of the package dlm, which they developed. They also list the error indicators used to compare models: mean absolute percentage error (MAPE), mean absolute deviation (MAD) and mean squared error (MSE) or root-mean-square error (RMSE).
In this paper, first, we report a simulation study allowing the recreation and analysis of the behavior of a demand time series with dynamic variation after finding an adequate model to forecast these types of data. The compared models are as follows: autoregressive integrated moving average (ARIMA); exponential smoothing (ES), a novel model developed in a doctoral thesis [37]; a Bayesian regression model (BRM); and a modified Bayesian dynamic linear model (BDLM) presented in that thesis in which a MAPE indicator is used for the comparisons. In this paper, the estimated models are compared using the SMAPE for forecasts once the data have been partitioned. Then, after applying the best model to a real case of combustible demand for a Colombian gas service station, the prediction is saved to do an optimization process.
Finally, we propose a multi-product inventory model that provides not only orders, inventory values, costs, and profits but also transportation durations and costs. The solutions obtained by this optimization process are based on a search that utilizes a Bayesian form to predict orders based on the previous forecasted demands. However, unlike that described in the aforementioned thesis, here, no missing values are considered, and the result for 15 days of planning is shown.
2. Demand forecasting
We consider four models for making predictions: ARIMA, ES, BRM, and BDLM. For this purpose, we program an algorithm using R software to choose the best possible forecast.
The ARIMA(p,d,q) model, which was developed in 1970, by George Box and Gwilym Jenkins [38,39] has been widely studied [40-44]. This model incorporates the characteristics of the same time series according to the autocorrelation results and makes predictions based on historical data.
ES is another oft-used technique [10,45,46] that employs exponential weights of past periods' values in the same series. This model can incorporate the level of the time series, trend and seasonality and it is expressed as follows: 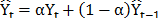 , where
, where 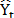 is the forecast for the next period, a is the smoothing constant,
is the forecast for the next period, a is the smoothing constant, 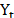 is the real value of the series in period t, and
is the real value of the series in period t, and 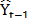 is the predicted value for the period t-1. The response variable
is the predicted value for the period t-1. The response variable 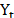 is adjusted according to a time horizon, and the sum of squared errors of prediction (SSE) value is optimized by searching for the value of a that minimizes it.
is adjusted according to a time horizon, and the sum of squared errors of prediction (SSE) value is optimized by searching for the value of a that minimizes it.
Bayesian statistics relies on different assumptions than classical models. For example, the parameters of a probability distribution are random variables, q, and prior quantitative information is included in a probability distribution [47,48] known as 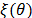 , with simple information (y1, y2,
, yn) summarized by the likelihood function L(y1, y2,
, yn | q). Using the Bayes theorem-the a prior distribution
, with simple information (y1, y2,
, yn) summarized by the likelihood function L(y1, y2,
, yn | q). Using the Bayes theorem-the a prior distribution 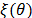 multiplied by the likelihood-gives the posterior distribution
multiplied by the likelihood-gives the posterior distribution 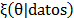 . The predictive distribution is the integral of the distribution of the variable to be forecasted and the posterior distribution [49,50].
. The predictive distribution is the integral of the distribution of the variable to be forecasted and the posterior distribution [49,50].
2.1. Bayesian regression model (BRM)
In [51], Zellner presents a BRM based on a diffuse prior distribution of b parameters. In this work, a different model will be presented: the novel BRM described in thesis above [37]. The model presented there assumes a Normal prior distribution for the vector parameter b and applies an iterative process to the initial vector b0 for every time t; however, its accuracy parameter is fixed: t0 = 1/s., The predictive distribution used for forecasting is derived in the thesis and is a Student's t-distribution; this derivation is also presented in the appendix of this paper.
The general equation of a linear model is the same in a Bayesian regression, but the estimation process is different. We describe this process here based on the general equation given by eq. (1), where yt is the demand vector, and x1, , xk are the explanatory variables.
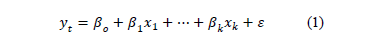
The likelihood function of the data, based in the Normal distribution, is shown in eq. (2), a prior Normal distribution for the b parameter vector, in eq. (3) and the posterior distribution is (4), obtained after the product of the prior times the likelihood, and the algebraic process. Here, 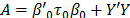 , and
, and 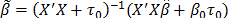
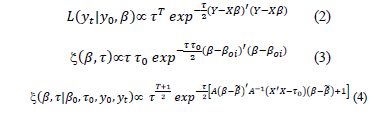
After taking the integral of the product of the posterior and future data distributions, the resulting predictive distribution is described by eq. (5), which is a Student's t-distribution, with mean 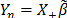 , n degrees of freedom, and variance according to eq. (6). The forecasting process uses the eq. (5), and its mean considers the designed matrix X based on the adjustment of the regression eq. (1). The analytical formulation of this predictive distribution is also explained in the appendix.
, n degrees of freedom, and variance according to eq. (6). The forecasting process uses the eq. (5), and its mean considers the designed matrix X based on the adjustment of the regression eq. (1). The analytical formulation of this predictive distribution is also explained in the appendix.
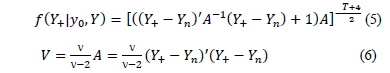
2.2. Bayesian dynamic linear model (BDLM)
In [21], Meinhold and Singpurwalla explain the process used to update 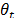 in a recursive form using the posterior Normal distribution to update the observed equation. The model proposed in this work is based on the procedure described in the aforementioned thesis [37], except that the mean value of the posterior Normal distribution are modified based on an average of past values before estimating the observation equation and without the M model used by Meinhold and Singpurwalla. The process is included in the algorithm designed in the R program.
in a recursive form using the posterior Normal distribution to update the observed equation. The model proposed in this work is based on the procedure described in the aforementioned thesis [37], except that the mean value of the posterior Normal distribution are modified based on an average of past values before estimating the observation equation and without the M model used by Meinhold and Singpurwalla. The process is included in the algorithm designed in the R program.
2.3. Simulation of the forecasting process
We simulate different time series under control conditions. For the simulated series, an estimation process is executed using classical and Bayesian techniques. Subsequently, a comparison is conducted using the SMAPE indicator. The objective is to determine the best forecasting model to use if the time series exhibits high variability and apply it to a real case to obtain predicted values useful for developing and proposing an inventory policy.
The demands analyzed are mainly of a continuous nature, but they do not always follow a Normal distribution. The following cases are used to create the simulated time series:
S1. Regression model with skew Normal distribution for errors, with seasonal and dynamic variation.
S2. Regression model with skew T-distribution for errors, with seasonal and dynamic variation.
S3. Random variable with Poisson distribution.
S4. Random variable with Poisson distribution and seasonal and dynamic variation.
The size of each time series is N = 63 data points and a seasonal variation of seven periods. Each time series consists of 49 data points for the adjustment and 14 data points for forecasting.
The SMAPE of the forecasted values is used as the criterion for identifying the best model, and it is calculated with eq. (7) according to [36], after estimating each of the four models being compared: ARIMA, ES, BRM, and BDLM.
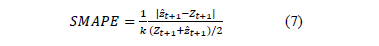
where:
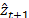 : Forecasted value of the demand at period t+1.
: Forecasted value of the demand at period t+1.
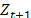 : Real value of the demand at period t+1.
: Real value of the demand at period t+1.
N : Total number of data points.
k : Total number of forecasted data points.
N-k : Total number of data points used to adjust the model.
The algorithms for the simulation were developed using the R program [52]. For the BRM, a vector of 200 percentile values is calculated, and then, a prediction is made using the Student-t predictive distribution. The error indicator SMAPE is calculated for the adjusted and forecasted data for all models to facilitate finding the minimum SMAPE value.
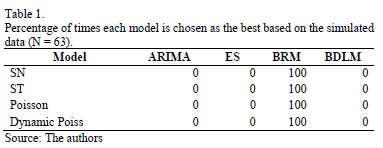
This process is repeated a thousand times, and the program calculates the percentage of selection for every model and simulated case. The results of the frequency with which each tested model is chosen as the best model are shown in Table 1. For all simulated time series, the BRM is identified as the best model.
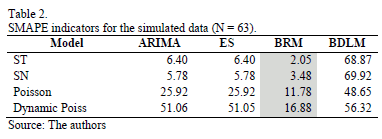
Table 2 shows that, for one simulated case, as indicated by the grey color, lower SMAPE values are found for the BRM in all analyzed cases. The results of the two tables are consistent for all scenarios, confirming the reliability of the results.
These results show that when few data points with high variance are used, the BRM model produces the minimum SMAPE values for all simulated series.
Up to this point, we have shown that in forecasting, when no Normal behavior exists, the BRM is a very good alternative, to the two common used classical models and the new BDLM model, which failed to provide good results in any case.
3. Multi-product inventory modeling
3.1. Previous models
Some classical inventory models were formulated based on Wagner and Whitin's proposed[53] cost minimization. These authors specify that an order could be '0' or the sum of some demands, and they formulated schemes for ordering (i.e., choosing between generating orders or not) in every period t.
The model formulated by Wagner and Whitin, which is cited in [54], assumes that a sequence of orders over a planning horizon with a duration of T exists. The model assumptions are shown in Table 3.
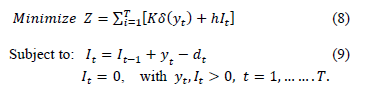
where the eq. (9) describes the inventory-balance constraint for every period t.
3.2. Proposed multi-product inventory model
A general mathematical model of inventory management is formulated, and subsequently, an optimization algorithm is developed.
We propose performing profit maximization using a formula similar to the Wagner-Within model with the addition of transportation costs CTRt. Almost equivalent results can be obtained by considering the problem as one of cost minimization.
Objective function for the inventory model.
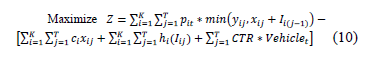
Subject to an inventory balance constraint
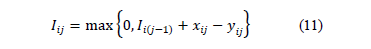
Capacity constrains for the orders

The number of vehicles
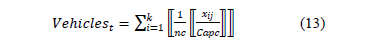
where 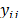 represents the forecasted demand for product i in period j. The transportation quantities and their respective costs will depend on the number of vehicles to be used (Vehiclest), which depend on the number of compartments, nc, and these, depend on those compartments' capacities, Capc, assuming equal values. Dividing the quantity to order xij into Capc, generates a number of compartments, and the maximum integer value of this number is divided into nc, producing the total number of vehicles required, as represented by eq. (13), which can then be substituted into the objective function shown in eq. (10).
represents the forecasted demand for product i in period j. The transportation quantities and their respective costs will depend on the number of vehicles to be used (Vehiclest), which depend on the number of compartments, nc, and these, depend on those compartments' capacities, Capc, assuming equal values. Dividing the quantity to order xij into Capc, generates a number of compartments, and the maximum integer value of this number is divided into nc, producing the total number of vehicles required, as represented by eq. (13), which can then be substituted into the objective function shown in eq. (10).
The final inventory 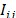 can be 0 or positive, depending on the orders placed, as described in this work. The inventories are limited by the storage capacity. Therefore, the orders cannot exceed that capacity and can be equal to that maximum when there is zero inventory
can be 0 or positive, depending on the orders placed, as described in this work. The inventories are limited by the storage capacity. Therefore, the orders cannot exceed that capacity and can be equal to that maximum when there is zero inventory
3.1.1. Algorithm
We describe the scenarios analyzed to solve the proposed multi-product inventory model. The algorithm was programmed in R software.
The schemes to order are of two kinds, S1 and S2, and the model was explained in the past section. These schemes are replaced in the same model of the equations (10) to (13), and the best solution is kept, in order to be compared and finding the maximum possible profits. The process is repeated, and the random variable S, added to the orders (see Table 5), helps to find a best possible solution, after a period prepared to simulate.
Two types of schemes are used for ordering: S1 and S2; the model is described above. These schemes are substituted into the model described by eqs. (10)-(13), and the best solution is retained for posterior comparison and profit maximization with the results obtained after the process repetition, by using the random variable S, which is added to the orders (Table 5), and it facilitates finding the best possible solution for the simulated period.
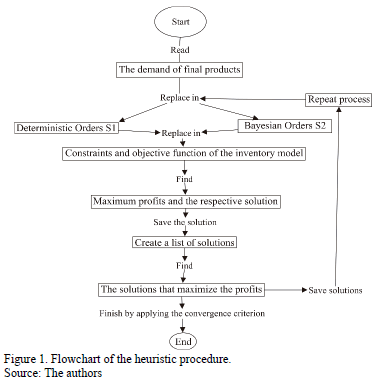
We calculate a maximum solution for each S1-model and S2-model combination and save the best of them. After performing a simulation of size "sim", a list of solutions is created, and subsequently, the saved maximums are compared, the higher value is selected, and the process is repeated until the best possible solution is obtained according to the following convergence criterion: a difference of zero between ten consecutive values of Z.
This process is presented in Fig. 1.
• Ordering schemes
The first ordering scheme, S1, is based on theorem 2 of [53], which states that "there exists an optimal program such that for all t":
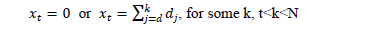
Thus, the formulation of S1 considers the dynamics shown in Table 5. These R vectors of values are replaced in the model described by eqs. (10)-(13), saving all of the equations and the objective function, and finding the solution that maximizes the profits.
The second scheme, S2, generates orders based on a predictive Bayesian distribution, as explained in section 3.2.2. This allows a random variable based on the Bayesian process that depends on previously forecasted demands to update the posterior distribution. Subsequently, scheme S1 is used with random order values.
Ordering schemes: Explanations corresponding to Table 5:
1. Ordering in the first period to satisfy all the demands estimated for the planning horizon.
2. Ordering in the first period to satisfy only demand 1, and ordering in the second period to satisfy the sum of the remaining demands.
3. Ordering in the first two periods, and ordering in the third period to satisfy the sum of the remaining demands.
4. Same as 2 and 3 for resting periods, until T-1; no ordering in the T-th period.
5. Ordering every two periods.
6. Ordering every three periods.
7. Ordering every four periods and so on.
8. Ordering the economic order quantity (EOQ).
M. Ordering in all periods.
3.1.2. Bayesian optimization
This is the procedure involving the second scheme proposed (S2). The assumptions of this process are as follows:
The data distribution is uniform (Data-unif(a1,b1)). Let 'm' be the mean value of this distribution, with a prior Normal truncated distribution with the following parameters: µo, mean; so, standard deviation (assumed to be constant); a, inferior limit; and b: superior limit (10).
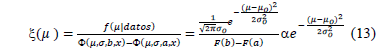
The product of the prior distribution and the likelihood function is the Truncated Normal (TN), that is, the posterior distribution (eq. (14)) of the mean parameters of the final predictive distribution.
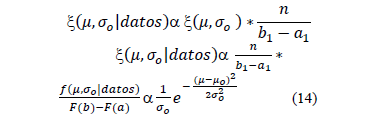
The predictive distribution is the integral of the Uniform distribution of the data and the posterior TN (14). This distribution is uniform (15) and is used for forecasting, after updating the means, with the posterior distribution for every time t.
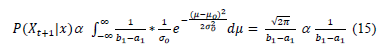
4. Results
4.1. Comparison of the forecast results obtained using a real case
The dataset of the fuel sales includes 92 daily values for each product: Regular, Extra, and Diesel. In total, 77 data points will be used to adjust the models, and 15 data points will be used for forecasting. The last forecasted values will be used to optimize the models. For the BRM, a vector of 200 percentiles was used to identify the best possible position of the predictive Student T-distribution based on the minimum SMAPE value of the 15 forecasts.
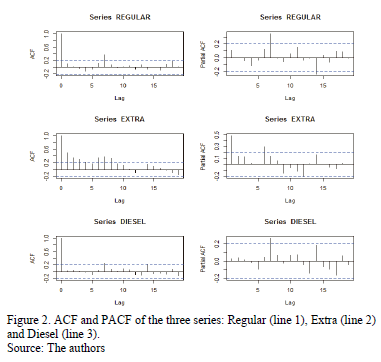
In the description of the Regular and Diesel combustibles, the behavior seems to have a seasonal pattern with seventh-order dependence, whereas for Extra, the behavior of the autocorrelation shows a dependence of first order (Fig. 2), and it also shows seasonality every 7 periods (days). These aspects are considered to estimate the models and are used to define covariables to represent these behaviors.
We also found that the residuals of the ARIMA models estimated do not follow the normality assumption.
• Description of the time series analysis
Fig. 2 presents the autocorrelation and partial autocorrelation functions (ACF and PACF, respectively), they show that the time series exhibits dependence of different orders (i.e., Regular, Extra and Diesel fuels).
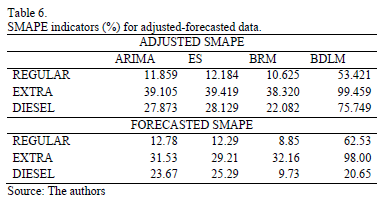
Table 6 presents the adjusted and forecasted SMAPE indicators (adjusted-forecasted), when the criterion used to make a choice is based on one of these. Some advantages of the BRM models are clearly evident.
According to the adjustment criteria, the BRM is the best at forecasting the three products. Additionally, among the forecasted values, the BRM produces the best results for Regular and Diesel fuels, whereas for Extra, the ES is better, followed by ARIMA (it should be noted that ARIMA's result is close to that of the BRM). The minimum adjustment criterion is important because a researcher interested in forecasting would not be able to choose the future data. Indeed, when the BRM is selected, the probability of obtaining good performance is high. This approach leads us choose the BRM as the model to forecast to these time series.
The results obtained by applying the optimization process to a 15-day time horizon of fuel distribution and inventory planning are presented below.
4.2. Optimization of the application of the inventory model to a real case
If there were no holding costs and if the inventory capacity were very high, the optimum strategy would be to send all the demand for the T periods on the first day.
However, based on the real cost and capacity data, the results obtained depend on the state of the initial inventories. The designed algorithm compares the four combination models proposed and requires no more than 1 minute to produce results when the initial inventories exceed zero:
- When the initial inventories are set according to real data (4300, 1000, and 2150 gallons of Regular, Extra, and Diesel, respectively), the maximum profit is $69,432.115, and the orders are not sent every day. Instead, Regular fuel orders are sent on days 4, 7, 8, 10, 11 and 13, and Extra fuel orders are sent on days 7, 10 and 13. The model did not indicate that sending diesel fuel was necessary because of the initial inventory.
- When the initial inventories are all equal to zero, the optimal profit is $12,737.930. However, companies typically prefer to have non-zero initial inventories.
4.3. Validation
- Using real data, the profits were $30,334.447 for a 15-day planning period.
- Using the model proposed here, with current initial inventories for each fuel (4300, 1000, and 2150 gallons of Regular, Extra, and Diesel fuel, respectively) and by substituting the planned orders for the real sales, the profits are $53,619.824, which is higher than the original value. This difference represents a saving of 58.7% relative to the current situation ($30,334.447).
This result shows that the model can provide a better solution for inventory management than what was achieved in the real case.
5. Discussion
The proposed Bayesian forecasting methods establish various accurate alternatives for making predictions compared to some classical methods, such as ARIMA and ES. The modified version of the BRM proposed in the aforementioned thesis [37] (in this case, the SMAPE indicator is used) was capable of generating satisfactory results, as was also shown using MAPE in the thesis.
This alternative Bayesian method can be improved by altering its parameters or probability distributions to obtain more accurate values, which would result in a better optimization solution. Additionally, different research lines could potentially benefit from this optimization technique, which can also be applied to the Dynamic Linear Models described by other authors, including Petris, Harrison and Stevens, and Harrison and West [8,9,11].
6. Conclusions
In addition to maximizing its profits, the proposed inventory model could also consider the fuel transportation costs incurred by the gas service station, and it functions a very good planning tool, especially compared to other models, such as EOQ, which was not found to be the best model in any case. Transportation costs change in every period, and it is not necessary to send vehicles every day. This model also revealed that sending all of the 15-day demands at the beginning of each period was non-optimal, since these quantities involved could exceed the available storage capacities. Furthermore, the model indicated that, if the related costs were zero and the capacity were very high, satisfying all the demands of the T periods during the first period would be optimal.
Appendix
Here, we show the transformation of the exponent in eq. (4) to obtain the predictive Student T-distribution (5).
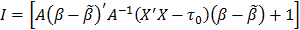
Where 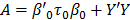 , and
, and 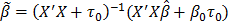 . The exponent can also be expressed as:
. The exponent can also be expressed as:
I = Y'+Y+-b'n M bn +Y'Y +b "0t0b0
Where M-1 = (X'+X+ + X'X + t0)-1, and bn = M-1(X'Y + X'+Y + b0t0)
I = Y'+Y+- M-1(X'Y + X'+Y+ + b0t0)M M-1(X'Y + X"+Y+ + b0t0) + Y'Y + b'0t0b0
I = Y'+Y+ + Y'Y + b'0t0b0 - M-1[(X"Y)"(X"Y)
+ (X"+Y+)"(X"+Y+) + (b0t0)"b0t0 + 2(X'Y)'(X'+Y+) +
2(X"Y)"(b0t0) + 2(X'+Y+)"(b0t0)]
I = Y+(I-X+M-1X+)Y+ - 2Y+X+M-1(X"Y + b0t0) + b"0t0b0 - M-1(Y X"X"Y + t0b'0 b0t0 + 2X"Y b0t0) + Y'Y
I = [Y+Y+- 2Y+X+(I - M-1X"+X+)-1M-1(X"Y + b0t0)]*
(1 - M-1X"+X"+) + (b'0t0b0 - M-1t0b'0 b0t0) + (Y'(I - M-1X"X)Y - 2M-1X"Y b0t0)
I = [(Y+- Yn)"(Y+- Yn) - Yn"Yn](1 - M-1X"+X"+) +
(b'0t0b0 - M-1t0b'0b0t0)
+ (Y"Y - 2M-1(I - M-1X"X)-1X"Y b0t0)(I - M-1X"X)
I = [(Y+- Yn)"(Y+- Yn) - Yn"Yn](1 - M-1X"+X"+) +
(b'0t0b0 - M-1t0b'0 b0t0)
+ [(Y - Ym)"(Y - Ym) - Y'mYm] (I - M-1X"X)
Where Yn = (I - X+M-1X+)-1X+M-1(X"Y + b0t0), according to a definition of inverted difference in matrices [51].
Yn = (I + X+(X"X)-1X+)M-1X + (X"Y + b0t0)
Therefore, Yn = (I + (X'X)-1X'+X+)(X"X + t + X"+X+)-1X+(X"Y + b0t0)
= (I + (X"X)-1X'+X+)(I + (X"X+ t0)-1X'+X+)-1X+ (X'X + t0)-1(X"Y + b0t0)
t0 is a very small quantity. Thus, Yn = (X"X + t0)-1X+(X"Y + b0t0) = 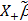 , and
, and
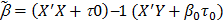 . Let Ym = M-1(I - M-1X'X ) -1X'b0t0
. Let Ym = M-1(I - M-1X'X ) -1X'b0t0
Some terms disappear because of the proportionality:
I = [(Y+- Yn)'(Y+- Yn) - Yn'Yn](1 - M-1X'+X+) + [(Y - Ym)"(Y - Ym) - YmYm](I - M-1X"X)
I = [(Y+- Yn)'(Y+- Yn) + (Y - Ym)'(Y - Ym)
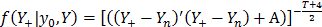
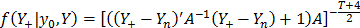
which is the Student t-distribution described by eq. (5).
Acknowledgments
Colciencias is acknowledged for providing a scholarship (567) in support of obtaining a Doctorate in Engineering-Industry and Organizations at Universidad Nacional de Colombia, Sede Medellín.
References
[1] Simchi-Levi, D., Kaminski, P. and Simchi-Levi, E., Designing and managing the supply chain. 3rd ed. New York: McGraw-Hill; 2008. [ Links ]
[2] Chen, X. and Simchi-Levi, D., Coordinating inventory control and pricing strategies with random demand and fixed ordering cost: The finite horizon case. Operations Research, 2004, 52(6), pp. 887-896. DOI: 10.1287/opre.1040.0127 [ Links ]
[3] Hillier, F. y Hillier, M., Métodos cuantitativos para administración. Third Ed. City: México. McGraw-Hill; 2007. [ Links ]
[4] Garcia, C.A., Ibeas, A., Vilanova, R. and Herrera, J., Inventory control of supply chains: Mitigating the bullwhip effect by centralized and decentralized internal model control approaches. European Journal of Operational Research, 224(2), pp. 261-272, 2013. DOI: 10.1016/J.EJOR.2012.07.029 [ Links ]
[5] Sarimveis, H., Patrinos, P., Tarantilis, C.D. and Kiranoudis, C.T., Dynamic modeling and control of supply chain systems: A review. Computers and Operations Research. 35(11), pp. 3530-3561, 2008. DOI: 10.1016/J.COR.2007.01.017 [ Links ]
[6] Braun, M.W., Rivera, D.E., Flores, M.E., Carlyle, W.M. and Kempf, K.G., A model predictive control framework for robust management of multi-product, multi-echelon demand networks. Annual Reviews in Control, 27(2), pp. 229-245, 2003. DOI: 10.1016/j.arcontrol.2003.09.006 [ Links ]
[7] Pole, A., West, M. and Harrison, J., Nonnormal and nonlinear dynamic Bayesian modeling. In Bayesian analysis of time series and dynamic linear models. New York: Marcel Dekker; 1988, pp. 167-198. [ Links ]
[8] West, M. and Harrison, J., Bayesian forecasting and dynamic models. Second ed. New York: Springer Series in Statistics; 1997. [ Links ]
[9] Petris, G., An R package for dynamic linear models. Journal of Statistical Software [online], 36(12), pp. 1-16, 2010. Available at: http://www.jstatsoft.org/ [ Links ]
[10] Bermúdez, J.D., Segura, J.V. and Vercher, E., Bayesian forecasting with the Holt-Winters model. Journal of the Operational Research Society, 61(1), pp. 164-171, 2009. DOI: 10.1057/jors.2008.152. [ Links ]
[11] Harrison, J. and Stevens, C., Bayesian forecasting. Journal of the Royan Statistical Society, 38(3), pp. 205-247, 1976. [ Links ]
[12] Petris, G., Petrone, S. and Campagnoli, P., Dynamic linear models with R [online]. 2009. Available at: http://www.springer.com/statistics/statistical+theory+and+methods/book/978-0-387-77237-0 [ Links ]
[13] Kociecki, A., Kolasa, M. and Rubaszek, M., A Bayesian method of combining judgmental and model-based density forecasts. Economic Modelling, 29, pp. 1349-1355, 2012. DOI: 10.1016/j.econmod.2012.03.004 [ Links ]
[14] Coelho, C., Pezzulli, S, Balmaseda, M., Doblas-Reyes, F. and Stephenson, D., Forecast calibration and combination: A simple Bayesian approach for ENSO. Journal of Climate. 17(7), pp. 1504-1516, 2004. DOI: DOI: 10.1175/1520-0442(2004)017<1504:FCACAS>2.0.CO;2 [ Links ]
[15] Andersson, M. and Karlson, S., Bayesian forecast combination for VAR models. Sveriges Riskbanc-working Papers [online]. pp. 1-17, 2007. Available at: http://www.riksbank.se/Upload/Dokument_riksbank/Kat_publicerat/WorkingPapers/2007/wp216.pdf [ Links ]
[16] Bijak, J., Bayesian methods in international migration forecasting. CEFMR Working Papers. Warsaw: Central European Forum for Migration Research, 2005. [ Links ]
[17] Clements, M.P. and Hendry, D.F.H., Forecasting non-stationary economic time series. Cambridge: MIT Press; 2000, pp. 1-6. [ Links ]
[18] Craig, P., Goldstein, M., Rougier, J. and Seheult, A.H., Bayesian forecasting for complex systems using computer simulators. Journal of the American Statistical Association, 96(454), pp. 717-729, 2001. [ Links ]
[19] Duncan, G., Gorr, W. and Szczypula, J., Bayesian unrelated time forecasting series: For seemingly to local forecasting application government revenue. Management Science, 39(3), pp. 275-293, 1993. [ Links ]
[20] Li, G., Shi, J. and Zhou, J., Bayesian adaptive combination of short-term wind speed forecasts from neural network models. Renewable Energy, 36(1), pp. 352-359, 2011. DOI: 10.1016/j.renene.2010.06.049 [ Links ]
[21] Meinhold, R.J. and Singpurwalla, N.D., Understanding the Kalman Filter. The American Statistician, 37(2), pp. 123-127, 1983. DOI: 10.2307/2685871 [ Links ]
[22] Neelamegham, R. and Chintagunta, P., A Bayesian model to forecast new product performance in domestic and international markets. Marketing Science [online]. 18(2), pp. 115-136, 1999. Available at: http://bear.warrington.ufl.edu/centers/mks/articles/684541.pdf [ Links ]
[23] Oracle, Inc., The Bayesian Approach to Forecasting [online], 2006. Available at: http://www.oracle.com/us/products/applications/057028.pdf [ Links ]
[24] Pedroza, C., A Bayesian forecasting model: Predicting U.S. male mortality. Biostatistics, 7(4), pp. 530-550, 2006. [ Links ]
[25] Pezzulli, S., Frederic, P., Majithia, S., Sabbagh, S, Black, E, Sutton, R, et al., The seasonal forecast of electricity demand: A simple Bayesian model with climatological weather generator. Applied Stochastic Models in Business and Industry, 22(2), pp. 1-16, 2006. Available at: http://empslocal.ex.ac.uk/people/staff/dbs202/publications/2005/pezzullib.pdf [ Links ]
[26] Popova, I., Popova, E. and George, E., Bayesian forecasting of prepayment rates for individual pools of mortgages. Bayesian Analysis, 3(2), pp. 393-426, 2008. [ Links ]
[27] Putnam, B., Practical experiences in financial markets using Bayesian forecasting systems [online], 2007. Available at: http://www.math.uchicago.edu/~cfm/BP-papers/Lessons_from_Bayesian_Experiences.pdf [ Links ]
[28] Sloughter, J.M., Raftery, A.E. and Gneiting, T., Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Monthly Weather Review, 135(9), pp. 3208-3220, 2006. [ Links ]
[29] Valencia, M., and Correa, J. Un modelo dinámico bayesiano para pronóstico de energía diaria. Revista Ingenieria Industrial. 2013;12(2), pp.7-17. [ Links ]
[30] Valencia, M., Correa J.C., Díaz F. y Ramírez, S., Aplicación de modelación bayesiana y optimización para pronósticos de demanda. Ingenería y Desarrollo, 32(2), pp. 179-199, 2014. [ Links ]
[31] Yelland, P.M., Bayesian forecasting of parts demand. International Journal of Forecasting, 26(2), pp. 374-396, 2010. DOI: 10.1016/j.ijforecast.2009.11.001 [ Links ]
[32] Valencia, M., González, D. y Cardona, J., Metodología de un modelo de optimización para el pronóstico y manejo de inventarios usando el metaheurístico Tabu. Revista de Ingeniería. 24(1), pp. 13-27, 2014. DOI: 10.15517/ring.v24i1.13771 [ Links ]
[33] Urrea, A. y Torres, F., Optimización de una política de inventarios por medio de búsqueda tabú. In: III Congreso colombiano y I Conferencia Andina internacional [online], 8 P. 2006, Available at: http://dspace.uniandes.edu.co:9090/xmlui/handle/1992/822 [ Links ]
[34] Jeyanthi, N. and Radhakrishnan, P., Optimizing multi product inventory using genetic algorithm for efficient supply chain management involving lead time. International Journal of Computer Science and Network Security [online], 10(5), pp. 231-239, 2010. Available at: http://paper.ijcsns.org/07_book/201005/20100534.pdf [ Links ]
[35] Palacio, O. y Adarme, W., Coordinación de inventarios: Un caso de estudio para la logística de ciudad. DYNA, 81(186), pp. 295-303, 2014. [ Links ]
[36] Wallström, P. and Segerstedt, A., Evaluation of forecasting error measurements and techniques for intermittent demand. International Journal of Production Economics, 128(2), pp. 625-636, 2010. [ Links ]
[37] Valencia, M., Dynamic model for the multiproduct inventory optimization with multivariate.PhD. Thesis. Department of Engineering, Facultad de Minas, Universidad Nacional de Colombia, Sede Medellín, Colombia, 2016. [ Links ]
[38] Bowerman, B.L. y Oconnell, R.T., Pronósticos, series de tiempo y regresión: Un enfoque aplicado. Editores. CL, editor. México, 2007. [ Links ]
[39] Valencia, M., Ramírez, S., Tabares, J. y Velásquez, C., Métodos de pronósticos clásicos y bayesianos con aplicaciones. Report. Universidad Nacional de Colombia, 2014. [ Links ]
[40] Wei, W.W.S., Time series analysis. Reading: Addison-Wesley, 1994. [ Links ]
[41] Makridakis, S., Hibon, M. and Moser, C., Accuracy of forecasting: An empirical Investigation. Journal of the Royal Statistical Society. Series A, 142(2), pp. 97-145, 1979. DOI: 10.2307/2345077. [ Links ]
[42] Makridakis, S., Wheelwright, S. and McGee, V., City: NewYork. Second Ed. John Wiley and Sons, 1983. [ Links ]
[43] Diebold, F., Elementos de pronósticos. City: México. International Thomson editors, 1999. [ Links ]
[44] Wilson, J.H., Keating, B. and Galt, J., Pronósticos en los negocios. Fifth Ed. McGraw-Hill; 2007. 461 P. [ Links ]
[45] Wang, S., Exponential smoothing for forecasting and bayesian validation of computer models [online]. Thesis, Georgia Institute of Technology, [Online]. 2006. Available at: https://smartech.gatech.edu/bitstream/handle/1853/19753/wang_shuchun_200612_phd.pdf [ Links ]
[46] Yelland, P.M. and Lee, E., Forecasting product sales with dynamic linear mixture models. Sun Microsystems, 2003. [ Links ]
[47] Gill, J., Bayesian methods: A social and behavioral sciences approach. Second Ed. Boca Raton: Chapman and Hall, 2007. [ Links ]
[48] Gelman, A., Carlin, J.B., Stern, H.S. and Rubin, D.B., Bayesian data analysis. Second Ed. Boca Raton: Chapman and Hall, 2004. [ Links ]
[49] Barrera, C. y Correa, J., Distribución predictiva bayesiana para modelos de pruebas de vida vía MCMC. Revista Colombiana de Estadística [online], 31(2), pp. 145-155, 2008. Available at: http://www.emis.ams.org/journals/RCE/ingles/V31/bodyv31n2/v31n2a01BarreraCorrea.pdf [ Links ]
[50] Congdon, P., Bayesian statistical modelling. London: Wiley Series in Probability and Statistics, 2002. [ Links ]
[51] Zellner, A., An introduction to bayesian inference in econometrics. Second Ed. New York: Wiley, 1996. [ Links ]
[52] R Core Team., A Language and environment for statistical computing [online]. Vienna: R Foundation for Statistical Computing, 2014. Available at: http://www.r-project.org/ [ Links ]
[53] Wagner, H.M. and Whitin, T.M., Dynamic version of the economic lot size model. Management Science, 5(1), pp. 89-96, 1958. [ Links ]
[54] Simchi-Levi, D., Chen, X. and Bramel, J., The logic of logistics: Theory, algorithms, and applications for logistics and supply chain management. Second Ed. New York: Springer-Verlag, 2005. [ Links ]
M. Valencia-Cárdenas, es Ing. Industrial en 2000, Esp. en Estadística, en 2002, MSc. en Ciencias-Estadística, en 2010. PhD en Ingeniería, Industria y Organizaciones, de la Universidad Nacional de Colombia, Sede Medellín. Ha trabajado en aplicaciones estadísticas, estadística industrial, optimización. Actualmente docente de la Institución Universitaria Tecnológico de Antioquia, Medellín, Colombia. Áreas de interés: métodos estadísticos, optimización con aplicaciones a la industria. ORCID:orcid.org/0000-0003-3135-3012
F.J. Díaz-Serna, es Ing. Industrial en 1982, Esp. en Gestión para el Desarrollo Empresarial en 2001, MSc. en Ingeniería de Sistemas en 1993, PhD en Ingeniería en 2011. Áreas de trabajo: ingeniería industrial, administrativa y de sistemas. Actualmente, profesor asociado del Departamento de Ciencias de la Computación y la Decisión, Facultad de Minas, Universidad Nacional de Colombia, Sede Medellín, Colombia. Áreas de interés: investigación de operaciones, optimización, sistemas energéticos, producción, dinámica de sistemas. ORCID:orcid.org/0000-0003-1057-1862
J.C. Correa-Morales, es Estadístico en 1980, MSc. en Estadística en 1989, PhD en Estadística en 1993. Áreas de trabajo: estadística, bio estadística, estadística industrial. Profesor asociado de la Escuela de Estadística, Universidad Nacional de Colombia, Sede Medellín, Colombia. Áreas de interés: análisis multivariado de datos, bioestadística, estadística bayesiana. ORCID: orcid.org/0000-0002-9368-4725