Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.199 Medellín dez. 2016
https://doi.org/10.15446/dyna.v83n199.55945
DOI: http://dx.doi.org/10.15446/dyna.v83n199.55945
Procedure to energetic analysis of centrifugal pumping systems
Procedimiento para el análisis energético de sistemas de bombeo centrífugos
Manoel Socorro Santos-Azevedo a, Carlos A. de León-Benítez b, Jandecy Cabral-Leite a & Ignacio Pérez-Abril b
a Instituto de Tecnología Galileo del Amazonas, Manaus, Brasil. manoelazevedo@yahoo.com.br, jandecycabral@hotmail.com
b Universidad Central Marta Abreu de Las Villas, Cuba. charle@uclv.edu.cu, iperez@uclv.edu.cu
Received: February 29th, de 2016. Received in revised form: August 8th, 2016. Accepted: September 29th, 2016
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
The renewed interest in the efficient use of energy, has made the use of speed control by frequency variation for flow control in pumping systems, has now become the most attractive option for this purpose, the which makes it necessary to obtain as accurately as possible energy saving in comparison with other mechanical means used for this purpose. This paper presents a mathematical procedure that reduces the limitations of application of laws affinity on systems with high initial static load for calculation of potential savings when employed these drives is developed.
Keywords: Affinity law, centrifugal pumps, energy saving.
Resumen
El renovado interés por el uso eficiente de la energía, ha hecho que el empleo del control de velocidad por variación de frecuencia para la regulación del flujo en sistemas de bombeo, se haya convertido en la actualidad en la opción más atractiva con este fin, lo cual hace que sea preciso obtener con la mayor precisión posible el ahorro de energía en comparación con otros medios mecánicos utilizados con este objetivo. En este trabajo se desarrolla un procedimiento matemático que permite reducir las limitaciones de aplicación de las leyes de afinidad en sistemas con elevada carga estática inicial, para el cálculo de los potenciales de ahorro cuando son empleados estos accionamientos.
Palabras clave: Leyes de afinidad, bombas centrifugas, ahorro de energía.
1. Introducción
Hoy en día, aproximadamente 22% de la energía suministrada a los motores eléctricos es consumida por los sistemas de bombeo [1-3]. Debido al renovado interés en el ahorro de energía, el empleo de accionamientos eléctricos de frecuencia variable (AEFV), se ha convertido en la mejor opción para su empleo en tales sistemas lo que se traduce en un importante ahorro energético en comparación con medios mecánicos para ajustar el flujo en dichos sistemas [3-5] Hay un gran número de tipos de bombas que se utilizan en aplicaciones industriales, las más difundidas son las bombas centrifugas
La aplicación de las leyes de afinidad en bombas centrífugas debe hacerse con cautela [6]. Generalmente, pueden ser aplicadas cuando el sistema de bombeo tiene una alta carga de fricción en comparación con la carga estática. Esto es debido a que las leyes de afinidad son más precisas cuando se aplican entre las curvas de rendimiento que están a una misma eficiencia de la bomba [1] Las leyes de afinidad consideran que la disminución de la velocidad no afecta la eficiencia de la bomba. Esta aproximación puede ser considerada como válida hasta una reducción de velocidad igual a 0.7 veces la velocidad nominal [7] Sin embargo la eficiencia en el nuevo punto de operación debe ser chequeada en todos los casos, especialmente en sistemas con alta carga estática [8-10]. No tener en cuenta; lo anteriormente planteado introduce una incertidumbre en los cálculos de los potenciales de ahorro de energía en las diferentes variantes de control de flujo en los sistemas de bombeo. El procedimiento desarrollado en este trabajo permite disminuir la incertidumbre en el cálculo de los potenciales de ahorro de energía cuando se analiza la factibilidad de empleo de los variadores de velocidad en estas aplicaciones.
2. Materiales y métodos
2.1. Leyes de afinidad
Las leyes de afinidad gobiernan las relaciones entre velocidad, presión de descarga y potencia de entrada de la bomba y permiten predecir el rendimiento de una bomba a una velocidad que no sea la característica.
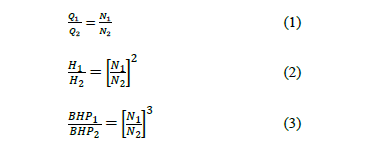
Donde:
Q: Flujo volumétrico (m3/hr.)
N: Velocidad de la bomba (rpm)
H: Carga de la bomba (m).
BHP: Potencia de entrada en la bomba (kW)
El subíndice 1 indica la condición inicial de operación y el subíndice 2 la condición final.
Ron Carson [10], recomienda en entonces utilizar una curva de afinidad que intercepte el sistema en la condición final, lo cual es la base para el desarrollo del procedimiento analítico desarrollado en este artículo.
2.2. Curva característica del sistema hidráulico
El sistema se caracteriza por un modelo bajo la condición de régimen permanente y turbulento de la forma [3].
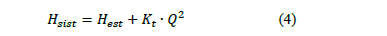
Donde:
Hsist : Carga del sistema (m).
Hest: Carga estática del sistema (m)
Kt : Coeficiente de resistividad de la tubería (s2/m5)
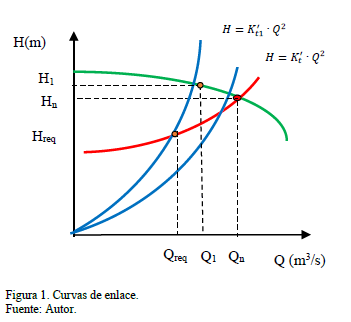
En este procedimiento, basado en la propuesta realizada por Carson [10], se definen como curvas de enlace, aquellas, que sin carga estática, contienen los puntos de operación del sistema de bombeo en condición inicial y final. Por tanto de la ecuación (4) para condiciones de régimen turbulento, para el valor de flujo requerido (Qreq) se obtiene la carga requerida (Hreq) en dicho punto y se cumple que:
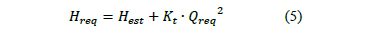
Para la curva de enlace (Fig.2):

Siendo K't la constante ficticia de la tubería representada por la curva de enlace.
En condiciones nominales de operación, el valor de flujo es el correspondiente al valor nominal (Qn), igualando ambas expresiones (Ec.4 y Ec.6) despejando el valor de K't, para la curva de enlace:

De la misma forma para una nueva condición de flujo requerido por el sistema (Qreq), se cumple para la curva de enlace:
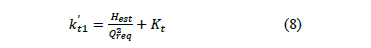
En la curva de enlace (Fig. 1), partiendo del origen de coordenadas, estará contenido el punto que se corresponde con el valor deseado de flujo y carga (Qreq, Hreq) y la misma se intercepta con la ecuación característica de la bomba en el punto (Q1,H1) donde se cumple:
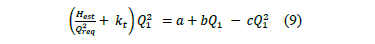
Cuando un sistema de bombeo es estrangulado con el objetivo de reducir los requerimientos de flujo del proceso, la carga del motor eléctrico que acciona la bomba cambia y consecuentemente ocurren cambios en su velocidad de rotación. Sus parámetros de comportamiento deben ser reajustados a fin de realizar un cálculo más exacto de la potencia eléctrica demandada
La potencia demandada por la bomba se expresa como:
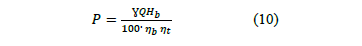
Donde:
P: Potencia demandada (kW)
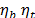 : Eficiencias de la bomba y la transmisión.
: Eficiencias de la bomba y la transmisión.
La definición de las curvas de enlace permitirá mediante el cálculo iterativo la determinación de los cambios de carga y velocidad que ocurren en la bomba centrífuga cuando el sistema es estrangulado mediante válvulas para obtener el flujo requerido por el proceso y cuando es empleado un variador de frecuencia con este fin.
2.3. Ejemplo de aplicación
El procedimiento ha sido aplicado en un sistema de bombeo de guarapo del CAI Hermanos Almejeiras de Villaclara. El sistema está conformado por tres bombas de idénticas características. Los datos nominales de dichas bombas son:
Flujo Nominal (Qn) - 0.058m3/s.
Carga Nominal (Hn) - 52m
Eficiencia Nominal (hb) - 88%
Velocidad Nominal (N) - 1775rpm.
Datos del motor eléctrico.
Potencia Nominal (Pn) - 60hp
Voltaje Nominal (Vn) - 460V
Corriente Nominal (In) - 72A
Eficiencia Nominal (hn) - 91.6%
Velocidad Nominal - 1775 rpm.
Factor de Potencia Nominal (cosqn) - 89%
Mmax/Mnom - 2.26
Los datos de flujo y carga para la obtención de la ecuación característica de la bomba:
Utilizando la función"polyfit": del Matlab 5.3 para el ajuste de curvas, basada en el método de los mínimos cuadrados se obtiene, el polinomio de la ecuación característica de la bomba:
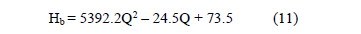
El cálculo del sistema de tuberías consiste en hallar el valor la función H=f(Q) que caracteriza al mismo, para lo cual es necesario determinar el valor de la constante Kt (ecuación .1) que depende del estado en que se opera el sistema hidráulico. El valor del flujo estará en función de los requerimientos del proceso tecnológico y este puede ser obtenido estrangulando el sistema o variando la velocidad del motor manteniendo el sistema a válvula abierta. Para el sistema analizado, partiendo de la información de los especialistas como resultado del cálculo del sistema de tuberías, se tiene que:
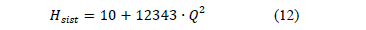
La potencia demandada por la bomba en condiciones nominales de operación se obtiene aplicando la Ec.10
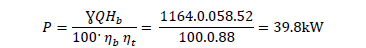
Para calcular el flujo requerido por el proceso se realiza un balance de masa a partir del plan de molida, de los por cientos de fibra en la caña, el bagazo y la cantidad de agua suministrada. En esta aplicación el flujo de jugo mezclado requerido para una capacidad de molienda del 90% es de 0.048 m3/s con un factor de seguridad del 15%. Para este valor de flujo requerido, la carga requerida es de 59.9 m y la eficiencia de la bomba para esta condición es 85.88%.
La aplicación de las leyes de afinidad para esta nueva condición de requerimiento de flujo del sistema daría como resultado
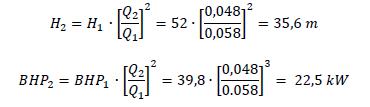
El punto de operación para un flujo de 0,048 m3/s y una carga de 35,6 m no intercepta la curva del sistema y se encuentra distante del valor de la carga de la bomba en el intervalo de operación de la misma lo que demuestra que el valor de potencia obtenido es incorrecto y consecuentemente el cálculo del ahorro de energía obtenido la utilizar un AEFV no es el real.
A partir de la ecuación (4) se determina el valor de la constante para la curva de enlace en condiciones nominales K't.
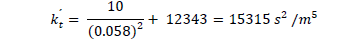
En el punto de operación en condiciones de velocidad variable (Qreq, Hreq), determinar el valor de la constante de la curva enlace del sistema (kt1' Fig.1) aplicando la ecuación (8).
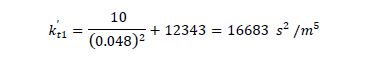
Determinar el valor de Q1 aplicando la ecuación (9)
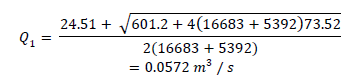
Para esta condición evaluando en la ecuación característica de la bomba ec. (11) se obtiene que el valor de la carga es 92.5 m.
A partir del valor de velocidad nominal, por las relaciones de flujo capacidad entre el punto (Q1,H1) y (QreqHreq), aplicando la leyes de afinidad a través de las curvas de enlace son determinados los valores de velocidad y carga requeridos para la nueva condición de operación:
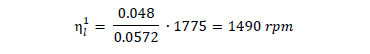
Para esta nueva condición el valor de carga obtenido es de 65,2 m el cual está dentro del rango de operación de la bomba.
La potencia demandada por la bomba en esta nueva condición es de 24,4 kW. Nótese como la diferencia de la potencia demandada por la bomba seria de 2,1 kW, lo cual implicaría que se estarán sobrestimando los niveles de ahorro de energía ya que en un tiempo promedio de 16 horas diarias durante los 140 días de zafra azucarera del año representarían 12,2 MW.h anuales.
3. Conclusiones
El procedimiento analítico desarrollado permite disminuir en gran medida la incertidumbre en el cálculo del ahorro de energía que se deriva de la aplicación de (EVFD) en el control del flujo en los sistemas centrífugos de bombeo, con una justificada adecuación de las leyes de afinidad a sistemas con alta carga estática. Se demuestra como una inadecuada aplicación de las mismas puede traer consigo cálculos erróneos que pueden propiciar una incorrecta valoración económica en los estudios de factibilidad para la introducción de este equipamiento altamente costoso en las actividades industriales y los servicios.
Referencias
[1] Almeida, A.T., Fonseca, P., Falkner, H. and Bertoldi, P., Market transformation of energy-efficient technologies in the EU. Energy Policy, 31, pp. 563-575. 2003. DOI: 10.1016/S0301-4215(02)00100-3. [ Links ]
[2] Jagtap, S.P. and Pawar, A.N., Energy efficiency evaluation in pumping system. Modern Mechanical Engineering, 3(4), pp. 171-180, 2013 [ Links ]
[3] Vodovozov, V., Gevorkov, L. and Raud, Z., Modeling and analysis of pumping motor drives in hardware-in-the-loop environment. Journal of Power and Energy Engineering, 2(10), pp. 19-27, 2014. DOI: 10.4236/jpee.2014.210003. [ Links ]
[4] Coelho, B. and Andrade-Campos, A., Efficiency achievement in water supply systems-A review. Renewable and Sustainable Energy Reviews, 30, pp. 59-84, 2014 [ Links ]
[5] Su, C.L., Chung, W.L. and Yu, K.T., An energy-savings evaluation method for variable-frequency-drive applications on ship central cooling systems. Industry Applications, IEEE Transactions on, 50(2), pp. 1286-1294. 2014. [ Links ]
[6] Jones, W.V., Motor selection for centrifugal pump applications made easy. In Pulp and Paper Industry Technical Conference (PPIC), Conference Record of 2011 Annual IEEE, pp. 140-150, 2011. [ Links ]
[7] Ahonen, T., Tamminen, J., Ahola, J. and Kestilä, J., Frequency-converter-based hybrid estimation method forthe centrifugal pump operational state. IEEE Transactions on Industrial Electronics, 59, pp. 4803-4809, 2012. DOI: 10.1109/TIE.2011.2176692 [ Links ]
[8] Finnemore, J.E. and Franzini, J.B., Fluid Mechanics. McGraw-Hill, 2002. [ Links ]
[9] Messina, J.P., Pump Handbook. Vol. 3. New York: McGraw-Hill, 1986. [ Links ]
[10] Carlson, R., The correct method of calculating energy savings to justify adjustable-frequency drives on pumps. IEEE Transactions on Industry Applications, 36(6), pp. 1725-1733, 2000. [ Links ]
[11] Crane, Flujo de fluidos en válvulas, accesorios y tuberías. McGraw-Hill, 1987. [ Links ]
M.S. Santos-Azevedo, es graduado en Matemática en 1985, en Procesamiento de Datos en 1999, ambos de la Universidad Federal de Amazonas, Brasil y MSc. Ingeniería Eléctrica en 2006, de la Universidad Federal de Campina Grande, Brasil. Es profesor asistente de la Universidad del Estado de Amazonas (UEA), Brasil. Tiene experiencia en el área de Sistemas Computacionales con énfasis en Modelos Analíticos y simulación de sistemas. Es coordinador de proyectos en ITEGAM. Doctorado en Ing. Eléctrica UFPA, 2014. ORCID 0000-0002-0611-2906
C.A. de Leon-Benitez, es Ing Eléctrico Graduado UCLV en 1983. Profesor Titular de la Facultad de Ing. Eléctrica de la UCLV. Jefe de departamento en el periodo 2008-2012. Especialista en sistemas Eléctricos Industriales, Maquinas eléctrica y accionamientos. Colaborador del Instituto de Tecnología Galileo del Amazonas. ORCID 0000-0003-2749-1134
J.Cabral-Leite, es graduado en Matemática en 1987 de la Universidad Federal de Rondónia (UNIR), Brasil; en Ingeniería en Producciones Eléctricas, en 2006 de la Fundación Centro de Análisis Pesquisa e Innovación Tecnológica - FUCAPI, Brasil; MSc. en Ing. Industrial y en Sistemas en 2001, de la Universidad Federal de Santa Catarina (UFSC), Brasil y Dr. en Ing. Eléctrica en 2013, de la Universidad Federal de Pará (UFPA), Brasil. Es Director Presidente e investigador del Instituto de Tecnología y Educación Galileo de la Amazonía (ITEGAM), Brasil. Sus áreas de interés incluyen: calidad de la energía, análisis, diseño y optimización de sistemas eléctricos de potencia. ORCID 0000-0002-1337-3549
I. Perez Abril, es Ing Eléctrico Graduado UCLV en 1984. Profesor Titular de la Facultad de Ing. Eléctrica de la UCLV. Actualmente Director del Centro de Estudios Electroenergéticos de la UCLV. Especialista en Sistemas Eléctricos Industriales y Calidad de la Energía Colaborador del Instituto de Tecnología Galileo del Amazonas. ORCID 0000-0001-9547-6615