Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.199 Medellín Dec. 2016
https://doi.org/10.15446/dyna.v83n199.51385
DOI: http://dx.doi.org/10.15446/dyna.v83n199.51385
Gaussian clarification based on sign function
Clarificación gaussiana basado en la función signo
José de Jesús Medel-Juárez a, Mario Espinosa-Santiago a & José Luis Fernández-Muñoz b
a Centro de Investigación en Computación, Instituto Politécnico Nacional, México. jjmedelj@yahoo.com.mx, xxmesxx@gmail.com
b Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada, U. Legaría, Instituto Politécnico Nacional, México. jlfernandezmu@gmail.com
Received: June 18th, 2015. Received in revised form: March 16th, 2016. Accepted: May 25th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This paper presents a clarification model in the fuzzy sense based on the Membership Inverse Function (MIF), in Control Theory. It is considered as an identification and requires bounded input and output signals. The sign function and its derivative is regarded as a Gaussian function into the mathematical Membership description. Specifically, the sign function considers the difference between the absolute state variable values and its centroid, rather than remaining in the triangle inequality. Therefore, the theoretical result applied in Matlab® using the reference values as an identification process in an Auto Regressive Moving Average (ARMA) (1, 1) model describes the performance. The clarification converging in almost all points of the desired signal depends on the different initial conditions. The convergence obtained by the functional error built by the second probability moment was also used and applied in the same software giving an illustrative description.
Keywords: Clarification; Fuzzy Logic; Identification; Stochastic Process.
Resumen
Este artículo presenta un modelo de clarificación en el sentido difuso basado en la función de membresía inversa como proceso de identificación para un sistema tipo caja negra con Una Entrada y Una Salida (UEUS). La función signo y su derivada para la función gaussiana, permite la descripción matemática del estado a identificar. Específicamente, la función signo aplica la diferencia entre los valores absolutos de la variable de estado y su centroide, en vez de la desigualdad del triángulo. El resultado teórico estuvo aplicado en Matlab®, usando como valores de referencia a los resultados del modelo Auto-Regresivo de Promedios Móviles (ARPM) (1, 1); permitiendo la clarificación y su convergencia en casi todos los puntos a la señal de referencia con diferentes condiciones iniciales entre ellos. La convergencia de forma ilustrativa se describió por el funcional del error a través del segundo momento de probabilidad usando el mismo software.
Palabras clave: Clarificación; Lógica Difusa; Identificación; Proceso Estocástico.
1. Introduction
"The world is not black and white but only shades of gray." In 1965, Zadeh [1] wrote a seminal paper in which he introduced fuzzy sets with smooth boundaries. These sets are considered gray areas rather than black and white in contrast to classical sets, which form the basis of Boolean or binary logic. Fuzzy set theory and fuzzy logic are convenient tools for handling imprecise, or unmolded data in intelligent decision-making systems. It has also found many applications in the areas of information sciences and control systems.
In many science areas, the identification process used internal system states for description, reconstruction or prediction. The techniques developed, give the average answer regarding its internal states such as the centroid method (in fuzzy logic) or the analytical methods based on stochastic gradient. The identification is known as clarification in the fuzzy logic sense [2]. The clarification methods according to performance have similar structures [3], and generate an equivalent signal compared with a reference, without indicating the associated properties [4]. The common strategies such as Gaussian Membership Function (GMF) and Polynomial Transformation (PT) are combined, obtaining better performance compared with the existing algorithms [5]. Another strategy is the distance between two fuzzy sets resulting in a clarification value without the index determining the original fuzzy number [6]. Control Theory (CT) suggests the Fuzzy Clarification Method (FCM) [7] instead of Least Squares Method (LSM) [8-9], Instrumental Variable (IV) [10-11], Forgetting Factor (FF) [12-13], Stochastic Gradient (SG) [14-17], Kalman Filter (KF) [18-19], and Deconvolution [20-23]. The control systems commonly have unwanted conditions or operations and the clarification process involved gives poor results because its average answer requires using Artificial Neural Networks (ANN) with stability conditions applied during the identification process [24], obtaining better results in simulation [25-26]. In [27], a clarification algorithm was applied into a fuzzy adaptive controller deciding it necessary to know the internal state value, bounded by a GMF. The Membership Inverse Function (MIF) transforms the fuzzy results into identified states without indicating the technique used [28]. The statistical properties such as Mean, and Standard Deviation according to [27-32] accomplish the Main Membership Function (MMF).
The Membership Inverse Function (MIF) as a clarification process approximating this result to the real reference value.
According to previous results, we develop the clarification process for stochastic signals using the signal system sign function considered bounded by a Membership Gaussian Function (MGF). Section 2 gives the main results. Section 3, presents the simulations and in the conclusions are developed in Section 4 describing the advantages and the references applied.
2. Main results
The clarification process has a natural description using the sign function properties applied into Membership Gaussian Function (MGF) according to Theorem 1. Thus, the Black-box system response is described through the clarification process knowing only the Membership Function (MF) and its two first probability moments.
With 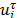 as the input and
as the input and 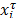 the output, satisfying
the output, satisfying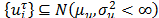 ,
,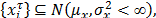 here,
here, 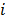 is the sequence index and
is the sequence index and 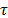 is the time system state with
is the time system state with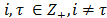 .
.
Theorem 1. Let 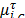 be described in eq. (1), as the Membership Gaussian Function (MGF) for a fuzzy system.
be described in eq. (1), as the Membership Gaussian Function (MGF) for a fuzzy system.
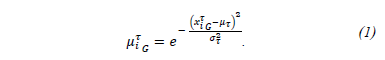
The clarification state 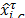 in eq. (2) is based on sign function accomplished with
in eq. (2) is based on sign function accomplished with 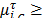 0,
0,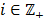 .
.
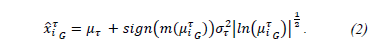
With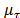 ,
, 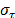 are the Centroid and Standard Deviation respectively, with a time occurrence system state
are the Centroid and Standard Deviation respectively, with a time occurrence system state 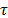 into sequence states
into sequence states 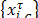 , allows associating a Membership Function (MF)
, allows associating a Membership Function (MF) 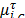 . With slope
. With slope 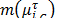 and
and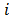 the sequence index.
the sequence index.
Proof. Let eq. (3) be a description of sign function
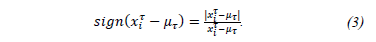
The 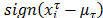 considering in eq. (4), is a Membership Gaussian Function (MGF) with slope
considering in eq. (4), is a Membership Gaussian Function (MGF) with slope 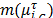 , instead of absolute value.
, instead of absolute value.
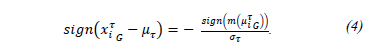
Eq. (5) applies the logarithm of the Gaussian function according to eq.(3).
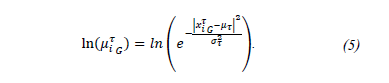
Eq. (6) presents the simplified result of eq. (5).
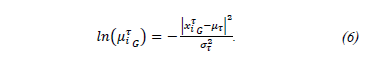
Eq. (7), without denominator having the equality to 0.
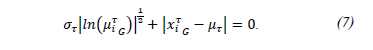
Eq. (8) presents the evaluation of 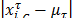 as
as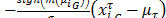 in eqs. (3) and (4) into eq. (7).
in eqs. (3) and (4) into eq. (7).
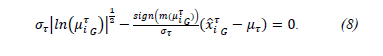
Eq. (9) develops the clarification (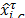 ) with respect to Membership Gaussian Function in agreement to eq. (8).
) with respect to Membership Gaussian Function in agreement to eq. (8).
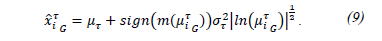
3. Simulation
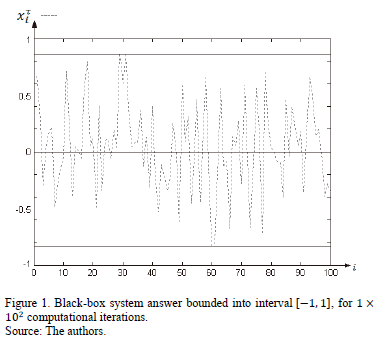
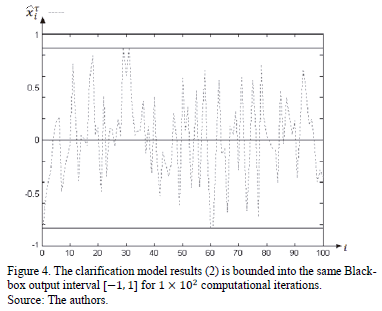
The digital Black-box system described by an ARMA (1, 1) technique [15] with State Space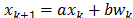 ; its evolution is depicted in Fig. 4 for
; its evolution is depicted in Fig. 4 for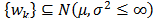 .
.
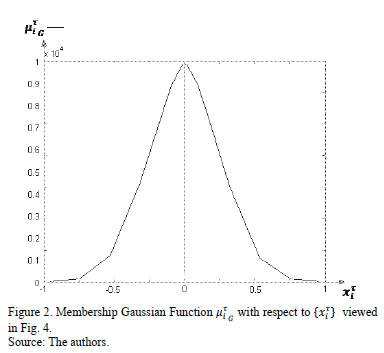
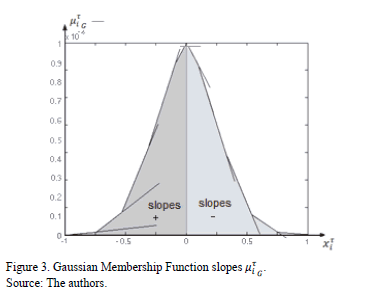
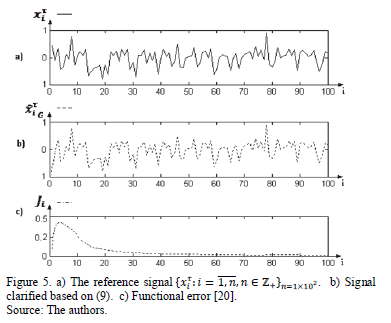
The system proposed bounded by a Normal Distribution [32] is depicted in Fig. 2 with a Membership Gaussian Function (MGF) [33]. The slopes presented in Fig. 3 used the eqs. (3) and (4) into MGF. Fig. 5 shows the clarification state (2) 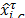 justifying Theorem 1 through (9).
justifying Theorem 1 through (9).
Fig. 2 shows the Gaussian Membership function 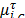 based on ARMA (1, 1) technique.
based on ARMA (1, 1) technique.
Fig. 3 presents the slopes 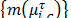 according to eq. (3) and taking into account the information content in Fig. 2.
according to eq. (3) and taking into account the information content in Fig. 2.
Fig. 4, describes the clarification result viewed by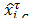 , function.
, function.
Fig. 5, includes the system evolution and its clarification, observing both signals converging regardlees of different initial conditions.
4. Conclusions
The output system bounded by a Membership Gaussian Function (MGF) required a novel clarification technique justified in (9). The model developed and applied considered eqs. (4) and (5) properties applied in (8). The defuzzification strategy used a unit vector concept and its derivate properties applied on Membership Function (MF), achieving the clarification strategy. The theoretical results were developed
by the stochastic system bounded by a Gaussian distribution. The identification process or clarification consists of the Membership Inverse Function (MIF) developed in an analytical manner in eq. (2) and validated theoretically in eq. (9).
Therefore, this description for the clarification process was based on Membership Gaussian Inverse Function (MGIF) with the sign function and its derivative properties, obtaining the description 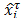 state.
state.
References
[1] M. Oussalah, On the compatibility between defuzzification and fuzzy arithmetic operations, Fuzzy Sets and Systems, 128(2), pp. 247-260, 2002. [ Links ]
[2] Saletic., D.Z. and Popovich.,U., On possible constraints in applications of basic defuzzification techniques, Proceeding of the 8th Seminar on neural network applications in electrical engineering, NEUREL, pp. 225-230, 2006. [ Links ]
[3] Jung, S.H., Cho., K.H., Kim., T.G. and Park., K.H., Defuzzification method for multi-shaped output fuzzy sets, Electronics Letters, 30(9), pp. 740-742, 1994. [ Links ]
[4] Jiang., T. and Li., Y., Generalized defuzzification strategies and their parameter learning procedures, IEEE Transactions on Fuzzy Systems, 4(1), pp. 64-71, 1996. [ Links ]
[5] Ma, M., Kandel, A. and Friedman, M., A new approach for defuzzification, Fuzzy Sets and Systems, 111(3), pp. 351-356, 2000. [ Links ]
[6] Runkler, T.A., Extended defuzzification methods and their properties, Proceedings of the 5th IEEE International Conference on Fuzzy Systems, 1, pp. 694-700, 1996. [ Links ]
[7] Liu, F., Wang, J. and Peng, Y., A new approach to parameters identification of fuzzy regression models, Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery, 1, pp. 127-131, 2008. [ Links ]
[8] Mastorocostas, P. and Theocharis, J., Orthogonal least squares fuzzy modeling of nonlinear dynamical systems, Proceedings of the 6th IEEE International Conference on Fuzzy Systems, 2, pp. 1147-1152, 1997. [ Links ]
[9] Dai, H., Sinha, Naresh, K., Iterative instrumental variable method for robust identification of systems, IEEE Transactions on Industrial Electronics, 42(5), pp. 480-486, 1995. [ Links ]
[10] Yinao, W., Aiqing, R. and Zhihui. Z., The numerical simulation of improving parameter estimation by instrumental variable method, Proceeding of the IEEE International Conference Grey Systems and Intelligent Services (GSIS), pp. 811-815, 2011. [ Links ]
[11] Chen-Sen, O., Naijing, K. and Po-Jen, C., Recursive SVD-Based Least squares algorithm with forgetting factors for neuro-fuzzy modeling, Proceeding of the 14th International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), pp. 575-580, 2013. [ Links ]
[12] Paleologu, C., Benesty, J. and Ciochina, S., A robust variable forgetting factor recursive least squares algorithm for system identification, IEEE Signal Processing Letters, 15, pp. 597-600, 2008. [ Links ]
[13] Medel, J.J. and Zagaceta, M.T., Estimación-identificación como filtro digital integrado: descripción e implementación recursiva. Rev. Mex. Fis., 56(1), pp. 1-8, 2010. [ Links ]
[14] Ding, F., Liu, G. and Liu., X.P., Partially coupled stochastic gradient identification methods for non-uniformly sampled systems, IEEE Transactions on Automatic Control, 55(8), pp. 1976-1981, 2010. [ Links ]
[15] Chang, S.L. and Ogunfunmi, T., Stochastic gradient based on 3rd order Volterra system identification by nonlinear Wiener adaptive algorithm, IEE Proceedings of the Vision, Image and Signal Processing, 150(2), pp. 90-98, 2003. [ Links ]
[16] Bershad, N.J., Celka, P. and Vesin, J., Stochastic analysis of gradient adaptive identification of nonlinear systems with memory for Gaussian data and noisy input and output measurements, IEEE Transactions on Signal Processing, 47(3), pp. 675-689, 1999. [ Links ]
[17] Wei, C.L., Tsai, J.S.H., Guo, S.M. and Shieh., L.S., Universal predictive Kalman filter based on fault estimator and tracker for sampled-data non-linear time-varying systems, Control Theory & Applications, IET, 5(1), pp. 203-220, 2011. [ Links ]
[18] Chafaa, K., Ghanai, M. and Benmahammed, K., Fuzzy modeling using Kalman filter, Control Theory & Applications, IET, 1(1), pp. 58-64, 2007. [ Links ]
[19] Medel, J.J. y García, C.V., Estimación de parámetros usando la deconvolución y la pseudo-inversa: descripción e implementación recursiva. Rev. Mex. Fis., 56(1), pp. 54-60, 2010. [ Links ]
[20] Erdogmus, D., Hild., K.E., Principe, J.C., Lazaro, M. and Santamaria, I., Adaptive blind deconvolution of linear channels using Renyi's entropy with Parzen window estimation, IEEE Transactions on Signal Processing, 52(6), pp. 1489-1498, 2004. [ Links ]
[21] Chen, L. and Kim-Hui, Y., A soft double regularization approach to parametric blind image deconvolution, IEEE Transactions on Image Processing, 14(5), pp. 624-633, 2005. [ Links ]
[22] Depeyrot, M., Linear System identification using real-time deconvolution, IEEE Transactions on Computers, C-1(12), pp. 1139-1145, 1970. [ Links ]
[23] Meng-Xin, L., Cheng-dong, W. and Feng, J., A vision-based inspection system using fuzzy rough neural network method, Proceeding of the International Conference on Machine Learning and Cybernetics, pp. 3228-3232, 2006. [ Links ]
[24] Sivanandam, S.N., Deepa, S.N. and Sumathi, S., Introduction to Fuzzy logic using MATLAB®, Springer, pp. 95 - 108, 2007. [ Links ]
[25] Nguyen, H.T., Prasad, N.R., Walker., C.L. and Walker, E.A., A 1st course in Fuzzy and neural Control, (Chapman and Hall/CRC, (2002), Ed. 1, pp. 120-123. [ Links ]
[26] Kosinski, W., Evolutionary algorithm determining defuzzyfication operators, Engineering Applications of Artificial Intelligence, 20(5), pp. 619-627, 2007. [ Links ]
[27] Urbanski, K. and Wasowski, J., Fuzzy measurement theory, Measurements, 41(4), pp. 391-402, 2008. [ Links ]
[28] Jang, J.S.R., Sun, C.T. and Mizutani, E., Neuro-fuzzy and soft computing: a computational approach to learning and machine intelligence, Prentice-Hall, 1997, pp. 24 - 28. [ Links ]
[29] Shin, Y.C. and Xu, C., Intelligent systems: modeling, optimization, and control. Section 2.1.3. CRC Press, 2008. [ Links ]
[30] Slotine, J.J. and Li, W., Applied nonlinear control, Prentice-Hall, 1991, 1, pp. 290-306. [ Links ]
[31] Shtessel, Y., Edwards, C., Fridman, L. and Levant, A., Sliding Mode control and observation, Control Engineering, Birkhäuser, pp. 18-19, 2013. [ Links ]
[32] Velásquez-Henao, J.D. and Branch-Bedoya, J.W., Examples in the classroom: Pattern classification using the R language, DYNA, 79(173), pp. 81-88, 2012. [ Links ]
[33] Velásquez-Henao, J. D., Rueda-Mejía, V.M. and Franco-Cardona, J.D. Electricity demand forecasting using a SARIMA- multiplicative single neuron hybrid model, DYNA, 80(180), pp. 4-8, 2013. [ Links ]
[34] Roy-Chowdhury, S. and Pedrycz, W., A survey of defuzzification strategies, Int. J. Intel. Syst, pp. 679-695, 2001. [ Links ]
J. de J. Medel-Juárez, is a Professor working on- intelligent estimation and identification applied in hybrid filters. He is an Aeronautics Engineer (1994), MSc. in sciences in Automatic Control (1996), and also a PhD in Automatic Control (1998), Member of National Council for Science and Technology (1999), member of the Mexican Academy of Sciences. Actually, he is a Full Time Professor and Researcher in the Computer Research Center (CIC). His researches include Digital filtering, Control, Real-time, among others. ORCID: 0000-0002-1257-1711
M.Espinosa-Santiago, is a MSc. in Computer Research Center (CIC) and Eng. in Electronics and Communications at the Mechanical and Electrical School at National Polytechnic Institute (ESIME Zacatenco IPN). Currently he works at the Technical Center for Research and Development Carso, (CTQ-CIDEC). ORCID: 0000-0003- 0449-9382
J.L. Fernández-Muñoz, is a Full Time Professor working on Applied Intelligent Systems. He is PhD. in Physics and has MSc. in Physics (1998). Member of the National Researchers System. He is a researcher at Research Center of Science and Advanced Technology (CICATA-IPN) in the Laboratory of Condensed Matter. ORCID: 0000-0002-2039-3222