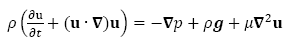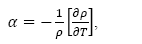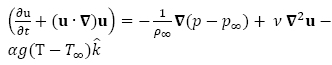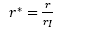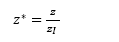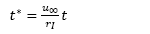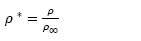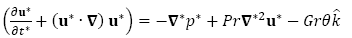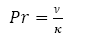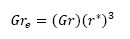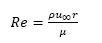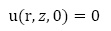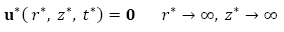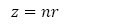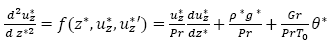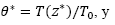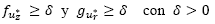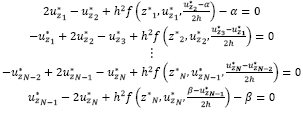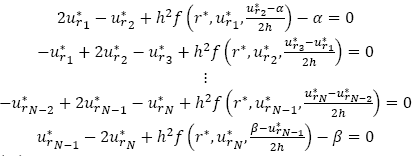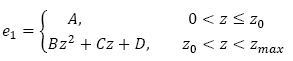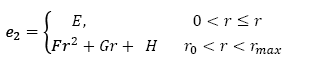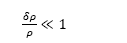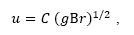1. Introducción

Un termal es una región de aire ascendente en las altitudes más bajas de la atmósfera de la tierra, Fig. 1. Estas térmicas son creadas por el calentamiento desigual de la superficie de la tierra por radiación solar, es decir, en el caso de la atmósfera terrestre el sol calienta el suelo que a su vez calienta el aire sobre la superficie de la tierra y, así, produce un termal; las zonas oscuras como las ciudades son fuentes de termales [¹].

Los termales son un problema abierto en física y meteorología dada la dificultad para poder definirlos y modelarlos, esta dificultad está basada en la no existencia de una teoría que lo modele. La convección natural es una de las teorías que trata de estudiarlo y consiste en el movimiento de masa producido por factores como la acción de fuerzas de cuerpo; existen varias teorías [¹] que explican este fenómeno. En 1947 Taylor y Sutton formularon la idea de que los termales son como burbujas que se mezclan con el aire circundante, estas burbujas se consideran como esferas de aire caliente, idea que se aplica principalmente a la nube superior en forma de hongo que se produce en la explosión de la bomba atómica [²].

Una teoría propuesta por Scorer y Ludlam [³] en 1953 propone la existencia de una unidad principal de convección, la cual puede interactuar con otras unidades permitiendo que se pueda explicar fenómenos más complejos. Los puntos calientes en la teoría de Scorer y Ludlam ya no toman un papel central y, de la misma manera, la capa del termal adiabática no se considera como una capa clara, esta capa adiabática se considera en toda su extensión como algo poco definido. De otra parte, el estudio del viento toma un papel central como lo muestra Sreenivasan y Bershadskii [⁴] en el 2010, donde estudia las características del viento medio en la convección térmica, especialmente la reversión abrupta de su dirección en los casos donde el número de Rayleigh (Ra=Gr Pr) es alto.

Son varios los casos en la naturaleza donde los termales desempeñan un papel importante, Scorer [⁵] en 1957 estudia el movimiento de un fluido producido por las fuerzas de flotabilidad, con el objetivo de poder simular el termal producido en la atmósfera; lo interesante de este trabajo es el método experimental empleado por Scorer, dado que produce a pequeña escala un termal propio de la atmósfera que en promedio tiene una altura de ochocientos metros, Scorer [⁶] en 1958 estudió también el problema de la convección producida por el humo expulsado por las chimeneas, un ejemplo estándar de un termal producido por una fuente puntual. Schmidt [⁷] en 1941 mostró como la anomalía de temperatura, velocidad vertical y la anchura del chorro, podrían por un punto aislado o línea fuente de calor expresarse como potencias de la altura por encima de la fuente. El método de la solución se deriva a partir del estudio de la capa límite y las estelas turbulentas de cilindros, del mismo modo se ha aplicado a la convección sobre una superficie plana calentada uniformemente. El fenómeno de convección no solo se da en la atmósfera, también en el océano como lo muestra Rahmstorf en 2001 [⁸], en el cual realiza un estudio teórico.

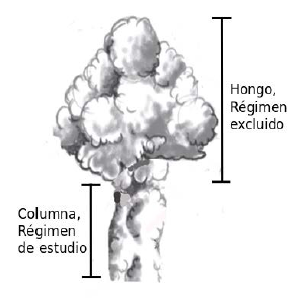
Fuente: Los autores.

Figura 1 Forma de un termal en acenso, donde la sección columna representa el dominio de estudio del flujo, y la sección hongo representa un dominio donde la velocidad ascensional media se asume sustancialmente más pequeña que la velocidad en la columna.  

En este artículo se desarrolla un código basado en ROOT(A Data Analysis Framework), el cual es un conjunto de clases basados en C++ desarrollado por el proyecto CERN, que para un instante de tiempo permite implementar el método de diferencias finitas mostrando la velocidad de las partículas del termal en función de la altura o radio de éste, para valores grandes del número de Grashof, el cual es el cociente entre la fuerza de boyamiento y las fuerzas viscosas (la propiedad que ocasiona los esfuerzos cortantes en un fluido). De la misma manera, se estudia la velocidad del termal como función del radio de la burbuja principal del termal, para valores grandes del número de Grashof. El método de las diferencias finitas es usado debido a las enormes dificultades que conlleva la solución del modelo del termal que se quiere estudiar. El problema principal del método numérico está en la solución de la ecuación de Navier- Stokes, Bell y Marcus [⁹] en 1990 propusieron un método numérico para resolver el problema de un fluido con densidad variable, y en 1989 [¹⁰] solucionaron el problema para la ecuación de Navier-Stokes para un fluido incompresible. Un estudio computacional de la vorticidad y el campo de temperaturas de un termal esta dado en el artículo de Marcus y Bell en 1992 [¹¹].

Vulfson y Borodin [¹²] en el 2008 proponen un modelo integral de un chorro espontáneo cuasi-estacionario que admite una solución analítica exacta en un conjunto de corrientes térmicas convectivas para un elemento de convección aislado.

El problema de convección libre también es tratado de una forma computacional, esta vez utilizando el método de elemento finito para problemas de convección térmica, Jan, Young y Chiu [¹³]. La convección no es exclusiva de la atmósfera de un planeta como la tierra, como lo muestra Kostyk [¹⁴] en el 2011, puesto que se ha evidenciado en el sol y en Venus, Izakov 2002 [¹⁵].

En la siguiente sección se plantea el modelo teórico del problema, posteriormente se muestran los detalles del método numérico implementado y por último se analizan los resultados.

2. Dinámica del termal

El flujo es modelado por la ecuación de Navier-Stokes considerando la aproximación de Boussinesq en la cual las variaciones de la densidad relativa, δ_ρ, son pequeñas, es decir, 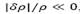, siendo ρ la densidad media, donde solo se tiene en cuenta los efectos de la variación de la densidad en el término de boyamiento de la ecuación de Navier-Stokes. La aproximación de Boussinesq se aplica a problemas en los cuales el número de Mach para fluidos es menor que 1 / 3 y la escala de altura es pequeña, es decir, el cambio neto en magnitudes como la densidad es pequeño [¹⁶].

2.1. Ecuación de continuidad

La aproximación de Boussinesq reemplaza la ecuación de continuidad por la condición de incompresibilidad

(1)

Donde u es el campo de velocidad de las partículas de fluido. Lo anterior no significa que la densidad sea constante en la dirección del movimiento, en realidad quiere decir que los términos de del gradiente de velocidad dominan sobre 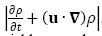. Los efectos de compresibilidad son despreciables cuando el número de Mach, Ma < 0.3 [¹⁶]

2.2. Ecuación de momentum

Dada la condición de incompresibilidad, la ecuación de Navier-Stokes está dada por

(2)

Donde ρ es la densidad y µ la viscosidad. Si se ubica una región donde la temperatura sea constante en un fluido estacionario, y dado que el coeficiente de dilatación volumétrico se define como

(3)

la variación de la presión en la convección libre es generalmente pequeña y, además, los efectos de la presión en α también son pequeños [¹⁷]. En otras palabras, α en la convección libre se puede asumir independiente de ρ. También se asume que la forma con que la densidad depende de la temperatura, ρ(T), es lineal, por tanto la ecuación de momentum con ayuda de la aproximación de Boussinesq se escribe como:

(4)

Donde T es la temperatura, v, la viscosidad cinemática, α, coeficiente de dilatación térmica, g, la aceleración gravitatoria y ρ∞ una densidad de referencia. Para adimensionalizar la ecuación (4), se necesita cantidades características (parámetros) constantes del fluido y el campo de temperaturas, estas cantidades son y r ₁ . Donde r ₁ es el radio inicial del termal. Con los cuales se pueden definir los parámetros adimensionales:

(5)

(6)

(7)

(8)

(9)

(10)

Donde Z_I es la altura inicial del termal y T₀ es la temperatura inicial al interior del termal. ()* Indica variables adimensionales.

De lo anterior, se puede escribir la ecuación (4) en forma adimensionalizada

(11)

(12)

Donde Pr es el número de Prandlt, y se definen como

(13)

Donde k es el coeficiente de difusión térmica. El número de Grashof se definen como

(14)

Dada la ecuación (14), el número de Grashof efectivo se define como

(14.1)

Y el número de Reynolds

(15)

Las condiciones iniciales al problema están dadas por

(16)

Y las condiciones de contorno son, con r > 0 y z > 0

(17)

(18)

Para poder escribir la ecuación (11) y (12) en términos del radio del termal se utiliza el resultado descrito por R.S. Scorer[⁵].

(19)

Donde n es un término que se determina experimentalmente y es muy cercano a 4.

3. Modelamiento numérico

Las ecuaciones características para el problema al considerar las componentes cilíndricas en forma separada de (11) y (12), deducidas para el problema usando la relación (19) para desacoplar las componentes vertical y radial son:

(20)

Con

(21)

El problema principal consiste en determinar la velocidad de ascenso vertical de la partícula de fluido sobre el eje z (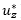) y la velocidad radial de la partícula de fluido a una altura media del termal. Las ecuaciones anteriores son ecuaciones diferenciales de segundo orden no lineales, por tanto es necesario utilizar un método numérico para solucionarlas, y en este caso se utiliza el método de diferencia finita.

Para solucionar las ecuaciones (20) y (21) ƒ y g deben cumplir las siguientes características

1. ƒ , g, las derivadas parciales 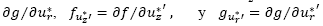son continuas en la región D dado por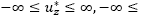 y la region H dado por .

Dado que el termal evoluciona en un entorno donde no existen obstáculos físicos y factores externos: como fuerzas que lo afecten de forma drástica, las velocidades de la partícula 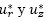no tienen un cambio brusco de un punto en el espacio (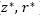) a otro, por tanto se puede decir que y 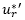son continuas en todo el intervalo D y H, y por lo anterior 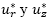son también continuas en las regiones D y H. Dado que la multiplicación de dos funciones continuas es una función continua, los término son continuos, de la misma manera los término 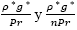son constantes. Por tanto, continúas sobre el dominio D y H. Finalmente, 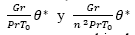son funciones lineales continuas, de manera que sabiendo que la suma de funciones continuas es una función continua ƒ y g son continuas en el intervalo D y H

2. .

Por el teorema de Weierstrass 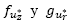tienen un máximo o mínimo absoluto y en este caso 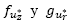tienen un mínimo lo cual garantiza la característica dos.

3. Existen las constantes k y L, con k = 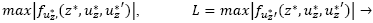, 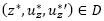y existen las constantes con.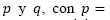

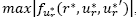
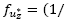
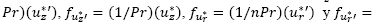
Para poder verificar la característica tres, 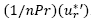. Esto indica que existe un máximo para 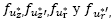porque existe un valor máximo tanto para 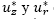como para 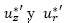ya que son continuas, y con lo anterior se muestra el cumplimiento de la característica tres.

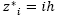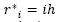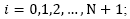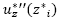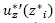En este caso se divide el intervalo [0, A] (donde A es la altura máxima del termal) para la ecuación (20) y el intervalo [0, B] para la ecuación (21 ) (Donde B es el radio máximo del termal ) en N + 1 subintervalos iguales, de ancho cuyos extremos se encuentran en y , para; y suponiendo que la solución exacta tiene una cuarta derivada acotada que permite reemplazar y en la ecuación (20), 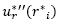y 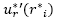en la ecuación (21) y por la fórmula de diferencia central [¹⁸] apropiada para todo i = 1, 2,..., N como en el caso lineal, el método de diferencia resulta cuando se eliminan los términos de error y se emplean las condiciones de contorno, se tiene para todo i = 1, 2,..., N el sistema no lineal de N X N obtenido para solucionar (20) y (21); en este método para (20) es:

(22)

Y para (21)

(23)

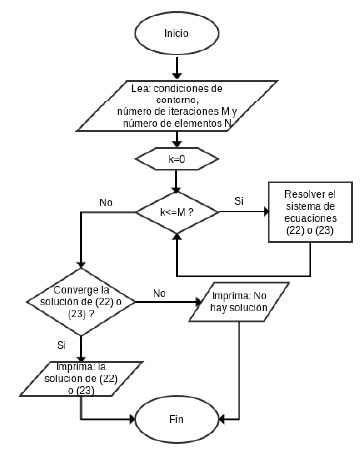
Aplicando el método de Newton [¹⁹] para sistemas no lineales donde se requiere que en cada iteración se resuelva el sistema no lineal N × N, se genera una sucesión de iteraciones (siempre y cuando el sistema de ecuaciones (22) y (23) no sea singular) para que el sistema converja a una solución. Se tiene la ventaja que el sistema de ecuaciones (22) y (23) es una matriz banda de tal forma que se puede aplicar el método de factorización de Crout [²⁰]. A continuación se presenta Diagrama de flujo de código basado en diferencias finitas cuya salida es la velocidad y altura del termal Fig. 2.

4. Resultados y Análisis

Los resultados obtenidos por el código desarrollado son las velocidades de la partícula de fluido, tanto vertical como radial 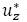y como función de la altura 𝑧 y el radio del termal 𝑟, respectivamente, para distintos valores del número de Grashof efectivo, 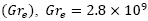Figs. 3 y 6, 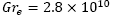Figs. 4 y 7, y 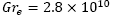Figs. 5 y 8. Los resultados son para termales con altura y radio máximo, de 300, 600 y 900𝑚, respectivamente, que corresponden a las curvas con las letras A, B y C de las Figs. 3 a la 8, se considera constante el número de Prandtl, 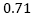y para todos los casos.

Fuente: Los autores

Figura 2 Diagrama de flujo de código basado en diferencias finitas cuya salida es la velocidad y altura del termal 

Fuente: Los autores.

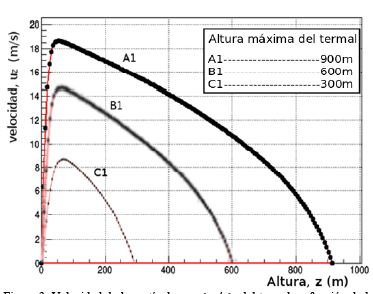
Figura 3 Velocidad de la partícula, 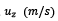del termal en función de la altura del termal, s (m)para un número constante de 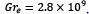, la velocidad máxima alcanzada para las tres curvas en z =75m . 

En la curva A1 de la Fig. 3 se muestra como la velocidad de la partícula de fluido es mayor (antes de alcanzar la altura de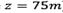) en comparación con las curvas B1 y C2. Los resultados anteriores dan evidencia primaria de como la fuerza boyante en el problema de los termales empieza a tomar un papel preponderante para el estudio dinámico de este sistema en comparación con otras propiedades del fluido, como los efectos viscosos, la temperatura del termal y la viscosidad del medio que lo rodea. En la Fig. 3, se puede observar que en el caso A1 se presenta el crecimiento más rápido de la velocidad con la altura; no obstante los picos de velocidad se alcanzan en un mismo punto de altura z = 75m para A1, B1 y C1.

Fuente: Los autores.

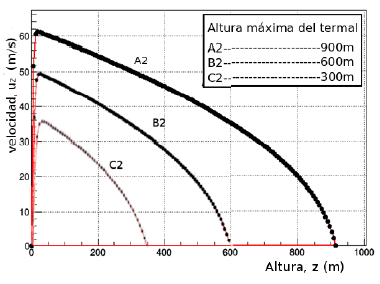
Figura 4 Velocidad de la partícula, 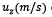del termal en función de la altura del termal, z (m) para un número constante de 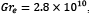, la velocidad máxima alcanzada para las tres curvas en 𝑧=30𝑚. 

Fuente: Los autores.

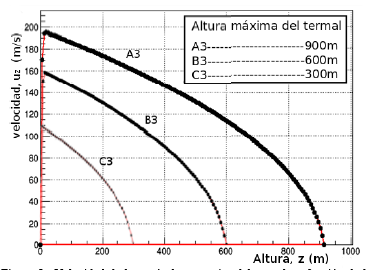
Figura 5 Velocidad de la partícula, 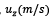del termal en función de la altura del termal, z (m) para un número constante de , la velocidad máxima alcanzada para las tres curvas en z = 10m.  

En la Fig. 4 la manera como disminuye la velocidad en las curvas A2, B2 y C2 es muy parecida a lo que ocurre en la Fig. 3, y también la velocidad máxima para la Fig. 4 para los tres casos (A2, B2 y C2) a una misma altura en este caso de z = 30m.. La velocidad máxima de la curva A2 de nuevo es la mayor en comparación con las curvas B2 y C2 dando un primer indicio de la proporcionalidad de la velocidad máxima alcanzada por una partícula de fluido en un termal y su altura máxima.

Fuente: Los autores

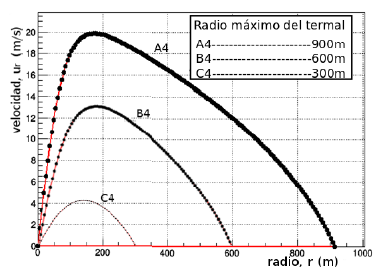
Figura 6 Velocidad de la partícula, 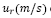del termal en función del radio del termal, r (m) para un número constante de 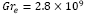, la velocidad máxima alcanzada para las curvas A4 y B4 en 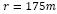y la curva C4 en /. 

Tabla 1 Velocidad máxima (m/s) alcanzada por el termal con la altura 

Fuente: Los autores.

La Fig. 5 se observa en un rango muy pequeño de distancia Δz como la velocidad máxima en el termal, para seguidamente comenzar a disminuir como evidencia en las curvas A3, B3 y C3, dando cuenta de la gran magnitud de las fuerzas que están implicadas en el caso representado en la Fig. 5. Los resultados obtenidos muestran como la velocidad máxima que alcanza la partícula de fluido moviéndose a lo largo del eje z depende de las dimensiones del termal, es decir, a medida que el termal tiene una altura máxima mayor (300, 600 y 900m), así mismo será mayor la velocidad máxima alcanzada por la partícula en comparación con otros termales con altura máxima menor como se evidencia en Figs. 3, 4 y 5 y la Tabla 1.

En la Fig. 6 la velocidad máxima alcanzada en la curvas A4 y B4 se dan a una misma distancia del eje del termal (radio r) aproximadamente de r =175m, en comparación con la curva C4 que se da aproximadamente a z = 145m. En la curva C4 se observa una simetría respecto al eje 𝑢 𝑟 , algo muy característico porque no se ve en los demás casos estudiados, se podría argüir que lo que está sucediendo en esta caso es que antes de alcanzar la velocidad máxima que sería aproximadamente de 4.5 m/s existe una preponderancia del esfuerzo normal que actúa sobre el termal, y que de la misma manera después del punto donde se alcanza la velocidad máxima existe esta misma prevalencia pero en este caso protagonizada por el esfuerzo viscoso comprometido en el fenómeno. 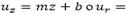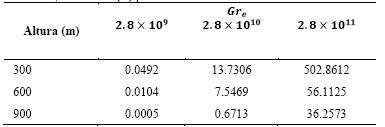En Tabla 1 se muestra la velocidad máxima alcanzada por el termal, y de este se puede concluir que antes de alcanzar la velocidad máxima la partícula de fluido tiende a comportarse de forma lineal ,es decir , se puede construir una función de la forma o de manera que se puede calcular el tiempo que la partícula de fluido se demora en alcanzar su velocidad máxima, este tiempo depende de la altura máxima del termal antes de detenerse y del número de Grashof efectivo /; a medida que la altura máxima del termal aumenta para un número particular, el tiempo que demora en alcanzar la partícula de fluido su velocidad máxima es menor , si se toma una altura en particular y se varía el número de Grashof (Gr) se tiene que el tiempo también disminuye. Como se indica en la Tabla 2.

Tabla 2 Tiempo adimensional que tarda un termal en alcanzar su velocidad máxima 

Fuente: Los autores.

A medida que la altura máxima del termal aumenta el número de Grashof aumenta dando cuenta de un crecimiento en la fuerza boyante que actúa sobre la partícula de fluido en comparación con el efecto viscoso sobre ella, en las Figs. 3, 4 y 5 para cada termal existe una velocidad máxima alcanzada y esta velocidad es mayor a medida que la altura máxima va creciendo; dado que la altura máxima del termal es directamente proporcional a la velocidad máxima del mismo esta proporcionalidad se puede explicar por el aumento en la fuerza boyante para cada caso, en donde el término boyante es del mismo orden que la magnitud de la aceleración vertical. Para las Figs. 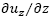3, 4 y 5 se pueden determinar el efecto del esfuerzo normal, e ₁ de la forma particular, de lo cual se tiene

(24)

Donde z₀ es la altura donde se alcanza la velocidad máxima y z _max es la altura máxima del termal. Los valores de las constantes A, B, C y D se muestran en la Tabla 3. En la Tabla 3 se ve como el esfuerzo normal antes del valor z₀ tiene un valor constante que ocasiona el aumento de la velocidad, de la misma forma después del punto 𝑧 0 el esfuerzo normal comienza a disminuir provocando la disminución de la velocidad. Una característica importante en el estudio de los termales como se muestra en las Figs. 3, 4 y 5 se basa en cómo estos alcanza su velocidad máxima a altura pequeñas en comparación con su máxima altura, en la Fig. 3 por ejemplo la velocidad máxima alcanzada para cada caso A1, B1 y C1 en 1/4, 1/2 y 1/75 de la altura del termal máxima, es decir, a medida que el termal tiene una altura máxima mayor este alcanza su velocidad máxima cada vez más cerca de su fuente, el precedente resultado se puede extender para las Figs. 4, 5, 6 y 7. Lo anterior, se puede interpretar tomando el punto de altura donde se alcanza la velocidad máxima como el punto donde los efectos viscosos son considerables en comparación con los efectos de cuerpo, bajo la suposición de que la velocidad ascensional media en el hongo es sustancialmente más pequeña que la velocidad en la columna del termal, Fig. 1; por tanto, la velocidad ascensional media en el hongo del termal, Fig. 1, en este modelo se asume igual a cero, (región que en este trabajo no es abordada) para la condición de contorno superior, es decir, la escala de tiempo de modelado es mucho menor que el tiempo que tarda en desarrollarse el hongo.

Tabla 3 Valor de las constantes A, B, C y D para el esfuerzo normal,e₂. Ecuación (24). 

Fuente: Los autores.

Fuente: Los autores

Figura 7 Velocidad de la partícula, 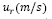del termal en función del radio del termal, r (m) para un número constante de 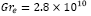, la velocidad máxima se alcanza para las curvas A5 y B5 en r = 50m y la curva C4 en r =8m. 

Para las Figs. 6, 7 y 8 se pueden determinar el efecto del esfuerzo normal, e₂de la forma particular, de lo cual se tiene

(25)

Donde r₀ es la altura donde se alcanza la velocidad máxima y r _max es la altura máxima del termal. Los valores de las constantes E, F, G y H se muestran en la Tabla 4

En el punto del termal cuando el radio es igual a cero se tiene la temperatura máxima que este puede alcanzar fijando un valor de altura, los resultados que muestran las Figs. 6, 7 y 8, afirman la relación inversa entre el radio del termal y la temperatura, por lo tanto las densidades de las partículas de fluido en la frontera del termal son las máximas, la anterior esta en concordancia con lo que nos muestra las Figs. 6, 7 y 8.

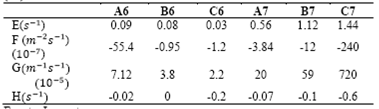
Tabla 4 Valor de las constantes E, F, G y H para el esfuerzo normal,e₂. Ecuación (25)  

Fuente: Los autores.

Fuente: Los autores.

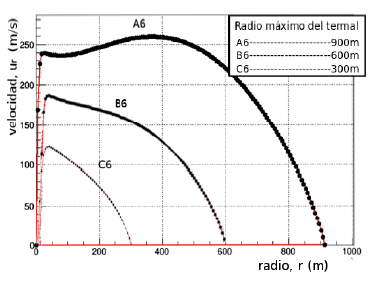
Figura 8 Velocidad de la partícula, del termal en función del radio del termal, r (m) para un número constante de.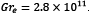 

Sucede en el caso mostrado por Figs. 6, 7 y 8 donde a medida que el número 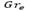aumenta la fuerza boyante permanece constante porque se estudia el flujo en un punto constante de altura y, en consecuencia, es el efecto viscoso el que cambia para cada caso. En las Figs. 6, 7 y 8 la velocidad es nula en los extremos, es decir, en los puntos de máximo radio en este caso la comparación con el esfuerzo normal y el efecto viscoso, antes de la velocidad máxima es el esfuerzo normal el que tiene mayor importancia en comparación con el efecto viscoso y, después de superar el valor r0 es el efecto viscoso el que tiene mayor preponderancia como la muestra la Tabla 4, en la cual el esfuerzo viscoso tiene un valor constante entes del valor 𝑟 0 dando cuenta de su mayor aporte y, finalmente, después del valor r0 el esfuerzo viscoso cae como se evidencia en la Tabla 4. En la Fig. 8 resaltan dos puntos en los cuales se ve una velocidad máxima, y tienen diferentes valores para cada curva. Para la Fig. 8 la curva A6 las velocidades máximas son en y de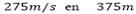, lo anterior puede dar cuenta de un esfuerzo radial que aparecen en el termal que puede actuar en un rango de radio determinado y después desaparecer, este esfuerzo actua justamente en los puntos donde se alcanzó un nuevo pico de velocidad máxima en 25m para A6. Para la curva C6 se da un comportamiento parecido al que muestra las curvas A5 y B5 de la Fig. 7. Se puede decir que la variación media de la densidad dada en la aproximación de Boussinesq se restringe a

(26)

la ecuación (26) muestra que las variaciones medias de la densidad del el fluido son despreciables en comparación con la densidad media del fluido, por tanto el aumento de la velocidad máxima de los termales con números de Grashof efectivos, 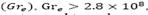se da por el aumento de la fuerza boyante en el termal.

El trabajo realizado por R.Woodward en 1959 [²¹] ha hecho visible el movimiento interior de un termal liberando pastillas blancas de 5 mm de diámetro en este, se garantizaba el equilibrio con trozos de alambre fino unidos a ellos por lo que tenían una muy pequeña velocidad terminal en el agua. A continuación, el termal estaba iluminado por un haz de luz plano de unos 3 cm de espesor, y el movimiento en la sección vertical central del termal fue fotografiado en 16 mm película de cine. Este experimento mostró cómo la velocidad en un termal es mayor en el centro que en sus extremos evidenciando un contraste diferente con un vórtice, dado que en un vórtice por lo general la velocidad aumenta al acercarse a los extremos, por ejemplo, vórtice rígido. En las Figs. 6, 7 y 8 se destaca el comportamiento descrito por R.Woodward para un vórtice, la velocidad del termal 𝑢 𝑟 en las gráficas aumenta del centro a sus extremos un comportamiento característico de un vórtice, este fenómeno se da hasta cierto punto en el termal porque después su velocidad comienza a disminuir como lo muestran las Figs. 6, 7 y 8 en concordancia con lo descrito por R.Woodward en su trabajo como características de un termal. La fuerza de boyamiento solo actúa verticalmente y es la que causa la aceleración del termal, en las Figs. 3, 4 y 5 el aumento de la velocidad se da hasta cierto punto causado por la fuerza boyante , después la velocidad disminuye hasta cero dado que la fuerza boyante no puede compensar el peso que ha adquirido el termal a medida que este va adquiriendo masa y aumentando su volumen; cabe destacar el papel que cumple en este fenómeno el esfuerzo viscoso entre las mismas partículas que hacen parte del termal y el esfuerzo viscosidad entre el termal y el medio que se mueve (por lo general el aire), el esfuerzo viscoso en este caso en cualquier parte del movimiento contribuye a la disminución de la velocidad del termal pero esta no es suficientemente grande para detener el aumento de la velocidad en el primer tramo del movimiento, es decir, antes de que el termal comience a reducir su velocidad drásticamente, en cambio cuando la velocidad comienza a disminuir la viscosidad no toma un papel importante dado que la tasa de cambio de la velocidad en función de la altura y el radio de las Figs. 3, 4, 5, 6, 7 y 8 no son mayores comparadas con las tasa de cambio antes de iniciar la disminución de la velocidad. El tiempo promedio para las distintas alturas, Tabla 2, con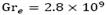 es de 3.2s, para 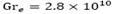es de 0.38s y para .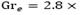

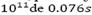Los resultados descrito por R.S. Scorer [⁵] muestran la forma como se comportan masas aisladas de líquido boyante que fueron liberados en un tanque de agua, lo cual mostro la forma como se relacionan la velocidad ur y r del termal:

(27)

donde B es la fuerza de boyamiento media, g la aceleración de la gravedad y C una constante, C = 2 determinada por R.S. Scorer [⁵]. R.S. Scorer concluye que las constantes tendrán el mismo valor tanto para los fenómenos atmosféricos como para las masas aisladas, esto se confirma más o menos por la observación de las torres de nubes de cúmulos. Algunas de las características del movimiento observado en los experimentos realizados en R.S. Scorer [⁵] se describen y la comparación se hace con los anillos de vórtice. Para calcular la fuerza de boyamiento media en un termal se utiliza la ecuación (27) de manera que se obtienen los siguientes resultados. Tabla 5.

La Tabla 5 muestra como al mantener constante el número de Grashof efectivo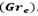, la fuerza de boyamiento disminuye a medida que aumenta la altura del termal. La razón del comportamiento descrito anteriormente está en que el volumen del termal al tener una altura más grande aumenta y su masa disminuye en comparación con los casos de menor altura, esto ocasiona que la fuerza disminuya por la disminución de la presión dado el aumento del volumen, y esto se evidencia en la disminución de la fuerza de boyamiento media. Como resultado de esta mezcla el volumen crece de forma continua y aunque el momento vertical aumenta de manera constante a través de la acción de la fuerza de boyamiento la velocidad disminuye a causa de la incorporación de fluido exterior. En los termales la Tabla 5 muestra como a medida que el número de Grashof (Gr) aumenta la fuerza de boyamiento también lo hace, un resultado que está acorde con la definición (14). Las Tablas 1 y 5 muestran cómo se puede caracterizar de forma eficiente el problema del termal utilizando el número adimensional de Grashof (Gr), de manera que cuando este número aumenta tanto la velocidad máxima (m/s) alcanzada por el termal como la fuerza de boyamiento media (N) para un termal aumentan y, más aún, se ve como la aceleración aumenta dada la fuerza de boyamiento según la Tabla 5.

Tabla 5 Fuerza boyante media (N) para un termal. 

Fuente: Los autores.

5. Conclusiones

Se implementó un modelo, desacoplado, en las coordenadas principales de un termal (altura, radio) que representan una ventaja respecto de las ecuaciones (11) y (12), por ser estas un sistema acoplado y no lineal, exigiendo un tiempo de compilado grande y gran complejidad algebraica para resolver el problema. La utilidad del modelo está en que brinda resultados útiles, con gran rendimiento de cómputo para recursos limitados, y mayor simplicidad algebraica. Esto se evidencia en el tiempo de compilación para los resultados mostrados en las Figs. 3, 4, 5, 6, 7 y 8 que promediaban entre 5 a 7min, tiempo que es muy inferior a otros cálculos para problemas similares que promedian las 10 a 15 horas. Por lo tanto el método computacional empleado funciono correctamente ya que mostro los resultados esperados, una de las dificultades es el aumento del tiempo de compilación al estudiar termales con alturas mayores a 900m. Este aumento es del orden del 90%. Con el estudio unidimensional del fenómeno de los termales se pueden extraer conclusiones claras sobre su cinemática y dinámica de manera que se puede modelar claramente este fenómeno. Se mostró la relación directa de uz y ur con el número de Grashof (14) de manera que la velocidad 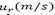del termal tiene dos factores que determinar su comportamiento la fuerza de boyamiento que disminuye a medida que aumenta la altura del termal, Tabla 5, y el esfuerzo normal el cual tiene un valor constante que ocasiona el aumento de la velocidad, despues del punto donde se alcanza la velocidad maxima el esfuerzo normal comienza a disminuir provocando la disminución de la velocidad como lo muestra la Tabla 3, de la misma manera 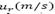tiene una relación importante con el esfuerzo normal equivalente a la dependencia mostrado por como se ve en la Tabla 4. De manera que el estudio anterior nos muestra de manera adecuada como pueden evolucionar muchos fenómenos relacionados con el ascenso de un fluido dentro de otro como por ejemplo: una columna de humo de un incendio en un pozo petrolero, una fuente hidrotermal, la cual consiste en un fisura en el fondo del océano y de la que se expulsa agua con mayor temperatura en comparación con el agua del océano.