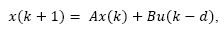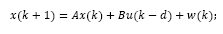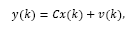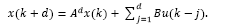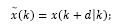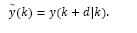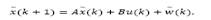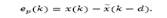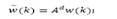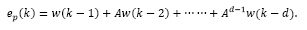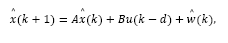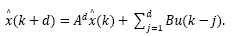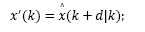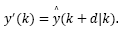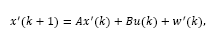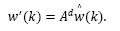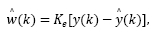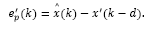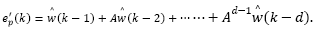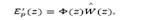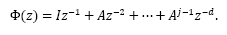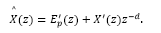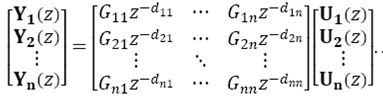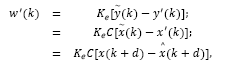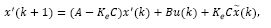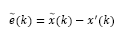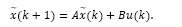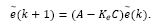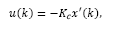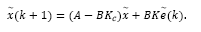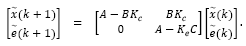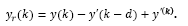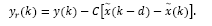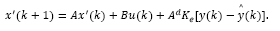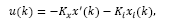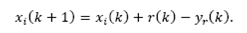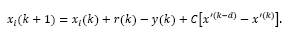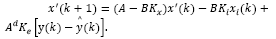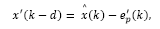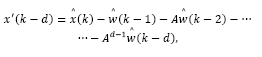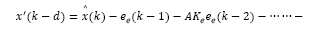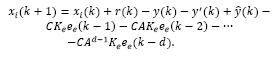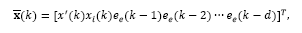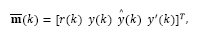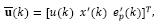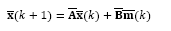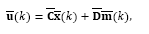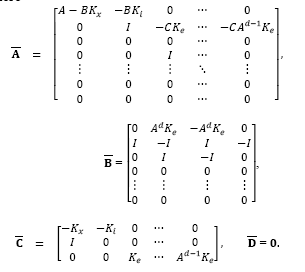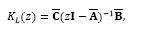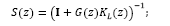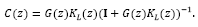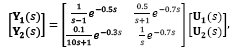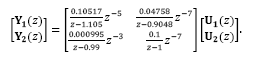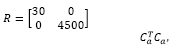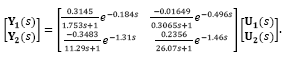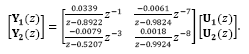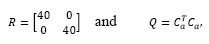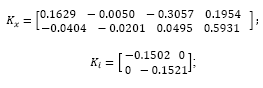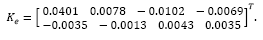1. Introduction
Dead-time systems, sometimes also referred to as transportation lag systems, can be found in many real processes. They are especially common for the chemical or biological plants, being also found in many industrial applications or communications. Mass and energy transportation or package losses in a network are just a few examples linked to this matter [1]. Control system complexity increases as dead time also does, as it is necessary to apply dead-time compensation techniques in this case [2].
Therefore, the closed-loop control of dead-time systems may exhibit an observer structure in order to compensate the dead time and avoid oscillations or even instability. Such observer is commonly referred to as predictor, while the Smith predictor is the first dead-time compensator reported in literature [3]. Basically dedicated to the representation of transfer functions, this structure and its respective variations have been used over the last decades to deal with plants that present dead-time. Some modifications include the Filtered Smith Predictor (FSP) [4,5]. A simplified version of the FSP has been proposed recently by [6] being able to deal with stable, integrative, and unstable first-order dead-time processes. A case study of dead-time compensation (DTC) in a second-order plus dead-time (SOPDT) system is reported in [7], where the Modified Smith Predictor (MSP) strategy is applied.
On the other hand, optimal control techniques are known by their robustness properties widely studied and well-established in literature. One of them is the LQG/LTR control [8,9], which has been initially proposed for continuous-time systems, while robustness conditions for the discrete-time case can be found in the work developed by [10]. Despite of its popularity few examples can be found in literature that link LQG for dead-time systems, e. g. [11,12]. Such approaches employ state augmentation to accommodate time delay, which increases computational effort, making them unattractive for implementation purposes.
However, a study of the DTC structure under the linear fractional transformation (LFT) framework with a loop shifting approach is presented in [13]. The extension of the loop shifting approach to the case of multiple delay systems was presented in [14]. Following the same approach, a solution to an equivalent delay-free H2 problem was proposed in [15].
Although the aforementioned approach deals with a dead-time compensator structure, it is developed for the continuous-time case, while this work is driven for the discrete-time case. Here we propose to modify the DTC structure presented by [16], in order to obtain a predictor-observer. Hence, one can apply any well-known and suitable technique to obtain both a state feedback control law and state estimation. Therefore, the proposed control structure obtained is applicable for linear dead-time systems, with the dead time explicitly compensated and the optimal control problem addressed for the linear model of the process without time delay. An advantage of this approach over traditional DTC is the fact that the same algorithm can be extended for MIMO systems. By using this approach, the best properties of both controller and predictor-observer are mixed resulting in improved performance in terms of robustness and step response. In addition, the proposed control scheme is applied to a classical linear MIMO plant case study to investigate its performance over multivariable case.
This paper is organized as follows. Problem statement is presented in section 2. Section 3 shows a review on the explicit dead-time compensation followed by its modification in order to get the predictor-observer structure. The separation principle in section 4 let us able to apply a state feedback control law for the predicted state, where the proposed control strategy with its block diagram is presented, followed by the robustness analysis in section 5. Simulation examples are present in section 6 and the implemented case for an incubator prototype is present in section 7. Conclusions in section 8 end the paper.
2. Problem statement
Consider the dead-time linear system whose model in discrete-time is given by:
where x(k) and u(k) are the state and input of the system, respectively, and d is the discrete time delay.
Many multivariable approaches for processes with model given by Eq (1) may be found under transfer function framework. One of those is the extension of the FSP for MIMO systems [17]. This approach has proved to be suitable for many well-known examples, despite of the inherent coupling between loops. The design procedure of the FSP algorithm considers to obtain a fast-model of the plant whose performance is improved if L i = min (L i j ) = L ii , i.e., when the minimal delay j in each row is the one in the main diagonal of the transfer matrix [1]. Although the aforementioned approach is applied for square systems, an extension of the MIMO-FSP for non-square system has been recently proposed [18], where a fast model without any time delay may be considered.
Under state space framework, state augmentation has been initially proposed to deal with dead-time, where an implicit representation, which may be found for instance in [19], is commonly reported [11, 16]. By this approach the order of the matrices of the system increase as dead-time also does. Therefore, systems with longer delays lead inevitably to high dimension matrices. From the computational effort viewpoint this is an undesirable condition, as operations may be critical for embedded systems
In order to overcome this issue, some approaches have been proposed where dead-time is compensated by matrices with the same order as those of the plant. One of these is based on the internal model control (IMC) proposed by [20], where the Generalized Multi-Delay Compensator (GMDC) [21] is split in two parts: a fast model and a delayed one. By this approach, the primary controller is designed for an undelayed plant and a reference filter may be required. The derived control schema is able to control MIMO plants.
Solutions based on predictor approaches have been recently proposed as in [16], although the multiple delay case considers the augmented representation. The case of multiple dead-times has been considered for SISO systems in [22,23]. In order to deal with time-varying delay Gonzalez et al. [24] proposed a predictor-based controller with stability analyzed under LMI framework, applied for SISO systems. Under this perspective, this work is intended to present a predictor-based approach that avoid the use of augmented state to ease implementation. The proposed control method is able to deal with both SISO and MIMO square plants with multiple dead-times.
3. State estimation and prediction
Classical representations of dead-time systems include state augmentation. However, this approach increases the order of the model, which may lead to lengthy matrices. In order to avoid high order matrices to represent the dead time, an explicit dead-time compensation structure is used by [16] and analyzed in terms of robust stability. Such structure is called a predictor as the development therein explicitly provides state estimation d steps ahead from the measurements instant.
3.1. Explicit dead-time compensation: A review
In order to apply the explicit dead-time compensation structure under the optimal control framework, this section provides a brief review on the predictor aforementioned. Such predictor was proposed in the work by Santos et al. [16], so that this section is intended to give a brief review.
Consider a dead-time system with state disturbance and input delay whose discrete-time model is given by:
where d is the time delay, x(k), y(k) and u(k) are the process state, output and input, respectively. It is assumed that the pair (A,B) is controllable and (A,C) is observable. Also, w(k) and v(k) are white noise additive disturbances related to the state and output, respectively.
Note that for a discrete-time system, the control signal u(k) affects state and output only at k + d time instant, i.e., x(k + d) and y(k + d). Then, by recursively applying eq. (1)d steps ahead, one gets an expression capable to predict the state of the system, given by:
It is important to mention that the expression defined in eq. (4) depends uniquely on the actual state x(k) and the past values of the control actions, so that it can be readily obtained. In addition, by considering v(k+d|k) as the variable v written d steps ahead, with information available up to time sample k, it is convenient to define:
Therefore, by considering eq.(5), the system described by eq.(2) may be written d steps ahead, leading to the predictor:
where w (k) is the effect of disturbance w (k)over x (k).
Predictor given by eq.(7) has to guarantee estimation for x(t) instead of x (k). Then, it has to be considered the prediction error defined as:
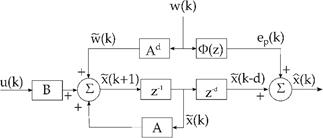
Fig. 1 shows the structure derived from eq. (7). As stated by Lemma 1 in [16], such predictor is input to state stable (ISS) if w(k) is bounded and u(k) is given by a feedback control law that stabilizes the delay-free model of the plant. For such condition, Santos et al. [16] have shown that:
Under optimal control framework it is usual to consider a state estimator. For the delayed system described by eq. (2), an estimator may be given by:
where 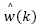 is an estimate of the state disturbance w(k).
is an estimate of the state disturbance w(k).
Likewise performed in the previous section, 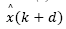 may be obtained by recursively applying eq. (11) dropping
may be obtained by recursively applying eq. (11) dropping 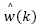 from it, which gives
from it, which gives
In this case it is suitable to define
Therefore, by applying eqs. (12)-(13) into the observer described by eq.(11), one gets the predictor-observer:
where 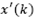 is the effect of the estimated disturbance
is the effect of the estimated disturbance 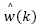 over the predicted-observed state
over the predicted-observed state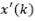 . In this case, eq. (9) becomes
. In this case, eq. (9) becomes
State disturbance w(k) in eq. (9) is defined under the invariant sets framework in [16] to obtain the structure in Fig. 1. On the other hand, under the optimal control perspective, this work proposes to consider
where  and
Ke
is the estimator gain which may be found by any technique, e. g., pole placement or optimal estimation error (Kalman filter). Note that such consideration already takes into account the fact that
and
Ke
is the estimator gain which may be found by any technique, e. g., pole placement or optimal estimation error (Kalman filter). Note that such consideration already takes into account the fact that 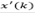 is bounded if the pair (A,C) of the delay-free system is observable and the poles of
A − Ke C
lie inside the unit circle. However,
is bounded if the pair (A,C) of the delay-free system is observable and the poles of
A − Ke C
lie inside the unit circle. However, 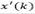 in the predictor-observer given by eq. (15) has to be bounded also. So that, we have to consider the prediction error, described by eq. (8), for the predictor-observer, which becomes:
in the predictor-observer given by eq. (15) has to be bounded also. So that, we have to consider the prediction error, described by eq. (8), for the predictor-observer, which becomes:
On the other hand, eq. (10) applied for the predictor-observer gives the prediction-estimation error:
In this case, eq. (15) defines the predictor whose structure is shown in Fig. 2.
It is important to highlight that according to eq. (19), this error depends uniquely on the past values of the estimated disturbance 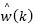 which can be written in the z-domain by
which can be written in the z-domain by
where
Therefore, by writing eq. (18) in the z-domain and replacing eqs. (20)-(20) into it, we have
Note that eq. (21) defines a FIR filter, which is always stable, whose entry is given by eq. (17) that is a bounded signal. Then, the term 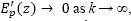 , which makes the convergence of the predicted state
, which makes the convergence of the predicted state 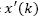 a fundamental issue.
a fundamental issue.
It worths to analyze the predictor-observer from the disturbance perspective. Then, by replacing eq. (17) into eq. (16) we have 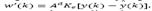 i.e., the effect of the estimation error over the predicted state
i.e., the effect of the estimation error over the predicted state 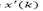 depends on the outputs of the system and the delay d. If a single time delay is considered, like for SISO systems, then no additional issues are related to obtain
depends on the outputs of the system and the delay d. If a single time delay is considered, like for SISO systems, then no additional issues are related to obtain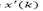 .
.
On the other hand, consider a nth -order square MIMO system with multiple dead-times given by the transfer matrix
In this case each output Yi (z), i=1,2,…, n is described by a linear combination of transfer functions Gij z−dij, i, j = 1,2,…,n . So that, the system we wish to control is described for the cases where i = j while i ≠ j describe transfer functions related to control actions of the others manipulated variables and can be seen as “disturbance” signals. Therefore, for the multivariable case, the predicted disturbance is given by
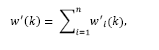
where
Focusing on eq. (23) one can notice that the proposed technique takes into account the actual delay of each output, i.e., there is no need to consider a fast model. Moreover, performance is improved if the maximum delay in each row is that in the main diagonal.
4. State estimation and the proposed control
The latter section presented an observer that combines the state estimation with its prediction, in order to compensate the time delay of a dead-time system. In this section we investigate the predictor properties, under the estimator viewpoint, and link it with the feedback control law.
4.1. State prediction-estimation
In order to compute the predicted state given by eq. (15), it is necessary to consider the predicted disturbance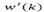 . As mentioned earlier,
. As mentioned earlier, 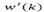 is the effect of the estimated disturbance
is the effect of the estimated disturbance 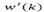 in the future state estimation.
in the future state estimation. 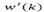 However, note that eq. (17) may also be applied for
However, note that eq. (17) may also be applied for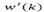 , as it holds in the time instant k + d as well. Then, one may write
, as it holds in the time instant k + d as well. Then, one may write
where x(k + d) and 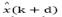 may be computed by eqs. (11)-(12), respectively. Then, by replacing eq. (24) into eq. (15), the predicted state is given by:
may be computed by eqs. (11)-(12), respectively. Then, by replacing eq. (24) into eq. (15), the predicted state is given by:
which is stable if the eigenvalues of
A − KeC
lie inside the unit circle. For such condition, the delay-free model pair matrices (A,C) must be observable. This is an important conclusion for the predictor-observer because if 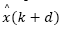 has guaranteed convergence, then so it has
has guaranteed convergence, then so it has 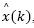 , according to eq. (22).
, according to eq. (22).
4.2. Control law
The problem of state estimation addressed in the later subsection shows that the variable 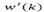 given by eq. (25) is an accurate prediction of the state of the system d steps ahead. Despite of that, a feedback control law cannot be applied if the future prediction error does not converge.
given by eq. (25) is an accurate prediction of the state of the system d steps ahead. Despite of that, a feedback control law cannot be applied if the future prediction error does not converge.
On the other hand, the system we wish to control is given by the predicted model:
Note that eq. (26) can be written as:
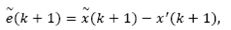
where replacement of eqs. (25) and (27) into it lead to
Then, by considering a feedback control law such as
the regulator case is applied to eq. (27), which allows us to write:
Thus, the closed loop is formed by eqs. (28) and (30), leading to
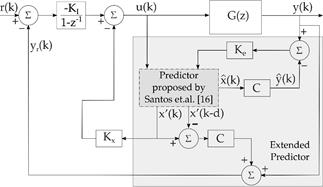
It is worthy to point out that the estimator gain in eq. (17) is applied to measurements taken at time instant k, while eq. (29) is a feedback law based on the future state estimator at k + d. However, eq. (31) shows that the Separation Principle holds for the predictor-observer structure of the Fig. 2, i. e., estimator and control poles may be assigned independently. Note from eq. (30) that the controlled system is stable if the eigenvalues of ( A − BKc ) lie inside the unit circle, i. e., if the pair (A,B) of the delay-free system is controllable. So that, feedback gain Kc in eq. (29) may be computed by any known method, e.g., pole-placement or optimal state feedback.
4.3 Closed-loop relationships
The predictor-observer in Fig. 2 may be viewed as a structure that provides an accurate state prediction 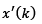 of the state estimation
of the state estimation 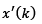 of the actual state x(k). In light of that, if the delay-free system is controllable, the application of the control law given by eq. (29) stabilizes the delayed system.
of the actual state x(k). In light of that, if the delay-free system is controllable, the application of the control law given by eq. (29) stabilizes the delayed system.
However, by paying attention at the traditional Smith Predictor (SP) structure shown in Fig. 3, it is noticed that the output of the system considered in the feedback path is given by
Taking this equation under the state space representation, one may write
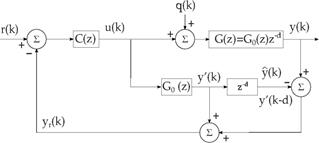
All the quantities in the right side of eq. (32) are available in the predictor described in subsection 3.2 as can be seen in Fig. 2. Then, for the purpose of reference tracking, the output feedback loop may be set as for the SP.
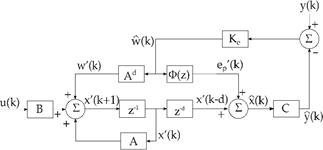
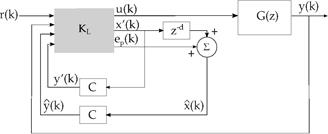
However, in order to obtain a block diagram for the proposed control method, by replacing eqs. (16)-(17) and eq. (29) into eq. (7), the predicted state is then given by:
For the tracking problem, the control signal is written as
where Kc=[Kx Ki] and xi (k) is the integrator state, written as
Replacing yr (k) given by eq. (32) into this equation, gives:
By replacing eq. (34) into eq. (33), the predicted state model becomes:
So that, the predicted state estimation and the output feedback given by eqs. (36) and (32), respectively, can be set into the block diagram shown in Fig. 4.
It is important to highlight that by this approach all the involved matrices to compensate the dead-time have the same order of that of the system model. Hence, digital implementation of such strategy is less affordable, from the computational burden viewpoint, than those based on state augmentation. Note that the algorithm derived from the structure in Fig. 4 is applied for both SISO and MIMO linear cases.
The proposed control method can be summarized as follows:
Compute gains Ke and Kc of the estimator and state feedback, respectively, for the delay-free system;
Split Kc = [Kx Ki];
Apply the gains previously computed into the diagram shown in Fig. 4.
5. Robustness analysis
Implementation of the control strategy as shown in Fig. 4 is a feasible task because the order of all the involved matrices is the same of those of the plant. However, for robustness analysis purposes, it is suitable to take the sensitivity and complementary sensitivity functions, which turns mandatory to obtain associated transfer functions, which are not immediate from Fig. 4.
Therefore, the analysis presented in this section is driven to obtain an equivalent state space representation of the diagram shown in Fig. 4, in order to obtain the sensitivity and complementary sensitivity functions. Within this context, from eq. (18) we have
where applying eq. (19) into it lead to
and considering eq. (17), one gets
where 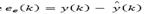 is the estimation error of the delay-free model.
is the estimation error of the delay-free model.
Thus, by replacing eq. (37) in eq. (35) the integral state is then given by
Therefore, by defining the augmented state
the input vector
and the control vector
then eqs. (36), (38) and (34) may be written in a single system in order to obtain an equivalent controller for the augmented state space model given by:
where
For robustness analysis purposes eqs. (39)-(40) may be written as
so that, one may readily find the sensitivity and complementary sensitivity functions [25]:
The equivalent structure of the proposed controller is shown in Fig. 5.
6. Simulation case study
The linear multivariable system considered in this section is a plant which exhibits stable, unstable and integrating modes. The plant has been previously studied in [20], whose transfer matrix is given by:
where Y1(s) and Y2(s) are the Laplace transform of the outputs y1(t) and y2(t) , respectively. This example is a very attractive multivariable plant because it includes integrating, unstable and stable transfer functions, as well as multiple dead-times. In addition, the minors dead-times are not all in the main diagonal, so that, this plant does not represent the more favorable dead-time system, which occurs when the minimal dead-time in each is the one presented in the main diagonal, as pointed out in [1]. In this case the control approach for MIMO systems proposed by [20] becomes a suitable control solution, successfully applied for this process.
The system in eq. (44) has been discretized considering a zero-order hold and the sampling time Ts = 0.1 s , with discrete-time representation:
In this case Y1(z) , Y2(z) , U1(z) and U2(z) are the Z-transform of the related time outputs and inputs.
The plant exhibits four states with two outputs, which means two additional states related to the integral action, i.e., six states to be fed back and four states to be estimated. In a case of a pole placement approach one gets 10 poles to be assigned. Hence, in order to reduce design effort it has been considered to apply optimal state feedback control law (solution to the associated LQR problem), which has been set with:
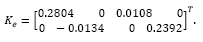
where R and Q are control and state matrices, respectively, and Ca = [C I] comes from the augmented model considered to include the integrator. State estimation applies a classical pole placement, which desired closed loop poles have been set to pdes = [0.9048 0.99 0.99 0.9]. Note that the poles in pdes are the stable poles of the model, however it replaces the unstable ones, z=1.105 and z=1, by the stable poles z=0.99 and z=0.9. Such tuning parameters lead to
and
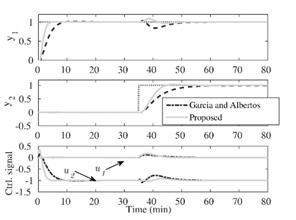
A step response simulation has been performed for both the proposed control method and the MIMO controller proposed by Garcia and Albertos [20], with tuning parameters therein. Results are shown in Fig. 6. The control method in [20] considers the design of a primary controller taken from a H-∞ problem, although a P/PID has been considered for this case. Additionally, a reference filter is included to avoid the undesirable effect of the zeros included by the controller. If a faster response is necessary the overall design has to be considered. Note that two transfer matrices have to be tuned: the reference filter and the primary controller. On the other hand, a faster or slower step response for the proposed controller can be achieved by simply modifying the main diagonal of the weighting matrix R. Decrease it for the former and increase it for the latter. Also, time response is considerably more decoupled (compare y1 outputs at about 40 min) which makes the tuning of the weights almost independent ( R11 for the output y1 and R22 for the output y2 ). So, tuning procedure is quite intuitive and simpler than that of the controller proposed by Garcia and Albertos [20].
7 Experimental case study
Previous section presented the effectiveness of the control method proposed in this work through examples that include SISO and MIMO dead-time systems. In this section the control strategy is implemented in an experimental system, consisting of a pilot plant of a Neonatal Incubator Care Unit (NICU). The main goal is to control both temperature and humidity of an inner dome what makes it an experimental MIMO set up. Such plant is attractive from the viewpoint of the control field because control of temperature and humidity is found in many industrial applications and a control strategy that works properly for the NICU system may be extended for other plants.
The arrangement is a prototype unit assembled at Electrical Engineering Department of the Federal University of Ceará with two main parts: data processing unit and incubator unit.
The data process unit consists of a desktop computer, where the code if the controller runs, and a Nidaq-USB6009 data acquisition card manufactured by National Instruments. Computer communicates through USB cable with the data acquisition card to manage analogue inputs and outputs to read data and apply voltage signals, accordingly.
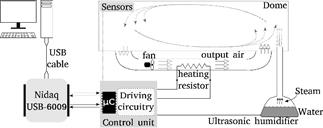
The incubator unit is a three stage equipment divided as follows. On top stage is a box-like acrylic made enclosed ambient, commonly referred to as dome, mounted over a plate with two main holes where the air flows in and out. The middle stage houses a heating resistor and a fan, for temperature control purposes. At the bottom one finds an ultrasonic humidifier which controls the inner humidity of the dome on top stage. Fig. 7 presents a picture of the incubator unit described above.
The temperature control works with a fan, that operates at constant speed, while the operation point of the heating resistor modify the inflow air temperature. For that, the power of such resistor is modified through a driving circuit whose command signal comes directly from the analogue output port of the Nidaq-USB6009 card. A similar connection is assembled for the ultrasonic humidifier, whose steam is driven through a separate tube for the dome. A schematic view of the incubator unit is shown in Fig. 8, with details as described above. Sensor readings are provided in digital words to a microcontroller which converts them to analogue voltage values, in order to allow connection with input port of the Nidaq-USB6009 card.
The plant has been identified by applying non-linear optimization with constraints to a set of step responses for both temperature and humidity loops. Those steps were performed with nothing inside the dome to emulate any thermal charge. Therefore, the results show the ability to control temperature and humidity inside an ambient as a room. The resulting linear model is given by:
All the time constants and dead-times are in minutes. The model given by eq. (49) has been discretized with Ts = 0.2 min with a zero order hold to obtain the discrete-time transfer matrix:
The process presents a significant interaction between both loops and multiple delays, as indicates eqs. (49) - (50). Such characteristics make it an attractive plant to apply MIMO control strategies as the one proposed in this work.
As performed for the MIMO example in section 6, we considered the associated LQR problem in order to find the optimal state feedback control law, which has been set with
where R and Q are control and state matrices, respectively, and Ca = [C I]. In this case, the estimator gain is not computed from the pole placement procedure, as it is considered the optimal estimation (Kalman filter) instead. Therefore, by applying the LQR problem together with the Kalman filter we consider the LQG approach as the primary controller. Robustness is improved by applying the well-established loop transfer recovery (LTR) [8, 9]. The LTR parameters are as follows: state covariance Rw = q2BBT, q = 1 and output covariance Rv = I, which lead to
and
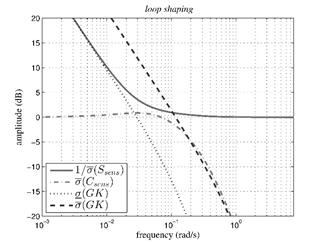
The tuning parameters were chosen in order to guarantee set-point to be tracked within 2% error in less than 30 minutes for humidity and 50 minutes for temperature. In addition, it is desirable maximum overshoot of 5% for humidity and no overshoot for temperature control loops. It is also usual to consider the trade-off between robustness and performance behavior. Related to this matter, the graphical design procedure named loop shaping is normally found for optimal controllers (see for instance [25,26]), whose graphs for this case study are shown in Fig. 9. This figure exhibits the graphs of the maximum singular value of the complementary sensitivity function 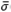 (Csens), the inverse of the maximum singular value of the sensitivity function 1/
(Csens), the inverse of the maximum singular value of the sensitivity function 1/ (Ssens) and the open loop GK maximum and minimum singular values,
(Ssens) and the open loop GK maximum and minimum singular values, 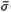 (GK) and σ(GK), respectively. The analysis is taken at the frequency range from ω = 10−3 rad/s up to ω = π/Ts rad/s, and it is desirable to keep
(GK) and σ(GK), respectively. The analysis is taken at the frequency range from ω = 10−3 rad/s up to ω = π/Ts rad/s, and it is desirable to keep 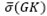 and σ(GK) within
and σ(GK) within 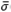 (Csens) and 1/
(Csens) and 1/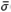 (Ssens) bounds for low and high frequencies, respectively [25].
(Ssens) bounds for low and high frequencies, respectively [25].
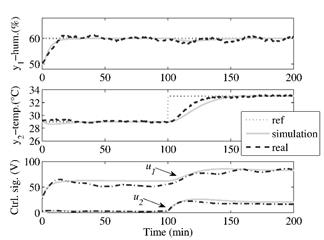
For this experiment, desired references have been set as 10% and 4°C above humidity and temperature of the room, respectively. Fig. 10 shows the step response for both simulation and real step response for a 200 min of total time. Note that the proposed controller successfully track references for both variables and guarantees the design specifications (settling time and overshoot, as mentioned earlier). Also, control signal related to both manipulated variables exhibits a smooth behavior, meaning that the additive noise is not fed back to the actuators.
8. Conclusions
This paper presents a control method which combines a predictor with a state observer, in order to compose a predictor-observer. The derived structure is able to predict the states of the system d steps ahead in order to compensate the dead time, so that, a state feedback control law can be obtained for the delay-free system. Simulation examples for SISO systems compare the proposed approach with SFSP recently proposed. For these simulations robustness graphs show the robustness improvement of the proposed method compared with the SFSP controller. A great advantage of the proposed control strategy is that it might be applied for both SISO and MIMO systems such that proposed structure does not have to be modified if the order of the model is. Additionally, the experimental MIMO system considered shows the practical aspect of the proposed controller.