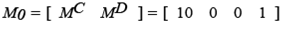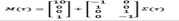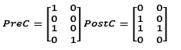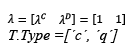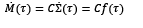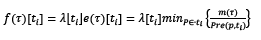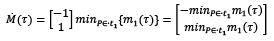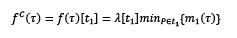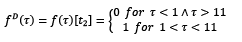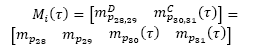1. Introduction
Tasks coordination in automated manufacturing systems can be designed by integrating subsystems characterized as purely Discrete Event System (DES) and others characterized as Hybrid Systems [2,7]. These automated systems should also consider unexpected abnormal situations monitoring some variables and triggering alarms when necessary. Due to these characteristics and requirements, the complexity involved in implementing a manufacturing automation system has increased and evolved from a simple direct application of the design specifications into the adoption of formalism-based methods.
An adequate formal method can ensure manufacturing automation systems efficiency, quality and safety characteristics [1].
DES modeling is largely used for designing production systems with good results [2-5], despite discrete behavior is in fact an approximation of the real behavior of these systems. In some cases, the continuous behavior of some variables has a great impact on general modeling and a hybrid system approach [6,7] is demanded. In such cases, the decision between adopting a full hybrid approach and trying to equalize continuous variables under a discrete modeling approach is not trivial. There are some practical advantages in the discrete approach, as for instance a suitable translation from the generated models, i.e., formal representations to control programs for industrial Programmable Logic Controllers (PLCs). Besides, in practice, a fully hybrid approach increases the complexity of systems analysis and implementation.
For instance, in construction industry [8] as well as in its associated infrastructure [9], there is a predominance of productive processes with discrete behavior; however, the control of variables such as speed and temperature affects the quality of the transport subsystem services and the manufacturing of building blocks, respectively.
Therefore, there are systems generally qualified as DESs that also include variables with a continuous behavior, which are very important in the control solution. In this context, a practical problem emerges which is to choose between the use of a fully hybrid approach or the fluidization of some parts [10] conserving the general DES modeling. Considering all the practical developments to implement automated manufacturing systems, especially using PLCs, the latter approach is more attractive. However, in this case, ensuring the reliability of the generated models (that will be converted in PLCs programs) is essential. A feasible solution is the introduction of hybrid concepts in specific parts of the discrete modeling approach [11,12], such as the hybrid extension of a Petri Net (PN) in the context of a technique called GHENeSys (General Hierarchical Enhanced Net System) [13], which follows the ISO/IEC 15909 standard.
Therefore, this paper proposes a formal method and the GHENeSys Timed Hybrid Petri Net (GTHPN) technique to design and to implement an automation system for the aforementioned cases. The GTHPN is based on timed and/or continuous PNs [2,11], and considers the fluidization concept through a subset of transitions and places under continuous firing at full time speed on infinite servers. In the proposed method, the system functional requirements are assessed based on the DES approach. Then, the fluidization concept is introduced to the modeling of the continuous parts, and the detailed behavior of continuous variables is gradually included, ensuring the integration of the different behaviors of the productive processes. GTHPN models can be converted in control programs into IEC 61131 languages for PLCs. A real industrial process of Manufacturing Concrete Building Blocks (MCBB) demonstrates the application and advantages of this proposal.
The theoretical aspects are discussed in Section 2. In Section 3, application cases are described. Section 4 describes the part of the proposed method for which a DES approach is adopted. Section 5 introduces the hybrid system approach. Section 6 presents the conclusions.
2. Petri nets and hybrid systems
Due to its power for analysis, synthesis and graphical representation, the PN is one of the most accepted formalisms to model DESs [2-5,10,14]. A place/transition (classical) PN allows modeling multiple productive processes and their behavior, such as sequence, concurrency, synchronism and parallelism. However, to improve the representation capacity of PN, several extensions have been proposed. A survey of related works involving some PN extensions (TPN [15], CIPN [16], IOPT PN [3], Controllable PN [17], Labeled PN [4], Timed Labeled PN [18], THPN [10], SHPN [19] and APN [20]) reveals techniques that properly combined would ensure the modeling of the global behavior of automation systems. However, there are works [16,5] that point to a gap related to methods that ensure a systematic application of control specifications, from its preliminary model direct to a PLC program.
GHENeSys [13], includes a hierarchical PN extention that follows the ISO/IEC 15909 standard and allows the development of control programs in IEC 61131 representation [21] for PLCs. Moreira el al. [16] present a survey that permits an analysis of the advantages of modeling a DES using GHENeSys [13] related to other PN extensions. Furthermore, Visual Object Net 2.7 (VON) software [22] can be used to model, analyze and simulate a GHENeSys net using arc enablers and inhibitors, and with auxiliary places (such as Controllable PN [17] uses) instead of labeled events (such as Labeled PN [4]). Control actions are transformed directly from the GHENeSys models to PLC programs. Even though this results in a solution that reduces the need of programming expertise, that proposal increases the effort necessary for modeling the system. The disadvantage of the GHENeSys-based method is related to the evaluation of dynamic behavior when continuous sub-systems are involved [2,14,23].
In [20], the APN-based approach is proposed, which associates external conditions to transition firing in the modeling of hybrid systems. This reduces graphical expressibility and needs additional firing rules, which increase the effort to generate programs for controllers. Therefore, the APN-based approach is more applicable to full hybrid systems different from the cases focused here.
Several formal approaches have been proposed for PN with continuous variables [2,11]. One of them, Timed Hybrid PN (THPN) [10], proposes the application of the fluidization concept to solve the firing of continuous transitions (for example, one transition can fire half of the firing time, later, another can fire three quarters, and so on). Thus, their firing counter and place markup are represented by continuous variables. Recent works [24,25] also presented some results using THPN-based methods; however, they do not consider the conversion or translation of the models into programs for industrial controllers.
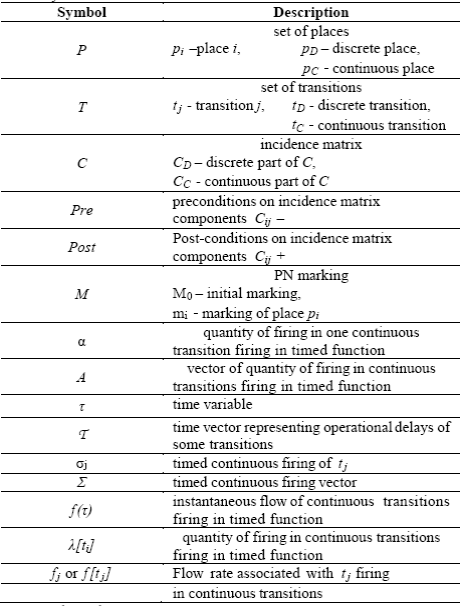
By definition (see Table 1) a system N with initial state M0 can be represented by a classical PN N=(P, T, Pre, Post), with marking M0(p) defined as a non-negative real for each p. The enabling degree of a continuous transition measures the maximum number of times a transition can be fired in one-step, and it is given by minp∈·t{mp/Pre[ p,t]}. The firing of t in a quantity α ≤ minp∈·t{mp/Pre[p,t]} carries a new marking M´= M + C[P, t]Α [23]. Thus, structural properties of a PN model for DES are transposed to a PN for continuous systems. However, the behavioral properties extension is not simple, because the firing of the transitions in PN for continuous systems can be done in relatively very small amount, so that a PN can be "almost" locked without ever stopping completely [10].
Different time constraints can be added to the firing of continuous transitions. One of them consists in associating an average speed to each transition. This approach becomes a continuous deterministic model, a system of nonlinear differential equations [10]. Let us consider that the marking has an overall continuous distributed variable system status; if there is an explicit time dependence in the state equation Mτ=M0+CΣ(σ(τ)) , where each σj(τ)≥0 , then, the equation representing the time evolution is obtained. Differentiating Mτ we have Cf(τ), in which f(τ) is the instantaneous flow of transition firing (i.e., fire per unit time) [23].
Commonly, the two semantics used in DES are finite or infinite server and both can also be applied to the continuous system. Each transition flow has an upper bound (the number of servers by the speed of each) under the finite server formal semantics (or constant velocity) [10]. If all the input places are marked for firing at the same speed, then the input places are limited by the flow to unmarked places. Under infinite server semantics or variable speed, the flow of a transition is the product of a constant (the server speed) by the enabling degree of the transition (number of active servers) [23]. That is:
In the finite and infinite servers semantic, the evolution of the system can be described as a set of switching linear equations. This change is not associated with an external event; it is the cause of the marking evolution. For finite server semantics, switching occurs when a place is empty. For infinite server semantics, switching occurs in synchronization when the input place is associated with minimum changes. For PN without synchronization, their behavior under infinite server semantics corresponds to a linear system [10]. Consider for instance the case of a transport subsystem, where a switch of speed allows synchronizing changes throughout the input of continuous places.
To allow a global view of the interaction among subsystems with different sequential processes, with either a discrete or continuous system behavior GHENeSys technique is extended to consider hybrid systems, throughout extensions based on concepts of the THPN technique. The P set must include discrete and continuous places, and the T set must include discrete and continuous transitions with continuous firing (at last one) based on infinite servers semantics, i.e., where the variable speed in the transitions depends of on input marking (servers) [26].
The GHENeSys is 7-tuple (L,T,F,K,M, Q, Π) in which: L is a set of distinct kinds of places: boxes (B) and pseudo-boxes (P) such that L=B∪P;. T is a set of activities; F is the flow relation F ⊆ (LxT ) ∪ (T xL) associated with connection arcs;. K is a mapping of L in the set natural numbers indicating maximum capacity of marks admitted in each place; M is the marking vector, related to the number of marks into each place; Q is a mapping that relates actions to some boxes subset or pulse or to some activities of transition firing; Π maps L and T elements to its corresponding hierarchical components. It assigns “0” value to simple places or transitions (B and T in normal-sized) and “1” to macro-elements (which are represented by larger-sized places).
The time associated with some transitions representing operational delays based on a pair (R,Τ) [2] can be used and associated to GHENeSys, such that: R is a marked GHENeSys; and Τ is a function which forms the set T of transitions to change (among positives and zero) the rational numbers. Thus, the transition tj has one time dj associated and when this transition becomes enabled, it is not fired immediately and will only be when the dj has elapsed after its enabling. All GHENeSys extensions (auxiliary places, small-sized pseudo-boxes, test and inhibitors arcs, and time associated to transitions) permit more expressive control conditions in dynamic behavior [13]. The hierarchy available by macro-places permits modular modeling avoiding states explosion which occurs in place/transition PN and more similarity in PLC programs (for more detail see [13]).
The GHENeSys THPN (GTHPN) is defined as 9- tuple (L, T , h, F, K, m, Q, Π, Τ) where: L is the set of places elements which include the boxes B and pseudo-boxes P sets. There are two types of B (discrete and continuous places: bD and bC, respectively). In BC , the number of marks are real positive numbers instead of being the positive integers as in BD ; T is the set of elements called activities in discrete and continuous transitions (tD and tC , respectively); h is called "hybrid function" and indicates whether each node is a discrete (bD and tD) or a continuous one (bC and tC), h: b{D,C} ∪ t{D,C}; F is the flow relation, F ⊆ (LxT ) ∪ (T xL), and these elements are called arcs (normal, inhibitor and test arcs); in the discrete case, (LxT ) ∪ (T xL) is a positive integer number and, in the continuous case, (LxT ) ∪ (T xL) is a positive rational number; K is the capacity function indicating maximum capacity of marks in each place B. M is the marking related with to the number of marks into each place (positive rational number in the continuous case or positive integer number in the discrete case). Q is a function that, in the discrete case, relates level actions (assign binary result) to some boxes subset or pulse (set or reset) to some activities or firing of transition. In the continuous case an analog IEC 61131 function is associated using Q function. Π is the function that defines the hierarchical types of L and T elements. It assigns "0" value to simple places or transitions (B and T in normal-sized) and "1" to macro-elements (which are represent by larger-sized places). Τ is a function from the set T of transitions to the set of positive or zero rational numbers: if tj ∈ tD, dj = Τ (tj) = timing associated with tj [2]; if tj ∈ tC, fj = 1/Τ(tj) = flow rate associated with tj.
The definition of a GTHPN is similar to the THPN [2,11,12], however, a GTHPN maintains the advantages of GHENeSys considering the transformation to binary and analogical IEC 61131 application models for automation systems.
3. Application case
The application case is the automation system of a transport subsystem of POYATOS Manufacturing Concrete Building Blocks (MCBB), located in Santiago de Cuba, Cuba [27]. This subsystem has great importance to the final product (concrete building blocks) quality because shocks or abrupt changes in transport carriage speed can affect the physical properties of the blocks.
The POYATOS MCBB can be divided into four sub- systems: dosage, pressing, transporting and packaging. After dosage and pressing, fresh blocks are put on the elevator. Once the elevator for the fresh blocks is filled, the transport starts. The carriage collects and moves the blocks on two rails into the curing cells, where these blocks are exposed to outdoor buffers, which have the same number of floors as the elevator. After the blocks are released from the outdoor buffers, they proceed to one of the adjacent dry blocks cells and are brought to the descended, which is responsible for going down the support boards, floor by floor, and placing the blocks in structures for packing.
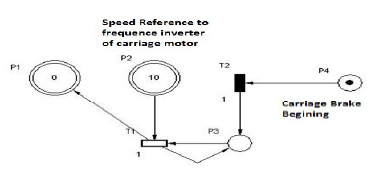
This carriage is mounted on a platform for transport. To make the carriage and the platform move on rails, the transport system uses two motors and mechanical speed reducers. This transportation can be performed at two speeds: slow and fast. Frequently, in successive attempts to ensure alignment, the motors are turned on and off for making small movements, which causes their deterioration and using severe displacements and, consequently, reduction of integrity and quality of the fresh blocks.
To ensure the flow of the processes in the transport subsystems as well as in other subsystems, a specified time schedule to conclude the tasks must be followed. If the transport subsystem presents delays, the entire productive system must be stopped. For example, delays of the transport carriage arrival have negative effects on productivity efficiency, and process quality. For that reason, an effective solution is needed linking the smooth precision movement with a minimal delay.
Despite the general process being approached as a DES, the fluidization technique must be applied to few parts. Therefore, a formal and detailed analysis of the process is performed. Initially, to ensure the correct operation of the transport subsystem, a requirement elicitation is made, considering the structural limitations.
The automated system for this MCBB is initially conceived based on a DES approach (non-hybrid; which is described in Section 4) to control the speed switching two values: slow speed (5m/s) and fast speed (10m/s). This non-hybrid approach reduces the manual operation problems, but keeps four abrupt velocity changes (0 → 5, 5→10, 10 → 5, and 5 → 0) which can affect the fresh blocks quality. Then, THPN modeling of continuous subsystems (hybrid; which is explained in Section 5) is conducted to assure a smooth and continuous increase at startup speed, and then a smooth and continuous decreased to stop. A minimal part of the continuous model must be defined to facilitate the translation of the models into IEC 61131 language.
The transport subsystem processes are divided into twelve steps, starting with the end of the actions performed, such as catch, transfer and download. There are seventeen position sensors: seven of them are limit switches activated when pressed, the other ten are inductive sensors activated when the metallic structures are closed. Therefore, to monitor system behavior and ensure efficient operation, metal tumblers were placed at required locations to detect the exact system positions.
4. Proposed method - Part I: Discrete event approach
Considering the structure and the requirements mentioned in the previous section, an initial discrete model is developed. The productive processes for concrete blocks transport at "POYATOS" manufacturing system are initially modeled in GHENeSys. Eighteen models are performed using the Visual Object Net 2.7 (VON) software [22]. The models correspond to the main control program, automatic system operation, emergency stop and 12 steps (except for the 4th and 7th steps which require two and three subnets, respectively), into which the automatic operation process was divided. This subdivision allows a modular approach that complies with the functional requirements considering the structural limitations and applying fluidization to only few parts when strictly required. For this, a particular analysis defines the minimal continuous parts, which are fundamental to increase the fresh blocks quality. This analysis is made using the available tools in VON software, which allows validating of the good properties of the GHENeSys models (see detail in [13]). In turn, these models describe the automatic operation (Subsection 4.1) and fresh blocks transport (Subsection 4.2).
4.1. Automatic operation
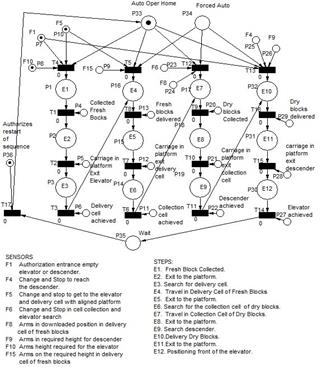
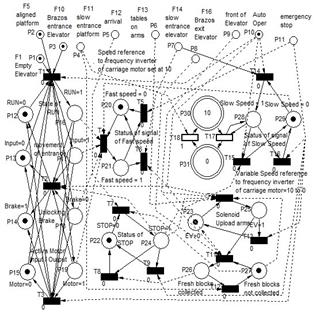
The automatic operation part of the process control is defined as a macro-place "Auto Oper" as shown in Fig. 1. This automatic function operates cyclically and can be activated by entering four different macro-places, which represent some steps of the block transport process, such as: "Fresh Block Collected" (E1), "Travel in Delivery Cell" (E4), "Travel in Collection Cell" (E7) and " Dry Block Delivery” (E10).
The reduction method [14] is selected to fulfill the analysis of PN properties such as limitability, reachability, firing, structural limitation and controllability. The underlying autonomous PN of the interpreted model is created and allows an analysis to solve conflicts, besides validating functional requirements, such as the inclusion of three re-starts represented by three macro-places of PN models in Fig.1 (E4, E7 and E10). These models contribute to increasing robustness in the control system for an emergency stop in an automatic and temporary way; i.e., the control system treats the failure for a certain time without restarting the system.
In this approach, the use of GHENeSys extended features, such as auxiliary places, differentiated arcs and macro-places, allow compatibility of the PN model with IEC 61131 [21] controller language, as explained in [12]. Macro-places modularity allows verification and validation of these models without the use of fluidization, because the analytic equations are included in some macro-places of Fig. 1. A case study is described in the following.
4.2. Fresh blocks transport
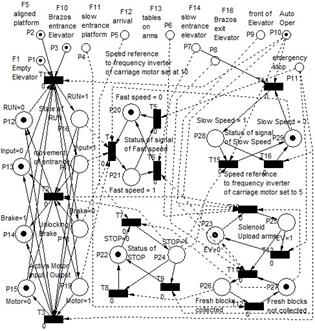
Speed variations cause shocks during transport, affecting fresh block quality. Thus, further details about the behavior of first step (E1) is necessary. As shown in Fig. 2, E1 operation depends on subsystem interactions and some process signal (auxiliary places in upper part) using extended arcs. Changes between Fast and Slow speed (P20-P21 and P28-P29) affect fresh block quality. It needed more attention.
Simplifying Fig. 2 to underlying autonomous PN model demonstrates that it comprises five separate sub models. The left side subnet is a simple synchronized PN that has all the initial places marked. For simplification, the other subnets are not presented here. However, two small upper subnets represent the activation and deactivation of the two possible speed values, places P28 (“active slow speed”) and P21 (“active fast speed”). Their translation into IEC 61131 programs correspond to the allocation of these reference values to PLC output, which adjusts the reference of the frequency converter of the main motor for the transport carriage (Fig. 3). The rest of the subnets are translated according to the translation rules defined in [13].
In this approach, the use of GHENeSys allows efficiency in the design of automation system according to IEC 61131 standard [21] using classical P/T nets. However, GHENeSys does not allow a smooth speed change in the transport carriage and does not guarantee the full quality of fresh blocks
5. Proposed method - Part II: Hybrid system approach
To apply a hybrid system approach to some parts of the speed control represented by E1 macro-place (see “Fresh Block Collection”) the GTHPN is used. It includes discrete and continuous places transitions. The continuous firing (at the last one transition) based on infinite servers semantics, i.e., variable speed in the transitions depending on input marking (servers) [26].
The advantages of discrete extensions (auxiliary places, different arcs, timed transitions and hierarchy by macro-places) are maintained. However, these advantages are increased according to the required application, including continuous testing in required subnets of the hybrid model. This allows a real representation of the environment using GTHPN to model E1 macro-place automatic operation for transporting fresh blocks at POYATOS.
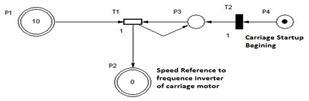
The model in Fig. 4 consider: 10 units for continuous charging times of P2 place (for increasing speed reference value at startup), 20 units for maintaining maximum speed (for maximum speed al constant movement) and 10 for continuous discharge of P2 place (for decreasing speed reference value during braking).
However, some steps do not require all smooth moving. For this reason, two independent PNs are developed to increase and decrease reference values for the carriage speed (see Figs. 5 and 8). For instance, at initial step 1, when the carriage picks up fresh blocks, it is not necessary to smooth the startup of the carriage because it is not loaded, but this control is necessary at the arrival (braking), which is close to the position where fresh blocks are located. The use of the SimHPN software [28] facilitated the theoretical and practical study of these models. Models only alter those parts that require moving fresh blocks, avoiding the need of a complete fluidization, as well as ensuring maximum simplicity in translation for IEC 61131-compatible programs. Even within parts that require speed control of the fresh blocks, just a fit must smoothly increase or must smoothly decrease through the independent PN that then are explained as follows.
Source: The authors.
Figure 4 Hybrid model for increasing or decreasing the speed reference value of the carriage represented by the P2 macro-place.
Source: The authors
Figure 5 Hybrid model of soft and continuous increasing of speed reference to transport fresh blocks in startup.
5.1. Start-up of transport carriage to fresh blocks
The edition of transport carriage PN in the SimHPN is performed using the pre and post-matrices of the equation state, the column vector of the initial marking M0 , the λ column vectors, and the T.Type which are the transitions firing speed and transition type, respectively.
All these elements are edited as show the lower and side windows of the SimHPN software of Figs. 6 and 7.
As a hybrid model, the marking M and incidence matrix C are partitioned into two sub-parts, continuous and discrete, without the combined part, because there is not one in this case. Therefore, for the initial marking:
Source: The authors.
Figure 6 SimHPN used to analysis of marking evolution of smooth continuous increase in transport carriage speed reference of fresh block during startup.

Source: The authors.
Figure 7 SimHPN used to analysis of flow evolution of smooth continuous increase in the transport carriage speed reference of fresh blocks during startup.
For this particular case, the fundamental equation becomes:
where the incidence matrix is composed of PreC and PostC matrices:
The firing of vector λ, representing the speed, is divided into two parts; the first is continuous for t 1 and the second is discrete for t 2. Eq. 5 shows the values in a vector and the types in the other:
The net dynamic behavior is given by the fundamental derived equation [29]:
Where:
For this case, the continuous sub-equation is as follows:
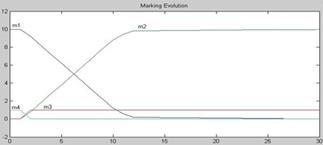
The elapsed time for each marking is given by Eq.8, as shown by Fig. 6. The P1 marking is decremented from 10 to 0 at a speed of one unit per second from τ 1 (1s) to τ 2 (11s); for P2, the behavior is the opposite. This includes exponential variations defined by “min” when P1 marking is smaller than 1.
The transition flows (which are presented in Fig. 7) are also subdivided:
The simulation obtained the marked behavior of each place and each transition flow (Figs. 6 and 7) of Fig. 5. This m 2 marking can be used as a reference for the speed controller of the transport carriage at start up. The P3 discrete marking limited to 1 defines constant t 1 flow equal to 1 with mark in P3. It creates a linear decrease in P1 marking (linear increase in P2). This is true until P1 marking is smaller than 1. When P1 marking force “min” value represented in Fig. 6 at final extremes of m 1 and m 2 graphs, its speed in the carriage with fresh blocks changes more softly from constant to stop, and constant to maximum. In this case, the behavior simulation of the proposed system after 11 seconds demonstrates that there is a small remnant flow of 0.3 units, slowly reduced to zero in 30 seconds. For that reason, the system implementation time is extended to 15 seconds to complete P2 charge and sets exactly the full carriage speed in soft start. If this does not occur, a jump would occur at the end of the high-speed motion. This dynamic simulation model demonstrates the soft start and stop control of fresh block transport.
Fig. 6 shows the switch of the marking of discrete places (m 3 and m 4) between 0 and 1 at time 1. At this point, the P2 load starts from 0 to 10 (at the same time as it begins downloading P1 from 10 to 0). This is the desired ascendant behavior for the speed reference at the carriage startup loaded with fresh blocks.
Fig. 7 shows continuous transition flow kept at its maximum value (1) while P3 place is enabled; the continuous marking of P1 place is greater than one, allowing obtaining limits and P-T semi-flows, but for such a simple net, this analysis is not required.
5.2. Braking the fresh block transport carriage
Fig. 8 represents the model for braking the fresh blocks transport carriage. In this example, if the charge and download are reversed from P1 to P2, the following command is reverse, i.e., from P2 to P1. In the same way as for increasing the model, the decreasing behavior of the carriage speed can be studied.
Similar behavior of marking and flow evolution of Fig. 5 PN is developed in Fig. 8 PN evolution, only in reverse conditions. It was tested in SimHPN.
5.3. Smooth decrease in speed reference of the motor inverter in step 1
Following, work sequences of the steps that require the starting and stopping operations are incorporated. Fig. 9 shows how a decreasing model is inserted into the operation sequence of the step 1 model. P30 place corresponds to a variable reference for decreasing the carriage braking (when P28 place - slow speed), which is activated enabling the t 17 continuous transition, with soft braking when the carriage arrives for loading fresh blocks. The t 18 continuous transition can also be provided to initialize the continuous execution at the end of step E1. The auxiliary places representing conditional system operation are removed from the model in Fig. 9; the autonomous model can be obtained from this PN model showing the functional and behavioral properties more clearly.
Source: The authors.
Figure 8 Hybrid model of soft and continuous decrease of speed reference to transport fresh blocks when braking
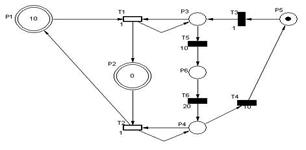
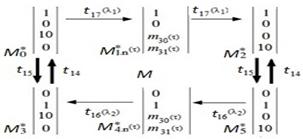
The autonomous model of hybrid subnet in Fig. 9 (up-right subnet) corresponds exactly to the model presented in [2]. Only one redundant transition t 16 (of t 15) is added, which can be removed and be fully compliant with the analysis properties. The interpreted PNs are also considered to disable the firing of t 16 transition with the P4 auxiliary place. The resulting reachability graph has status changes in one direction, defined by t 17 and t 18, and there are only fires of discrete transitions in maxim continuous marking (in m 30 or m 31 = 10) for the controlled system as shown in Fig. 10.
The marking vector is also considered:
For the controlled case, maximum speeds of timed continuous transitions are unitary (λ 1 = λ 2 = 1) and operate alternately, and never simultaneously.
Source: The authors
Figure 9 The hybrid model of step E1 with sudden rise but continuous and smooth decrease of the speed reference of the transport carriage of fresh block during braking
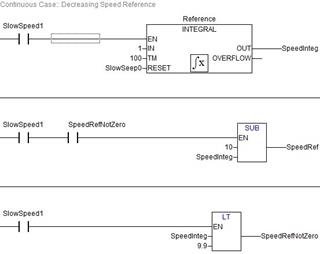
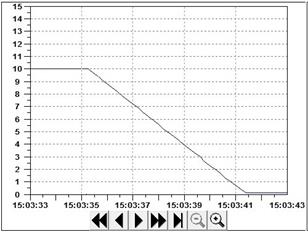
The reachability graph shows the controlled model and its liveliness behavior, and ensures the validation of the functional requirements of this formal analysis. Fig. 11 illustrates the translation of this continuous part into IEC 61131 language (ladder diagram). The Q function of GTHPN allows the association of IEC61131 function blocks (Fig. 11) to continuous part (P30-P31 of Fig 9) of the model in translation procedure. The specific IEC61131 function block is related to particularities of specific process control. This is the relevant contribution of GTHPN technique to IEC61131 compatibility of hybrid PN models. The analogy between the dynamic behavior of the model (Fig. 6) and the simulation results of the control program execution (Fig. 12) are almost corresponding, demonstrating the facilities of using GTHPN to model the reference carriage speed.
Based on GTHPN, the control solution is developed in modular form and assures compatibility between the model and the IEC61131 language. Similarly, a model for decreasing speed in step 1 was inserted. In the remaining steps, insertion is performed taking into consideration whether fresh blocks are directly affected. According to the analysis, only steps E1 to E4 require the use of hybrid approach models for smoothing the load movement with fresh blocks. This modification in the automation system of POYATOS MCBB is a significant advancement achieved in the quality production of building blocks.
Source: The authors adapted of [2]
Figure 10 Reachability graph of model of step 1. ( M i ∗ - hybrid macro-marking [2])
Source: The authors
Figure 12 Simulation of the control program execution of Speed Reference in the transport system
This example confirms that GTHPN allows modeling of the continuous behavior of the carriage speed variation within the discrete operation sequence, which ensures a more agile and efficient programming at the implementation phase of the project. The GTHPN models can be transformed into control programs for PLCs in IEC 61131 language, and the resulting program assures a required smooth and continuous behavior to decrease and to increase the speed in fresh building blocks transport guaranteeing full quality of the final products.
6. Conclusions
This paper proposes a method based on the GHENeSys Timed Hybrid Petri Net (GTHPN) to model automation systems in a gradual and modular approach. Specifically, the method fits discrete event systems in which some specific hybrid components have an important influence on the full general behavior. System functional requirements are initially conceived into modules adopting a discrete event approach, in which certain macro-elements (exploring the properties of GTHPN) are modeled. Then, specific variables that require continuous control are introduced into subnets of these macro-elements adopting the concepts of hybrid systems approach. Furthermore, a resulting GTHPN models can easily be transformed into programs of industrial controllers.
In the GTHPN Petri net extensions (auxiliary places, different arcs, timed transitions and hierarchy by macro-places) were combined with elements for continuous systems to fire transitions based on infinite servers semantics. In other words, the modeling hybrid system with GTHPN, which uses a GHENeSys-based method, extends the theoretical definitions of THPN.