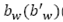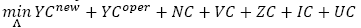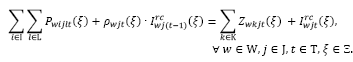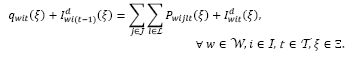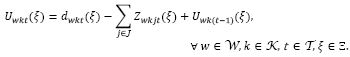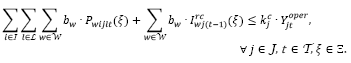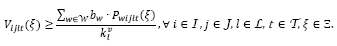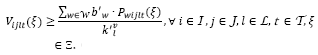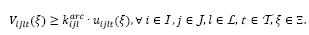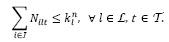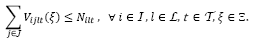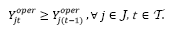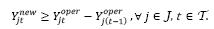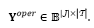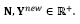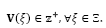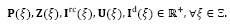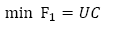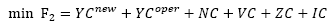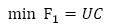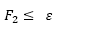1. Introducción
Las consecuencias de los desastres, naturales o causados por el hombre, en los últimos años han evidenciado la complejidad de esos eventos. En los últimos 30 años, por ejemplo, más de 17,360 desastres han ocurrido en el mundo, dejando más de 3 millones de víctimas fatales, miles de millones de afectados y millones de dólares en daños económicos [1]. Aproximadamente el 20.98% de esos desastres corresponden a inundaciones o movimientos de masas (avalanchas, flujo de detritos, deslizamiento de tierra y piedras), desastres que son de frecuente acontecimiento en muchos países. Debido a la complejidad inherente a ese tipo de eventos, en muchos casos los órganos encargados de la gestión de desastres no están preparados para responder de forma eficiente ante ellos, como se ha evidenciado, por ejemplo, en desastres como el de la región Serrana de Rio de Janeiro en Brasil [2] y en inundaciones frecuentes en muchas regiones de Colombia [3]. La imprevisibilidad del desastre y de su impacto dificulta más la toma de decisiones para mitigar el sufrimiento de las víctimas. Con recursos limitados, los órganos que realizan la gestión de desastres deben responder a cualesquiera que sean sus consecuencias, lo que sugiere la necesidad del desarrollo de herramientas que consideren las incertezas inherentes a ese tipo de eventos.
El ciclo de vida de las operaciones humanitarias está vinculado a la temporalidad de ese tipo de eventos. Existen decisiones/operaciones pre-desastre realizadas antes de la ocurrencia del desastre y decisiones/operaciones pos-desastre realizadas después del inicio del desastre. Entre esas decisiones, la coordinación de las decisiones de localización y distribución componen una importante área de estudio en logística humanitaria, pues en situaciones de desastre no existe un tradeoff claro entre localización y transporte en términos del costo total de la red. Además de eso, pocos investigadores se han preocupado en integrar el dimensionamiento de flota a las decisiones de localización y distribución. Por un lado, sobreestimar el número y los tipos de vehículos necesarios para realizar el transporte incurre en costos excesivos e, consecuentemente, en la escasez de recursos que podrían ser empleados en otras actividades. Por otro lado, subestimar la flota de vehículos puede causar una distribución ineficiente de los productos, una vez que los vehículos contratados no sean suficientes para la distribución.
La programación estocástica de dos etapas surge como una manera “natural” para modelar y resolver problemas en logística humanitaria, sobre la motivación de que las etapas pueden ser relacionadas al ciclo de vida de los desastres [4]. La primera etapa puede ser vista como la fase de preparación (pre-desastre) y la segundo etapa como la fase de respuesta al desastre (pos-desastre).
La definición de los objetivos en los modelos de gestión de desastres es una de las principales diferencias entre la logística humanitaria y la logística comercial. En ambos casos es común usar tanto modelos mono-objetivos como modelos multi-objetivos. Entre los objetivos más utilizados en logística humanitaria se destacan la minimización de los costos logísticos (costos de localización, contratación de vehículos, transporte, inventarios) y la minimización de la demanda insatisfecha (atraso) [5]. Esos objetivos son casi siempre contradictorios. Por un lado, minimizar la demanda insatisfecha implica en el aumento del flujo de productos y consecuentemente en el aumento de los costos logísticos. Por otro lado, los costos logísticos pueden ser minimizados al disminuir el atendimiento a las áreas afectadas, lo que aumenta la penalidad por demanda insatisfecha. Incluso siendo objetivos contradictorios, es común ver en la literatura modelos que mezclan esos dos tipos de costos en una misma función objetivo, dando una penalidad mayor a la demanda insatisfecha en comparación a los costos logísticos.
En este artículo es desarrollado un modelo biobjetivo para el problema integrado de localización, distribución y dimensionamiento de flota en contextos multi-periodo, multi-producto y con flota heterogénea. El modelo considera un objetivo de costos logísticos y un objetivo humanitario. El modelo biobjetivo es comparado con una versión mono-objetivo del mismo. Son realizados experimentos computacionales con instancias generadas a partir de datos reales del megadesastre de la Región Serrana del Rio de Janeiro en 2011.
Lo que sigue de este artículo está organizado de la siguiente manera: la Sección 2 presenta la revisión bibliográfica; la Sección 3 describe el problema y desarrolla los modelos matemáticos; la Sección 4 discute los resultados computacionales; la Sección 5 presenta las consideraciones finales.
2. Revisión bibliográfica
Para una revisión más profunda sobre la evolución de la aplicación de técnicas y modelos matemáticos en el campo de la logística humanitaria los lectores pueden ver [6-11]. En los trabajos revisados, fueron identificados modelos aplicados principalmente a 5 decisiones en la gestión de desastres: localización de instalaciones, transporte de productos, dimensionamiento de flota, pre-posicionamiento de inventarios y evacuación de víctimas.
Algunos autores propusieron modelos de programación estocástica de dos etapas que consideran el pre-posicionamiento de inventarios en la primera etapa, en cuanto que la distribución de productos es realizada en la segunda etapa [12,13]. Adicionalmente, algunos autores integraron la decisión de evacuación de víctimas en la segunda etapa [14]. Es común también encontrar trabajos que integraron la localización y pre- posicionamiento de inventarios en la primera etapa y la distribución de productos en la segunda etapa [15-22]. Apenas 5 de los trabajos revisados [4,23-26] consideran las decisiones de localización, distribución y dimensionamiento de forma integrada. Algunos de esos trabajos consideraron en la primera etapa la localización de instalaciones y en la segunda etapa el transporte de productos y dimensionamiento de la flota [4,23,25,26]. Bataglin y Alem [24], por otro lado, consideraron en la primera etapa la localización y dimensionamiento de la flota y, en la segunda etapa, el transporte de productos. Salmerón et al. [23] adicionaron al problema de distribución de productos el rescate/evacuación de heridos en la segunda etapa.
De los trabajos revisados, dos trabajos [17,24] consideraron contextos multi-periodo, de los cuales apenas Bataglin y Alem [24] consideraron contextos multi-periodo, multi-producto y flota de vehículos heterogénea de forma simultánea. Claramente, existe un gap en el estudio de modelos de programación estocástica multi-periodos que integren localización, distribución y dimensionamiento de la fruta.
Entre los objetivos más utilizados en la literatura está la minimización del costo de transporte y de la demanda insatisfecha. Entre los objetivos menos utilizados está el costo de contratación de vehículos, considerados en apenas 2 trabajos [24,26]. Pocos de los modelos de programación estocástica revisados son multi-objetivo [18,23,26]. Además de eso, ningún de los trabajos se preocupó en realizar una comparación entre formulaciones mono-objetivo y biobjetivo de los modelos, siendo que, ambas son comúnmente utilizadas para modelar las operaciones en situaciones de desastres.
3. Descripción del problema
El problema presentado en este artículo combina los subproblemas de localización de centros de auxilio, transporte de productos, dimensionamiento de la flota y asignación de la demanda a los centros de auxilio.
3.1. Problema de localización
El problema de localización determina en cuál de las posibles localidades deben funcionar los centros de auxilio, considerando que la demanda debe ser atendida por los centros de auxilio abiertos. Pueden existir inventarios de productos en los centros de auxilio, siendo que no toda la cantidad de productos almacenados permanecen en condiciones de ser utilizados de un periodo para el otro debido al impacto del desastre. Los centros de auxilio abiertos deben permanecer en funcionamiento hasta el final de las operaciones humanitarias.
3.2. Problema de dimensionamiento
El problema de dimensionamiento de la flota consiste en la decisión de determinar las cantidades y tipos de vehículos que deben ser contratados en cada depósito para distribuir los productos para los centros de auxilio. Los vehículos son contratados por periodo, y su contratación no implica que sean realmente utilizados en el transporte de productos.
3.3. Problema de transporte
El problema de transporte de productos consiste en determinar la cantidad de cada tipo de producto que debe ser transportada de los depósitos hasta los centros de auxilio. Además, se debe determinar en qué vehículos (respetando las capacidades en volumen y peso) debe ser realizado el transporte de esos productos, considerando que existen un conjunto de rutas que, como resultado del impacto del desastre, no están disponibles para algunos vehículos.
3.4. Problemas de asignación
El problema de asignación de la demanda consiste en designar una fracción de la demanda de cada área afectada a cada centro de auxilio, donde las víctimas recibirán los ítems que necesitan.
3.5. Tratamiento de las incertezas
Conforme mencionado anteriormente, un desastre es un evento cuyas dimensiones son imprevisibles. En el problema tratado en el presente artículo son asumidos los siguientes parámetros como aleatorios: la cantidad de productos disponibles (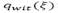 ) en los depósitos, que es resultado de donaciones o apoyo del gobierno; la proporción de inventario utilizable(
) en los depósitos, que es resultado de donaciones o apoyo del gobierno; la proporción de inventario utilizable(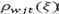 ) en los centros de auxilio, que depende de las condiciones de almacenamiento; la demanda (
) en los centros de auxilio, que depende de las condiciones de almacenamiento; la demanda (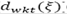 ) en las áreas afectadas, que depende del impacto del desastre sobre la población; y la disponibilidad de las rutas (
) en las áreas afectadas, que depende del impacto del desastre sobre la población; y la disponibilidad de las rutas (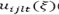 ), que depende de las consecuencias del desastre sobre la red de transporte. Es asumido que las variables aleatorias pueden ser bien aproximadas por un conjunto discreto y finito de escenarios
), que depende de las consecuencias del desastre sobre la red de transporte. Es asumido que las variables aleatorias pueden ser bien aproximadas por un conjunto discreto y finito de escenarios  , con probabilidades de ocurrencia
, con probabilidades de ocurrencia 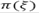 que designan la posibilidad de que tal escenario ocurra. A continuación se presentan los modelos mono-objetivo y biobjetivo del problema integrado de localización, distribución y dimensionamiento de flota.
que designan la posibilidad de que tal escenario ocurra. A continuación se presentan los modelos mono-objetivo y biobjetivo del problema integrado de localización, distribución y dimensionamiento de flota.
3.6. Modelo mono-objetivo
Conjuntos
W Productos requeridos por las personas afectadas.
I Depósitos desde donde salen las ayudas humanitarias.
J Centros de auxilio que reciben la ayuda humanitaria
K Áreas afectadas representadas por ciudades o regiones.
L Tipos de vehículos que pueden ser contratados.
T Periodos de tiempo de las operaciones humanitarias.
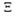 Escenario de ocurrencia de las variables aleatorias.
Escenario de ocurrencia de las variables aleatorias.
Parámetros determinísticos
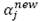 Costo fijo por apertura del centro de auxilio j (infraestrutura básica para las operaciones).
Costo fijo por apertura del centro de auxilio j (infraestrutura básica para las operaciones).
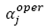 Costo fijo por operación del centro de auxilio j (energía, agua, grupo de ayuda humanitaria).
Costo fijo por operación del centro de auxilio j (energía, agua, grupo de ayuda humanitaria).
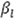 Costo fijo por vehículo tipo j comprar, contratar o mantenimiento).
Costo fijo por vehículo tipo j comprar, contratar o mantenimiento).
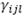 Costo de transporte del vehículo l en la ruta
Costo de transporte del vehículo l en la ruta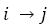 .
.
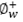 Costo de inventario del producto w.
Costo de inventario del producto w.
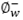 Penalidad por demanda insatisfecha del producto w.
Penalidad por demanda insatisfecha del producto w.
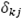 Costo del centro de auxilio j atender demanda del área afectada.
Costo del centro de auxilio j atender demanda del área afectada.
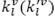 Capacidad en volumen (peso) del vehículo l.
Capacidad en volumen (peso) del vehículo l.
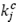 Capacidad total del centro de auxilio j (volumen).
Capacidad total del centro de auxilio j (volumen).
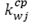 Capacidad de almacenamiento del producto w en el centro de auxilio j (cantidad de productos).
Capacidad de almacenamiento del producto w en el centro de auxilio j (cantidad de productos).
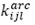 Número máximo de vehículos l que pueden atravesar la ruta
Número máximo de vehículos l que pueden atravesar la ruta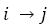 .
.
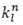 Número máximo de vehículos l disponibles para las operaciones humanitarias.
Número máximo de vehículos l disponibles para las operaciones humanitarias.
Parámetros estocásticos
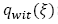 Suministros del producto 𝑤 al depósito i en el periodo t en el escenario ξ.
Suministros del producto 𝑤 al depósito i en el periodo t en el escenario ξ.
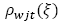 Proporción del producto 𝑤 en el centro de auxilio j en el escenario ξ que permanece utilizable entre dos periodos t - 1 y t.
Proporción del producto 𝑤 en el centro de auxilio j en el escenario ξ que permanece utilizable entre dos periodos t - 1 y t.
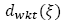 Demanda del producto 𝑤 en el área afectada k en el periodo t en el escenario ξ.
Demanda del producto 𝑤 en el área afectada k en el periodo t en el escenario ξ.
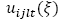 = 1, Si la ruta
= 1, Si la ruta 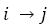 está disponible para el vehículo l en el periodo 𝑡 en el escenario ξ.
está disponible para el vehículo l en el periodo 𝑡 en el escenario ξ.
= 0, en caso contrario.
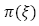 Probabilidad de ocurrencia del escenario ξ.
Probabilidad de ocurrencia del escenario ξ.
Variables de decisión de primera etapa
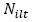 Número de vehículos l designados al depósito 𝑖 en el periodo t.
Número de vehículos l designados al depósito 𝑖 en el periodo t.
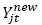 = 1, si el centro de auxilio j abre en el periodo .
= 1, si el centro de auxilio j abre en el periodo .
= 0, en caso contrario.
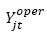 = 1, si el centro de auxilio j opera en el periodo
= 1, si el centro de auxilio j opera en el periodo
= 0, en caso contrario.
Variables de decisión de segunda etapa
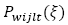 Cantidad del producto 𝑤 transportado en la ruta
Cantidad del producto 𝑤 transportado en la ruta 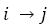 por el vehículo l en el periodo t en el escenario ξ.
por el vehículo l en el periodo t en el escenario ξ.
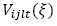 Número de veículos usados en la ruta
Número de veículos usados en la ruta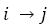 en el periodo t en el escenario 𝜉.
en el periodo t en el escenario 𝜉.
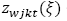 Cuantidad del producto 𝑤 en el centro de auxilio j para atender demanda del área afectada 𝑘 en el periodo 𝑡 en el escenario ξ.
Cuantidad del producto 𝑤 en el centro de auxilio j para atender demanda del área afectada 𝑘 en el periodo 𝑡 en el escenario ξ.
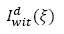 Inventario del producto 𝑤 en el depósito i en el periodo t en el escenario ξ.
Inventario del producto 𝑤 en el depósito i en el periodo t en el escenario ξ.
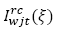 Inventario del producto 𝑤 en el centro de auxilio j en el periodo 𝑡 en el escenario ξ.
Inventario del producto 𝑤 en el centro de auxilio j en el periodo 𝑡 en el escenario ξ.
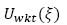 Demanda insatisfecha del producto 𝑤 en el área afectada k en el periodo 𝑡 en el escenario ξ.
Demanda insatisfecha del producto 𝑤 en el área afectada k en el periodo 𝑡 en el escenario ξ.
Sea Λ el conjunto de todas las variables de decisión. El modelo de programación estocástica de dos etapas para el problema de localización-distribución de productos con dimensionamiento de flota es formulado de la siguiente forma:
Función objetivo:
en que
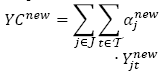 es el costo total de apertura de los centros de auxilio;
es el costo total de apertura de los centros de auxilio;
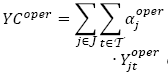 es el costo total de operación de los centros de auxilio;
es el costo total de operación de los centros de auxilio;
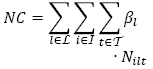 es el costo total por designación (contratación) de los vehículos;
es el costo total por designación (contratación) de los vehículos;
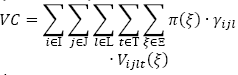 es el costo total de transporte;
es el costo total de transporte;
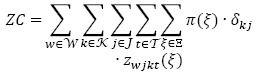 es el Costo total de atendimiento de las áreas afectadas:
es el Costo total de atendimiento de las áreas afectadas:
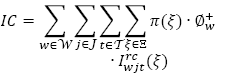 es el costo total de inventario en los centros de auxilio;
es el costo total de inventario en los centros de auxilio;
 es la penalidad total por demanda insatisfecha.
es la penalidad total por demanda insatisfecha.
Sujeto a las siguientes restricciones:
La función objetivo (1) minimiza el costo total esperado, compuesto por los costos de la primera etapa (apertura y operación de los centros de auxilio y designación de vehículos) y por los costos de la segunda etapa (transporte, inventario, atraso y atendimiento de la demanda). Las restricciones (2) y (3) garantizan la conservación del flujo de productos en los centros de auxilio y en los depósitos, respectivamente. En la restricción (2), el inventario que puede ser utilizado de un periodo para el siguiente es disminuido por la proporción de inventario utilizable 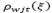 . La restricción (4) determina la demanda insatisfecha en las áreas afectadas. Sin pérdida de generalidad, es asumido que los inventarios y atrasos iniciales son nulos. Las restricciones (5) y (6) garantizan que no puede existir transporte en una ruta
. La restricción (4) determina la demanda insatisfecha en las áreas afectadas. Sin pérdida de generalidad, es asumido que los inventarios y atrasos iniciales son nulos. Las restricciones (5) y (6) garantizan que no puede existir transporte en una ruta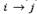 si el centro de auxilio 𝑗 no está en operación y limitan el flujo de productos de acuerdo con la capacidad total y por producto de los centros de auxilio. Las restricciones (7) y (8) determinan el número mínimo de vehículos necesarios para realizar el transporte de productos desde los depósitos hasta los centros de auxilio en la segunda etapa, respetando las capacidades (peso y volumen) de los vehículos. La restricción (9) garantiza que el vehículo 𝑙 solo puede recorrer la ruta
si el centro de auxilio 𝑗 no está en operación y limitan el flujo de productos de acuerdo con la capacidad total y por producto de los centros de auxilio. Las restricciones (7) y (8) determinan el número mínimo de vehículos necesarios para realizar el transporte de productos desde los depósitos hasta los centros de auxilio en la segunda etapa, respetando las capacidades (peso y volumen) de los vehículos. La restricción (9) garantiza que el vehículo 𝑙 solo puede recorrer la ruta 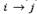 en el periodo 𝑡 en el escenario ξ si la ruta está disponible, i.e.,
en el periodo 𝑡 en el escenario ξ si la ruta está disponible, i.e., 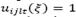 . Está restricción también limita el número de vehículos que pueden ser utilizados a la capacidad de transporte en la ruta
. Está restricción también limita el número de vehículos que pueden ser utilizados a la capacidad de transporte en la ruta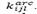 . La restricción (10) restringe el número de vehículos de cada tipo que pueden ser contratados por periodo en la primera etapa. La restricción (11) asegura que solamente los vehículos contratados en la primera etapa pueden hacer transporte en la segunda etapa. La restricción (12) garantiza que los centros de auxilio abiertos deben permanecer en operación hasta el final de las operaciones humanitarias. La restricción (13) asocia las variables de decisión de apertura a aquellas referentes a la operación de los centros. Las restricciones (14)-(17) representan el dominio de las variables de decisión.
. La restricción (10) restringe el número de vehículos de cada tipo que pueden ser contratados por periodo en la primera etapa. La restricción (11) asegura que solamente los vehículos contratados en la primera etapa pueden hacer transporte en la segunda etapa. La restricción (12) garantiza que los centros de auxilio abiertos deben permanecer en operación hasta el final de las operaciones humanitarias. La restricción (13) asocia las variables de decisión de apertura a aquellas referentes a la operación de los centros. Las restricciones (14)-(17) representan el dominio de las variables de decisión.
3.7. Modelo biobjetivo
En la función objetivo (1) pueden ser identificados dos objetivos: el objetivo humanitario y el objetivo financiero. El objetivo humanitario (F1) considera la minimización de la penalidad por demanda insatisfecha (o atraso), y el objetivo financiero (F2) consiste en la minimización de los costos logísticos. Esos dos objetivos son mostrados la seguir:
En el contexto de logística humanitaria varios métodos de optimización multi-objetivo han sido aplicados con éxito [26-30]. Se destacan entre ellos la optimización jerárquica (hierarchical optimization), la programación por metas (goal programming) y el método épsilon-restricción (epsilon constraint method). Técnicas heurísticas y meta-heurísticas son también comunes para tratar optimización multi-objetivo [31]. En la optimización jerárquica [32] es definido un orden de prioridad (jerarquía) para las funciones objetivo y el modelo es resuelto considerando apenas la función objetivo de mayor prioridad. Después de eso, el valor óptimo del objetivo prioritario es convertido en una restricción y el modelo es resuelto considerando apenas la función objetivo siguiente de mayor prioridad. Eso es realizado secuencialmente hasta considerar todos los objetivos. La programación por metas [33] difiere de la optimización jerárquica pues, como el su nombre sugiere, considera metas a ser alcanzadas para cada una de las funciones objetivo y penaliza el desvió entre los objetivos y las metas establecidas. El método épsilon-restricción [34], consiste en optimizar uno de los objetivos y considerar los demás objetivos en forma de restricciones adicionales.
De acuerdo con resultados obtenidos en experimentos computacionales preliminares fue escogido el método épsilon-restricción para resolver el presente modelo biobjetivo. Con el método épsilon-restricción fueron obtenidas más soluciones no dominadas que con los otros dos métodos para instancias similares. Además de eso, o método épsilon-restricción, que considera como una restricción el objetivo de costos logísticos, ofrece soluciones que pueden ser más fácilmente analizadas desde el punto de vista práctico. Esto porque el parámetro ε puede ser considerado como un límite para la cantidad de dinero disponible (presupuesto) para realizar las operaciones humanitarias. La formulación matemática biobjetivo del problema integrado de localización, distribución y dimensionamiento de la flota, de acuerdo con el método épsilon-restricción es presentada de la siguiente forma:
Sujeto a: Restricciones (2)-(17)
en que ε es un parámetro que indica el limitante superior considerado para el objetivo F2. Observe que alterando el parámetro ε pueden ser obtenidas diferentes soluciones para los objetivos (F1, F2) en el método épsilon-restricción.
El método épsilon-restricción, que considera como restricción el objetivo de costos logísticos, ofrece soluciones que pueden ser fácilmente analizadas desde el punto de vista práctico, pues el parámetro ε funciona como un limitante de la cantidad de dinero disponible (presupuesto) para realizar las operaciones humanitarias y la optimización biobjetivo permite analizar el impacto del aumento del presupuesto en el atendimiento a las víctimas del desastre. En este estudio no es utilizado el método épsilon-restricción para encontrar el conjunto de todas las soluciones no dominadas (conjunto Pareto óptimo) y si para encontrar un conjunto de soluciones que permitan analizar el comportamiento del atraso cuando son realizadas modificaciones en la cantidad de dinero disponible para llevar a cabo las operaciones humanitarias. El número de soluciones proporcionadas por el método épsilon-restricción depende de las variaciones realizadas en el parámetro ε, pueden ser generadas tantas soluciones como requeridas por los tomadores de decisión.
4. Experimentos computacionales
Los modelos fueron implementados en el software GAMS 24.1.3 (GAMS Development Corp.) y resueltos con el solver CPLEX 12.5.1 en un computador con 16 GB de memoria RAM, procesador Intel Core i7 y sistema operacional Windows 7. Fue establecido como criterio de parada un límite de tiempo de 3,600 segundos o un GAP de 1% de optimalidad. Los parámetros default del solver CPLEX fueron alterados, desligando los planos de corte, utilizando el algoritmo dual simplex y aumentando la frecuencia de utilización de la heurística RINS, de acuerdo con la mejor configuración encontrada en Moreno et al. [35].
Los datos utilizados fueron generados con base en datos reales del megadesastre de la región Serrana de Rio de Janeiro en 2011 [36,37]. Inicialmente, fue generada una instancia (M1). La instancia M1 considera 3 depósitos, 20 centros de auxilio, 5 ciudades afectadas, 5 tipos de productos (agua, alimentos, kit médicos, kit de higiene doméstica, kit de higiene personal), 3 tipos de vehículos (camiones, barcos y helicópteros), 5 escenarios (emergencia, crisis, menor, moderado, mayor) y 10 periodos. A partir de esa instancia, fueron construidas 7 instancias modificando algunos parámetros con el objetivo de analizar el comportamiento del modelo ante diversas situaciones. Fueron exploradas situaciones en que la cantidad de productos que llegan a los depósitos es alta (M2), la disponibilidad de los vehículos es baja (M3), uno de los tipos de vehículos no está disponible (M4), la capacidad de los centros de auxilio es reducida (M5), la capacidad de los vehículos es reducida (M6), el costo de apertura de los centros de auxilio aumenta (M7) y la cantidad de productos disponibles y la demanda disminuyen (M8). El conjunto de escenarios y las características de los productos y de los vehículos fueron establecidas de acuerdo con la literatura [35,38-41]. Para más información sobre las instancias utilizadas entrar en contacto con los autores.
4.1. Resultados computacionales
En el método Épsilon-restricción fueron obtenidas N =51 soluciones factibles variando el parámetro ε en el intervalo 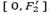 , en que
, en que 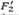 indica el valor del objetivo F2 cuando F1 = F1* (valor óptimo de F1), i.e., el costo logístico F2 alcanzado al resolver el modelo minimizando apenas la penalidad por demanda insatisfecha F1. El algoritmo Épsilon-restricción utilizado para encontrar soluciones del modelo biobjetivo es mostrado a continuación:
indica el valor del objetivo F2 cuando F1 = F1* (valor óptimo de F1), i.e., el costo logístico F2 alcanzado al resolver el modelo minimizando apenas la penalidad por demanda insatisfecha F1. El algoritmo Épsilon-restricción utilizado para encontrar soluciones del modelo biobjetivo es mostrado a continuación:
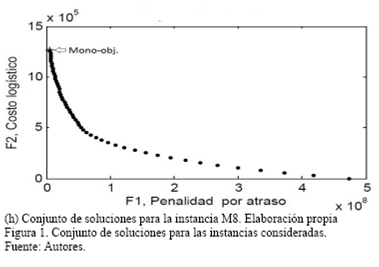
En la Fig. 1 es presentado el conjunto de soluciones obtenidas para cada una de las instancias (M1-M8). En la Figura, el eje horizontal representa la penalidad por demanda insatisfecha y el eje vertical representa los costos logísticos. El asterisco (*) y la flecha indican la solución del modelo mono-objetivo para esa instancia.
Como era esperado, es posible observar que al aumentar el presupuesto disponible para costos logísticos disminuye la penalidad por demanda insatisfecha. Note que aunque el costo logístico aumenta de forma constante (de acuerdo con el parámetro Δ) la penalidad por demanda insatisfecha no sufre una disminución constante. La disminución en la penalidad por demanda insatisfecha es menor a medida que el presupuesto es más alto, de hecho, para algunas instancias existe un punto en el cual la disminución de la penalidad comienza a ser casi imperceptible.
En relación a la solución mono-objetivo son observados dos comportamientos que dependen de los costos logísticos de cada instancia. Para algunas instancias con costos logísticos más altos (M1 con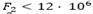 , M5 con
, M5 con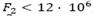 , M6 con
, M6 con 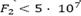 , M7 con
, M7 con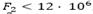 ) la solución mono-objetivo se encuentra entre los puntos entre los cuales la disminución de la penalidad por demanda insatisfecha se torna casi que insignificante a medida que aumentan los costos logísticos de forma constante. A partir de esos puntos, el aumento en los costos logísticos es mayor que la disminución de la penalidad por la demanda insatisfecha y, por tanto, no existe una ganancia significativa en la función mono-objetivo al aumentar los costos. Para otras instancias (M2 con
) la solución mono-objetivo se encuentra entre los puntos entre los cuales la disminución de la penalidad por demanda insatisfecha se torna casi que insignificante a medida que aumentan los costos logísticos de forma constante. A partir de esos puntos, el aumento en los costos logísticos es mayor que la disminución de la penalidad por la demanda insatisfecha y, por tanto, no existe una ganancia significativa en la función mono-objetivo al aumentar los costos. Para otras instancias (M2 con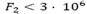 , M3 con
, M3 con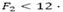
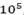 , M4 con
, M4 con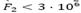 , M9 con
, M9 con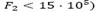 la solución mono-objetivo está entre las soluciones que presentan la más baja penalidad por demanda insatisfecha. En esas instancias, dado que los costos logísticos son menores, casi siempre el aumento en los costos logísticos implica una disminución mayor en la penalidad por demanda insatisfecha y, por tanto, existe una ganancia significativa en la función mono-objetivo al aumentar esos costos hasta alcanzar una penalidad próxima o igual a la menor posible.
la solución mono-objetivo está entre las soluciones que presentan la más baja penalidad por demanda insatisfecha. En esas instancias, dado que los costos logísticos son menores, casi siempre el aumento en los costos logísticos implica una disminución mayor en la penalidad por demanda insatisfecha y, por tanto, existe una ganancia significativa en la función mono-objetivo al aumentar esos costos hasta alcanzar una penalidad próxima o igual a la menor posible.
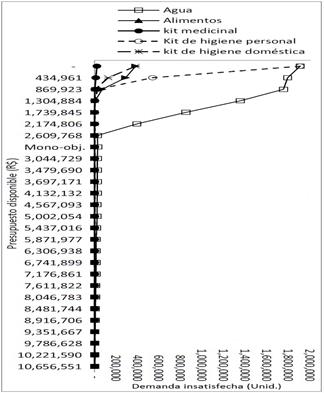
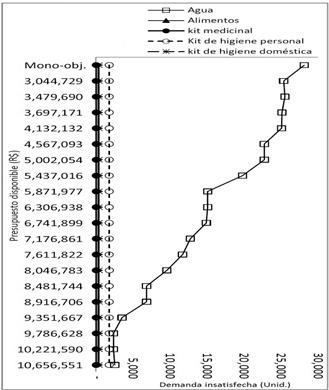
Para las instancias M2, M3, M4 y M9 el modelo biobjetivo presenta soluciones que son, desde punto de vista del nivel de servicio, tan buenas como las soluciones del modelo mono-objetivo. Por otro lado, para las instancias M1, M5, M6 y M7 el modelo biobjetivo presenta soluciones que mejoran el atendimiento a las víctimas de la solución del modelo mono-objetivo. Aunque esa mejoría en el atendimiento a las víctimas no sea significativa, pues la penalidad por demanda insatisfecha disminuye poco en relación al costo logístico, en el contexto práctico esa disminución en la penalidad puede significar el atendimiento de millares de víctimas, como pode ser observado en la Fig. 2. La Fig. 2 presenta el atraso de productos para cada uno de los niveles de presupuesto definidos en la optimización biobjetivo. Note que, de acuerdo con la Fig. 2, hasta el punto de la solución mono-objetivo (Mono-obj.) la disminución en la cantidad de productos atrasados es significativa. A partir de ese punto, “aparentemente” no existe ganancia en el atendimiento de la demanda. Pero, de acuerdo con la Fig. 3, en que es presentado el atraso de productos a partir de la solución mono-objetivo (Mono-obj.) de la instancia M1, se nota que existe de hecho una ganancia significativa en la entrega del producto agua. El atraso pasa de aproximadamente 28,000 unidades con la solución mono-objetivo para menos de 3,000 unidades en algunas soluciones no dominadas de la optimización biobjetivo. Un comportamiento similar fue observado en las demás instancias.
En los gráficos es posible observar que a medida que aumenta el presupuesto disponible para costos logísticos se prioriza la entrega de productos de menor volumen y mayor penalidad. De esa forma, el atraso de productos con una penalidad alta y volumen relativamente bajo (como medicamentos y kits de higiene personal) disminuye de una forma más acelerada que productos con menor penalidad a medida que aumenta el presupuesto. Eso explica el hecho de la disminución de la penalidad por demanda insatisfecha no sea constante a medida que aumentan los costos logísticos, pues inicialmente son distribuidos productos con mayor penalidad y menor volumen y después productos de menor penalidad y mayor volumen.
Fuente Autores
Figura 3 Atraso de productos en la instancia M1 a partir de la solución mono-objetivo.
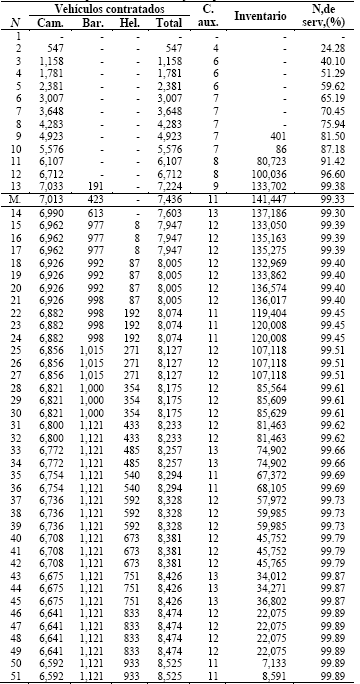
La Tabla 1 presenta el valor de los dos objetivos considerados, costo logístico (costo) y penalidad por demanda insatisfecha (penalidad), para diferentes niveles de presupuesto en la optimización biobjetivo de la instancia M1. La Tabla 2 presenta el resultado del número de vehículos contratados de cada tipo (camiones, barcos, helicópteros), el número de centros de auxilio abiertos (c. aux.), el número de productos almacenados y el nivel de servicio (N. de serv.) para los diferentes niveles de presupuesto en la optimización biobjetivo de la instancia M1.
Básicamente el comportamiento de las decisiones de contratación de vehículos, apertura de centros de auxilio y almacenamiento de productos fue similar en todas las instancias. Como era esperado, el número total de vehículos contratados, el número de centros de auxilio abiertos y el nivel de servicio aumentan a medida que existe mayor presupuesto disponible para costos logísticos. Los vehículos más utilizados son los camiones, pues son los que presentan un mejor trade-off entre costo y capacidad. Cuando el presupuesto es bajo, solo son utilizados camiones para realizar la distribución de productos. A medida que el presupuesto aumenta, vehículos como barcos y helicópteros son contratados para el atendimiento de rutas que no pueden ser atravesadas por los camiones. En algunos casos, además de eso, los helicópteros y barcos sustituyen los camiones en algunas rutas, por tanto, se observa una tendencia a la disminución en el número de camiones contratados cuando vehículos como barcos y helicópteros comienzan a ser utilizados.
Tabla 1 Resultados de la optimización multi-objetivo para instancia M1. Elaboración propia
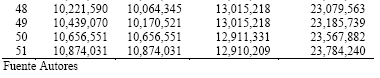
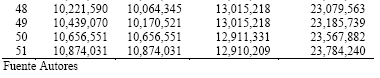
Fuente Autores
Para la mayoría de las instancias el inventario de productos es nulo cuando existe un presupuesto bajo, pues en esas situaciones el número de vehículos disponibles es apenas suficiente para realizar la distribución de la demanda de un periodo. A medida que el presupuesto aumenta más vehículos son contratados y es posible transportar, además de los productos que deben ser utilizados en el periodo, productos para dejar en inventario para los periodos siguientes. Así, el inventario comienza a aumentar, principalmente con el objetivo de aprovechar toda la capacidad de los vehículos disponibles.
Finalmente, cuando el presupuesto es alto, es suficiente y no es una preocupación por la disponibilidad de vehículos (pues existe dinero para contratar cualquier número de vehículos), la tendencia es a una disminución en los productos almacenados, pues el transporte no está preocupado por la consolidación para disminuir costos, sino por el nivel de servicio. En estos casos, aprovechar al máximo la capacidad de los vehículos no es más una prioridad y el inventario de productos es realizado apenas con el objetivo de cubrir la falta de productos en periodos futuros. Desde el punto de vista del atendimiento a las víctimas es preferible no almacenar productos si no es necesario, principalmente en situaciones en las que la cantidad de productos disponibles son limitados (recordando que parte de los productos almacenados quedan inutilizables de un periodo para el siguiente). En instancias en que la disponibilidad de los productos es mucho mayor que la demanda (instancia M2) no existe una limitación apretada de los productos, por tanto, la pérdida de productos en los inventarios no es tan relevante y el inventario de productos aumenta de forma continúa al aumentar el presupuesto disponible. El nivel de servicio, de forma similar al comportamiento de la penalidad por demanda insatisfecha, sufre cambios menores a medida que aumenta el presupuesto para costos logísticos.
En la instancia M3 los vehículos no son suficientes para el atendimiento de la demanda, incluso con un alto presupuesto. En esas instancias el nivel de servicio es bajo y no existen muchos cambios en las decisiones de contratación, apertura de centros de auxilio y almacenamiento de inventarios a medida que aumenta el presupuesto.
5. Conclusiones y perspectivas futuras
En este artículo, fue desarrollado un modelo biobjetivo de programación estocástica entera-mixta para el problema integrado de localización de centros de auxilio, distribución de productos y dimensionamiento de flota en operaciones de respuesta a desastres en contextos multi-periodo, multi-producto y con flota heterogénea. Además, son consideradas las incertezas inherentes a las situaciones. El modelo biobjetivo fue comparado con una versión mono-objetivo del mismo. Los resultados muestran que, en general, el modelo mono-objetivo ofrece buenas soluciones desde el punto de vista del atendimiento a la demanda e incluso minimiza los costos logísticos de ese atendimiento, lo que explica porque modelos mono-objetivo son ampliamente utilizados en la literatura para modelar operaciones en la gestión de desastres, incluso cuando son considerados objetivos contradictorios. Sin embargo, cuando los costos logísticos poseen una gran representatividad en la función objetivo, son encontradas mejores soluciones, desde el punto de vista de atendimiento la las víctimas, con el modelo biobjetivo. Fue observado que el modelo biobjetivo es de gran utilidad cuando el presupuesto disponible para realizar las operaciones humanitarias es limitado, permitiendo realizar el análisis del comportamiento de la distribución de los productos y atendimiento de la demanda ante diferentes niveles de presupuesto. Investigaciones futuras están orientadas al desarrollo de modelos matemáticos que consideren otras características importantes en situaciones de desastres como tiempo de transporte, reutilización de vehículos y costos sociales en la función objetivo.