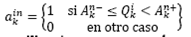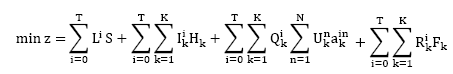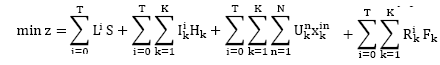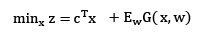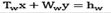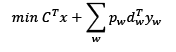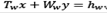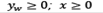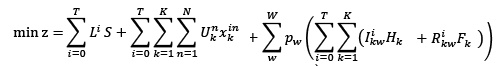1. Introducción
Desde el punto de vista económico y organizacional, la gestión de inventarios en lo que respecta a la planificación de pedidos, almacenamiento y distribución de medicamento, es fundamental en los procesos de prestación de servicios del sector salud. Esta importancia deriva, no solo de los altos precios de las medicinas y sus requisitos de almacenamiento y de control (Uthayakumar & Priyan, 2013), sino también de los altos niveles de servicio que se espera sean ofrecidos por el sector en materia de atención oportuna, para lo cual la disponibilidad de las medicinas es uno de los factores determinantes (Castrellón-Torres, Juan Pablo; Torres-Acosta, Jairo Humberto; Adarme-Jaimes, 2014). Sin embargo, la planificación de los procesos de fabricación, almacenamiento y distribución para satisfacer los requerimientos del mercado en términos de servicio y costos no es efectiva, a pesar de los avances que se han tenido en términos de tecnologías y modelos de planificación diseñados para apoyar estos procesos (Masoumi, Yu, & Nagurney, 2012). Parte de esta inefectividad radica en la complejidad de los problemas de distribución (Arango & Serna, 2015) y a la cantidad de actores involucrados y la diversidad de papeles que desempeñan en los procesos asociados a la planificación de la cadena de suministro. En muchas ocasiones estos procesos son soportados por tecnologías implementadas inapropiadamente para gestionar procesos colaborativos (Arango Serna, Adarme Jaimes, & Zapata Cortés, 2013). Por otra parte, también es necesario considerar la dificultad de tomar decisiones en escenarios inciertos, en donde la información sobre la demanda, la capacidad, tiempos etc., puede no estar disponible, o si lo está suele ser imprecisa. Bajo este marco, Shah (Shah, 2004) argumenta que las cadenas de suministro de medicamentos farmacéuticas están en la necesidad urgente de técnicas de optimización eficientes a fin de reducir los costos y aumentar la productividad y la capacidad de respuesta y que respondan las siguientes preguntas: ¿Cuáles son las incertidumbres importantes?, ¿Cómo se pueden controlar?, y ¿si es posible ofrecer soluciones valiosas desde diferentes puntos de vista? (King & Wallace, 2010).
En este artículo se responden las preguntas anteriores, para lo cual se desarrolla un modelo de programación estocástica de dos etapas para el tratamiento de la incertidumbre en la planificación de pedidos de medicamentos oncológicos. El modelo considera tres actores en la cadena de suministros: un comprador (farmacia), un productor (laboratorio) y un centro de distribución.
2. Revisión literaria
Muchos problemas de decisión contienen incertidumbre, la cual se origina por los acontecimientos en el pasado que no se conocen con exactitud debido a errores en la medición o dificultades en la toma de información, o sobre eventos en el futuro que no pueden ser conocidos con certeza (Tarim, Manandhar, & Walsh, 2006). La incertidumbre hace parte de los principales problemas de planificación de operaciones y la búsqueda de herramientas que faciliten su inclusión en el proceso de toma de decisiones está aún vigente.
Las incertidumbres en el proceso de suministro de la demanda tienen un impacto importante en la función de la producción, ésta se propaga a través de la cadena de valor y conduce a la adición de actividades de procesamiento ineficiente. La incertidumbre se expresa en preguntas como: ¿qué van a pedir los clientes? ¿Cuántos productos se debería tener en stock? y ¿será que el proveedor entregará los bienes solicitados a tiempo y de acuerdo a las especificaciones exigidas?.
Cualquiera de los modelos de planificación que trate de resolver las preguntas anteriores, debe proporcionar las decisiones a tomar en cada uno de los posibles estados. Sin embargo, la mayoría de procedimientos de planificación y programación asumen datos deterministas o trabajan con valores promedio (Chen, Li, & Tirupati, 2002), es evidente que el error en el que se incurre al no considerar la demanda como una variable aleatoria puede representar unos costos importantes debidos a la falta o al exceso de capacidad que se presenta al no coincidir la realidad con la previsión o incluso que la solución obtenida resulte finalmente ser no factible.
En la búsqueda de modelos más apropiados de planificación de operaciones logísticas en escenarios de incertidumbre, se han sugerido herramientas como la lógica difusa, la programación estocástica, programación dinámica, entre otras, las cuales han sido muy útiles. Trabajos como los realizados por Arango, Pérez & Serna [11] y Adarme, Arango & Cogollo [12], por ejemplo, han usado la lógica difusa para el tratamiento de la incertidumbre en los procesos de planificación de la cadena de suministro. Choi, Realff, & Lee (Choi, Realff, & Lee, 2005) por su parte proponen un novedoso marco algorítmico de optimización basado en programación dinámica, para resolver problemas de gestión de la cadena de suministro de varios productos y que involucra decisiones de fabricación y distribución con la demanda incierta.
En relación a la programación estocástica y, en particular, la optimización mediante escenarios, Parpas (Parpas & Rustem, 2006) la resalta como un instrumento adecuado para tratar la incertidumbre. Desde sus inicios, la programación estocástica ha encontrado aplicaciones diversas como paradigma eficaz para modelar decisiones bajo incertidumbre, y la gestión de inventario no ha sido la excepción. Algunos ejemplos en materia de investigación, son los trabajos realizados por Hammami, Temponi y Frein (Hammami, Temponi, & Frein, 2014), quienes usan la programación estocástica para la selección de proveedores teniendo en cuenta la incertidumbre en la tasa de cambio de la moneda y descuento de precio por cantidad de producto. Huang y Küçükyavuz (Huang & Küçükyavuz, 2008), presentan un modelo de programación estocástica de varias etapas para problemas de tamaño de lote en donde los costos, la demanda y los tiempos de entrega de pedidos tienen un tratamiento estocástico, el modelo se formula a través de un algoritmo de programación dinámica y un árbol de escenarios. Karuppiah, Martín y Grossmann (Karuppiah, Martín, & Grossmann, 2010) han desarrollados modelos de programación estocástica que buscan facilitar la toma de decisiones en los procesos de gestión de inventarios en ambientes de incertidumbre. Otros estudios pueden encontrarse en Marufuzzaman, Eksioglu y Huang(Marufuzzaman, Eksioglu, & (Eric) Huang, 2014), Sodhi y Tang (Sodhi & Tang, 2009), Santoso, Goetschalckx y Shapiro (Santoso, Ahmed, Goetschalckx, & Shapiro, 2005), Osmani & Zhang (Osmani & Zhang, 2013) entre otros.
En cuanto al análisis de la incertidumbre en empresas del sector farmacéutico, Guerrero, Yeung y Guéret (Guerrero, Yeung, & Guéret, 2013) presentan una metodología para encontrar políticas de control de inventario conjuntas en un sistema de distribución de un almacén y n minoristas de soluciones de infusión en un centro médico universitario en Francia. En el estudio son considerados estocásticos la demanda, la cantidad y políticas como también aspectos particulares del sector salud. El sistema es modelado usando cadenas de Marckov con el objetivo de minimizar los niveles de inventario en todo el sistema de distribución. Sousa, Liu, Papageorgiou y Shah (Sousa, Liu, Papageorgiou, & Shah, 2011) abordan un problema de asignación y planificación dinámica que optimiza la planificación global de la cadena de suministro de una compañía farmacéutica, desde las etapas de producción y la distribución a los mercados. El modelo explora diferentes costos de producción y distribución y las tasas de impuestos en diferentes lugares con el fin de maximizar el valor del beneficio neto de la empresa. Izady y Kimiagari (Izadi & Kimiagari, 2014) usan un modelo estocástico para determinar el número óptimo de centros de distribución y sus ubicaciones en una empresa del sector farmacéutico. El modelo se resuelve a partir de técnicas de simulación Montecarlo para generar un conjunto de posibles escenarios de la demanda y algoritmos genéticos.
3. Descripción del proceso de abastecimiento de medicamentos oncológicos
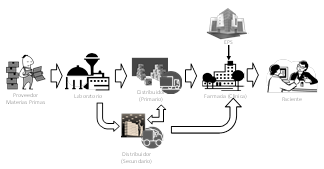
En la Fig. 1 se muestran las principales etapas en la elaboración y distribución de medicamentos. Cuando el proceso de fabricación y empaque finaliza en el laboratorio, los medicamentos son llevados a centros de distribución controlados por mayoristas. En algunos casos los fabricantes también pueden coordinar los procesos de distribución a través de proveedores logísticos de tercera parte (3PL). Los distribuidores mayoristas, incluidos los distribuidores primarios y secundarios, son responsables de mantener la integridad de los medicamentos desde su fabricación hasta el distribuidor minorista, que distribuye el medicamento a los pacientes. Los distribuidores son el vínculo crítico entre los fabricantes (laboratorio) y la red de farmacias, hospitales, clínicas y consultorios en todo el país.
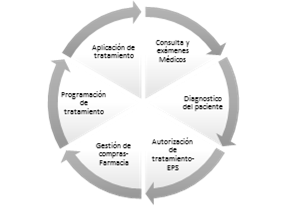
En Colombia, bajo el Sistema de Seguridad Social, el proceso de abastecimiento de medicamentos oncológicos, inicia generalmente con una consulta o cita médica en donde se realiza un diagnostico al paciente y se determina la medicación que deberá tomar para dar inicio al tratamiento, el cual debe ser autorizado por la Entidad Promotora de Salud (EPS), quien tarda aproximadamente 15 días en el proceso. Una vez autorizado el tratamiento, se da inicio al proceso de compra que puede tardar de 1 a 3 días. Posteriormente se planifica y aplica el tratamiento correspondiente en el paciente quien es sometido a nuevos exámenes, reiniciándose el proceso (ver Fig. 2).
Debido a la complejidad y urgencia de los tratamientos oncológicos, se recomienda que los hospitales mantengan inventarios de seguridad que soporten cambios no esperados en el proceso y que se presentan debido a emergencias o prioridades que deben tenerse con algunos pacientes. En este aspecto, y teniendo en cuenta los altos costos de los medicamentos oncológicos, la gestión de compras e inventarios puede ser una labor compleja en la que se debe asegurar no solo la eficacia del proceso, sino también su eficiencia. Por otra parte, en muchas ocasiones las políticas de inventario son establecidas en relación a comportamientos históricos y según niveles de rotación; sin embargo, como se ha visto, las decisiones tomadas sin tener en cuenta la incertidumbre presente en variables como la demanda o el tiempo de suministro, le agregan ineficiencia al proceso de compra de medicamentos.
De acuerdo a lo anterior, en el próximo capítulo se presenta un modelo que busca mejorar la gestión de inventarios de medicamento oncológicos, a partir de la inclusión de la incertidumbre en el proceso de toma de decisiones.
4. Formulación matemática del modelo de inventarios
Cuando el tiempo y la incertidumbre juegan un papel importante en el proceso de toma de decisiones, es necesario construir un modelo que permita adoptar políticas de decisión que correspondan con los eventos que se van manifestando en cada uno de los periodos que constituyen el horizonte de planeación (Escudero & Kamesam, 1995).
Partiendo de algunos conceptos aportados por Schumann (Schumann, 1999), se decidió desarrollar en este trabajo un algoritmo estocástico de dos etapas. Para tal caso, es necesario diseñar un modelo que combine la planificación estratégica y las decisiones logísticas tácticas con elementos sujetos a incertidumbre, como lo son: las cantidades a ser ordenadas, el precio, los tiempos de abastecimiento, entre otros. La incertidumbre presente en estas variables puede ser generada por muchos a aspectos, como por ejemplo el cambio de divisas en las importaciones, problemas de transporte, cambio o evolución de las patologías del cáncer en el paciente o cambios inesperados en su tratamiento, entre otros.
Para tratar eficazmente este tipo de incertidumbre se pueden analizar diferentes escenarios que pueden tener lugar durante el horizonte de planificación del proceso de compra de los medicamento. Como estrategia de solución propuesta, los modelos de programación estocástica de dos etapas, permiten hacer un análisis por escenario considerando dos etapas para esto: la primera consiste en hacer pedidos a un primer proveedor (distribuidor primario) relacionado directamente con el laboratorio fabricante y aprovechar los descuentos por cantidad, lo que llevaría a tener un exceso de inventario dado el caso. Con este primer proveedor los tiempos de entrega no son inmediatos, por lo que si las existencias del medicamento son insuficientes para abastecer la demanda se podría tener una rotura de inventarios. La segunda etapa en el modelo corrige esta posible eventualidad, y se acude a un segundo proveedor (distribuidor secundario) para cubrir la demanda faltante. Este proveedor tiene un tiempo de respuesta más oportuno pero el medicamento es más costoso.
El procedimiento anterior se formula inicialmente como un modelo determinístico, el cual para dar cabida a las dos etapas de decisión se rediseña en un modelo de programación estocástica, como se presenta a continuación:
4.1. Modelo determinístico para la gestión de inventarios
El modelo que se presenta a continuación, busca minimizar el costo total representado por los costos de pedido, costo de almacenamiento, costos del producto y los costos incurridos por subestimar la demanda. El modelo admite descuentos por cantidad. A continuación se definen cada una de las variables usadas en el modelo y se hace una representación de la función objetivo.
i= 1, 2, 3,…., T: periodos de tiempo
k= 1, 2, 3,…, K: productos
n= 1, 2, 3,…, N: intervalos de descuentos
Q ik = cantidad de pedido del artículo k en el periodo i
I ik = cantidad de inventario del producto k en el periodo i
R ik = unidades del producto k pedidas al centro de distribución secundario en el periodo i
S= Costo de pedido
𝐻𝑘 = Costo de almacenamiento del producto k por unidad periodo
U nk = Costo del producto k en el intervalo de descuento n.
F k = Costo del producto k ofrecido por el centro de distribución secundario.
A nk , A nk += límite inferior y superior del intervalo de descuento n
= número muy grande
L i =1 si se hace un pedido en el periodo i, o igual a 0 sino se hace ningún pedido
La función objetivo no es una función lineal por el término 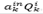 , por lo tanto este producto será representado por la variable
, por lo tanto este producto será representado por la variable 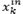 con el cual la función objetivo propuesta llega a ser:
con el cual la función objetivo propuesta llega a ser:
Para la formulación de las restricciones, se debe tener en cuenta que las variables 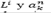 están asociadas a la cantidad de pedio (Q
ik)
; por lo tanto las primeras restricciones se formulan con el fin de guardar la correspondencia entre estas variables (ver Tabla 1).
están asociadas a la cantidad de pedio (Q
ik)
; por lo tanto las primeras restricciones se formulan con el fin de guardar la correspondencia entre estas variables (ver Tabla 1).
4.2. Modelo estocástico de dos etapas
Si en el modelo anterior la demanda di k es aleatoria es necesario considerar dos características adicionales: En primer lugar, se debe modelar la disponibilidad de la información en el tiempo, e indicar qué tipo de decisiones se puede hacer en cada una de las distintas etapas. En segundo lugar, con el fin de optimizar una solución propuesta, ésta debe ser comparada (ajustada) con otro criterio propuesto, el cual en un marco de aleatoriedad puede ser algo difícil. En la programación estocástica, se pone mucho énfasis en la decisión que se toma, dados los recursos actuales, las incertidumbres del futuro y las posibles acciones de ajustes. En la modelación estocástica la incertidumbre en los datos del problema se captura a través de un conjunto de escenarios (w) dando origen al "análisis de escenarios" en el cual se establece un árbol de escenarios y una función objetivo la cual se elige para representar el riesgo asociado a la secuencia de decisiones que se toman.
En el problema analizado, los escenarios están asociados a los valores que toma la demanda en cada periodo, de tal manera que:
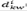 = demanda del producto k en el periodo i sobre el escenario w
= demanda del producto k en el periodo i sobre el escenario w
pw = probabilidad asociada con el escenario w.
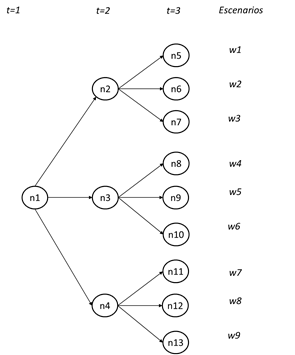
En la Fig. 3 se muestra un árbol de escenarios en donde los nodos representan los posibles valores de la demanda en tres periodos de tiempo, por su parte los escenarios resultan de la combinación de estos nodos en el horizonte temporal contemplado; así por ejemplo el escenario w4 está compuesto por los nodos n1 , n3 , n8 .
Entre las diferentes metodologías usadas para solucionar problemas de programación estocástica, sobresale la programación estocástica de dos etapas propuesta inicialmente por Dantzing (1955) y que busca minimizar los costos asociados a la primera etapa y minimizar el costo esperado con la segunda etapa. Un modelo de programación estocástica de dos etapas puede ser representado de la siguiente manera:
Sujeto a:
Ax=b
x ≥ 0
En donde EW G(x,w) es el valor esperado de la función G(x,w) la cual es igual a:
Sujeto a:
y ≥ 0
El primer componente en la función objetivo representa la primera etapa de decisión en la que hay que tomar un conjunto de decisiones (representadas por las variables aleatorias x) sin contar con información completa sobre algunos eventos aleatorios. Posteriormente uno de los posibles escenarios w se cumple y la información es completada, dando lugar a la segunda etapa del modelo estocástico en la que se toman decisiones correctivas [las cuales se representan por la variable aleatoria y). Si solo se consideran probabilidades discretas y se unen las dos etapas en un solo modelo lineal, el resultado sería el siguiente modelo lineal determinista equivalente:
Sujeto a:
Ax = b
El modelo de inventario propuesto puede ser reformulado como un problema de programación estocástica de dos etapas, en donde la primera etapa consiste en determinar la cantidad de pedido al primer proveedor (Q ik ) y en la segunda etapa se establecen los niveles de inventarios del producto k (I ik ) y la cantidad de pedido solicitada al segundo proveedor (R ik ); con eso el modelo de la ecuación (2) queda convertido en el siguiente modelo de programación estocástica:
En la siguiente Tabla 2 se presentan las restricciones asociadas:
5. Aplicación del modelo y análisis de resultados
En esta sección se presenta la instancia usada para evaluar el modelo formulado. Para este fin se usó el software de optimización GAMS (Sistema General de Modelaje Algebraico) versión 24.2.1 el cual es un software robusto que permite solucionar problemas de este tipo con relativa facilidad. Seguidamente se hará la presentación de los resultados tanto del modelo determinístico como del estocástico.
5.1. Aplicación del modelo estocástico de dos etapas
Para la selección de los medicamentos usados en el modelo, se tuvieron en cuenta medicamentos con un costo representativamente alto y alta rotación, como son la Sandostatina, Exjade y Tasigna (Marcas registradas de Medicamentos oncologicos de la Corporación Farmaceutica Novartis) del que se utiliza, para los tratamientos relacionados con la leucemia, tumores endocrinos e insuficiencia renal.
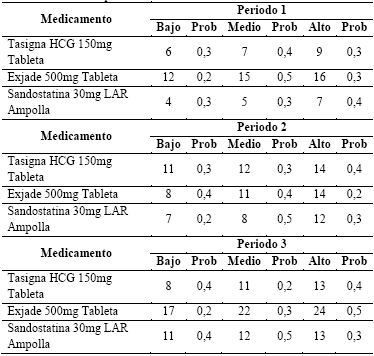
Para el análisis estocástico, se ha definido que la demanda en cada periodo puede tener un comportamiento alto, medio o bajo; en la tabla 3 se muestra cada posible valor de la demanda con su respectiva probabilidad de ocurrencia.
A partir de esta información es posible generar un árbol de escenarios que combina, para cada medicamento, los posibles valores de la demanda en cada periodo del horizonte de planificación. Los escenarios se generan de la siguiente forma: por cada medicamento, el primer nodo constituye el punto de partida de tres posibles valores de la demanda, los cuales a su vez se constituyen en puntos de partida para la demanda en un segundo periodo y así sucesivamente. En total se generan de 3^3= 27 posibles escenarios (tres posibles valores de la demanda por tres periodos) por medicamento, para un total de 81 escenarios.
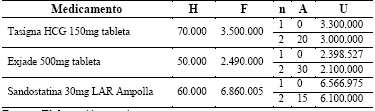
En la Tabla 4 se muestran los demás valores necesarios para ejecutar el modelo como los costos de almacenamiento (H), costos de cada medicamento segundo proveedor (F), intervalos de descuento (n), valor del intervalo (A), costo del medicamento con descuento (U) y un costo de pedido de 400.000 pesos como valor arbitrario.
5.2. Resultados del modelo determinístico
En la Tabla 5 se muestra los resultados obtenidos para el modelo determinístico (los valores de la demanda tomados corresponden a la demanda media). Como se puede apreciar solo se hace un pedido para los tres productos durante los tres periodos que se planifica. Si bien el costo de almacenamiento se incrementa, el descuento que se obtiene por cantidad de pedido compensa este incremento en el costo.
En este modelo los pedidos realizados al segundo proveedor no se consideran, debido a que al ser un modelo determinístico la demanda y frecuencia de pedidos son conocidos, por lo que las roturas pueden ser evitadas.
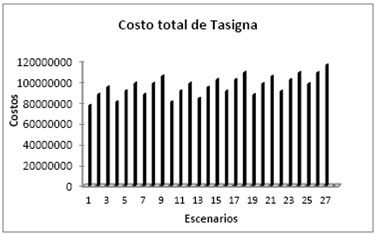
5.3. Resultados del modelo estocástico
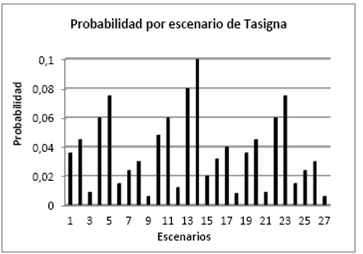
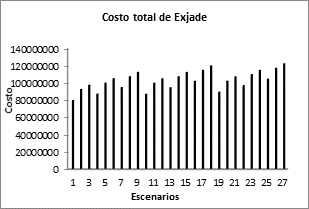
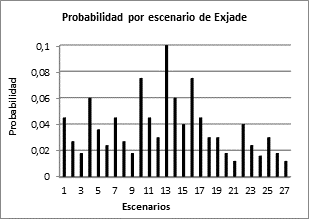
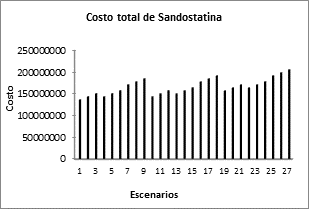
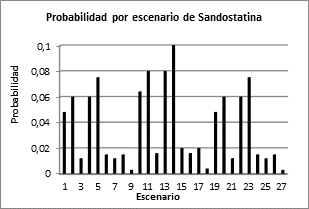
En las Figs. 4, 6, 8 se muestran los costos del modelo de gestión de inventarios para cada medicamento y los escenarios respectivos para cada uno. Las probabilidades de ocurrencia para cada escenario se muestran por cada producto en las Figs. 5, 7, 9 respectivamente. Como se puede apreciar en estas figuras, el escenario 13 es el que mayor probabilidad de ocurrencia tiene y su costo también es uno de los más bajos. Sin embargo el escenario 13 solo es un escenario de los 27 posibles. Para encontrar una solución general en el modelo estocástico de dos etapas, debe calcularse el costo esperado a partir de la suma de los costos asociados a cada medicamento en relación a los posibles escenarios, ponderados por sus probabilidades de ocurrencia. Este procedimiento es explicado más adelante.
Para interpretar los resultados en el modelo estocástico, es necesario entender el concepto de las dos etapas: Como se explicó en secciones anteriores, en la primera etapa se toma una decisión que busca minimizar los costos en los que se incurre cuando es necesario ajustar dicha decisión al escenario que tiene lugar. Este ajuste define otro proceso de decisión y por lo tanto una segunda etapa.
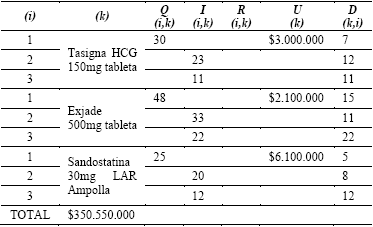
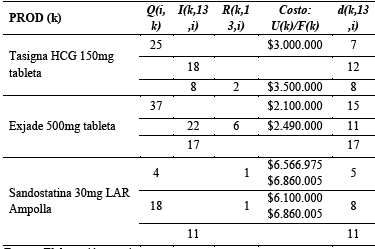
En la Tabla 6, se muestra el resultado del modelo considerado, en la primera etapa se hace un primer pedido para la Tasigna, Exjade y Sandostatina de 25, 37 y 4 respectivamente y un segundo pedido de 18 unidades para la Sandostatina. Sin embargo esta decisión no se ajusta a un escenario en particular, por el contrario debe ser ajustada a cualquiera de los 27 escenarios que pueden tener lugar para cada medicamento. La importancia de la solución encontrada por este método, consiste en que se minimiza el costo esperado por hacer dichos ajustes. En la siguiente tabla se muestra uno de esto escenarios (escenario 13) el cual tienen una probabilidad de ocurrencia del 10%. En este escenario se presenta un valor diferente de la demanda a la cantidad pedida en la primera etapa, por lo tanto debe acudirse a un segundo proveedor, quien oportunamente y a un mayor precio facilitará las unidades faltantes del medicamento k en el periodo i (ver columna R(k,13,i)).
Para este escenario en particular se obtiene un costo total de $328’857.910 (más costos de pedido), valor que está sujeto a una probabilidad de ocurrencia del 10%. El costo esperado, asumiendo todos los escenarios en el modelo estocástico, es de $350.336.915 el cual es ligeramente menor al resultado obtenido en el modelo determinístico; sin embargo esto es solo un costo esperado y depende de las probabilidades que acompañan a cada escenario. En algunas ocasiones la demanda tendrá un valor menor a la demanda media considerada en el modelo determinístico, y en otras ocasiones será mayor.
6. Conclusiones
En este artículo se desarrolló un modelo estocástico de dos etapas para medicamentos usados en tratamientos oncológicos: Exjade, Sandostatina y Tasigna. El modelo ofrece una alternativa para el manejo de la información en condiciones de incertidumbre, el cual en comparación con los modelos determinísticos, pueden generar soluciones más económicas y ajustadas a escenarios más concretos. En el caso ilustrado por ejemplo, algunos escenarios tienen un costo mucho menor a la solución determinística la cual está basada, algunas ocasiones, en valores promedio de la demanda, los cuales no pertenecen necesariamente a un escenario en particular, por lo que los costos asociados a posibles ajustes se incrementarían.
El uso de modelos determinísticos para la gestión de inventario de medicamentos bajo condiciones ideales de demanda y frecuencia de pedidos, no es garantía de resultados efectivos. La incertidumbre asociada a los pacientes y sus tratamientos, al igual que el comportamiento de los proveedores, no debe ser ignorada en el proceso de toma de decisiones. Como se pudo apreciar en este estudio, el uso de la demanda como una variable determinística puede llevar a sobre costos ocasionados por ajustes necesarios en el proceso de planificación. El modelo estocástico minimiza el impacto de estos ajustes al considerar que las decisiones deben ser tomadas teniendo presente los posibles escenarios.
El modelo estocástico de dos etapas propuesto, además de ser fácil de interpretar, es de fácil implementación y demuestra que la inclusión de la incertidumbre en el proceso de toma de decisiones en lugar de volverlo más complejo, lo enriquece y potencializa al obtener resultados que se ajustan con mayor facilidad a las condiciones reales.