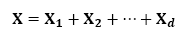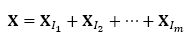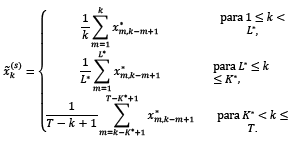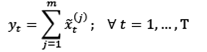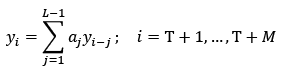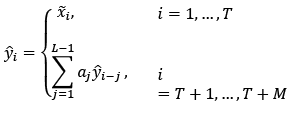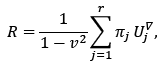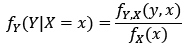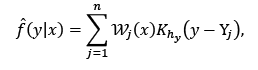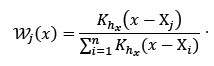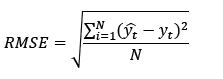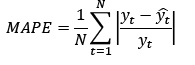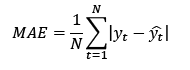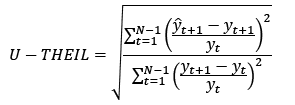1. Introduction
Wind energy is the fastest growing source of power generation in Brazil as a result of the implementation of The Brazilian government’s Decennial Energy Plan - PDE 2024 [1], which indicates that the participation of wind energy in electricity generation matrix is expected to reach nearly 12% by 2024 with the expansion of at least 24 GW of installed wind farms. For this, the Brazilian wind industry should try to keep a steady 2 GW annual growth, as well as to guarantee a competitive wind energy price at the auctions. This way the industry, as a whole, should attract new investments.
Forecasts of wind energy depend mainly on the wind speed, and given its stochastic nature, in order to include the wind speed into the optimal dispatch, reliable and accurate predictions are required. Therefore, the integration of the wind power into the Brazilian system is a rather difficult task. For operational purposes this kind of forecasts are based on short-term horizons, for example, up to 24 hours ahead.
Different methods for hourly time series forecasting [2] could be employed, i.e., statistical methods (ARIMA, Kalman filter, probabilistic forecasting, etc.), computational intelligence methods (artificial neural networks, support vector machines, fuzzy logic and neuro-fuzzy systems) and hybrid methods that combine approaches based on statistical techniques and computational intelligence and other techniques.
Nonetheless, almost all of these approaches provide a single expected value for each forecast horizon, i.e., a point forecast. The technical literature reports that point forecasts, which are also deterministic forecasts, are the major approaches employed [2]. Despite of that, point forecast has a relevant shortcoming, any information about the deviation from the predicted values is not provided, and therefore, the distribution of the forecasting errors is ignored, what limit its use in decision-making processes.
Using point forecast could lead to not accurate predictions of wind power generation, making the power system unreliable. Underestimated forecasts of wind power might cause wind power curtailment or that conventional plants operate in part-load due to the system operator commit fewer wind power units than necessaries, and consequently, increase generation costs. Otherwise, if the forecast of the wind power is overestimated, the system will have a power supply shortage unless sufficient spinning reserve has been committed to the power system.
The existing approaches for wind speed and wind power do not respond satisfactorily the accuracy required to be part of the optimal Brazilian hydro-thermal wind dispatch. Therefore, as an alternative to overcome this difficulty one could use probabilistic forecasting through the probability density function, instead of the point forecasts provided by the existing approaches to model the wind speed / wind energy.
Indeed, the majority of the available methods are carried out in two stages: in the first a model (be it statistical, computational intelligence or even hybrid) is fitted to predict the wind speed in order to produce hourly wind speed point forecasts. On the second stage, these forecasts are taken to the wind turbine power curve that outputs the corresponding wind energy [3,4]. See also [5] for a state-of-the-art report on the subject.
The main criticism to these approaches lies on the fact that there are other meteorological variables, besides the wind speed, that are not taken into account when using solely the power curve on the second stage to produce the wind energy forecast. Such one-to-one relationship is just a guideline. For the same wind speed there are different wind energy possibilities as can be checked on wind farm in operation.
Also, instead of using conventional time series methods to model the wind speed, such forecast will be produced by SSA (Singular Spectrum Analysis) to extract the noise-free signal of the wind speed series [6,7] to produce more accurate wind speed forecasts.
This article proposes a hybrid methodology for modeling the wind power generation, through three stages, to obtain the full probability density function of the wind energy. For this, in the first stage using SSA (Singular Spectrum Analysis) it is obtained the wind speed forecasts. In the second stage is calculated the estimation of the density function of the wind power employing Conditional Kernel Density Estimation; and in the third stage, for a given particular wind speed forecast is calculated the density forecast function of the wind power. The remainder of this paper is organized as follows: in section 2 presents a brief literature review, and gives a description of SSA and kernel density estimation. Then, in section 3 the methodology to modelling wind speed and wind power is defined. Next, in section 4 it is shown the results based on kernel density estimators and wind speed forecast. The paper ends with some conclusions and remarks in section 5.
2. Literature review
The wind speed forecasts for wind power generation and operation planning in power systems focuses mainly on short-term forecast, due to the power system operations, such as electricity market clearing, regulation actions, power system planning for unit commitment and dispatch are held within specified periods ranging from 1 to 24 hours ahead.
Nonetheless, due to the fact that wind power generation depends on wind speed, several methods have been developed. Usually, these methods are classified into three categories: physical, statistical and hybrid approaches. The first are physical methods, which establishes a lot of considerations to predict the wind speed according to the physical description of the atmosphere. In this case, information provided by the weather service in most of the procedures transform the coarse grid of the wind speed and other climate variables to the characteristics of the terrain where is located the wind farm. The second are the statistical methods, which use approaches like ARIMA models, Artificial Neural Network (ANN) models or combination of both, to obtain the relationship of the measured power or wind speed data. The third are hybrid models, which can be considered as a combination of different approaches of physical and statistical models or combination of these models or combination of models for the short-term and for the medium-term, in order to improve overall performance forecasts.
Traditionally, the most widely used model for prediction has been ARIMA, although there had been previous attempts to predict the wind speed. The first work considering wind power forecasts was proposed by [8], in which it is fitted an autoregressive process (AR) to wind speed data transformed to make their distribution approximately Gaussian and standardized to remove diurnal nonstationarity. Despite the wind speed time series and wind energy present a highly nonlinear dynamic, different works have opted for linear approaches, such as in [9-12].
Similarly, for wind speed prediction it was used the Kalman filter to estimate the parameters of AR and ARMA models, as indicated in [13,14]. In [15] it is also used a state-space model to be optimized with a Kalman filter to predict the wind speed over the North Atlantic Ocean. Other approaches like ARFIMA in [16] and ARFIMA-FIGARCH in [17] are employed for the same purpose. In the case of non-linear statistical models, STAR and SETAR are applied in [18].
Different Artificial Neural Network models architecture such as feed-forward neural networks (FNNs), multi-layer perceptrons (MLP), recurrent neural networks (RNNs), radial basis function (RBf) NNs, Adaline networks, have been used not only for wind speed forecast, but also for wind power generation [18-20], where its performance is improved. In [21] is used Adaptive Neuro-Fuzzy Interface System (ANFIS), to forecast wind speed and wind power through a training set that includes wind speed and direction data.
In the case of physical models, most of the physical approaches used to forecast wind speed is known as a Numerical Weather Prediction (NWP), which solves complex mathematical models, i.e., conservation equations numerically using current weather conditions like temperature, direction, pressure, surface roughness and obstacles at the given site. These methods increase the real resolution of NWP model in order to achieve accurate prediction of the weather [22]; however, they are not effective for short-term forecasting due to their computational costs, see [23].
All of these described approaches offer a point forecast, while methods like quantile regression, copulas or conditional density kernel estimation give a probabilistic forecast; specifically, different kernel estimators have been used to compute the conditional density of the wind power output. In [27] it was employed the CKDE, while in [28] it was applied the two-step CKDE [30] and the Parzen-Rossenblatt estimator [30,31], in which the two-step CKDE led them to results slightly more accurate than those produced by Parzen-Rosenblantt estimator. In [32] the authors used the time adaptive CKDE with time adaptive. Following the same approach of those works this paper will be focused on Conditional Kernel Density estimator.
2.1. Singular Spectrum Analysis (SSA)
SSA is a non-parametric technique for analyzing and forecasting time series, which relies exclusively on data [24]. Furthermore, the SSA does not require the stationary assumption of time series, and allows the decomposition of a time series into various additive components [7].
Basically, the implementation of SSA involves three stages: decomposition, reconstruction and forecasting. These three stages are described in the following subsections.
2.1.1. Decomposition
The decomposition stage has two steps: embedding and singular value decomposition (SVD).
2.1.1.1. Embedding
Embedding consists of a moving window of length L that runs through the time series 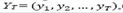 obtaining in each step a column of the trajectory matrix as eq. (1), whose total number of columns is equal to K = T - L + 1.
obtaining in each step a column of the trajectory matrix as eq. (1), whose total number of columns is equal to K = T - L + 1.
The number of components L extracted from the time series is determined by the window length. The parameter L is a sufficiently large integer value, but no greater than T/2, i.e., 2≤ L≤ T/2[6,7].
2.1.1.2. Singular value decomposition (SVD)
Using the SVD the trajectory matrix X in eq. (1) can be expressed by a sum of the elementary matrices and represents a sum of rank-one bi-orthogonal elementary matrices as follow:
where each component in eq. (2) is expressed by 
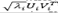 , d is the number of nonzero eigenvalues, of the matrix 𝐗𝐗T, denoted by 𝜆1,…,𝜆𝐿 in decreasing order of magnitude (
λ1 ≥ ... λL ≥ 0
). 𝑈𝑖 and 𝑉𝑖 denote the left and right eigenvectors of the trajectory matrix, and 𝑈1,…,𝑈𝐿 is an orthonormal system, i.e., (𝑈𝑖,𝑈𝑗) = 0 for 𝑖≠ 𝑗 and ‖𝑈𝑖‖=1, and corresponds to the eigenvectors of the matrix 𝐗𝐗T. The set {𝑈𝑖,
Vi
, 𝜆𝑖} corresponds to an eigentriple ( i = 1,...,d.
, d is the number of nonzero eigenvalues, of the matrix 𝐗𝐗T, denoted by 𝜆1,…,𝜆𝐿 in decreasing order of magnitude (
λ1 ≥ ... λL ≥ 0
). 𝑈𝑖 and 𝑉𝑖 denote the left and right eigenvectors of the trajectory matrix, and 𝑈1,…,𝑈𝐿 is an orthonormal system, i.e., (𝑈𝑖,𝑈𝑗) = 0 for 𝑖≠ 𝑗 and ‖𝑈𝑖‖=1, and corresponds to the eigenvectors of the matrix 𝐗𝐗T. The set {𝑈𝑖,
Vi
, 𝜆𝑖} corresponds to an eigentriple ( i = 1,...,d.
2.1.2. Reconstruction
The reconstruction stage is composed of two steps: grouping and diagonal averaging. In the grouping step the d elementary matrices obtained from the SVD step are grouped into mutually exclusive groups (clusters). Furthermore, the matrices are converted into time series through the so-called average diagonal procedure and, at the end it is obtained the additive components that make up the time series.
2.1.2.1. Grouping of the eigentriples
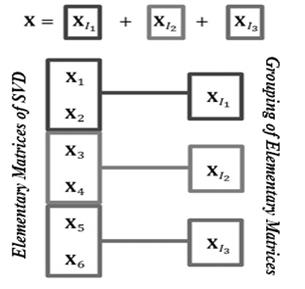
In this step, the elementary matrices Xi are split into several groups and summed within each group. For this, the indexes {1,...,d} are segmented into m (m <d) disjoint subsets { I1,...,Im }, such that the corresponding elementary matrices Xi indices, in the same group, are classified into the same cluster and added in this sequence. Thus, the trajectory matrix can be expressed by the sum of m matrices:
For example, if d = 6 and m = 3, the six elementary matrices are grouped into three clusters, as illustrated in Fig.
1. The procedure of choosing the sets I1,...,Im is called the eigentriple grouping.
2.1.2.2. Diagonal averaging
In this stage, each matrix obtained by clustering process is transformed into a time series of length T [25]. Consider a matrix Xi ( s =1,..,m with elements 𝒙
𝑖j
,1 ≤𝑖 ≤ 𝐿, 1≤ 𝑗 ≤ 𝐾 Let be  , and T = L + K - 1. Additionally, let be
, and T = L + K - 1. Additionally, let be 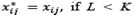 < K and
< K and 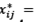
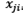 otherwise. Thus, the matrix
otherwise. Thus, the matrix 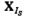 is transform into the series
is transform into the series 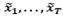 as follows:
as follows:
The diagonal average of the matrix 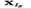 ( s=1,..., m builds the series
( s=1,..., m builds the series 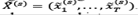 . Therefore, the initial series y1,..., yT is decomposed into a sum of m series:
. Therefore, the initial series y1,..., yT is decomposed into a sum of m series:
2.1.3. Forecasting
To obtain forecasts using SSA the basic requirement is that the time series satisfies the relations Linear Recurrent Formula (LRF), as indicated in [25]. The serie YT =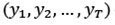 satisfies the LRF order L -
1 if:
satisfies the LRF order L -
1 if:
The main assumption is that the window length L is chosen in such way to separate the signal from noise. The predictions are performed using the r chosen eigentriples as follows:
where  are the values obtained from the reconstructed series in eq. (4), while
are the values obtained from the reconstructed series in eq. (4), while 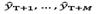 indicate the forecasts M steps ahead.
indicate the forecasts M steps ahead.
Also in eq. (7), the coefficients form the vector 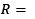
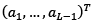 are determined as follows [26]:
are determined as follows [26]:
where the vector 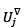 denotes the first L - 1 components of the eigenvector
denotes the first L - 1 components of the eigenvector 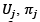 , is the last element of
, is the last element of  and
and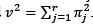 .
.
2.2. Conditional kernel density forecast methodology
The basic idea of the conditional kernel estimation is to provide a density (pdf) of a random variable Y given a random variable X = x. This technique is classified as non-parametric, and presents an advantage over other approaches because it estimates the underlying distribution from the data, without supposing a family distribution. The kernel density estimator computes a smooth density estimation from the data sample by placing to each sample point a function representing its contribution to the density. The distribution is obtained by summing all these contributions.
2.2.1. The Conditional Kernel Density Estimator (CKDE)
Conditional density estimation provides the assessment of the pdf of a random variable Y, given an explanatory variable X with the value of x known as follows:
The expressions in (9) is unknown, for this reason, this density function is estimated from the data, i.e., with the sample available and using the non-parametric estimator known as CKDE. According to [29], the conditional density estimation is given by
where
and where N is the length of the sample, Kh(·) = K(·/h)/h is a kernel function and h the bandwidth parameter. This estimator has two bandwidths, hx and hy , that controls the amount of smoothing; i.e., hy controls the smoothing of each conditional density and hx controls the smoothing of the explanatory variable.
It is possible to observe that the CKDE requires double kernel estimation, i.e., kernel density estimation in the y direction as indicated in eq. (10) and the other in the 𝑥 direction as in eq. (11). For a given 𝑥, the density function of the random variable 𝑌 is built up by applying kernel density estimation to the sample of values of 𝑌, weighting each 𝑌 value according with the contribution of 𝑋 given by the value 𝑥.
3. Methodology
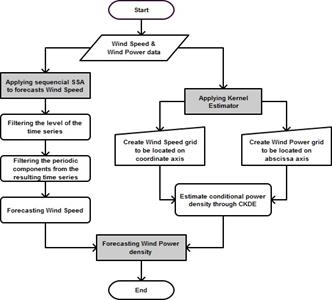
This session brings an overview of the non-parametric proposal to obtain probabilistic short-term forecasts of wind power. This methodology is based on the non-parametric techniques SSA and CKDE described previously. The overall methodological strategy of probabilistic forecasts of wind generation used in this paper is an adaptation of the two stages of point forecast approach of wind power generation, whose structure is shown in Fig. 2 and is detailed as follows:
First stage: use SSA sequentially to generate hourly forecasts of wind speed h steps ahead.
Second stage: based on historical data of wind speed and wind power estimate the stochastic power curve, i.e., the conditional density of 𝑃 𝑤𝑖𝑛𝑑 𝑝𝑜𝑤𝑒𝑟 𝑤𝑖𝑛𝑑 𝑠𝑝𝑒𝑒𝑑) through the CKDE, which is, basically, the conditional probability density of power at a certain wind speed value.
Third stage: use the wind speed predicted values at the first stage in combination with the stochastic power curve estimated at the second stage to generate the wind energy density forecasting.
4. Results
4.1. The wind power and wind speed data
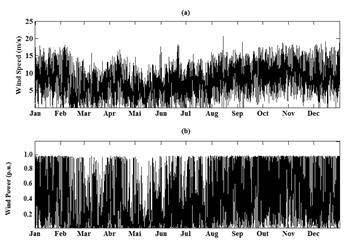
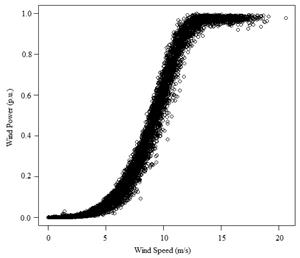
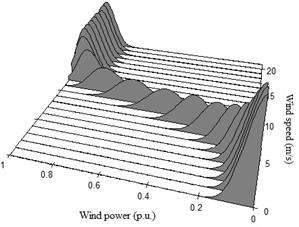
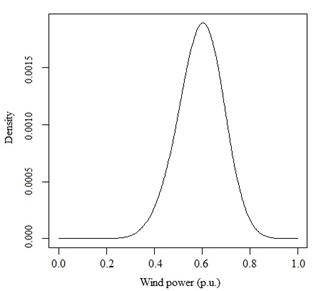
To illustrate the application of the described method it was considered a wind farm, but for confidentiality reasons it is not possible to publish its name and the location of the park. The dataset is composed of observations ranging from January 1, 2007 up to January 1, 2008, a total of 8784 hourly data of wind speed in m/s (Fig. 3) and wind power in p.u. for one turbine. In Fig. 4 it is shown the wind power output versus wind speed for the entire period, thereby generating the power curve covering the whole dataset. In this work it is used both: Rssa [33] and hdrcde [34] packages available in R software.
In what follows, the three stages approach proposed in this paper is applied to the Brazilian wind farm dataset.
4.2. First stage: wind speed forecast
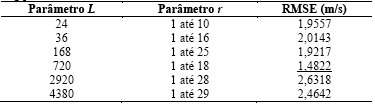
The first stage of the modelling process to forecast wind speed starts by choosing the L and r hyperparameters. To get better separability of the periodic components it is recommended that the window length L be proportional to the seasonal period (24 hours), as indicated in the first column in Table 1.
For each value of L it was applied SSA and the hyperparameter r was chosen by enumeration, i.e., it was incorporated one by one component until one finds a value that minimizes the root mean square error (RMSE) between the observed series and the forecasts given by eq. (12). Thus the hyperparameters L and r were set at 720 and 18 respectively, as indicated in Table 1. Notice that the r value in this process in only used with the purpose of determining L.
With the identification of L = 720, starts the second step of SSA decomposition stage, i.e., the grouping of eigentriples via cluster analysis, in particular, using agglomerative hierarchical method. This information is used in SSA procedure to extract the level (first chart of Fig. 5), that corresponds to the first component of the time series as can be seen in Fig. 6 identified as Level Component.
Having extracted the level, the second stage of SSA is applied to reconstruct the time series. The residuals are considered the new time series on which it is applied again SSA to extract the periodic components that maybe present, as can be identified in Fig. 7 for almost all the eigenvectors. Reconstructing the time series was obtained from 259 out of 720 eigentriples. The reconstructed time series is shown on Fig. 7 and the resulting wind speed forecasting for 24 hours ahead on Fig. 8.
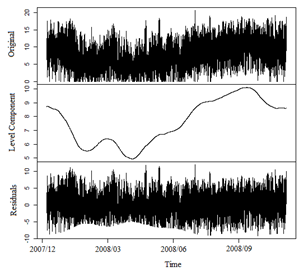
Source: The authors.
Figure 6 Original wind speed time series, Reconstructed series for level component and Residuals.
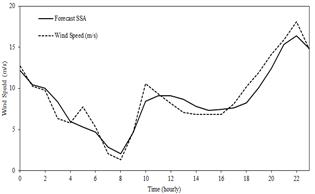
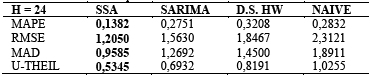
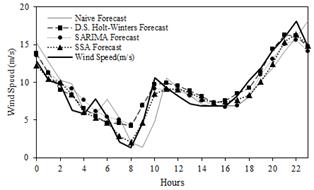
In order to compare the performance of the SSA forecast, other models like double seasonal Holt-Winters and SARIMA were fitted to the data. Naïve estimator is also used for this purpose and all these results are presented in Fig. 9. A numerical comparison is made via some error measures as mean absolute percentage error (MAPE), root mean square error (RMSE), mean absolute error (MAE) and U-THEIL depicted in Table 2 and given by eq. (13), (14) and (15), respectively. The results of these statistics, in bold, indicate that SSA have a better performance in comparison with the other models.
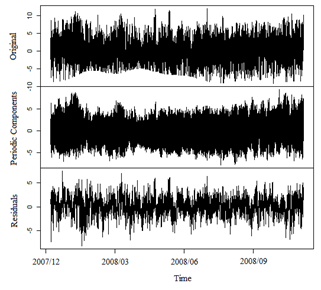
Source: The authors.
Figure 7 Original time series, Reconstructed series for periodic components and Residuals.
4.3. Second stage: stochastic power curve estimation
The second stage employs kernel estimators to obtain the stochastic power curve, where the full density function is estimated by repeating the conditional kernel density given by eq. (10) and eq. (11). Thus, it is necessary to create a grid with the wind power values (𝑝) ranging from zero up to the wind farm capacity, or like in this study up to the turbine capacity. Variations in 𝑝 are obtained by small increments until the established capacity.
Similarly, it is required to create a grid for axis 𝑥 with the wind speed values ranging from zero up to few meters above the maximum wind speed recorded in the database used. This work chooses the speed of 20 m/s as the maximum possible wind speed, because the maximum wind speed recorded in database is very close to this value. Notice that the discretization for both wind power and wind speed must be carried out at regular increments.
Using these grids and eq. (10) and (11), it is estimated the conditional density of wind power. This result is depicted in Fig. 10.
Source: The authors.
Figure 9 Wind speed (m/s) forecasting 24 hours ahead for different methodologies.
To produce an estimate of the conditional density of wind power production in each discrete value, the wind power should be conditional on a specific wind speed. These estimates are stored to be used in the next stage of the methodological framework.
4.4. Third stage: wind power density forecast
Considering the estimation of the conditional probability density of wind output, calculated in the previous stage, and the wind speed forecasts generated by applying sequential SSA in the first stage, it is obtained the corresponding conditional wind power density forecast. In particular, assuming wind speed forecasts values of 6 m / s and 11 m / s and using the estimated stochastic power curve, one can obtain the respective probability density forecast of wind power conditioned for these two wind speeds, which is shown in Fig. 11.
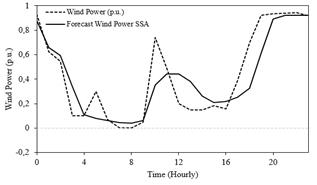
For each forecast of the wind speed CKDE provides a full probability density function for wind generation. Even though, the purpose of this work is density forecasting, it was evaluated point forecast accuracy using the mean of the distribution as the central location, i.e., a possible point forecast. Analogous to the wind speed forecast, it will be used RMSE, MAE and U-THEIL to evaluate wind power point forecast. Fig. 12 shows wind power forecast take into a count the wind speed forecasted by sequential SSA.
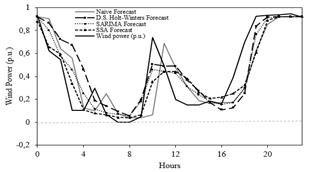
Using wind speed forecasts provide by the Naïve method, Double seasonal Holt-Winters and SARIMA model and CKDE it is possible to generate the point forecast for the wind energy production as can be seen in Fig. 13 for each model, while in Table 3 are displayed the results of the error measures for the different approaches.
According to [35,36], the mean of a density forecast is considered the optimal point forecast for a quadratic loss function. This suggests the use of the MAE and the RMSE as the goodness of fit criteria. The RMSE and MAD statistics are expressed as a percentage of the installed capacity. The results of the error measures in bold in Table 3, show that the sequential SSA for wind speed provide a better performance.
Source: The authors.
Figure 13 Wind power (p.u.) forecasting 24 hours ahead for different methodologies.
5. Conclusions
This paper proposes a new methodological framework for modeling short-term wind power generation and captures the uncertainty concerning to wind speed. The developed work provides insight on how to obtain forecasts of wind power probability density function by applying sequential SSA and CKDE. For short-term wind speed forecast it is used SSA approach that proved to be a robust alternative to produce wind speed forecast. The comparison with other methodologies to produce wind speed forecast, show that an improvement of the forecasts for the wind energy is improved considerably using the proposed method in this paper. As a future work, it is suggested to incorporate other explanatory variables such as direction, temperature and air pressure to modeling wind speed and evaluate other kernel density estimator that allows time-varying for the parameters.