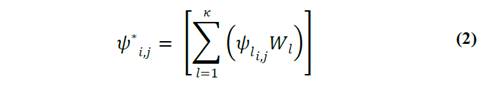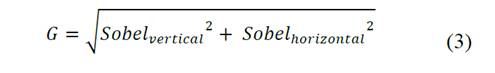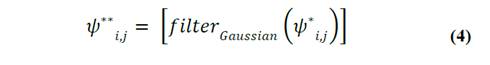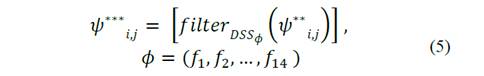1. Introducción
Las técnicas convencionales de clasificación de imágenes toman en cuenta únicamente la información espectral. En algunos casos, también se pueden incluir aspectos geométricos basados en fundamentos matemáticos estadísticos, probabilísticos y de grafos. Sin embargo, dichas técnicas no soportan de manera consistente las características topológicas que definen en dónde comienza y termina cada objeto. Algunos autores han propuesto soluciones a dicho problema usando la teoría de los grafos a partir de la definición de vecindarios 4-conectados y 8-conectados [1]. Desafortunadamente, estos grafos de vecindad presentan problemas o paradojas de conectividad entre sus elementos [2-5].
El propósito de este artículo es proponer un modelo de clasificación de imágenes multiespectrales que toma en cuenta, además de los rasgos espectrales, los rasgos geométricos y de textura. Lo nuevo de este modelo es que usa una representación del espacio libre de las paradojas propias de la representación convencional basada únicamente en píxeles [5]. En contraste con esa representación convencional, Kovalevsky [6] propone el desarrollo de un espacio topológico localmente finito compuesto por complejos de células abstractas el cual permite definir las nociones de adyacencia, conectividad y frontera, proporcionando un espacio con la propiedad de separación 𝑇 0 [7] libre de paradojas. Así mismo, Khalimsky [8] propone un espacio conectado ordenado topológico (COTS por su sigla en inglés) demostrado por Kiselman [2]; sin embargo, la ausencia de dimensión en la representación de cada uno de los elementos del conjunto y su relación directa de este concepto en la definición de adyacencia no permite la definición de vecindarios entre elementos que tienen diferentes dimensiones.
Este artículo presenta un modelo para clasificación de imágenes usando complejos de células abstractas con base en complejos cartesianos y compara su desempeño con un método de clasificación de imagen que emplea la representación convencional del espacio basada en píxeles. El modelo propuesto se compone de seis fases. La primera fase corresponde al constructor del espacio complejo cartesiano (CC), en el cual se transforma la imagen de entrada al espacio de los complejos cartesianos (Fig. 1). En la segunda fase, el espacio CC multiespectral se convierte a uno monocromático a partir de la ponderación de cada una de las bandas de la imagen en función de su matriz de varianza-covarianza.
Fuente: Elaborado por los autores.
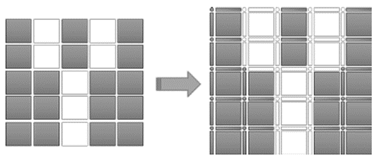
Figura 1 Espacio complejo cartesiano obtenido a partir de la imagen en blanco y negro. Los elementos interpíxel (derecha) 0-dimensionales son representados como puntos y los 1-dimensionales como segmentos de línea horizontal o vertical.
En la tercera fase, usando como base el espacio monocromático, se realiza la detección de los bordes de los objetos a partir del gradiente de Sobel [9], pero centrado en elementos interpíxel 1-dimensionales. El trazado de los límites de los super-píxeles se obtiene a partir del gradiente anterior, aplicando la transformada de cuenca en el espacio de los complejos cartesianos también sobre los elementos interpíxel 1-dimensionales (células-1D).
La cuarta fase, correspondiente a la generación del espacio de textura, busca obtener un espacio complejo cartesiano cuyas células-1D contengan información asociada a la textura del objeto que representa en la imagen, para lo cual se propone una serie de filtros orientados [10] ejecutados sobre las células-1D disponibles [11]. En la quinta fase se realiza la clasificación de los super-píxeles usando máquinas de soporte vectorial [12] (SVM por su sigla en inglés), tomando en cuenta además de la respuesta espectral también la textura. Finalmente, en la sexta fase, se realiza la evaluación de exactitud de la clasificación obtenida usando el nuevo enfoque.
En [13] se presenta un trabajo similar en el cual se realiza una comparación de los resultados de la clasificación basada en píxeles con respecto a la basada en super-píxeles usando, en los dos casos, como representación del espacio a los complejos cartesianos. Sin embargo, en dicho trabajo, la estimación de la probabilidad de límite con base en el cálculo del gradiente multiespectral y de textura implementado no proporciona una mejora significativa en los resultados. Adicionalmente, para la obtención de la imagen de niveles de gris se realiza una suma promediada.
En contraste, en el presente artículo se realiza la comparación de los resultados entre una clasificación obtenida usando una representación convencional del espacio y otra clasificación basada en un espacio representado como un complejo cartesiano que toma como base el gradiente de Sobel [14-16]. Adicionalmente, para la obtención de la imagen de niveles de gris se introduce un procedimiento basado en la matriz de varianza/covarianza de la imagen multiespectral.
El resto del artículo está organizado de la siguiente manera. En la sección 2 se presenta la descripción de los datos experimentales, en la sección 3 se describe el método utilizado, en la sección 4 se presentan y discuten los resultados y en la sección 5 se presentan las conclusiones.
2. Datos
En este trabajo se usó como insumo principal una imagen proporcionada por la Sociedad Internacional de Fotogrametría y Percepción Remota (ISPRS por su sigla en inglés) [17] correspondiente a la localidad de Vaihingen (Alemania), que también se usó en [13]. La imagen es una ortofoto aérea, con resolución espacial de 8 cm y resolución radiométrica de 8 bits, tomada en el año 2008, que incluye las bandas correspondientes al infrarrojo cercano, rojo y verde. En los experimentos de este estudio, a partir de la hoja 11 del conjunto de datos, se seleccionaron dos sub ventanas de tamaño de 1000 x 1000 no sobrepuestas, correspondientes a las coordenadas de archivo (c=400, f=400) a (c=1400, f=1400) para la creación del modelo y (c=893, f=1400) a (c=1983, f=2400) para evaluación de exactitud (Fig. 2).

Fuente: Elaborado por los autores.
Figura 2 Imágenes usadas en la creación del modelo (izquierda) y validación (derecha). Las escenas corresponden a una composición en falso color infrarrojo. 1 cm en la imagen equivale a 20 m en el terreno.
La clasificación de referencia, realizada manualmente por ISPRS, comprende las siguientes categorías de cobertura del suelo urbano: Edificio, Vegetación Baja, Árbol, Carro y Superficie Impermeable.
3. Método
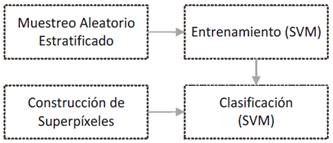
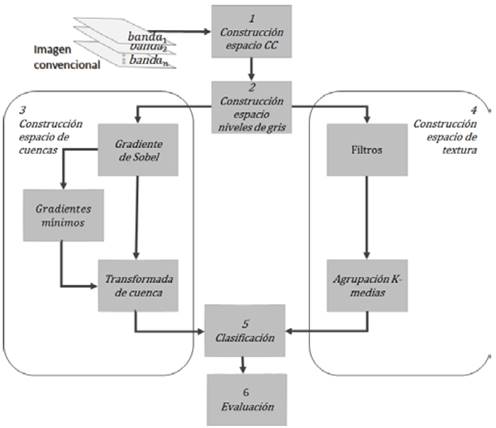
Teniendo en cuenta que el propósito principal de esta investigación es evaluar el aporte de rasgos geométricos extraídos a partir de relaciones topológicas no ambiguas proporcionadas por los complejos cartesianos, el modelo de clasificación propuesto toma como línea base un flujo de procesos (Fig. 3) que simplifica el trabajo expuesto en [10].
Fuente: Elaborado por los autores.
Figura 3 Flujo de procesos de la clasificación basada en complejos de células abstractas.
En la primera fase del modelo, la imagen convencional de entrada es convertida al espacio de representación de los complejos cartesianos empleando la implementación propuesta en [11]. En la segunda fase, se lleva a cabo la transformación de la imagen a niveles de gris involucrando todas las bandas espectrales del espacio original para obtener el valor único radiométrico que es empleado en las fases siguientes. La tercera fase de generación del espacio de cuencas tiene como propósito resaltar los bordes de los elementos inmersos en la imagen procesada y a partir de ellos obtener los límites de cuenca; para lograr este objetivo, en el modelo se plantea un bloque de procesamiento sobre el espacio complejo cartesiano de niveles de grises basado en el gradiente de Sobel [9] empleando el procedimiento descrito en [13]. Posteriormente, se procede a calcular el espacio de cuencas, cuyo objetivo final es la obtención de los polígonos que definen a los super-píxeles de la imagen. La implementación de la transformada de cuenca en el espacio de los complejos cartesianos se realiza a partir de las células-1D las cuales se someten a un proceso de expansión con base en un vecindario libre de paradojas de conexión y cuyo resultado final traza límites de cuenca no ambiguos aprovechando la topología 𝑇 0 disponible en los espacios localmente finitos proporcionados por los complejos cartesianos.
La cuarta fase se encarga de la generación del espacio de textura obteniendo como resultado un espacio complejo cartesiano cuyas células unidimensionales contienen la información asociada a la textura del objeto que representa en la imagen. Esto se realiza a partir de la aplicación inicial de una serie de filtros orientados sobre las células-1D del espacio complejo cartesiano de la manera propuesta en [10], pero sobre elementos inter-pixel unidimensionales como se propone en [11]. El propósito de esta fase es permitir que la máquina clasificadora incluya en sus criterios de clasificación no solo la respuesta espectral del espacio original, sino, además la posible pertenencia de ese elemento a una misma textura. En la fase 5 se lleva a cabo la clasificación de la imagen usando la técnica SVM y, en la fase 6, se realiza la evaluación de exactitud de la clasificación obtenida.
A continuación, en las secciones 3.1 a 3.4, se especifican los aportes realizados por la presente investigación sobre el espacio complejo cartesiano para las fases 1, 2, 3 y 4. En la sección 3.5 se incluye una descripción de la forma en que las capas de super-pixeles y de textura fueron generadas a partir de la representación convencional de la imagen. En la sección 3.6, se describe la fase de clasificación mientras que la fase de evaluación es descrita en la sección 3.7.
3.1. Construcción del espacio complejo cartesiano
La representación de la imagen se realizó mediante un complejo cartesiano bidimensional. Cada píxel de la representación convencional del espacio corresponde con una célula-2D. Para la definición de los elementos interpíxel, células-0D y células-1D, se adoptó lo establecido en [6] realizando una implementación propia de la regla de asignación EquNaLi. En la Fig. 1 se muestra la asignación de etiqueta para una imagen sintética en blanco y negro (255 y 0 respectivamente) de 5 𝑋 5.
3.2. Construcción del espacio de niveles de grises
Para la obtención de la imagen de niveles de gris se realizó la combinación de las bandas espectrales originales cuantificando el nivel de información aportado por cada una con base en la matriz de varianza / covarianza [12]. El aporte o peso de cada banda l se determina por medio de la ec. (1).
en donde 𝐶 𝑞,𝑙 corresponde a cada elemento de la matriz de varianza / covarianza y 𝜅 al número de bandas de la imagen.
A partir del vector de pesos 𝑊 𝑙 se procede a calcular el valor de nivel de gris de cada célula-2D del espacio complejo cartesiano, para lo cual se aplica la ec. (2).
en donde 𝜓 es el vector de valores asociado a la célula-2D con coordenada (𝑖,𝑗) en el espacio complejo cartesiano inicial.
3.3. Construcción del espacio de cuencas
Para obtener los polígonos que describen las formas de los objetos presentes en la imagen se implementó y aplicó la transformada de cuenca al espacio complejo cartesiano. La detección de bordes se realizó mediante la técnica de Sobel [14-16] aplicando a cada célula-1D del espacio de niveles de gris la función de filtro 𝑓𝑖𝑙𝑡𝑒𝑟 𝑆𝑜𝑏𝑒𝑙 con base en la respectiva máscara de filtrado según la orientación de la célula-1D [13]. La imagen de gradiente [16] final fue calculada para cada célula-2D de acuerdo con la ec. (3) a partir del valor de Sobel de las dos células-1D disponibles (una vertical y la otra horizontal) en el espacio para una célula-2D, con base en la relación de dependencia de células propias interpíxel [6,18].
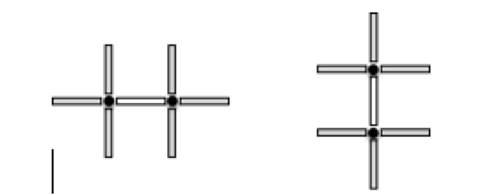
Para la ejecución del algoritmo de cuenca geográfica se utilizó como elemento central una célula-1D en la definición de un nuevo vecindario. La célula1D central se conecta con sus 6 células-1D vecinas más cercanas a través de las células-0D que la limitan, tal y como se muestra en la Fig. 4, en la cual, cada segmento de recta corresponde a una célula-1D y cada punto a una célula-0D que permite conectar a la célula-1D central con sus seis células-1D vecinas.
Fuente: Elaborado por los autores.
Figura 4 Definición del vecindario horizontal (izquierda) y vertical (derecha) centrado en una célula-1D.
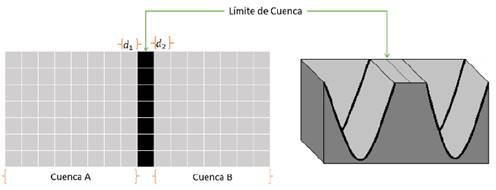
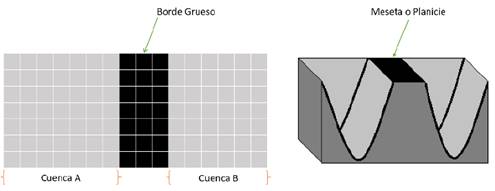
Debido a que la transformada de cuenca se basa en el fenómeno físico de inundación, es posible que se presente el inconveniente de meseta o planicie de la imagen [19] (Fig. 5). Para tratar con este problema se desarrolló un método simplificado aplicando el adelgazamiento en función de la distancia más corta del centro del borde hacia la cuenca más cercana. La Fig. 6 ilustra este proceso, en donde 𝑑 1 y 𝑑 2 representan las distancias desde el centro de borde hasta la cuenca A y B respectivamente.
Fuente: Elaborado por los autores.
Figura 5 Meseta de cuenca en representación digital (izquierda) y en relieve (derecha).
3.4. Construcción del espacio de textura
3.4.1. Filtrado
Tomando como base el espacio complejo cartesiano de niveles de gris, el espacio filtrado tiene como propósito resaltar los contornos o límites de los objetos presentes en la escena. Para ello, tomando en cuenta la definición de segmento de línea recta digital (DSS por su sigla en inglés) [18] y lo propuesto en [11], se definieron 7 orientaciones, cada una con dos direcciones sobre un semiplano digital, con lo cual se obtienen 14 máscaras de filtrado. Dado que la curva de contorno está definida sobre las células-1D, el elemento central de nuestra máscara digital será una célula-1D. Debido a que la escena digitalizada puede presentar ruido, se aplica al espacio de niveles de gris una máscara de supresión de ruido con el propósito de eliminar los pequeños elementos que puedan dar lugar a falsas texturas con base en la ec. (4).
en donde 𝜓 ∗ es el valor de nivel de gris de la célula-2D con coordenada (𝑖,𝑗) en el espacio complejo cartesiano inicial.
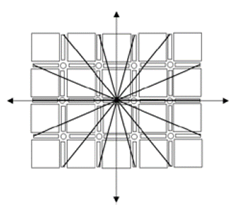
La Fig. 7 muestra las 14 orientaciones desde la célula-1D central que se buscan resolver por medio de segmentos DSS dentro de la máscara.
Fuente: Elaborado por los autores.
Figura 7 Sección digital con una célula-1D horizontal como elemento central del conjunto con las orientaciones para las máscaras de filtrado.
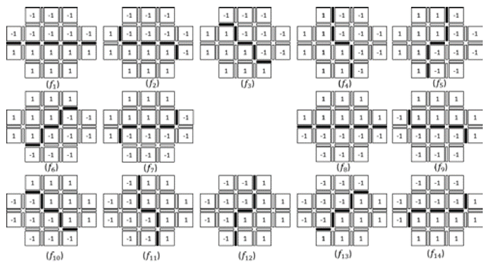
Para obtener cada una de las orientaciones requeridas, la máscara es dividida en dos partes simétricas a la célula-1D central para cada una de las dos orientaciones a lo largo de la DSS que cruza la célula-1D central. La información radiométrica se encuentra en cada célula-2D del espacio complejo cartesiano, razón por la cual, la matriz de filtrado estará compuesta por cada célula-2D del vecindario más pequeño de la célula-1D sobre la cual se define cada DSS. La Fig. 8 muestra la asignación de los coeficientes de un núcleo balanceado en una matriz de filtrado direccional.
Fuente: Elaborado por los autores.
Figura 8 Definición de núcleos de filtrado balanceado incluyendo ambas orientaciones de cada DSS.
Una vez definidas las máscaras de filtrado, se construyó el espacio filtrado, formado por el conjunto de células-1D cuyo vector de valores corresponde al resultado de la máscara de filtrado aplicada al espacio de niveles de gris de acuerdo con la ec. (5).
Donde 𝑓𝑖𝑙𝑡𝑒𝑟 𝐷𝑆𝑆 𝜙 corresponde a la función de filtrado direccional en la dirección 𝜙.
3.4.2. Espacio de Textura
Aplicando la estrategia propuesta en [20], la cual consiste en detectar, localizar y agrupar elementos que se repiten en una imagen, se aplicó al espacio filtrado la técnica de agrupamiento 𝑘-medias [21], cuyo algoritmo, destinado a situaciones en las cuales todas las variables son de tipo cuantitativo, utiliza el cálculo de la distancia cuadrática euclidiana entre cada una de las muestras del conjunto. El resultado final son los vectores de valores más característicos del espacio filtrado que representan las clases de textura en la imagen [20], lo cual da lugar a un nuevo espacio que tiene por nombre espacio de textura. Para la implementación del algoritmo de 𝑘-medias, los centros de clase inicial fueron distribuidos a lo largo de los valores máximos y mínimos de cada valor del vector de valores asociado a las células-1D. Se definieron tantos centros como el número de grupos dado.
El propósito de distribuir los centroides iniciales a lo largo de un vector entre los valores más distantes, fue propiciar una mayor convergencia a lo largo de las iteraciones del algoritmo de 𝑘-medias. Con el conjunto de centroides iniciales 𝜍= 𝜍 1 ,…, 𝜍 𝜉 definido, se procedió al proceso iterativo de cálculo de distancias y a la reasignación de centros de grupo y membresía a los mismos.
3.5. Modelo en el espacio convencional de píxeles
Con el propósito de permitir una evaluación comparable de los resultados, el flujo de procesos mostrado en la Fig. 3 se implementó también para la representación convencional de la imagen aplicando procedimientos equivalentes usando Matlab®. Para la construcción del espacio de textura se diseñaron máscaras de filtrado de 5×5 píxeles (Fig. 9) con un número de direcciones cercano a las definidas para el espacio de los complejos cartesianos aplicando el principio de filtro direccional derivativo [22]. La construcción del espacio de textura convencional se realizó también por agrupamiento k-medias pero tomando como elemento de procesamiento el píxel central.

Fuente: Elaborado por los autores.
Figura 9 Máscaras de filtrado direccional sobre el espacio de representación convencional.
Para la construcción del espacio de cuencas (super-píxeles) sobre la representación del espacio convencional se aplicaron las dos máscaras de Sobel seguida del cálculo del respectivo gradiente, finalizando con la ejecución de la transformada de cuenca en la herramienta Matlab®, la cual traza los límites de cuencas sobre píxeles que quedan sin valor de etiqueta de cuenca, por lo que se les asigna la moda sobre una máscara de 3×3.
3.6. Espacio de clasificación complejo cartesiano
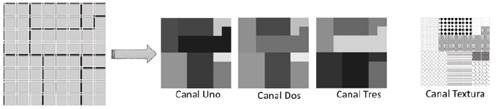
Para la clasificación de la imagen se usó la técnica SVM [12] tomando las bandas espectrales y el canal de textura como variables predictoras y los super-píxeles obtenidos en la construcción del espacio de cuencas como unidad de clasificación. Para el cálculo del descriptor de super-píxel tanto a nivel radiométrico como de textura se tomó el vector de valores medios del grupo de píxeles (células-2D) respectivo (Fig. 10).
Fuente: Elaborado por los autores.
Figura 10 Mapeo de polígonos definidos por el espacio de cuencas a super-píxeles.
La fase de clasificación de imagen se desarrolló de acuerdo con las etapas expuestas en la Fig. 11, las cuales son empleadas en cada uno de los escenarios que se describen en la sección 3.7.
El muestreo aleatorio estratificado se realizó sobre los píxeles de la sub-ventana de entrenamiento y no con base en super-píxeles ya que, por un lado, ésta corresponde a un área distinta de la sub-ventana empleada durante la fase de clasificación; y por otro, en el entrenamiento solo se considera el espacio de rasgos. El espacio bidimensional de super-píxeles se transforma a un espacio unidimensional (Fig. 12) de forma que cada uno de los grupos de píxeles correspondientes a un super-píxel es caracterizado por una única unidad de clasificación. El espacio unidimensional expuesto en la Fig. 12 se convierte en la entrada a la máquina SVM clasificadora. Una vez finaliza la clasificación, se realiza el proceso inverso, recuperando el espacio bidimensional original.
3.7. Evaluación
El flujo de procesos presentado en la Fig. 3 fue aplicado al conjunto de datos descrito en la sección 2 tanto para la imagen en su representación convencional de píxeles como para su representación como complejo cartesiano. Durante la fase de clasificación y con el propósito de facilitar la validación del modelo, se diseñaron 3 escenarios en cada uno de los cuales se usaron super-píxeles como unidades a clasificar. La principal razón para ello es la reducción en el número de elementos del espacio que se deben clasificar.
En el escenario No. 1 (Fig. 13) se realizó la clasificación tomando como variables explicativas únicamente las 3 bandas espectrales disponibles. Este escenario permite valorar el efecto que tienen los super-píxeles trazados en el espacio complejo cartesiano basado en las nociones topológicas para los espacios 𝑇 0 , en comparación con los super-píxeles trazados a partir del espacio de representación convencional el cual no incluye estas nociones topológicas.

Fuente: Elaborado por los autores.
Figura 13 Escenario de clasificación No.1 tomando como variables explicativas únicamente los rasgos espectrales.
En el escenario No. 2 (Fig. 14) se realizó la clasificación tomando como variable explicativa únicamente la imagen de textura. Este escenario permite evaluar la calidad de la capa de textura obtenida en el espacio de los complejos cartesianos en comparación con la obtenida en el espacio de representación convencional.

Fuente: Elaborado por los autores.
Figura 14 Escenario de clasificación No. 2 tomando como variable explicativa únicamente el rasgo de textura.
Finalmente, en el escenario No. 3 (Fig. 15) se realizó la clasificación tomando como variables explicativas las 3 bandas espectrales disponibles y la imagen de textura. Este escenario permite evaluar el aporte que entrega la capa de textura a la clasificación al ser incluida como banda adicional.

Fuente: Elaborado por los autores.
Figura 15 Escenario de clasificación No. 3 tomando como variables explicativas los rasgos espectrales y la banda de textura.
En la evaluación de resultados se hizo uso de métricas que tradicionalmente se usan para medir la exactitud temática en estudios de clasificación basados en píxeles, tales como la matriz de confusión, el índice kappa [12] y los intervalos de confianza [23] asociados. Es importante mencionar que existen métricas de exactitud basadas en objetos que pueden ser apropiadas en aplicaciones específicas [24].
4. Resultados y discusión
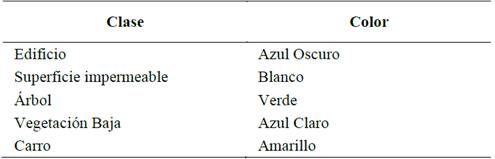
La Fig. 16 muestra la clasificación de referencia que se utilizó tanto para entrenar la máquina SVM (a la izquierda) como para evaluar la exactitud temática de la clasificación realizada (a la derecha). En la Tabla 1 se expone la codificación de color usada por cada clase.
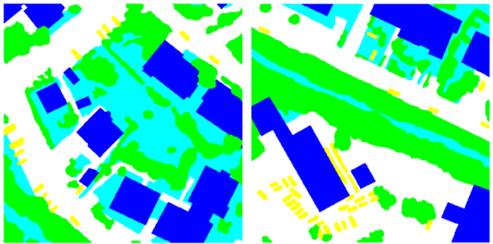
Fuente: Elaborado por los autores.
Figura 16 Clasificación de referencia para entrenamiento (izquierda) y para validación (derecha).
El número de cuencas trazadas en la representación convencional fue de 20134 mientras que en el espacio representado como complejo cartesiano fue de 16618, lo cual redujo el tiempo de ejecución de la clasificación que fue 93.69 segundos en el espacio convencional y 82,82 segundos en el complejo cartesiano para el caso del escenario No. 1.
En la Fig. 17 se muestra el resultado de la clasificación para los super-píxeles tanto en el espacio de representación convencional (izquierda) como en el complejo cartesiano (derecha). El escenario No. 1, basado únicamente en los rasgos espectrales, se muestra en la primera fila. El escenario No. 2, basado únicamente en el rasgo de textura, está en la segunda fila. El escenario No. 3, basado en ambos tipos de rasgos, está en la tercera fila.
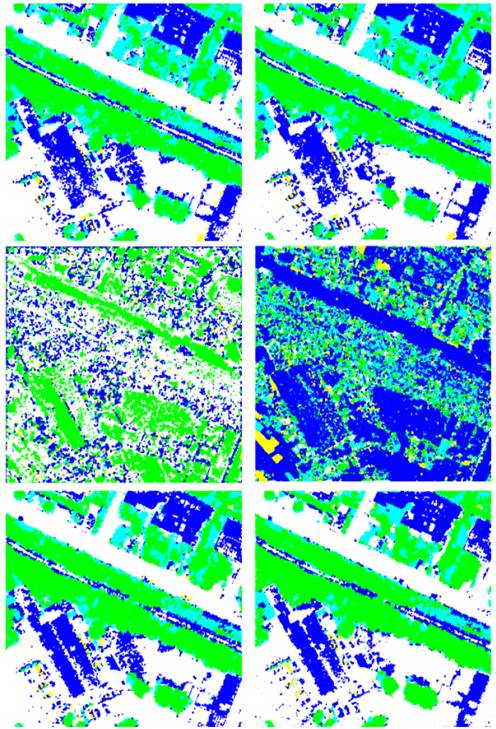
Fuente: Elaborado por los autores.
Figura 17 Clasificación para la imagen representada en el espacio convencional (izquierda) y en el espacio de complejo cartesiano (derecha). En la primera fila se presenta el resultado con base en los rasgos espectrales, en la segunda fila con base en el rasgo de textura y en la última fila con base en ambos rasgos.
La Fig. 18 presenta, para la representación de la imagen en el espacio convencional y para la representación de la imagen como complejo cartesiano, la proporción en la cual cada clase de referencia fue clasificada correctamente mediante la técnica SVM y la proporción en la cual fue incorrectamente clasificada en alguna otra clase. Esta figura resume las respectivas matrices de confusión de los resultados del escenario de clasificación No. 1. En esta figura se puede ver, por ejemplo, que el porcentaje de clasificación correcta de las clases Superficie impermeable y Vegetación Baja obtenido usando el espacio de complejos cartesianos, fue mayor que el obtenido usando el espacio convencional.
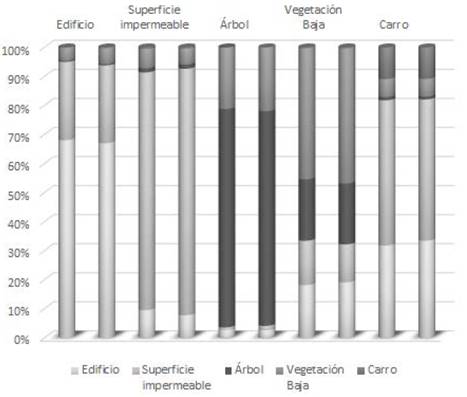
Fuente: Elaborado por los autores.
Figura 18 Confusión ponderada para la clasificación en el espacio convencional y como complejo cartesiano con base en rasgos espectrales (Escenario No. 1). Cada columna muestra de qué manera la clase respectiva (rotulo superior) fue clasificada por el clasificador SVM en cada una de las posibles clases. En cada par de columnas contiguas, la primera columna corresponde al espacio convencional mientras que la segunda representa el complejo cartesiano.
La Fig. 19 presenta, para la representación del especio convencional y como complejo cartesiano, la proporción en la cual cada clase de referencia fue predicha por el clasificador SVM en las diferentes clases. Esta figura resume las respectivas matrices de confusión de los resultados del escenario de clasificación No. 2.
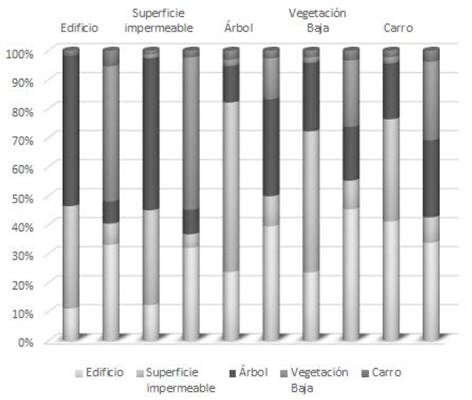
Fuente: Elaborado por los autores.
Figura 19 Confusión ponderada para la clasificación en el espacio convencional y como complejo cartesiano con base en rasgos de textura (Escenario No. 2). Cada columna muestra de qué manera la clase respectiva (rotulo superior) fue clasificada por el clasificador SVM. Para cada par de columnas, la primera corresponde al espacio convencional mientras la segunda al complejo cartesiano.
Los resultados obtenidos en este segundo escenario de clasificación, permitieron evidenciar que, si bien es cierto obtuvo una mejor exactitud general en el caso del espacio representado como complejo cartesiano, este rasgo es insuficiente como único criterio en el proceso de asignación de clase.
La Fig. 20 presenta, para la representación del especio convencional y como complejo cartesiano, la proporción en la cual cada clase de referencia fue predicha por el clasificador SVM en las diferentes clases. Esta figura es un resumen gráfico de las respectivas matrices de confusión de los resultados del escenario de clasificación No. 2 el cual considera conjuntamente los rasgos espectrales y de textura.
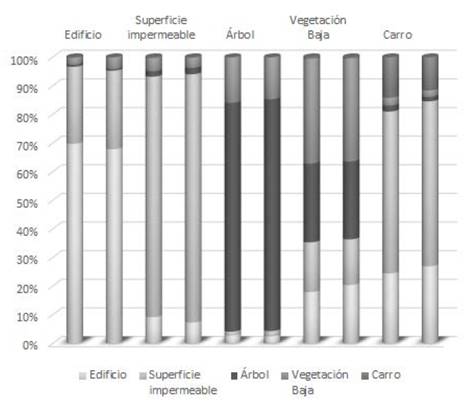
Fuente: Elaborado por los autores.
Figura 20 Confusión ponderada para la clasificación en el espacio convencional y como complejo cartesiano con base en rasgos espectrales y de textura (Escenario No. 3). Cada columna muestra de qué manera la clase respectiva (rotulo superior) fue clasificada por el clasificador SVM. Para cada par de columnas, la primera corresponde al espacio convencional mientras la segunda al complejo cartesiano.
La inclusión del rasgo de textura como criterio adicional de asignación de clase permitió obtener el mejor resultado siendo en este escenario en el cual la exactitud general fue mayor.
Según lo observado en las gráficas de confusión mostradas en las Figs. 18-20, el resultado de la exactitud de la predicción para las clases “Carro”, “Vegetación Baja” y “Edificio” fue menor que la de las clases “Superficie impermeable” y “Árbol”, lo cual evidencia cómo la actual implementación del nuevo enfoque tiende a confundir los elementos de la escena con menor tamaño.
De otro lado, si bien es cierto que la inclusión del rasgo de textura como criterio adicional mejoró la exactitud, en las dos representaciones del espacio, para los tipos de cobertura de mayor tamaño “Superficie impermeable” y “Árbol”, no sucedió lo mismo con las clases restantes. Lo anterior refuerza la idea de que en la consideración del criterio de textura se debe tener en cuenta su dependencia de la escala [20].
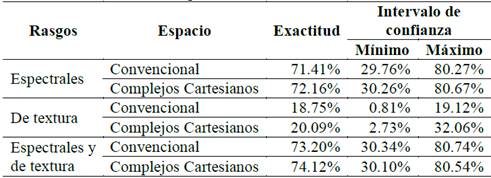
A partir de las matrices de confusión se calculó la exactitud para cada clasificación y sus respectivos intervalos de confianza (ver Tabla 2). En la Fig. 21 se muestra para cada escenario de clasificación los porcentajes de elementos correctamente clasificados.
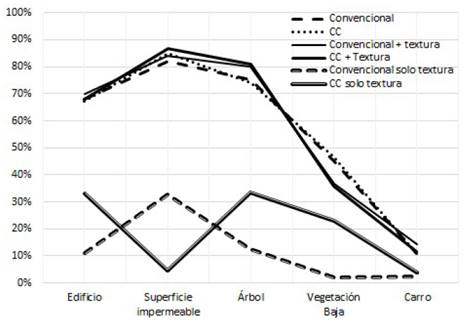
Fuente: Elaborado por los autores.
Figura 21 Porcentaje de elementos correctamente clasificados para cada una de las clases en cada uno de los tres escenarios.
Como se puede apreciar en la Tabla 2 y en la Fig. 21, en los tres escenarios el nivel de exactitud global de la clasificación se mejora levemente cuando se usa el espacio de representación basado en los complejos cartesianos. El mayor valor de exactitud general de la clasificación se obtiene cuando se emplea el rasgo de textura como criterio adicional; sin embargo, este aumento es pequeño con respecto al resultado obtenido de la clasificación con base únicamente en los rasgos espectrales. Esto se explica por el hecho de que la textura es una característica dependiente de la escala [10,20] y por tanto, estos resultados confirman la importancia de evaluar el parámetro de textura a diversas escalas.
5. Conclusiones
Aunque los resultados obtenidos muestran que una representación del espacio basada en los complejos cartesianos permite obtener resultados levemente mejores que una representación convencional, las pruebas de confianza (Tabla 2) muestran que esa mejoría no es estadísticamente significativa. El aumento de la exactitud general obtenida con la clasificación realizada con base en los super-píxeles trazados a partir de los complejos cartesianos con respecto de la obtenida con base en los super-píxeles trazados en el espacio de representación convencional se ve seriamente restringido en el caso de las cuencas de menor tamaño. Ello sugiere que, si se logra construir un espacio de cuencas con super-píxeles que representen con fidelidad el límite de objetos pequeños, debería aumentar la exactitud global de la clasificación.
En contraste con la representación convencional de una imagen, un complejo cartesiano permite desarrollar máscaras de convolución mediante las cuales el resultado es asignado a un elemento 1-dimensional, lo cual es congruente con el hecho de que el patrón que se pretende encontrar obedece a una forma lineal. Ello hace posible desarrollar procedimientos de detección de borde sobre elementos lineales (células-1D) que preservan, sin ambigüedad, las fronteras de los objetos. Las propiedades topológicas dispuestas para los espacios localmente finitos por los complejos cartesianos, pueden beneficiar a otras técnicas de procesamiento de imagen que requieran vecindarios de conexión sin ambigüedades.
De manera general se puede concluir que la clasificación de una imagen multiespectral a partir de un espacio localmente finito definido de manera consistente con los espacios 𝑇 0 permite mejorar el resultado gracias a que durante la creación del espacio de cuencas se incluye la información geométrica definida a partir de vecindarios de conexión correctos topológicamente. Adicionalmente, la inclusión del espacio de textura como un canal adicional de entrada a una clasificación, que se supone permite al algoritmo clasificador tener un nuevo criterio de discernimiento, no mejora significativamente el resultado final de la exactitud general de la clasificación. En una investigación futura, los autores intentarán resolver ese problema mediante la inclusión del aspecto de escala espacial en la definición de los rasgos de textura ya que lo que resulta un grupo de objetos a un nivel de escala específico podría corresponder a un solo objeto con un patrón de textura particular a un nivel de escala menor.