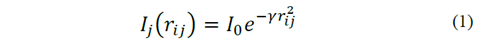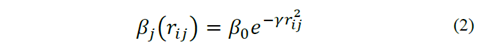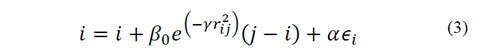1. Introducción
La necesidad de conocer y predecir mutaciones somáticas y realizar distintos estudios relacionados con el desarrollo de los seres vivos es un tópico de relevancia por su impacto en la medicina para detección y tratamiento de patologías, la investigación forense y el desarrollo de medicamentos. Entre los problemas relacionados con el genoma podemos encontrar el estudio del ensamblado de cadenas de ADN (Deoxyribonucleic Acid Fragment Assembly Problem, DNA-FAP), donde dado un conjunto de cientos o miles de fragmentos de ADN, que pueden contener errores, debemos encontrar la secuencia de ADN original a partir de las permutaciones de los fragmentos que mejor representen a dicha secuencia [17].
Existen herramientas que automatizan el secuenciamiento de ADN, entre ellas podemos nombrar PHRAP [13], TIGR assembler [38] y EULER [32] entre muchas otras. Todas estas herramientas están enfocadas a diferentes problemas encontrados durante el ensamblado de fragmentos.
En los últimos años, varios autores han abordado el DNA-FAP con metaheurísticas y algoritmos bioinspirados [26,33]. Las metaheurísticas son procedimientos robustos que encuentran buenos resultados sin tener un conocimiento específico del espacio de búsqueda. Sin embargo, obtener resultados más precisos y en tiempos razonables es aún un tema abierto de investigación. Una de las limitaciones de las técnicas actuales está relacionada con el problema de evaluar grandes secuencias de organismos. De esta manera, si consideramos instancias grandes del DNA-FAP, la evaluación de las soluciones puede requerir varias centenas de minutos. Teniendo en cuenta que además se deben realizar varios cientos de miles de evaluaciones, el tiempo computacional se puede acercar a varios cientos de días. En este contexto, las Unidades de Procesamiento Gráfico (GPU, Graphics Processing Unit) aparecen como una plataforma que provee el poder computacional de cientos de computadoras, lo que permite ejecutar en un tiempo razonable algoritmos que de otra manera serían considerados inviables.
El Algoritmo de Luciérnaga (FA, Firefly Algorithm) fue desarrollado recientemente por Yang [41-45] y desde su aparición se ha utilizado en una variedad de problemas de optimización [3,8,25,40,44]. El FA está basado en el comportamiento de las luciérnagas las cuales están caracterizadas por su capacidad de emitir luz (bioluminiscencia). El FA tiene múltiples ventajas sobre otros algoritmos como los Algoritmos Genéticos (GA, Genetic Algorithms) [10] y los basados en Cúmulos de Partículas (PSO, Particle Swarm Optimizer). Entre ellas podemos mencionar la capacidad de resolver problemas multimodales [43]. Las luciérnagas pueden aleatoriamente subdividirse en sub-grupos y cada grupo puede potencialmente acumularse alrededor de un óptimo local. Todos los óptimos locales, incluido el global pueden ser obtenidos simultáneamente [41-45]. Debido a la reciente aparición de este algoritmo existen pocos trabajos publicados sobre su implementación en GPU [6,15,40].
En particular, en este trabajo extendemos la investigación desarrollada por Vidal y Olivera (2014) [40] y proponemos un Algoritmo de Luciérnaga íntegramente diseñado para GPU con el objetivo de resolver el problema DNA-FAP considerando instancias de distinta complejidad. Para el análisis utilizamos casos de prueba existentes en la literatura [23] con longitudes de hasta 156305 (tamaño de la secuencia de pares base) (1049 fragmentos a recombinar) y comparamos nuestra propuesta con los mejores métodos existentes en la literatura.
En la Sección 2 describimos el Problema del Ensamblado de Fragmentos de ADN. La Sección 3 introduce el Algoritmo de Luciérnaga, una breve explicación sobre la GPU y los detalles de nuestra propuesta. Luego, se describen los parámetros experimentales y una explicación de las instancias a abordar en la Sección 4. La Sección 5 muestra un análisis completo de los resultados obtenidos. Finalmente, en la Sección 6 las conclusiones del trabajo son presentadas.
2. Ensamblado de fragmentos de AND
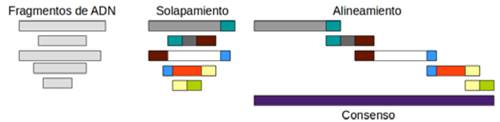
El ADN está compuesto por larguísimas sucesiones de moléculas: Adenine (A), Thynine(T), Guanine (G) y Cytosine (C) llamadas comúnmente bases. Dado lo inmenso de estas cadenas estudiarlas de forma global es casi imposible. Por lo general, las cadenas son copiadas y fragmentadas para ser analizadas, lo que se conoce comúnmente como shotgun. Ésta técnica no mantiene el orden en que fueron fragmentadas ni ninguna otra información. Una vez que estos fragmentos fueron estudiados es necesario volver a la cadena original rearmando de manera inteligente todas las subcadenas. Debido al proceso de copia y corte de las cadenas de ADN los fragmentos pueden contener errores o faltar piezas. Al proceso de rearmado se lo conoce como ensamblado de fragmentos de ADN [17]. Pequeñas secuencias deben ser nuevamente ensambladas en orden solapando porciones de las mismas. La mayoría de los algoritmos de ensamblado realizan los siguientes tres pasos:
Solapamiento ( Overlap ). Consiste en encontrar el mejor solapado entre los sufijos y los prefijos de todos los fragmentos. La práctica común consiste en filtrar pares de fragmentos que no compartan subcadenas significativas.
Alineamiento ( Layout ). Es encontrar el orden en que estaban los fragmentos en la secuencia original. Constituye la parte más costosa del proceso de ensamblado dada la dificultad de decidir si dos fragmentos están solapados (sus diferencias están causadas por errores de copia) o en realidad son dos copias distintas de una repetición. Las subcadenas repetidas son el mayor desafío para ensamblar cadenas de genoma.
Consenso ( Consensus ). Se refiere a derivar la secuencia de ADN a partir de la disposición establecida en el paso anterior.
Para medir la calidad del consenso se observa el llamado cubrimiento ( Coverage ). El cubrimiento de una posición base está definido como el número de fragmentos que comparten esa posición. Esta es una medida de redundancia de un fragmento de dato y denota el número de fragmentos, en promedio, donde un nucleótido se espera que aparezca en el ADN. Esto se calcula como el número de bases leídas por fragmento sobre el tamaño del ADN obtenido. En la Fig. 1 se pueden observar los pasos usuales de las técnicas de ensamblado.
3. Algoritmo de luciérnaga
El Algoritmo de Luciérnaga es una metaheurística desarrollada por Yang [41]. Está inspirada en la imitación de las emisiones de luz utilizada por las luciérnagas para atraerse. Aunque el algoritmo está basado en este fenómeno, en el esquema general propuesto por Yang [41-45] las luciérnagas tienen características particulares:
Todas las luciérnagas son del mismo sexo, por esto una luciérnaga puede ser atraída por cualquier otra.
La atracción es proporcional a su brillo. Por ello para cualquier par de luciérnagas emitiendo luz, la menos brillante se moverá hacía la más brillante (ver Fig. 2.a). A medida que las luciérnagas se alejan la percepción de su luz disminuye. Si ninguna luciérnaga es particularmente más brillante que otra, las mismas se mueven aleatoriamente (ver Fig. 2.b).
La intensidad de la luz emitida por la luciérnaga es afectada o determinada por el valor de la función de aptitud a optimizar.
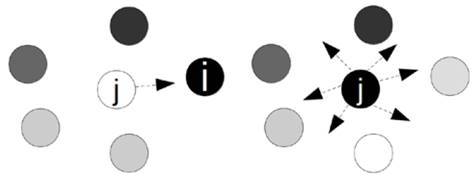
Fuente: Los autores.
Figura 2 Movimiento de las luciérnagas según su atracción: (a) j se mueve hacia i, la luciérnaga más cercana a ella; (b) j tiene más brillo que cualquiera de las otras luciérnagas por lo que se mueve aleatoriamente.
El FA canónico trabaja con dos principios básicos: la variación de la intensidad de la luz I (brillo) y el atractivo β entre dos luciérnagas i y j. En el caso más sencillo para problemas de optimización el brillo I de una luciérnaga localizada en un lugar en particular coincide con su función de aptitud o fitness. La intensidad de la luz se reduce con la distancia a su fuente y la luz es también absorbida por el medio, por esto, el atractivo varia con respecto al grado de absorción de la luz. Para un ambiente en particular con un coeficiente de absorción γ, la intensidad de la luz I varia con la distancia r (ver eq. (1)). Como el atractivo β de una luciérnaga es proporcional a la intensidad de la luz desde el punto de vista de las demás, definimos el β de una luciérnaga a través de la eq. (2).
Donde I 0 es la intensidad de la luz y β0 es el atractivo original de la luciérnaga cuando r = 0. Con respecto al coeficiente de absorción γ, si γ→0 el atractivo de una luciérnaga i coincide con su brillo (aptitud), es decir, el brillo de una luciérnaga no se ve reducido cuando es vista por otra luciérnaga. En el caso de que 𝛾→∞ significa que el valor del atractivo es cercano a cero cuando es vista por otra luciérnaga por lo cual las luciérnagas no se sentirán atraídas por esta y se moverán de manera aleatoria. De esta manera, γ determina la velocidad de convergencia y el comportamiento del algoritmo y β controla el atractivo. Estudios previos indican que valores de 𝛽 0 =1 puede ser utilizado en la mayoría de las aplicaciones [44].
La distancia entre dos luciérnagas i y j ubicadas en diferentes locaciones puede ser expresada por la distancia Euclideana. Teniendo en cuenta r, β e I, el algoritmo es capaz de definir el movimiento de una luciérnaga i con respecto a otra luciérnaga j. El pseudo-código del FA canónico puede observarse en el Algoritmo 1. Primero, la población P de luciérnagas es inicializada (línea 1). Se inicializa la intensidad de la luz para cada luciérnaga i con el valor de aptitud (línea 2). Luego, se define el valor del parámetro γ (línea 3). Mientras la condición de parada no se alcance (línea 4), para cada luciérnaga i, el algoritmo tratará de encontrar una luciérnaga j más brillante, cercana a i (líneas 5 a 13). El algoritmo compara entonces I j e I i , si 𝐼 𝑗 > 𝐼 𝑖 entonces la luciérnaga j se moverá hacía i (línea 8). El movimiento de una luciérnaga i atraída por otra más atractiva j se calcula siguiendo la eq. (3).
Donde el segundo término tiene en cuenta la atracción mientras que el tercero se calcula de forma aleatoria a partir de ϵ i tomando una distribución Gaussiana y 𝛼∈ 0,1 luego la atracción es actualizada (línea 10). Posteriormente, las nuevas soluciones son evaluadas y la intensidad de la luz se actualiza en la línea 11. Las luciérnagas son clasificadas y se encuentra la mejor de ellas (línea 14). Cuando el proceso termina, el Algoritmo 1 retorna los resultados de la ejecución (línea 16).
Como se puede apreciar en el Algoritmo 1 el tiempo de ejecución es 𝑂 𝑛 2 ∗𝑡 donde t es el número de iteraciones del ciclo while. Además, cada luciérnaga debe ser evaluada según la eq. 2, n veces, para cada luciérnaga j. Esta complejidad computacional no es fácilmente posible de reducir.
3.1. Algoritmo de luciérnaga discreto sobre GPU
El Algoritmo de Luciérnaga Discreto (DFA) es una variación del FA canónico utilizado para problemas combinatoriales el cual ha sido exitoso en diversos campos de aplicación [16,22]. El DFA es el modelo base utilizado en el presente trabajo para la implementación sobre GPU. Esta sección presenta nuestra propuesta algorítmica la cual llamaremos GPU-DFA.
3.1.1. Unidades de procesamiento gráfico
Las GPUs se consideran como un coprocesador gráfico de la Unidad Central de Procesamiento (CPU, por sus siglas en inglés). Con este tipo de modelo se busca aliviar la carga computacional de la CPU. Los modelos actuales de GPU suelen tener una gran cantidad de procesadores, los cuales están optimizados para ejecutar una instrucción simple sobre cada elemento de un extenso conjunto de ellos.
Para poder utilizar adecuadamente la capacidad de cómputo de la GPU, NVIDIA ha desarrollado un modelo de programación llamado CUDA (Compute Unified Device Architecture) [30]. CUDA permite a los programadores implementar funciones llamadas kernels. Un kernel contiene la porción de código que será ejecutada en la GPU. Esta función es invocada desde el anfitrión y se despliega en la GPU. CUDA nos da la posibilidad de implementar los kernels usando lenguaje C estándar más algunas extensiones de NVIDIA. Además, nos permite organizar el paralelismo en tres niveles: rejilla, bloque e hilo. Cada vez que se invoca un kernel, se crea una rejilla de bloques, los cuales a su vez agrupan múltiples hilos. Durante la ejecución del kernel, cada hilo tiene acceso a diferentes tipos de memoria dentro de la GPU. Esta jerarquía abarca: registros, memoria local y compartida, memoria global, constante y de texturas. El lector puede consultar en el Manual del Usuario [30] para obtener información más detallada de CUDA.
Existen pocas aproximaciones que utilicen algoritmo de luciérnaga sobre GPU [6,15]. Estos modelos han sido testeados sobre dominios continuos obteniendo buenos resultados con respecto a la ganancia de tiempo.
Nuestra principal motivación al diseñar el DFA acelerado por la GPU es establecer un modelo eficiente que ejecute el procedimiento principal del DFA enteramente en GPU. Los objetivos son: (1) minimizar la transferencia entre CPU y GPU evitando cuellos de botella en la comunicación; (2) abordar problemas de optimización combinatoriales utilizando el modelo de interacción de las luciérnagas sobre una plataforma GPU. La arquitectura CUDA es empleada a fin de explotar al máximo la ejecución en paralelo y el procesamiento intensivo de operaciones aritméticas en las GPUs [30].
3.2. Esquema general de la propuesta
3.2.1. Aproximación del DFA sobre GPUs
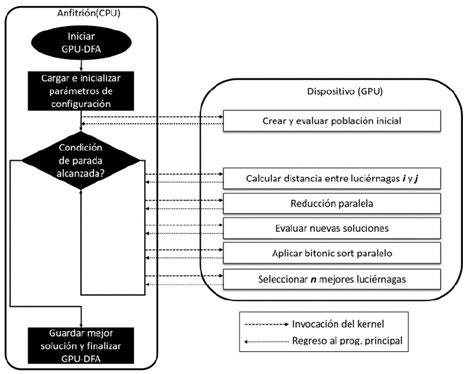
En la Fig. 3 podemos observar un diagrama del GPU-DFA. Al inicio del GPU-DFA todos los parámetros son transferidos a la memoria principal de la GPU. Adaptar este tipo de algoritmo bioinspirado no es una tarea sencilla puesto que la gestión de la memoria en la GPU debe ser cuidadosamente manejada. La transferencia de datos entre CPU y GPU puede producir cuellos de botella y se busca minimizarla en nuestra propuesta. Utilizamos un grupo de kernels donde realizamos las siguientes tareas: primero, el GPU-DFA crea y evalúa cada luciérnaga de la población P usando un hilo (thread) de la GPU para generar cada solución. A continuación, hasta que no se alcance la condición de terminación, el GPU-DFA ejecuta una serie de kernels para evaluar en paralelo si cada luciérnaga i se moverá a otra luciérnaga j y posteriormente generar una población de n mejores luciérnagas. La división en múltiples kernels se debe a la heterogeneidad y complejidad de las tareas. Así, las operaciones costosas son ejecutadas principalmente en la GPU.
El Algoritmo 2 muestra en detalle las operaciones anteriormente mencionadas dentro del esquema del GPU-DFA. Todos los métodos presentados en el Algoritmo 2 intentan explotar al máximo el rápido acceso a los diferentes niveles de memoria de la GPU. Debido a la complejidad de algunas operaciones que son completamente diferentes unas con otras, hemos tratado de escribir kernels simples y pequeños ya que el costo de lanzarlos es insignificante con respecto a las operaciones a realizar y se utilizan menos registros de memoria.
En las siguientes secciones se explica en detalle uno a uno los procedimientos del GPU-DFA.
3.2.2. Inicialización
Durante la inicialización, se asigna un espacio de memoria en la GPU, el cual corresponde a los datos de entrada y las soluciones candidatas. Luego, los datos de entrada iniciales y las estructuras adicionales son copiados a la GPU. Es importante observar que los datos de entrada son solamente de lectura y nunca cambian durante la ejecución. Por esta razón sus valores son copiados por una única vez y al principio durante toda la ejecución. En el GPU-DFA, la inicialización de la población y la evaluación de la aptitud de cada solución son asignadas a cada hilo de la GPU. De esta manera, se busca que cada hilo pueda acceder consecutivamente a la información de la solución buscando lograr un patrón de acceso a memoria coalescente y optimizar el tiempo de acceso a dicha memoria [18].
3.2.3. Cálculo de distancias y operación de reducción
El primer paso evolutivo para el GPU-DFA es calcula r, β e I en paralelo para cada par de luciérnagas i y j. Al evaluar cada combinación es necesario aplicar un método paralelo de reducción para conocer si la solución j necesita moverse de forma aleatoria o debe acercarse a una solución más brillante.
El método de reducción es utilizado para identificar posibles movimientos de cada luciérnaga con respecto a las otras. Al lanzar el kernel, se despliega una serie de bloques, cada uno de ellos asignado al conjunto de datos de una luciérnaga obtenidos en el paso anterior. El GPU-DFA utiliza una estructura auxiliar en la memoria compartida de la GPU. El resultado será la decisión sobre qué movimiento realizará la luciérnaga.
3.2.4. Modificaciones en paralelo
Definido para cada luciérnaga j el movimiento que va a realizar, el GPU-DFA crea y evalúa n*m nuevas soluciones alterando cada una con un operador específico o de forma aleatoria según sea el caso y se almacenan en temp.
3.2.5. Ordenamiento bitonic
El esquema del algoritmo hace necesario ordenar el conjunto temp según su aptitud. Para ello utilizamos el ordenamiento Bitonic paralelo [33] para luego seleccionar las n mejores luciérnagas y actualizar con ellas P. El ordenamiento Bitonic tiene una complejidad de O(n (log n)2). Este método necesita únicamente un número de comparaciones e intercambios de O(n log n). La constante oculta en la notación asintótica es más pequeña que para otros métodos de ordenamiento en paralelo. Este ordenamiento puede ser implementado en paralelo en modernas arquitecturas como las GPUs, sin utilizar ningún acceso de escritura que pueda involucrar a la CPU.
3.2.6. Generación de números aleatorios
El desempeño de un algoritmo bioinspirado depende en gran medida de la calidad del generador de números aleatorios utilizado. Para nuestro trabajo hemos usado un generador aleatorio Mersenne Twister [36]. Al comienzo de la ejecución el GPU-DFA define una semilla global con la cual se inicializa una semilla local en cada hilo. Posteriormente, cada semilla local es invocada continuamente por cada hilo para subsecuentes generaciones de números aleatorios.
3.2.7 Codificación de la solución
La representación juega un rol importante en la eficiencia y eficacia de cualquier algoritmo. Con el objetivo de hacer más eficiente el mapeo entre cada hilo id y solución de P en la GPU se utilizó una representación vectorial. Esta codificación utiliza un alfabeto Σ={1,…,l} donde l es el número total de fragmentos de ADN a ordenar. Entonces, una solución es una permutación de fragmentos de ADN. En su representación cada variable toma su valor del alfabeto Σ.
La disposición de la población en la memoria de la GPU fue cuidadosamente diseñada. La forma de las soluciones basada en cromosoma [20] simplifica el movimiento individual de las mismas en la selección, la comparación y las fases de perturbación como así también en la comunicación anfitrión-dispositivo necesaria para la operación de reemplazo y actualización de las mejores soluciones durante el proceso evolutivo.
4. Configuración de la experimentación
En esta sección se presentan las especificaciones sobre la configuración y parámetros definidos. Primero, se introducen detalles de las instancias seleccionadas del DNA-FAP. Luego, se muestra la metodología y parametrización para la experimentación.
4.1. Instancias
Para nuestro estudio se llevaron a cabo experimentos con diferentes instancias del DNA-FAP [23]. Las mismas se pueden diferenciar en dos grupos, el primero de ellos ha sido generado mediante el uso de GenFrag [7] y para el segundo se ha utilizado el programa DNAgen. La Tabla 1 resume las instancias estudiadas, sus nombres, cubrimiento, tamaño (número de fragmentos por instancia), tamaño de la secuencia original y el óptimo para cada una de ellas. Las instancias están ordenadas por grupo y número de fragmentos.
Tabla 1 Información de los conjuntos de datos utilizados para realizar los experimentos.
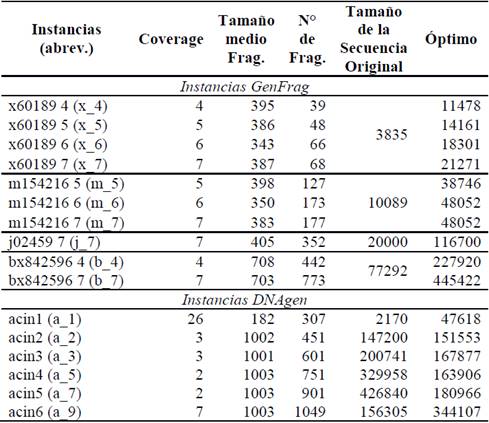
Fuente: [23].
4.2. Valores de los parámetros de experimentación
La distancia entre dos luciérnagas es definida a través de la eq. (4). El parámetro A es el número de arcos diferentes entre i y j. El parámetro l indica el tamaño del problema (número de fragmentos). El valor de r varía dentro del intervalo [0,10] según la eq. (4) (ver [16]).
En este trabajo, el algoritmo utiliza un operador 2-opt que consiste en remover 2 arcos y reemplazarlos con otros 2 arcos para reconectar los fragmentos resultantes de la remoción, y así obtener un secuenciamiento. El operador es aplicado k veces, donde k es un número seleccionado aleatoriamente entre 2 y el parámetro A. Si el movimiento de la luciérnaga es aleatorio, el operador 2-opt es aplicado tomando k un valor cualquiera mayor a 0.
Para la mayoría de los problemas se suele utilizar una población n entre 15 y 100. En particular para el FA el rango ideal es entre 25 a 40 [41,42]. Considerando que los hilos de la GPU están planificados en bloques de 32 es una buena práctica tomar como tamaño de población 32 o múltiplos de 32 [30]. Con el objetivo de testear el GPU-DFA se utilizaron como parámetros del algoritmo n=32 y m=16. Estos valores fueron obtenidos en un estudio previo realizado por los autores y puede ser consultado en [40].
Con la finalidad de hacer una comparación entre las dos implementaciones del DFA (CPU y GPU) se eligió como criterio de terminación alcanzar 1 millón de evaluaciones. Se realizaron 30 ejecuciones independientes para cada instancia. En la Tabla 3 hemos marcado los mejores valores obtenidos con gris oscuro y con gris claro aquellos que son los segundos mejores resultados.
Los experimentos fueron realizados sobre una CPU AMD FX(tm)-8320 Eight-Core Processor con 16GB de RAM. El sistema operativo utilizado fue Ubuntu Precise 12.04. En el caso de la GPU se utilizó una NVIDIA GeForce GTX 780 Ti con 3GB of DRAM y la versión 6.0 de CUDA.
5. Resultados
En esta sección se muestran los resultados de los experimentos realizados. Se ha cuantificado la calidad de las soluciones considerando su valor de aptitud como así también el número de contigs obtenidos para cada instancia. Además, se compararon los tiempos de ejecución para las versiones en CPU y GPU del DFA.
5.1. Análisis numérico
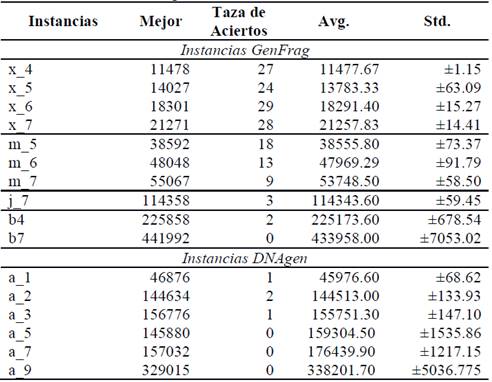
La Tabla 2 indica los resultados del GPU-DFA para todas las instancias mencionadas en la Sección 4. La primera columna corresponde con el nombre abreviado para cada instancia.
La columna dos muestra el mejor valor de aptitud obtenido y la tercera columna la taza de acierto, definida como el porcentaje de ejecuciones en las que se alcanzó el óptimo conocido, en las 30 ejecuciones. Las columnas cuatro y cinco indican el valor de aptitud promedio (Avg.) con su correspondiente desviación estándar (Std.) para las 30 ejecuciones. El GPU-DFA obtiene valores de aptitud iguales al óptimo o muy cercanos a éste. En particular, el algoritmo obtiene el óptimo para 11 de las 16 instancias al menos una vez. Para el grupo de las instancias b_7, a_5, a_7 y a_9 el GPU-DFA no alcanza la solución óptima, sin embargo, las soluciones obtenidas son competitivas y cercanas al óptimo en general. Estos resultados indican que el GPU-DFA es capaz de explorar el espacio de búsqueda de manera efectiva mostrando un comportamiento promisorio.
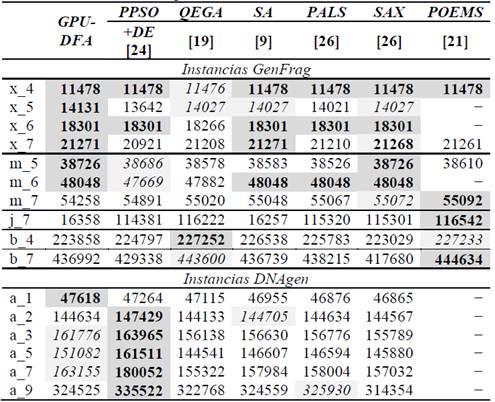
La Tabla 3 compara los resultados del GPU-DFA en contraposición con otros algoritmos. Estos algoritmos son Optimización por Cúmulo de Partículas (Particle Swarm Optimization) y Evolución Diferencial (Differential Evolution) (PPSO+DE) [24], Algoritmo Evolutivo Reina de Abejas basado en un Algoritmo Genético (Queen Bee Evolution Based on Genetic Algorithm, QEGA) [19], Recocido Simulado (Simulated Annealing, SA) [9], Búsqueda local Consciente (Problem Aware Local Search, PALS), SAX [26] y la Optimización de Prototipos con Mejora de Pasos Evolutivos (Prototype Optimization with Evolved Improvement Steps, POEMS) [21]. Se puede observar que la inicialización de forma inteligente en las soluciones candidatas resulta en un beneficio en el proceso de búsqueda, obteniendo estos algoritmos resultados competitivos para todas las instancias.
En general, el GPU-DFA obtiene soluciones competitivas para todas las instancias. Si bien, en algunas de ellas no se llega a alcanzar el óptimo, se logra encontrar el segundo mejor valor superando a las otras metaheurísticas presentadas. Los resultados demuestran que el DFA propuesto optimiza la función de aptitud en las 16 instancias. En particular, se puede observar que en las instancias DNAAgen los algoritmos PPSO+DE y SA superan al GPU-DFA. En el caso de las instancias de pocos fragmentos la mayoría de los algoritmos obtienen resultados similares.
5.2. Comparación de contigs
En esta sección se presenta una comparación entre nuestra propuesta y otros algoritmos ensambladores enfocada en la calidad de las soluciones devueltas. Este análisis se enfoca en la calidad de contigs obtenidos. El cálculo del contig asegura que la mejor solución obtenida representa una secuencia continua.
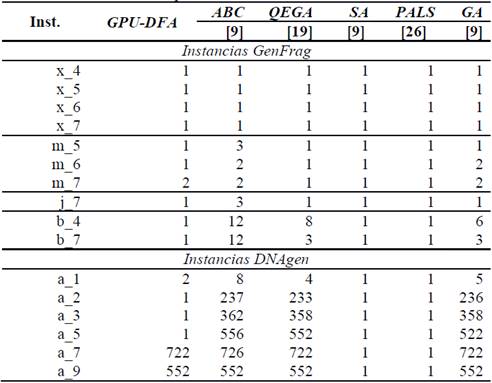
La Tabla 4 presenta los valores contigs de todas las instancias para cada algoritmo. La columna uno muestra el nombre abreviado de la instancia. Desde la columna dos a la columna siete se muestran los valores contigs de los siguientes algoritmos: GPU-DFA, Colonia de Abejas Artificiales (Artificial Bee Colony, [9]), QEGA, SA, PALS y GA [9].
De la Tabla 4 podemos concluir que los algoritmos que poseen algún método inteligente o de búsqueda local obtienen un mejor valor (un número de contigs pequeño). Para GPU-DFA y, en particular, para las instancias m_7, a_7 y a_9 las secuencias reportadas por el GPU-DFA no mejoran los resultados obtenidos por PALS y SA. A diferencia de las técnicas con las que comparamos nuestra propuesta al GPU-DFA no se le ha dotado de ningún operador específico sobre el problema y, aun así, el algoritmo logra resultados equiparables a los existentes en la literatura.
Podemos establecer que el rendimiento observado del GPU-DFA indica que éste es capaz de generar soluciones que alcanzan el óptimo o quedan muy cercanas al óptimo. De la misma forma se observa que el GPU-DFA puede explorar el espacio de búsqueda de forma efectiva, por lo cual es capaz de identificar la región donde se encuentra localizado el óptimo.
5.3. Análisis de tiempo de ejecución
En la Tabla 5 se muestra el tiempo promedio consumido en segundos para las versiones en CPU y en GPU del DFA. En la primera columna se informa el nombre abreviado de cada instancia. La columna dos y tres indican los tiempos de ejecución promedio consumidos por el CPU-DFA y el GPU-DFA respectivamente. Finalmente, la columna cuatro muestra la ganancia de tiempo obtenida.
Tabla 5 Tiempo medio en segundos para encontrar la solución óptima para cada implementación y cada instancia.
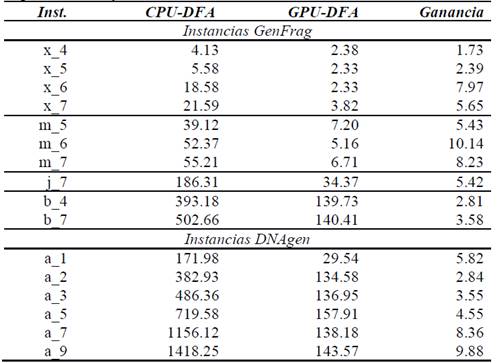
Fuente: Los autores.
Con respecto a la ganancia obtenida, ésta métrica se calculó dividiendo el tiempo promedio consumido por el CPU-DFA sobre el tiempo promedio consumido por el GPU-DFA. Los valores obtenidos que se encuentran por arriba del 1.00 indican que la CPU consume más tiempo que la GPU.
De la Tabla 5 podemos concluir que aun cuando el tamaño de las instancias crezca, el tiempo del GPU-DFA no lo hace significativamente en contraste con el tiempo del CPU-DFA. Esto puede deberse a las características intrínsecas del DFA el cual posee un alto grado de paralelización que maximiza la eficiencia de cada hilo de ejecución manteniendo la simplicidad en cada kernel. La ganancia de tiempo se encuentra entre los valores 1.73 a 10.14, lo que demuestra la capacidad del GPU-DFA para acelerar procesos de ensamblado de ADN.
6. Conclusiones y trabajo futuro
En este trabajo proponemos un Algoritmo de Luciérnaga Discreto implementado sobre Unidades de Procesamiento Gráfico (GPU-DFA) para el Problema del Secuenciamiento de Cadenas de ADN (DNA-FAP). La principal ventaja del Algoritmo de la Luciérnaga frente a otros algoritmos bioinspirados es su capacidad de dividir la población de soluciones en forma automática y de enfrentarse a problemas multimodales.
Se realizaron experimentos sobre el GPU-DFA para analizar su comportamiento. Se ha evaluado la calidad de las soluciones obtenidas y el tiempo de ejecución del algoritmo. Por otro lado, se evaluó la capacidad del GPU-DFA para reensamblar de manera satisfactoria los fragmentos de distintos conjuntos de instancias.
Primero se compararon los valores de aptitud del GPU-DFA en contraposición con otros algoritmos populares en la literatura. Se observó que el GPU-DFA solo era superado por aquellos que poseen una inicialización inteligente de la población inicial para las instancias de mayor cantidad de fragmentos. Luego se analizó la forma de las soluciones obtenidas con respecto a la cantidad de contigs que generaban los algoritmos. El GPU-DFA obtuvo nuevamente resultados promisorios para todas las instancias.
Por último, se realizó una comparación entre la versión en CPU del DFA y nuestro GPU-DFA. La ganancia de tiempo reporta valores entre 1.73 a 10.14 lo que demuestra la capacidad de aceleración de nuestra aproximación al no tener un crecimiento del tiempo de forma lineal para instancias grandes del DNA-FAP en contraposición con la versión en CPU. El método propuesto logró disminuir en hasta 10 veces el tiempo de ejecución del modelo secuencial, lo que permitirá trabajar grupos de fragmentos de mayor magnitud en un tiempo razonable. Por todo esto el GPU-DFA constituye una alternativa atractiva para la resolución de instancias grandes del DNA-FAP.
Como trabajo futuro se espera realizar una hibridación del FA que permita abordar de forma inteligente el DNA-FAP y mejorar así la búsqueda de soluciones.