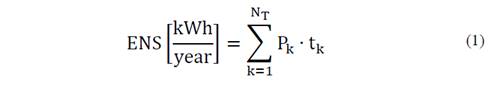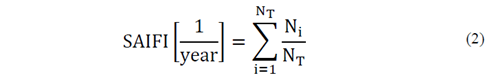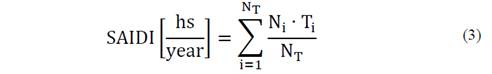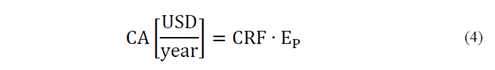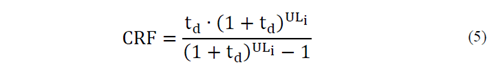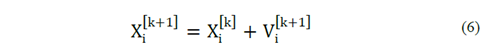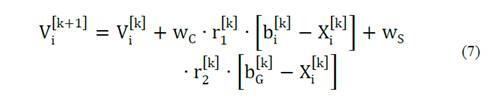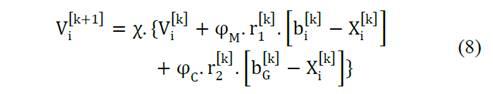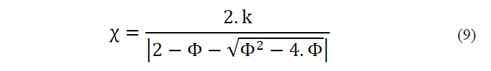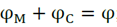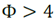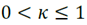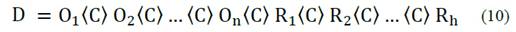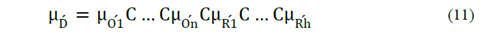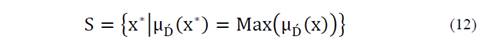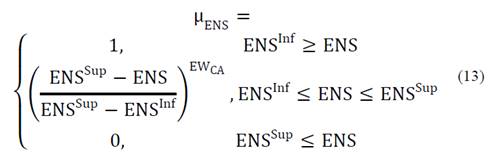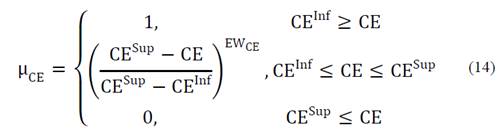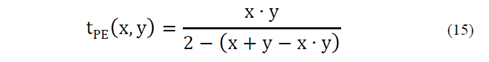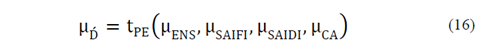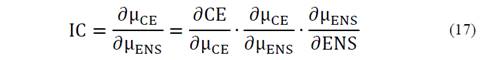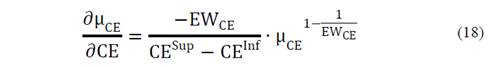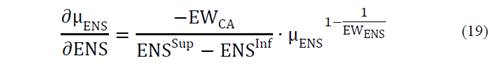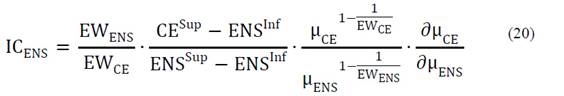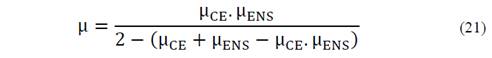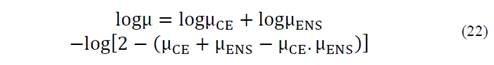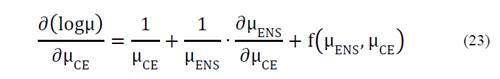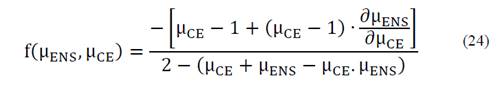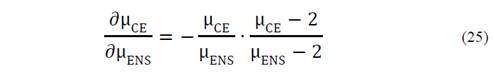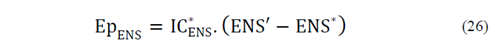1. Introducción
In the next few years after the reform resulting from the segmentation of the Argentine electricity market, a discussion and regulation of the technical criteria to be applied in order to obtain an 'acceptable' quality of service was urgently required. Among the discussion criteria, which is actually regulated and penalized in the Medium Voltage Power Distribution Systems (MVPDS), is the reliability index known as Energy Not Supplied (ENS), which refers to the unavailability of electricity service due to contingencies. In most cases, this may be due to failures in the constructive elements, climatic factors, overloads, etc. In this context there are different reasons for discussion regarding the criteria to be applied by a regulator. In the first place, the network service constitutes a natural monopoly that is not contestable and, consequently, subject to regulation. Second, there is no agreement of criteria to determine whether a decision unit is efficient based on its reliability and technical efficiency indexes. These attributes are "not monetizable", since they are not subject to conventional market equilibrium laws, and therefore there is no agreement on their economic value. Thirdly, the methods used today are based on simplifying assumptions such as linearization of objective function and constraints, use of stochastic models, and so on. The objective of the present work is to establish a formal procedure in order to determine a short-term investment plan, the optimal scenario in terms of the MVPDS Quality of Service. It also aims at reducing investment costs and ENS by Faults in the Medium Voltage lines, guaranteeing the satisfaction of the greatest possible energy demand.
This work is organized as follows: in section 2, the problem of reliability in medium-voltage electrical distribution systems is presented. Secondly, the principles of the Particle Swarm Optimization with Constriction Factor (CF PSO) metaheuristic is described. In third place, the extension to fuzzy domain is proposed for solving multi-objective optimization problems, by means of a fuzzy fitness function. In section 3, a simulation on a real distribution system and the results are presented. The conclusions are described in section 4.
2. Materials and methods
2.1. State of the art: problem, mathematical modeling and solution
The objective of engineering is to solve problems in a technically feasible manner and at a minimum cost. One of the problems in electrical engineering is the problem called reliability. The reliability problem of Medium Voltage Power Distribution Systems (MVPDS) is highly complex to study, model and solve.
MVPDS are vulnerable to being affected by various faults: technical defects in their components, climatic factors, variation in the consumption of users, etc., which produce different types of short circuits or overloads.
In the state of the art, to study the effect of a failure in some node of the electric network, stochastic models such as the Markov chain are used. In probability theory, a Markov model is a stochastic model used to model randomly changing systems. It is assumed that future states depend only on the current state, not on the events that occurred before it [1-2]. For reasons of space and complexity, this topic does not develop more deeply.
The present article continues a research line followed by the authors, in the area of MVPDS, Soft Computing and Artificial Intelligence. Then, different aspects would be considered: the problem studied, its mathematical modeling, its extension to the fuzzy domain and the solution method.
The problem: the Sectioning/Protection (SP) Devices considered in this work were: Interrupters, Disconnectors, and Fuses which have different technical characteristics and costs. The combination of these devices has a different effect on the network and an associated cost. This effect is related to the maneuvers of repair and reestablishment of the service. Using the 'what if' clause, four predominant cases were obtained.
Mathematical modeling: a multiobjective model was extended to the fuzzy domain, by means of the convergence of the different optimization criteria by the t-norm called Einstein Product, according to the 'Fuzzy Decision Making in Fuzzy Environments', is proposed. Fuzzy models are based on the reasoning and perception of the human being and allow change of domain to the variables or functions studied. Within the 'Decision Making Theory', the uncertainty associated with the desired result obtained is called as 'Fundamental Uncertainty'. In this way there are degrees of acceptance of a certain variable to a given set. This mean, the certainty or risk of accepting a given alternative is possible to be modeled using fuzzy sets [3-6]. Based on this, an index called Intrinsic Cost Index is proposed, which models the penalty cost for non-compliance with quality standards.
Regarding the solution method, the metaheuristics qualities are exploited as flexible methods of problem solving. In this aspect, the Particle Swarm Optimization with Constriction Factor (CF PSO) metaheuristic was applied [7].
Then, these three aspects define the methodology named as CF PSO with extension to the Fuzzy multiobjective domain or CF FPSO [8].
The objective of this methodology is to propose a regulation model of the MVPDS, to establish the penalties for breach of quality of supply.
2.2. Model scope
The optimization model was applied to a case of MVPDS taken from real data and studied in the state of the art using Mono and Multi-criteria models.
The objective is to determine the optimal location of SP devices of different types, optimizing four criteria: Investment Cost USD year s, ENS kWh year , SAIFI 1 year and SAIDI hs year .
The main characteristics of the operation of each device are:
Fuses (F) operate only in the event of an active fault, disconnecting the entire network segment downstream and leaving it unplugged. They do not allow maneuvers and must be replaced in the event of any failure of their drive.
Disconnectors (D) do not operate automatically in the event of an active fault. Their function is to disconnect the entire network segment downstream to enable safe maneuvering, taking into account that they are not designed to be operated when they are under load.
Interrupters (I) operate when an active fault occurs and allow the network segment downstream to be disconnected or connected under load. Associated with the reconnection, a waiting time is required for the cooling of the oil that extinguishes the arc generated during the cutting process before being able to reconnect it. They can be remote controlled.
The considerer planning horizon is a single year. Also, all the SP devices are supposed correctly installed, so, there are no failures because of installation defects.
Among the hypotheses and simplifying assumptions of the problem, a network that complies with the restrictions of radiality is considered; both the ideal SP devices and the ideal Distribution Transformer Station (DTS) do not have failure rates associated with their operation. The device which operates in case of a fault is the one closest to the fault upstream.
The operating restrictions of the network are supposed satisfied, regardless of the selected alternative: there are no operational limits for SP and substation transformer distribution. No distinction was made between the fault types and the problem was simplified taking into account three phase faults (the three of them failing simultaneously).
The parameters are considered fixed, and independent of the state of operation of the network.
No distinction or logistic analysis that takes the reparation team from one point of the network to another is made.
It is assumed that there are action plans (repairs and maneuvers) that comply with the corresponding safety standards, in order to ensure the integrity of personnel and devices in case of electric risk.
2.3. Model parameters
In addition, the network data on which the model is defined are required. These are the lengths of stretches [km], the power required [kVA] and the number of users.
2.4. Definition of decision variables and resulting search space
Xj: represents the decision to place (or not) an SP devices on the j-th section of the network. The 3 types of devices are coded: Fuse (F), Disconnector (D), Interrupter (I). This definition of variables considers that in each section only one SP of the 3 types (or no devices) can be placed. That is why the quantity of solutions for this problem is given by the permutations with repetition of 4 elements, taken from to nT, where nT is the number of sections of the network.
This search space therefore has 4 nT solutions.
2.5. Definition of objective functions
Energy Not Supplied (ENS) due to service interruption:
Where P k is the demanded power of node k, and t k is the time that the node is interrupted in the period considered.
System Average Interruption Frequency Index (SAIFI):
Where N i is the number of clients affected by the i cut, and N T is the total number of clients.
System Average Interruption Duration Index (SAIDI):
Where T i is the time duration of the cut i.
Devices Acquisition and Maintenance Cost:
In the case of Interrupters and disconnectors, it is the investment cost affected by the capital recovery factor.
Where E P is the price of the SP devices and CRF is calculated as:
In the case of fuses, the cost associated with each one is that of acquiring and locating it, plus replacing it for each fault affecting it.
2.6. Fuzzy multi-objective optimization model
2.6.1. Mathematical model
The location of Devices of different types in the network determines different effects on the loads connected to it. This is according to which device is closer (upstream) to these loads. The interrupter devices segment the network and have two functionalities: reaction to failures and maneuver under load. Within a segment, that is, in the part of the network between two Interrupters, there can be many combinations of lines, loads (users), fuses and disconnectors.
The different combinations determine which of the users are left without supply and for how long (see Table 1).
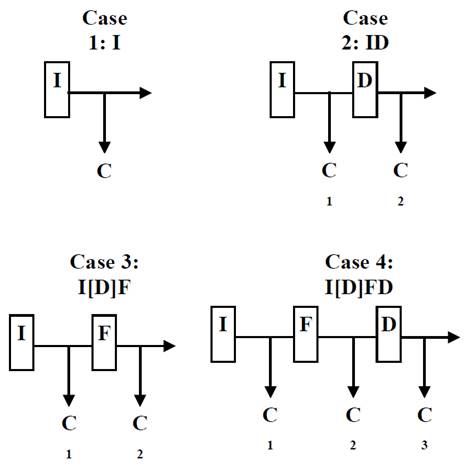
The following four cases summarize all the configuration possibilities of a segment for these three types of device, illustrated in Fig. 1. All other combinations are redundant with respect to these four types.
Case 1: Interrupter (I)
In this case, which is the most basic, there is only a combination of lines and loads between two Interrupters. If there is a failure in any of the sections, the entire network downstream of the switch is left without supply and cannot be restored to any of them until the fault is repaired. It is assumed that in the root node of the network there is an interrupter properly located.
Case 2: Interrupter Disconnector (ID)
In this case, before a fault in a section between I and D, proceed as in case 1. For a fault after D, I is actuated and left without supply downstream. However, the supply for the sections between I and D can be restored by opening D, thereby disconnecting the entire network downstream from D and by actuating I to restore the service to users between I and D. Once a fail occurs, D must be actuated to restore the downstream service, but first I must be pressed to interrupt the supply again. Once the cooling time of Iis over, the service is restored throughout the network.
Case 3: Interrupter Disconnector Fuse (I D F)
In this case, for a fault in a section between I and F, proceed as in case 2 or 1, depending on whether D is located. For a fault after F, this is triggered and left without supply downstream. Users between I and F are not affected by the cut.
Note that there may be devices of typeD between I and F which are of no use in this case. Once the fault has been repaired, F must be replaced, for which the supply downstream of I must be interrupted. Assuming that the cooling time of I is greater than the fuse replacement time, and after t CD is over, the network service is restored.
Case 4: Interrupter Disconnector Fuse Disconnector (I D FD).
In this case, when a fault occurs before D, proceed as in the previous case. For a fault after D, F is operated leaving no downstream supply. The fault does not affect the upstream of F. However, considering t r > t CD , the supply to users can be restored between F and D, opening D and replacing the corresponding fuse.
For the latter, it is necessary to cut off the supply from I, replace F and wait for the cooling time to re-start I, taking into account that D must be opened before completing the process. Once this first maneuver is performed, the fault is repaired and I must be restarted, cutting the supply, pressing D and waiting t CD to restore the supply downstream of D.
2.6.2. PSO Metaheuristic
The use of Metaheuristics makes it possible to obtain algorithms of general purpose, offering solutions which are generally satisfactory for a vast number of problems. This method is easy to implement and can be used with parallel processing. Within the set of metaheuristics available in the state of the art, the PSO metaheuristic is used due to its wide versatility, ease of implementation and good performance. The set of variants of the PSO metaheuristic is known as X-PSO forms.
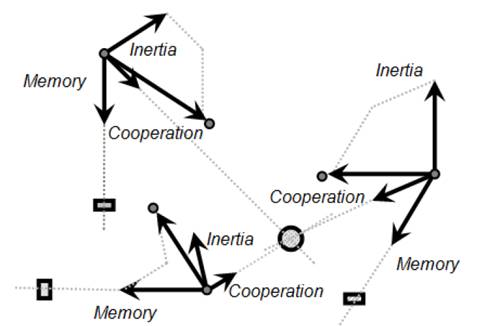
In the Classic PSO model there is a set of alternatives called population or swarm (whose feasibility exhibits degrees of aptitude), which are called particles. From one iteration to the next, each particle moves in the search space, according to a certain rule of motion that depends on three factors, which are explained below. Vector b i k represents the best positions that the particles have reached individually in the previous iterations (an aspect referred to in the model as past life of the particle); Then it will correspond to the individual optimum of the particle i in its past life. In the same way, the global optimum achieved by the particle system will be indicated by b G k until the present iteration, according to the rule of motion in eq. (6) [7]:
The velocity vector for the i-th particle is expressed in eq. (7):
This rule of movement was represented in Fig. 2.
The term V i k represents the inertia or habit of the particle i: tends to maintain its motion in the direction in which it moved in the previous iteration.
The term w C ∙ r 1 k ∙ b i k − X i k represents the memory or cognitive ability of the particle: it is attracted to the best point in the search space achieved individually in its past life.
And the third term w S ∙ r 2 k ∙ b G k − X i k represents the cooperation between the whole swarm, or social capacity of the particle with respect to the swarm: the particles share information on the best overall position reached by the swarm.
The incidence of these factors on each particle is given by the constants or parameters of the model, w c and w s . The parameter w c is called cognitive constant and the parameter w s is called the social constant of the swarm.
The random numbers r 1 k and r 2 k are uniformly distributed in [0,1], U[0,1], and their objective is to emulate the stochastic behavior exhibited by the population or swarm in each iteration (somewhat unpredictable).
2.6.3. Particle swarm optimization metaheuristic with constriction factor
With this modification of the Classic PSO model a better convergence of the particles in time is promoted, by the constriction or reduction of the particle oscillation amplitude as they are focused on a certain focal point. In this case, the classical speed operator is modified as follows:
Where χ is called the Constriction Factor, and is obtained by the following expression:
A commonly used parameter configuration is φ=4.1, φ M = φ C =2.05. This results in a value of χ≈0.73.
When κ=1, the convergence is slow enough to allow detailed exploration before the search stabilizes at the point of maximum fitness found [7].
2.6.4. Extension to Multiobjective Domain according to decision theory in Fuzzy environment
Bellman Zadeh's principle:
Although the approach originally adopted by the PSO metaheuristic was Mono-Objective, in reference [7] an extension to the Multi-Objective domain of the EPSO is proposed. This method is referred to as FPSO (Fuzzy PSO), for the use of Fuzzy Sets. As detailed in the above mentioned reference, they are able to capture non-stochastic value uncertainties.
To formalize the multiobjective extension, the application of the principle of decision making in fuzzy environments formulated by Bellman and Zadeh is proposed [3-6]. This extension, applicable to any variant strategy of the classical PSO metaheuristic, is the one used in this work.
Consider a set of fuzzy objectives {O}={ O 1 , O 2 ,…, O n } whose membership functions are μ Oj , with j=1..n, and a set of fuzzy constraints {R}={ R 1 , R 2 ,…, R h } whose membership functions are μ Ri with i=1..h.
The Decision fuzzy set, results:
Where C is a fuzzy sets operator called “confluence”.
The most common confluence, is the intersection.
Then, the membership function of D is expressed as:
Where C is an operator (called, in general, t-norm) between values of membership functions.
For example, if the confluence for certain instance is C ≡∩ (intersection), then C is the t−norm≡min (minimum value of all membership function in eq. (11)).
If t x,y : 0,1 × 0,1 → 0,1 is a t-norm, then: a) t 0,0 =0;t x,1 =x; b) t x,y =t y,x ; c) if x≤α and y≤βt x,y ≤t α,β ; and d) t t x,y ,z =t x,t y,z . Notice that all fuzzy sets (Objectives and Constraints) are “mapping” in the same fuzzy set of decision, D, and are treated the same way.
The crisp set S of “optimal” solutions or alternatives x ∗ is:
Fuzzy membership functions used:
For each objective (or restriction), the fuzzy functions associated to their objective or restriction are defined as follows: consider an upper and a lower limit in the possible values of the variable corresponding to a certain objective or constraint m, v m . These limits are referred to as v m Sup y v m Inf , respectively.
When v m ≤ v m Inf the fuzzy function μ m = 1, since v m is required to be minimized. Farther, when v m ≤ v m Sup , μ m =0 for the same reason. The fuzzy bounds of v m in [ v m Inf , v m Sup ] are calculated by the equation of the line passing through the points ( v m Inf , 1) and ( v m Sup , 0). In this way, the degree of satisfaction of the objective decays as it moves away from the value v m Inf and is not accepted from the value v m Sup .
In addition, let EW m be its exponential weight, whose effect on the fuzzy function is its contraction ( EW m >1) or dilation ( EW m <1). In this way, there is greater or minor importance of the criteria analyzed in the total fitness function. For the case EW m =1, the assumed membership function is linear. The lower and upper bounds of the fuzzy functions were obtained by simulations for the extreme scenarios. The upper boundaries correspond to the network without inversion in devices (except investment cost). The lower boundaries correspond to the network with Interrupters in all the sections.
The aptitude function μ D was obtained with the t-norm called Einstein Product, whose arguments are the membership functions of fuzzy functions associated to each objective. All the values used are shown in the results section.
The fuzzy functions of CE and ENS were presented in eq. (13) and (14).
Definition of the t-norm used:
The confluence operator must be established between the fuzzy sets in order to obtain the maximizing decision that will define the value of the fuzzy fitness function at each iteration of the F-PSO. For this, a t-norm is used, which is a function t defined in the interval [0, 1]([0, 1] also applied in [0, 1]. In the state of the art the Einstein Product was adopted:
Where x and y are generic membership functions. Then the fuzzy maximizing fitness function for the reliability problem is:
Intrinsic Cost (IC):
In the present research line, the economic valuation of the optimized criteria was made through the 'Intrinsic Cost' index (IC). This was defined by the derivative of the variable related to the criterion to be optimized, with respect to the variable generally related to the cost:
Where ∂ μ CE ∂CE and ∂ μ ENS ∂ENS are the derivative of the criteria analyzed with respect to their fuzzy functions (see eq. (13) and (14)).
Then the expression of the IC is:
In these works, the mathematical expression to determinate ∂μ CE ∂ μ ENS was obtained from the aptitude function applying the clause 'Ceteris Paribus'. This clause, which is generally used in economy, stands for 'all other things being unchanged or constant'. Then, the other variables associated with the optimization criteria were considered constant. From this assumption, by expressing the membership functions of these criteria and the t-norm used, the cost criterion was expressed as a function of the variable associated with the desired variable. This approach leads to extensive mathematical expressions when the number of objectives to be maximized or minimized is large. Therefore, another expression of intrinsic cost is proposed, by changing the development of one of its components. It starts from the membership function obtained from the fuzzy relationship between the investment cost criterion and ENS criterion as follows:
The logarithmic function and the properties associated to the product and division was applied to the eq. (21).
Differentiating the eq. (22) with respect to the fuzzy function μ CE .
Where f μ ENS , μ CE is the derivative of the third term of eq. (22).
Given that ∂ logμ ∂ μ CE =0, then the following is obtained:
Economic Penalty:
From the intrinsic cost of the ENS, the economic penalty is defined (see eq. (20)), and this refers to the resulting cost because the optimal alternative has not been selected.
Where EN S ∗ refers to the optimal (most satisfactory) Energy Not supplied and ENS′ refers to the non-optimal alternative. IC ENS ∗ , is obtained from (17).
Multi-objective analysis for each node of the studied system:
An analysis of each node of the MVPDS was proposed through the application of the fuzzy multiobjective extension for the analyzed criteria: ENS and CE. Following this proposal, the eq. (20) can be expressed for each node in the system, obtaining the intrinsic cost and the economic penalty per node. This progress makes it possible to distinguish penalties according to the importance and impact of each node.
The ENS at each node was obtained through an extensive and deep analysis of the impact that each load has on the total Energy Not Supplied. Due to the depth and complexity of this analysis, the algorithm and computational model required has not been described in detail in this work. Device Acquisition Costs for each node were obtained simply by observing the type and cost of the device installed.
3. Results and discussion
3.1. Electric power distribution system studied
The system considered represents the Electric Power Distribution System (MVPDS) of Concepción del Uruguay, Argentina, and the information used in this work was estimated by means of surveys done to similar MVPDS.
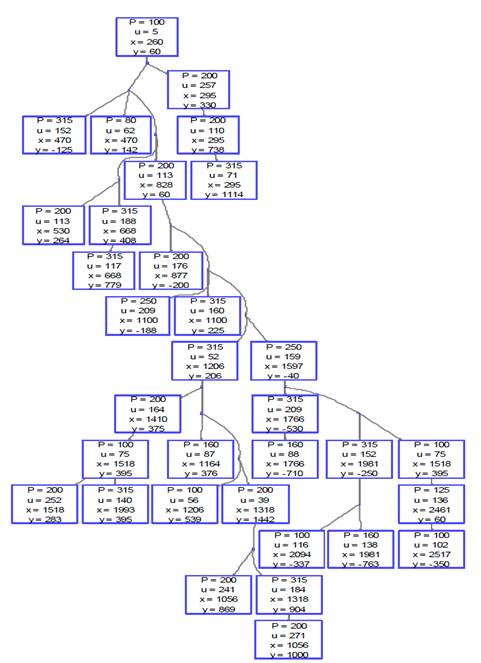
The system considered corresponds to the output of a Transformer Station (TS) 132 / 13.2 kV and it has 35 loads and 47 sections.
In Fig. 3, the technical characteristics of the distribution system analyzed are presented. The parameter 'P' is the installed power of the TS, 'u' is the number of connected users, 'x' and 'y' are the respective TS coordinates.
The values used for all the parameters were: λ j =0.32, C I =12000, CD = 4000, CF = 50, ULI = 15, ULD=5, t d =0.12, T c =0, T p =0, T l =0.5, T r =2.5, T CD =0.5. Where j is the section of the network.
3.2. Analysis of the obtained results
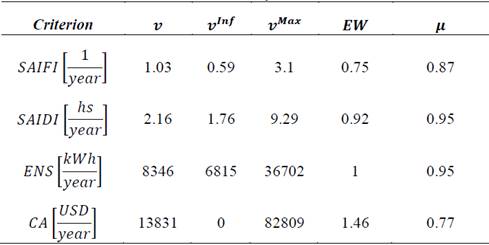
The criterion values and the results of the fuzzy functions are shown in Table 2, where v, v Inf , v Sup , EW i , μ refer to obtained value, lower limit, upper limit, exponential weight and degree of membership, respectively.
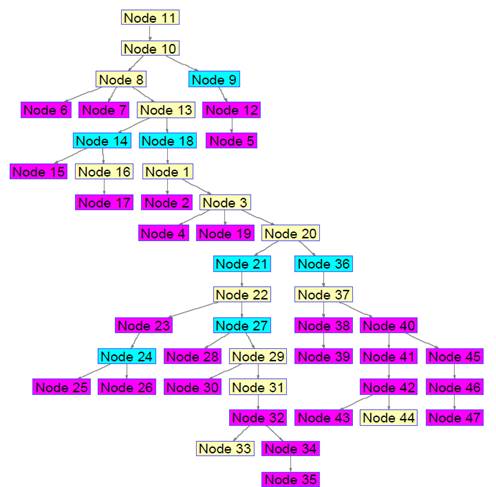
The solution found by CF FPSO shown in Fig. 4. helps to locate the interrupters in the magenta nodes, and fuses are located in the cyan nodes. A 64-particle CF FPSO swarm was used in the resolution, finding the solution described in approximately 800ms. This is explained by the fact that the search space is relatively small ( 4 47 =1.98∙ 10 28 ). The solution obtained helps to find a strategy to locate fuses in the nodes {2 4 5 6 7 12 15 17 19 23 25 26 28 30 32 34 35 38 39 40 41 42 43 45 46 47}, and interrupters are located in the nodes {9 14 18 21 24 27 36}. No disconnectors are used.
Source: The authors.
Figure 4 Optimal SP location obtained using the metaheuristic Fuzzy Particle Swarm Optimization with Constriction Factor (CF FPSO).
The final fitness obtained by Einstein's Product was u EP =0.55. The values of each criterion and the configuration of the associated fuzzy sets are shown in Table 2, where U m , U min , U max , EW m , u m refer to obtained value, lower limit, upper limit, exponential weight and degree of membership, respectively.
Annualized investment in protection devices resulted in 13831 USD year , which is well below to place interrupters at all nodes (82809 USD year ).
The Energy Not Supplied was 8346 MWh year (1.8 of the total demanded energy), very close to the minimum scenario (1.4≤ENS≤7.8). Therefore the results obtained by the proposed method are satisfactory.
Annualized investment in protection devices resulted in 13831 USD year , which is well below to place interrupters at all nodes (82809 USD year ).
The Energy Not Supplied was 8346 MWh year (1.8 % of the total demanded energy), very close to the minimum scenario (1.4≤ENS≤7.8).
If the penalty is done according to the results in Table 2, a result of 38112 USD per year is obtained. If the total investment is 85300 USD, the difference when the penalty is not paid is that the investment can be recovered in about two years.
3.3. Map of the energy not supplied, intrinsic cost and economic penalty
The term map refers in this paper to the use of two-dimensional figures where the values of the indices studied in a scale of colors. The coordinate axes '𝑥' and '𝑦' are the distance with respect to a point of reference, towards the east and towards the north respectively. This color scale is associated with a three-dimensional curve (z-axis), which represents the variable studied. The origin of coordinates 0,0 represents the main feeder node of the distribution system studied. Performing interpolation calculations between nodes were used to improve their visualization and understanding.
A map for the most satisfactory solution is presented in Fig. 5 to 7.
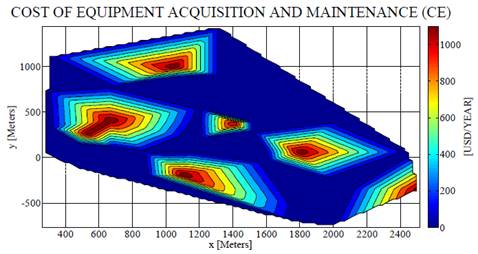
The Fig. 5 shows the areas where the greatest investment was made in equipment. The costs associated with the installed Device (F, D or I) are represented in the color bar. The red color indicates the extreme case that a Device SP was installed in the node, while the blue color indicates the extreme case in which no device was installed.
Source: The authors.
Figure 5 Map of the cost of Device acquisition and maintenance of the studied system.
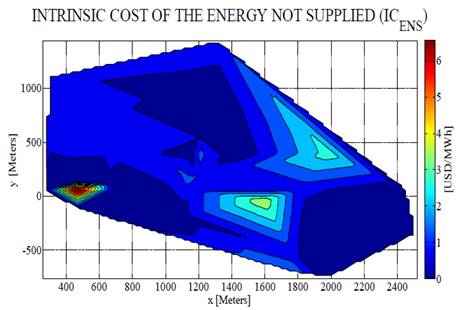
The Fig. 6 shows the map of Energy Not Supplied for the worst alternative (no SP device installed). In this case, the most expensive nodes are those that have transformation centers of higher demanded power, which corresponds to the red color.
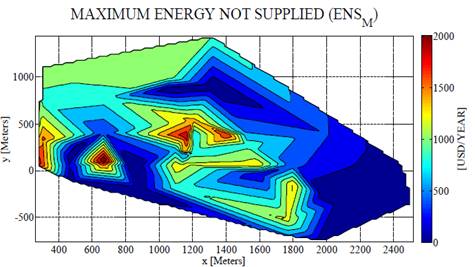
Source: The authors.
Figure 6 Map of the Energy Not Supplied Maximum ( 𝐸𝑁𝑆 𝑀 ) of the studied system.
The Fig. 7 shows the map of Energy Not Supplied for the most satisfactory alternative.
The installation of the interrupters considerably lowered the ENS in the high demand nodes. Moreover, there were peaks of ENS in those nodes without investment, as shown in Fig. 6 and 7. The Fig. 6 shows the Intrinsic Cost Index of the Energy Not Supplied (ENS), where it is also observed that those nodes where no investments were made have a higher cost than the others. Therefore, the analysis of the maps for the CE and ENS criteria shows that the most satisfactory solution obtained by the fuzzy multiobjective model responds satisfactorily (see Fig. 6 and 7).
The expression obtained for the intrinsic cost index is congruent with these analyzes and the values are in accordance with the penalties applied to the provincial regulators of Argentina.
4. Conclusions
The conclusions of this article are presented in this section. There are different aspects to take into account: the problem to solve, the mathematical model proposed for it and the solution method.
1) The problem corresponds to the reliability of the distribution systems, where in the state of the art multiple modeling and resolution mechanisms were applied. The present paper applied a novel modeling method based on the 'what if' clause. In this way the effect of each device used is obtained (Disconnector, fuse and Interrupter).
2) As a result of this approach, the effect of the placement of each SP device on each studied node could be analyzed, grouping it only in 4 cases. The modeling by this means did not require complex studies and allowed to obtain reliability indices according to the regulations in force.
3) Concerning the resolution method, a fuzzy multi-objective model based on the works of Bellman and Zadeh, the theory of fuzzy decision, was proposed. Comparatively with the previous version of this problem, the use of different SP devices prevents the use of dynamic programming to solve this problem. Then, to obtain the optimal alternative that maximizes the fuzzy fitness function, the metaheuristic Fuzzy PSO with Constriction Factor was applied. This metaheuristic is relatively simple to implement and produced very good results in less than a second. It would not be possible to easily solve this problem with mathematical programming techniques.
4) A contribution was made in the state of the art of the theory of fuzzy decision making and other areas, the Intrinsic Cost (IC) index. This index allowed us to obtain cost indicators associated with Energy not supplied reliability index through its preference value. In this way, maps were obtained with this index, which allow to study the efficiency of the network in a geographical way and to know which nodes of the electrical network are inefficient or vulnerable.
5) The results obtained were in accordance with the current regulations of the Argentine distribution electricity market.
5. Acronyms
DTS: Distribution Transformer Station.
MVPDS: Medium Voltage Power Distribution Systems.
ENS: Energy Not Supplied.
IC: Intrinsic Cost.
SAIDI: System Average Interruption Duration Index.
SAIFI: System Average Interruption Frequency Index.
SP: Sectioning/Protection.
I: Interrupters.
F: Fuses.
D: Disconnectors.
PSO: Particle Swarm Optimization.
FPSO: Fuzzy Particle Swarm Optimization.
FC PSO: Particle Swarm Optimization with Constriction Factor.
CF FPSO: Fuzzy Particle Swarm Optimization with Constriction Factor.