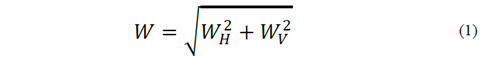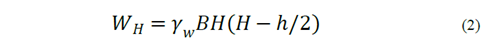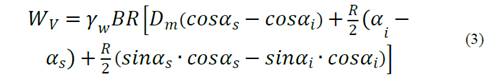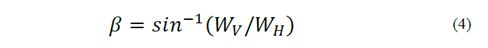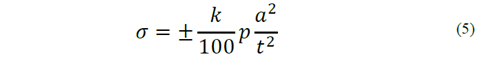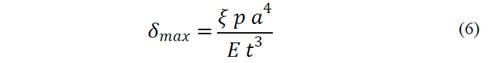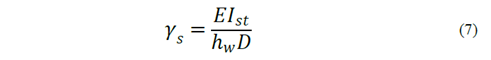1. Introduction
Curved plate elements have traditionally been used in mechanical, aeronautical and marine/off-shore engineering. These structural elements are found in the fuselage of aircrafts, oil and gas storage structures, cooling towers and ship hulls. Their applications in civil engineering are relatively recent and mainly focus on the construction of steel bridges. Typical examples of curved panels in bridge engineering are orthotropic decks in box-girder bridges and webs of in-plane curved I-girders.
Stiffened curved plates are also becoming more and more popular as recent developments of the curving process allow for a faster and more economic manufacturing. Nevertheless, their design is complex and difficult due to the lack of standard building code specifications [1], few studies related to their stability are available in the literature [2-4]. Consequently, curved plate analysis and design rely significantly on expensive and time-consuming finite element modeling [2,3].
Recently, the influence of longitudinal stiffening on both, critical and ultimate strength of plate girders has been investigated [5-7]. The primary function of the stiffeners is to control out-of-plane displacements of the thin-walled webs and increase bending resistance.
This paper presents a numerical investigation on the elastic behavior of stiffened curved plates subjected to transversal loading. A parametric study is performed through finite element analysis to evaluate the beneficial effects of including longitudinal and transverse stiffeners on the performance of curved plates. Firstly, the numerical model is validated against theoretical formulae available in the literature. Then, a case study is further analyzed to evaluate the response of a hydroelectric power plant intake radial gate subjected to a hydrostatic head. At the end, the results show that stiffeners are a practical way to retrofit existing structural elements as they increase the system stiffness and reduce transversal deformations, which is directly reflected in an improvement of system reliability.
2. Numerical modeling
This section presents a numerical study conducted to investigate the influence of transversal and longitudinal stiffening on the out-of-plane displacements of stiffened curved plates subjected to transverse loading.
Various computational models for plates under transversal loading are elaborated using the finite element software ANSYS [8]. A detailed description of the employed numerical models can be found in [9]. These models are validated using a procedure that considers the influence of the plate geometry (flat and curved), boundary and loading conditions and finally considering the presence of transverse and longitudinal stiffening. Thereafter, a more complex numerical model is elaborated to investigate the influence of the stiffening on the out-of-plane displacements and stress distribution of a curved plate.
The material used in all analyses is an ASTM A516 Gr 70 steel, with Young’s modulus, E= 206 GPa; Poisson ratio, 𝜐= 0.3; density, 𝛾= 7.85×10-6 kg/m3; yield strength, 𝑓 𝑦 = 260 MPa and ultimate strength 𝑓 𝑢 = 485 MPa.
2.1. Flat plates under transverse loading
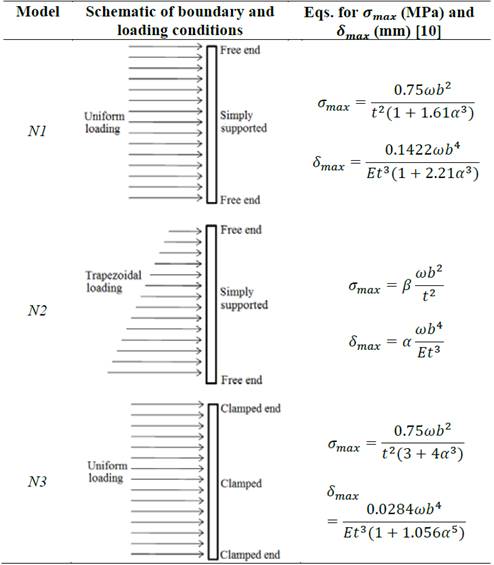
As mentioned above, the first step into the validation procedure of the numerical methodology is to investigate the influence of boundary and loading conditions on the structural response of flat plates subjected to transverse loading. In this regard, Table 1 shows a schematic view of boundary and loading conditions for the three numerical models developed for flat plates herein: Model N1 with the upper and lower ends free to move and the lateral ends simply supported, under uniform transverse loading (𝑝 = 0.001 MPa); Model N2 with the upper and lower ends free to move and the lateral ends simply supported, under non-uniform (trapezoidal) transverse loading (𝑝 = 0.01667 MPa); and Model N3 clamped at four ends, under uniform transverse loading (𝑝 = 0.001 MPa).
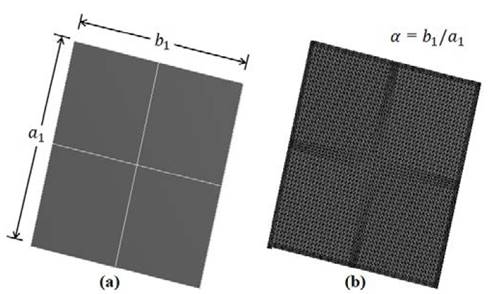
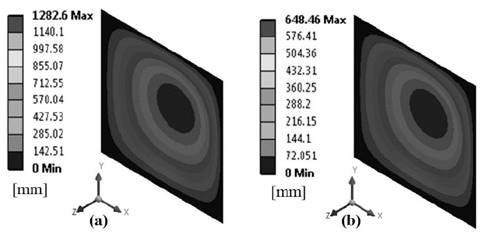
Table 1 also shows formulas for the calculation of maximum stresses 𝜎 𝑚𝑎𝑥 and displacements 𝛿 𝑚𝑎𝑥 [10]. Shell181 elements from the ANSYS element library [8] were used to model the plates. The dimensions of the plates were: width, 𝑏 1 = 10000 mm; height, 𝑎 1 = 10000 mm; and thickness, 𝑡 𝑝 = 20 mm (see Fig. 1a). An additional parametric study was conducted regarding the panel aspect ratio, 𝛼= 𝑏 1 / 𝑎 1 = 1.5, 2 and 2.5, maintaining constant the height, 𝑎 1 = 10000 mm. Fig. 1b shows a representative mesh of the flat plates, while Figs. 2a and 2b show the out-of-plane displacements plots obtained numerically for Models N1 and N2, respectively.
Source: The authors.
Figure 1 (a) Dimensions for Models N1, N2 and N3, and (b) Mesh for flat plates.
Source: The authors.
Figure 2 Radial displacement with 𝑝 = 0.001 MPa and 𝛼=1: (a) Model N1 and (b) Model N2.
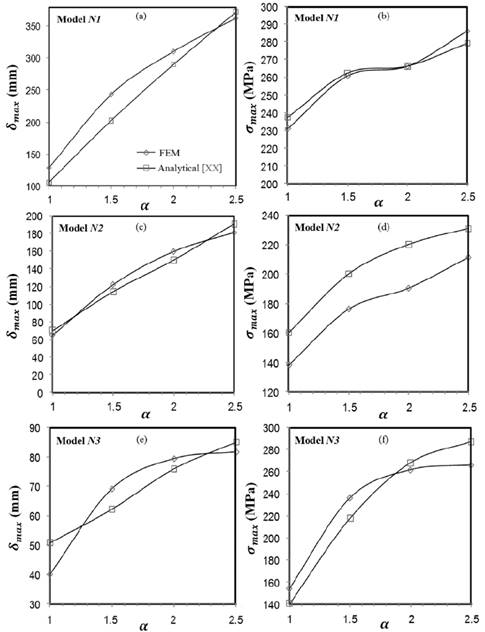
Fig. 3 shows a comparison for maximum displacements and stresses, between computed values and those obtained analytically with the equations proposed by [10] and summarized in Table 1. A good agreement between numerical and analytical results is achieved with a maximum difference of approximately 10%. It is worth noticing that the available formulas were obtained for stresses and displacements in the elastic range. Even though, the stresses are slightly higher than the corresponding yield strength of the material ( 𝑓 𝑦 = 260 MPa). The figure shows that for Model N1 the maximum radial displacement increases with the panel aspect ratio, 𝛼. For Model N2, with the same boundary conditions as Model N1 but different load distribution, the maximum radial displacement reduces about 30% compared to Model N1. For Model N3, clamped in all ends and uniformly loaded, the maximum displacement is reduced around 50% with regards to Model N1. These results demonstrate the impact of boundary and loading conditions on both, maximum displacements and maximum stress when modeling flat plates subjected to transverse loading. The results also show that both, the maximum displacement and the maximum stress increases with the panel aspect ratio for the three Models (N1, N2 and N3).
2.2. Curved plates under transverse loading
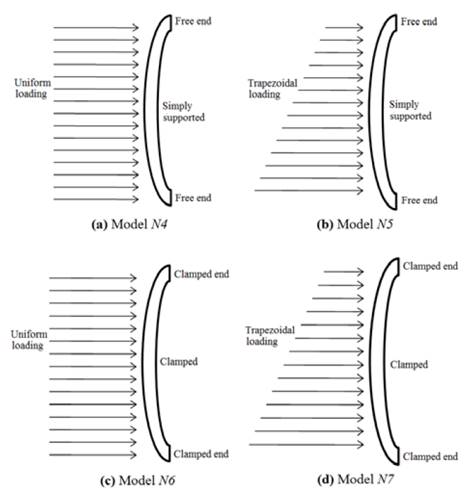
Continuing the methodology applied for flat plates, this section aims at investigating the influence of boundary and loading conditions on the structural response of curved plates subjected to transverse loading. Four additional models were developed as shown in Fig. 4, hence: Model N4 with the upper and lower ends free to move and the lateral ends simply supported, under uniform transverse loading (𝑝= 0.1 MPa); Model N5 with the upper and lower ends free to move and the lateral ends simply supported, under non-uniform (trapezoidal) transverse loading (𝑝 = 0.1 MPa); Model N6 clamped at four ends, under uniform transverse loading (𝑝= 0.1 MPa); and Model N7 clamped at four ends, under non-uniform (trapezoidal) transverse loading (𝑝 = 0.1 MPa).
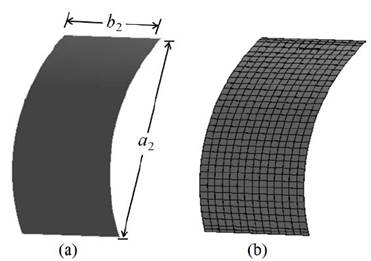
Fig. 4 shows a schematic view of boundary and loading conditions of the four models. Shell 181 elements from the ANSYS element library [8] were also used to model the plates. The dimensions of the plates were: width, 𝑏 2 = 10000 mm; height, 𝑎 2 = 10000 mm; plate radius, 𝑟= 9500 mm; and thickness, 𝑡 𝑝 = 10 mm. The panel aspect ratio, 𝛼= 𝑏 2 / 𝑎 2 (see Fig. 5a), was varied as 𝛼= 1, 1.5, 2 and 2.5 maintaining constant the height, 𝑎 2 = 10000 mm. Fig. 5b shows a representative mesh of the modeled curved plates.
Source: The authors.
Figure 5 (a) Dimensions for Models N4, N5, N6 and N7; and (b) Meshing for the curved plates.
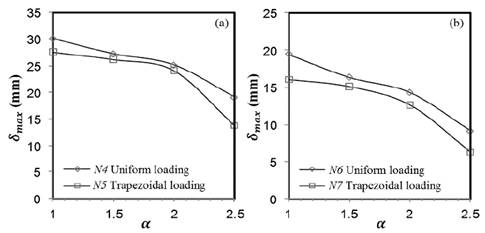
Regarding the influence of the loading conditions, Fig. 6 shows a comparison between numerical results of the out-of-plane displacements for Models N4, N5, N6 and N7. In these cases, the radial displacement decreases when the panel aspect ratio increases, for both conditions, simply supported (Fig. 6a) and fully clamped (Fig. 6b). The reduction in the magnitude of the displacement between the former and the latter is close to 30%. When comparing the displacements for the two loading types with same boundary conditions the obtained difference is abou10%.
2.3. Stiffened curved plates under transverse loading
In this section, a third parametric study is conducted to investigate the influence of transversal and longitudinal stiffening on the maximum out-of-plane displacement of curved plates. At this stage, it is important to quote that simply supported and trapezoidal loadings are the corresponding boundary and loading conditions for curved plates. Hence, the current analysis is performed taking into account these conditions. Hot-rolled profiles are currently used in the steel industry to stiffen plated structures.
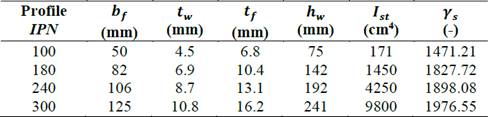
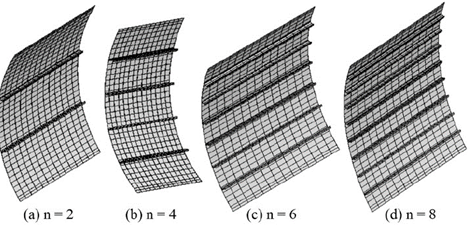
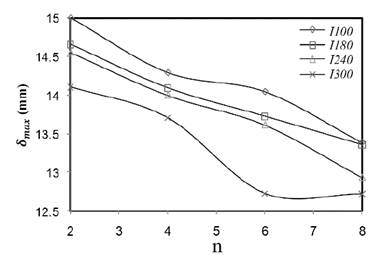
The geometry parameters of four (4) IPN steel profiles, namely IPN100, IPN180, IPN240 and IPN300 used in this study, are listed in Table 2. Fig. 7 shows the corresponding numerical models for different number of transversal stiffeners and Fig. 8 presents the results for the maximum radial displacements in the plane of symmetry of the curved plate considering the different profiles. As expected, the stiffener with the largest second moment of area (IPN300) gives the largest reduction in out-of-plane displacements of the curved plate.
Source: The authors.
Figure 7 Models considering transversal stiffening (n = 2, 4, 6 and 8 stiffeners).
Source: The authors.
Figure 8 Maximum radial displacement 𝛿 𝑚𝑎𝑥 in the plane of symmetry of the curved plate (n = 2, 4, 6 y 8 transversal stiffeners).
To complete the study regarding the effect of stiffening on the deflection of curved plates, it is necessary to investigate the combined case with transversal and longitudinal stiffening.
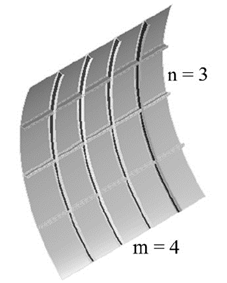
In this analysis, only one stiffener IPN100 was considered in the study. The number of the stiffeners in both directions was varied in both, the transverse direction (n= 3, 4, 6 and 8) and longitudinal direction (m= 4, 6 and 8). Fig. 9 shows a model with seven stiffeners, four in the longitudinal and three in the transversal direction. Boundary and loading conditions are the same as in the previous case.
Source: The authors.
Figure 9 Model considering combined stiffening (longitudinal m = 4 and transversal n = 3).
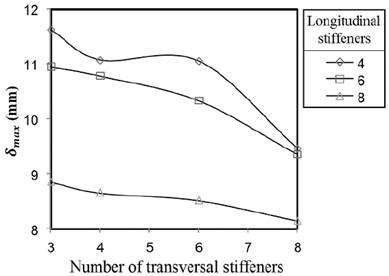
Fig. 10 shows the results for the maximum radial displacement achieved with the stiffener’s combinations investigated. It is observed that the radial displacements are reduced significantly for 8 longitudinal stiffeners. A reduction of 20% in the radial displacement is observed in Fig. 10, when compared to the corresponding displacements for only transversal stiffeners. Obviously, a larger displacement reduction may be achieved by using larger stiffeners.
3. Applications
Intake gates are among the main elements regarding dam safety in a hydroelectric power plant as they control water levels in the reservoir. When the water level rises, the pressure on the gates increases and excessive deformations can take place compromising the safety of the reservoir [11-13]. In many cases, intake gate systems have surpassed the service life for which they were designed for the original operating conditions, such as hydrostatic load, opening and closing frequency, among others, have been significantly modified to meet new energy generation requirements. All this is reflected on structural changes of intake gates and their possible failure, which can yield the electric plant unserviceable and in some cases the collapse of the reservoir. That is precisely why intake gate systems require rehabilitation works to improve their operation and adapt to current operating requirements.
In this section, the performance of the intake radial gates of the Antonio José de Sucre - Macagua I Hydroelectric Power Plant [14] is investigated. For this particular case, the intake radial gates were originally designed to withstand a hydrostatic head at an elevation of 48.0 m.s.n.m. In recent years, the water level of the reservoir was raised to 54.5 m.s.n.m. to accommodate for the increase in energy demand [15]. This increase in the level of the reservoir resulted in large gate deformations causing excessive water loss.
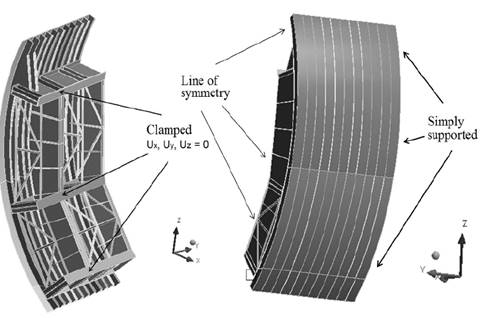
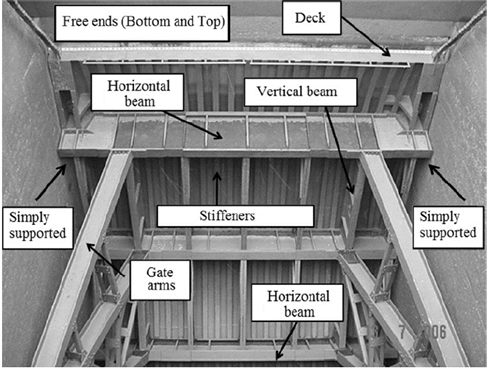
Fig. 11 shows a picture of the radial gate of the Antonio José de Sucre - Macagua I Hydroelectric Power Plant and its main structural components. Table 3 lists the geometry and dimensions of the radial gate. Due to symmetry in load and boundary conditions only one-half of the gate is modeled as shown in Fig. 12. The longitudinal and vertical stiffeners were modeled using BEAM44 elements from the ANSYS element library [8]. Accordingly, the plate in the gate was modeled using SHELL 181 elements, the remaining parts were modeled with SOLID 187 elements. Also included in the figure are the boundary conditions used in the numerical model for the radial gate. In the middle, a symmetry line was established, the other ends of the gate were simply supported. In the horizontal beam, clamped conditions were used to consider the support provided by three stiff arms that maintain the gate in place.
Source: [9].
Figure 11 Radial gate of the Antonio José de Sucre - Macagua I Hydroelectric Power Plant.
After conducting a convergence analysis, a mesh with 142.593 elements was chosen. Fig. 13 shows the meshing used in the main supporting elements and the radial panel.
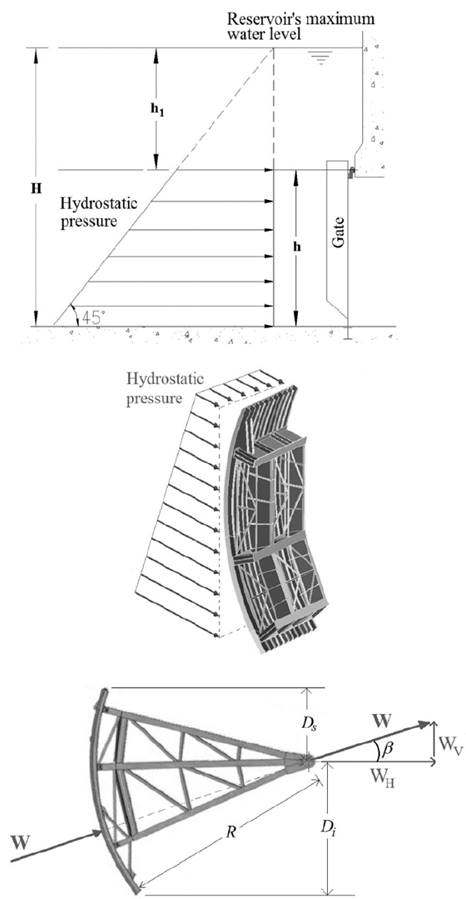
In practice, radial gates sustain high transversal loadings due to the hydrostatic pressure gradient. Its determination is precisely the first step to adequately size a radial gate [16]. An upper bound for the hydrostatic pressure gradient acting on the gate can be defined using the maximum expected water level of the reservoir as shown in Fig. 14.
The magnitude of the resultant hydrostatic load, 𝑊, can be found as:
where 𝛼 𝑠 = 𝑠i𝑛 −1 ( 𝐷 𝑠 /𝑅), 𝛼 𝑖 = 𝑠𝑖𝑛 −1 ( 𝐷 𝑖 /𝑅), 𝐻 is the maximum expected water level of the reservoir, ℎ 1 is the depth to the radial gate, ℎ is the height of the gate, 𝐵 is the width of the gate, 𝑅 is the radius of the gate, 𝛾 𝑤 is the specific weight of water and 𝐷 𝑚 is depth to the point of curvature of the gate. The line of action of the resultant hydrostatic load on radial gates is assumed to pass through the point of curvature of the gate [16] at an orientation:
Based on the above loading conditions, two design conditions arise: large displacements at the supported ends and high stress levels. As mentioned earlier, the situation may be solved by stiffening the gate by adding either transverse, longitudinal of both types of stiffeners.
The maximum stress in a radial gate [17] can be estimated as:
where 𝑘 is a dimensionless parameter that depends on the ratio 𝑏/𝑎 and on the boundary conditions ( 𝑘=25 [18]), 𝑝 is the hydrostatic pressure at the middle of the gate, 𝑡 is the plate thickness and 𝑎 and 𝑏 are the minimum and maximum spacing between stiffeners, respectively.
The maximum deflection of the radial gate can be determined as:
where 𝐸 is the Young’s modulus and 𝜉 is a dimensionless parameter that depends on the dimensions of the gate (see Table 4). For this specific case, 𝜉 was assumed equal to 0.0284.
Eqs. (5) and (6) provide the maximum values for stresses and displacements, respectively. After substituting the corresponding values into these formulas, a maximum stress of 𝜎 𝑚𝑎𝑥 =200 MPa and a maximum deflection 𝛿 𝑚𝑎𝑥 = 5.5 mm are obtained for the considered gate. It must be mentioned that these values represent operational conditions.
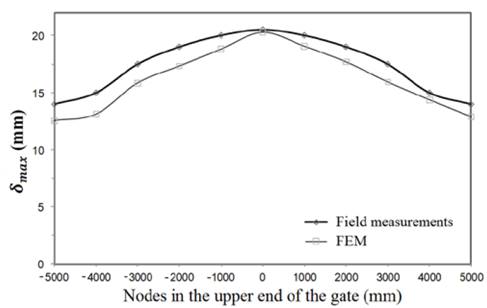
Fig. 15 shows the displacement profile at the upper end of the gate. Note that a good agreement is obtained between the numerical results and the actual measurements [20]. From a practical point of view a maximum displacement of 22 mm means that the gate is leaking as such displacement goes beyond the allowable value of 5.5 mm.
Taking into account that the maximum stress and the maximum displacement control the integrity of the gate and keeping in mind that the current design allows greater values for these parameters, it is necessary to solve this situation by adding stiffeners. Then, a parametric analysis using a simplified finite element model is conducted in order to reduce the maximum stress and the maximum displacement in the gate. In the simplified model, the arms are correspondingly substituted by a fixed boundary condition.
In general, the flexural rigidity of the stiffener, 𝛾 𝑠 , is used to describe the capacity of a stiffener to resist buckling and control lateral deflection. Usually, this rigidity is expressed relative to the plate stiffness, 𝐷, as follows:
where 𝐷=𝐸 𝑡 𝑤 3 /12 1− 𝜈 2 is the flexural rigidity of a unit width of the web plate. The flexural stiffness for the IPN profiles is also listed in Table 2.
Fig. 16 shows the maximum displacements and stresses attained for the radial gate with stiffeners in both directions. These results are presented for the gate stiffened with IPN100 (Figs. 16a and 16b) and IPN300 (Figs. 16c and 16d). The distribution of the stiffeners was even in both directions. There is a reduction in the out-of-plane displacements of the gate after increasing the number of stiffeners, as well as after increasing the size of the stiffener. Similar results are observed for the maximum stresses. All the structural elements (plate and stiffeners) are subjected to bending, therefore an increase in the second moment of area of the stiffener leads to redistribution of the stresses in the gate, attaining a significant reduction.
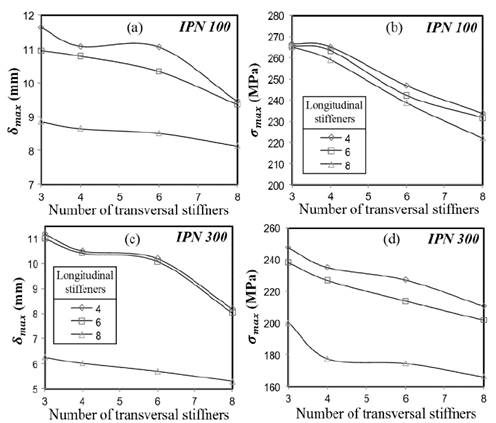
Source: The authors.
Figure 16 Maximum von Mises stress and maximum displacement at the supported ends from numerical simulations for profiles IPN 100 and 300.
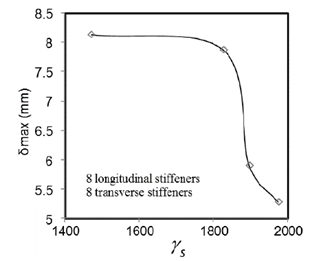
Fig. 17 shows the maximum displacements for the gate with 8 longitudinal and 8 transversal stiffeners. It is observed that an increasing flexural rigidity reduces the out-of-plate displacements. Comparing these results with the maximum allowable displacement found from Eq. (6) ( 𝛿 𝑚𝑎𝑥 = 5.5 mm) it is seen that the IPN300 stiffener is the only one capable of reducing the displacements below this limit.
4. Summary and conclusions
This paper has presented a numerical study on the elastic behavior of stiffened curved plates subjected to transverse loading; a parametric analysis to evaluate the beneficial effects of including longitudinal and transverse stiffeners; and the application of the proposed methodology to the specific case of radial intake gates in a hydroelectric power plant. The computational model was validated with analytical solutions available in the literature for flat and curved plates and by comparing it with a case history concerning the response of a hydroelectric power plant intake radial gate subjected to a hydrostatic head. It is shown that the static behavior of a curved plate subjected to hydrostatic head is a suitable way to size intake gates and define the maximum reservoir water level; and that stiffeners are a practical way to retrofit existing elements as they increase system stiffness and reduce transversal deformations, which are directly reflected in an improvement of system reliability and capacity to meet new power generation requirements.