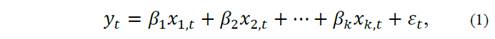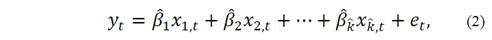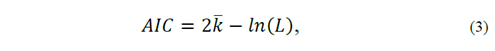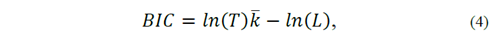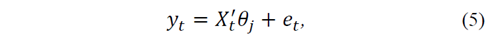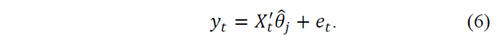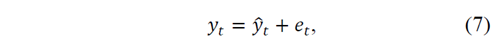1. Introduction
Forecasting and construction of operational scenarios is a key component of the appropriate functioning of any firm in the energy sector; it is crucial to project management and thus to decisions about the operational and financial viability of a given project. This is also true for companies with a business unit focused on exploiting renewable energy sources, such as photovoltaic energy conversion systems. Indeed, a correct assessment of operational risks, in terms of the energy that a firm could expect to offer to the market in a given day, is a crucial input when constructing cash flow scenarios and estimating returns on assets, liquidity ratios, present values, and other financial indicators. One can even make the argument that the execution of an entire energy conversion project depends on the accuracy of this exercise, and hence, it warrants considerable research efforts.
For the above reasons, the literature has explored several alternatives to forecasting the level of radiation a user can expect to be recovered by a photovoltaic system in a given period. These alternatives generally take into account the crucial relationship that exists between weather conditions and collected radiation, including the stochastic nature of the weather variables. For instance, [1] aim at forecasting radiation using k-th neighbor and interpolation methods, level of persistency, artificial neural networks, support vector regressions and time series analysis. These authors focus on the explanation of horizontal global radiation and use measures of radiation in a given location, alongside measures of weather variables in sparse locations around the radiation recording devices. [2] estimate an artificial neural network by genetic algorithms, aiming at forecasting daily radiation. They consider seven variables as inputs when training their network: average air temperature, minimum and maximum temperatures, relative humidity, atmospheric pressure, wind velocity and ground temperature. Using similar variables, [3] report that between three and four meteorological variables suffice to explain radiation, at least at the highest frequencies of their analysis. These authors base their conclusions on calculations of adjusted- R squared statistics, square residuals and forecasting errors. In contrast [4], employing similar methods and variables, finds that the best model includes all the available variables (seven in his case).
[5] estimate Multivariate GARCH models (time series models with autoregressive patterns in the conditional variance process), which include climatological variables such as solar brightness, precipitation, average minimum and maximum air temperatures, relative humidity and saturation deficit. [6] emphasize the importance of the range between the maximum and minimum temperatures when forecasting radiation, and they also highlight the changing nature of the relationship between radiation and weather variables, very likely driven by the strong seasonal patterns that characterize the latter.
In this study we do not focus on the point-forecast of radiation in a given period, instead we emphasize the construction of operational scenarios for an energy project in terms of the radiation that a photovoltaic unit can expect to collect, under certain weather conditions, in a given period, with an appropriate level of confidence. This enriches the tools available for energy project administrators and allows the unit in charge to make more accurate decisions, based on richer information, about a project’s realization or continuation.
Our methodology aims at providing thresholds of minimum radiation that one may expect to observe given certain weather parameters and for a desired confidence level. That is, we focus on the estimation of a specific quantile of the distribution of radiation conditional on weather variables, which increases the accuracy of our estimates. We explore several weather indicators in our empirical exercise and work with daily averages of those, as has been done previously (for instance in [7]). Given the impaired evidence regarding the number of variables required to explain radiation [3,4], we performed an automatic search algorithm to determine how many and which variables should be included in an optimal model. Importantly, our methodology takes into account the dynamic relationship that exists between weather and radiation. The changing nature of the relation between weather and radiation has been mainly ignored so far. That is, strong evolving weather conditions may change the way
in which radiation interacts with temperature, wind, precipitation and other variables. Therefore, any model that is estimated under the assumption of a stable relationship among these variables may display spurious patterns, which may be avoided only by explicitly considering this possibility. Endogenous structural tests in time series analysis, such as the ones employed herein, are specially designed to address this challenge.
In what follows we present the proposed methodology, and we illustrate it using data from a company that manages photovoltaic energy conversion systems, located in Colombia. We present our empirical results in section 3, and we discuss the results and conclude in sections 4 and 5, respectively.
2. Materials and methods
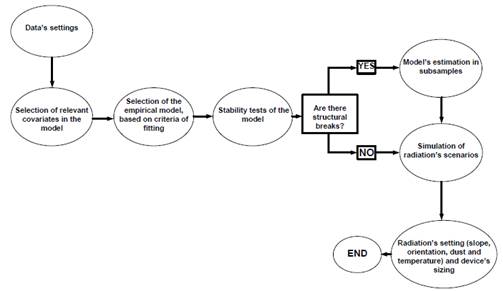
Our methodology focuses on the problem of estimating the expected global radiation on a horizontal surface, given a set of weather-related covariates. The proposal consists of five steps: i) selection of relevant variables to be included in the model, ii) selection of a parsimonious empirical model, iii) stability tests of the model’s parameters, iv) simulation of operation-scenarios, conditional on weather parameters and v) generation of the output variable to be included in traditional project management designs (see Fig. 1).
2.1. Selection of relevant covariates in the model
We assume a linear relationship1 between the total amount of radiation y t , and a set of weather-related covariates 𝑥 𝑖,𝑡 i=1,2,…k, . In our empirical implementation, we imposed a maximum possible number of covariates 𝑘 𝑚𝑎𝑥 =7, following data availability from regular records of a meteorological observatory. Working explanatory variables were: temperature, humidity, dew point, wind velocity, precipitation level, atmospheric pressure, and an indicator of cloudiness (the highest minus the lowest temperature within a day). In all cases, except for the last one, the recorded frequency of each variable was half an hour, and therefore we needed to transform the original series to daily averages to obtain standardized frequencies among all the covariates and the dependent variable2. This dependent variable was constructed as the cumulated level of radiation collected by the panel during the course of a day. We had measures of the level of radiation collected at half hourly intervals. These measures were aggregated by integrating out the area below the curve in Fig. 2 for each day within the sample.
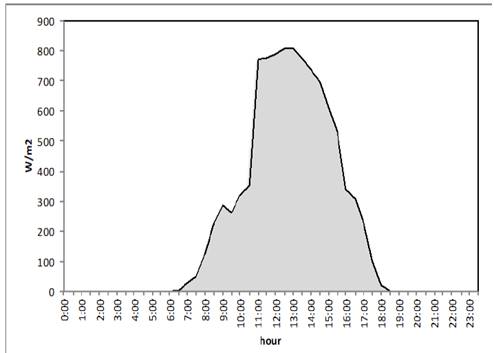
Source: The authors. Note: the Figure shows the level of radiation collected by a solar panel during each half- hour on a given day. The area below the curve corresponds to the total level of radiation collected by the solar panel. The data shown in the Figure was selected just for illustration purposes.
Figure 2 Radiation recorded on January 1st 2015
In this case, the population model that describes the relation between the collected radiation and the weather regressors can be written as follows:
In practice, we do not know coefficients 𝛽 𝑖 , nor do we know the value of k. That is, we must estimate the marginal effects of each covariate on the total amount of collected radiation, and, at the same time, we must decide how many and which variables may appear in eq. (1). Once this is done we end up with a sample-counterpart of eq. (1):
In eq.(2), marks over each of the coefficients indicate that those coefficients are related to the sample, instead of the population, and therefore they can be obtained from the data.
In the process of deciding which variables to include in eq. (2), we consider that redundant variables will conduce to inefficient estimations of the model’s parameters, while omitted (and relevant) variables will likely conduce to biased and non-consistent estimations. Hence, lacking a generally accepted theory regarding the shape and composition of eq. (2) led us to undertake a data-driven model selection process using ordinary least squares (OLS) and subsets of regressions. We conduced our exhaustive search for relevant covariates among subsets of variables typically recorded by meteorological observatories, many of which have been previously explored in the empirical literature.
Formally, given a maximum number of variables recorded by the meteorological observatory, 𝑘 𝑚𝑎𝑥 , we estimated different models fitted on subsets of variables, each of cardinality 𝑘 ≤ 𝑘 𝑚𝑎𝑥 . For each value of 𝑘 , which must be chosen a priori by the researcher, it was necessary to evaluate all possible combinations of covariates. Then, for each 𝑘 , we selected the model that minimized the sum of squared residuals, 𝑆𝑆𝑅= 𝑡=1 𝑇 𝑒 𝑡 2 .3 This strategy is equivalent to selecting the subset of variables for a given 𝑘 , that maximize the coefficient of determination, 𝑅 2 , of the linear projection of 𝑦 𝑡 onto 𝑥 1,𝑡 , 𝑥 2,𝑡 ,…, defined as 𝑅 2 =1− 𝑆𝑆𝑅 𝑆𝑇𝑆 , where 𝑆𝑇𝑆= 𝑡=1 𝑇 𝑦 𝑡 2 . There are several alternative approaches that may be used to accomplish this task. One that is widely accepted in the statistical literature, which, moreover, is available in the statistical software R, consists of conducing an exhaustive (forward or backward) search for the best subsets as explained in [8]. In practical terms, this can be done using the function ‘regsubsets()’, from the package ‘leaps’. In our implementation, we set 𝑘 =1…7 because our maximum number of variables was constrained by the number of variables available from the original observatory data.
2.2. Selection of the empirical model, based on criteria of fitting and parsimony
Notice that the preceding step gives us the best linear model for each value 𝑘 . Nevertheless, in practice, the researcher also needs to estimate the optimum value of 𝑘 . That is, we must select the best model among those available, taking into account model’s parsimony considerations, by penalizing the inclusion of redundant variables in the estimations. That is, if a variable is to be included in a model, it must add to the model in terms of explanatory power more than it takes from it in terms of efficiency. To this end, we used two different criteria: Akaike’s Information Criterion (AIC) and a Bayesian Information Criterion (BIC)[9], defined as:
where 𝐿 is the likelihood of the model, 𝑙𝑛() stands for the natural logarithm, and 𝑇 is the number of time series observations in the sample. The best model minimizes either of these two criteria.
2.3. Stability tests of the model’s estimates due to weather conditions
With the best model determined, after steps 1 and 2 we test for parameters’ stability. In the case of photovoltaic energy conversion systems, this is a crucial step of the methodology because weather-related variables are known to exhibit strong seasonality patterns, which in principle may have a significant effect on the relationship between the covariates in the model and the collected radiation during the year. This is even more important when modeling weather variables for energy companies located in countries characterized by higher latitudes and markedly contrasting seasons.
To this end, we used endogenous structural break tests following [10,11]. These procedures offer a reliable strategy to identify changes in the relationship between the covariates and the explained variable. The multiple-breaks statistic is intuitively a set of Chow’s statistics [12], calculated using recursive regressions over subsamples of increasing lengths. Several candidates for breaks are selected using the biggest F-statistics for which the null hypothesis in the Chow tests (i.e., parameters stability) is rejected. Then, asymptotic (corrected) critical values are used to contrast the null of no-breaks.
If we define 𝜃 = 𝛽 1 , 𝛽 2 ,…, 𝛽 𝑘 and 𝑋 𝑡 = 𝑥 1,?? , 𝑥 2,𝑡 … 𝑥 𝑘 ,𝑡 eq.(2) can be rewritten as:
where 𝑗=1,…,𝑚+1 represent a given model regime. That is, if we have 𝑚 structural breaks in the model’s parameters, it allows us to estimate 𝑚+1 regimes (or ‘seasons’). To identify and estimate the model in eq. (5), it is necessary first to estimate the number and location of breaks. The general idea underlying Bai and Perron’s [10] algorithm consists of the following steps:
First, we estimate a model through recursive regressions, increasing the sample from ℎ∗𝑇 to 𝑇∗ 1−ℎ , where ℎ∈ 0,1 . The sample is divided into two sub-samples, in the period where 𝑅 2 of the global regression is maximized. We set ℎ=0.05.
Once this break point is determined, the same searching procedure is applied to each of the two sub-samples. The process continues to the point where either it reaches a maximum number of breaks determined a priori ( 𝑚 𝑚𝑎𝑥 =5 in our case) or to the point at which new break candidates are no longer statistically significant.
To conduct hypothesis testing about the significance of each break point, critical values provided by Andrews [13] and Hanssen [14] must be used to avoid the identification of spurious break estimates.
Once the numbers and locations of the endogenous breaks are known, it is possible to estimate eq.(6):
Notice that the model has different coefficients for each regime or season. Such coefficients are determined endogenously, provided 𝑗>1. Estimations like those described above are performed using the package ‘strucchange’ in the statistical software R.
2.4. Simulation of scenarios
The simulation exercises in our methodology take into account, by construction, the most relevant variables explaining radiation, such as structural changes associated with different weather regimes. Eq.(6) for each regime can be rewritten as:
where 𝑦 𝑡 = 𝑋 𝑡 ′ 𝜃 for a given 𝑗, which has been supressed to simplify notation. The sources of uncertainty in this case are 𝑦 𝑡 and 𝑒 𝑡 . In the former case, we may observe different arrangements of the meteorological variables relevant to the model, which may conduce to distinct scenarios of operation. In the latter case, uncertainty may arise from other variables not included in the model, which may potentially affect the operation. To take into account both sources of uncertainty, we generated different scenarios of operation 𝑆, conducting re-sampling with replacement in the series of 𝑦 𝑡 and in the series of 𝑒 𝑡 . Then, we aggregated the two generated series into a single series to formulate comprehensive scenarios of operation for 𝑦. This procedure is justified as long as 𝑦 𝑡 is orthogonal to 𝑒 𝑡 , which holds by construction in our case.
The final idea consists of estimating some order statistics of the simulated scenarios for 𝑦 𝑖 , 𝑦 𝑖 𝑖=1 𝑆 . These are percentiles of interest for the administrator in charge of the project decisions. For example, percentiles α∈ 0,1 close to 0 (α=0.01,0.05,0.10) may be interpreted as conservative scenarios for decision making.
2.5. Data
We use data from February 4th 2014 to October 26th 2015. The variable of main interest is radiation, which was constructed as explained in section 2.1 and in Fig. 2. As explanatory variables we used average daily temperature, humidity, dew-point temperature, wind velocity, precipitation level, atmospheric pressure, and the difference between maximum and minimum temperatures each day. All variables were collected at half-hour intervals, and all but the last one were averaged to work with a daily version of each. All data were taken from a meteorological observatory located in Colombia, latitude 3.4383 and longitude -76.5161. After transforming each variable, according to our requirements we ended up with a total of 580 days of observations. Fig. 3 depicts our variables, and in Table 1 we show the summary statistics of our sample. Fig. 3 also highlights two regimes in the sample, which were detected using structural breaks tests as explained above.
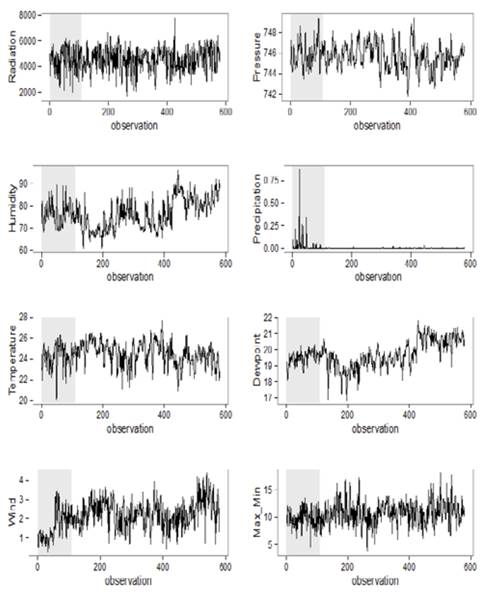
Source: The authors. Note: The Figure shows the daily averages of the variables employed in our estimations. Radiation is measured in kWh/m2, temperature is measured in °C, humidity is measured in %, dew-point temperature is measured in °C, wind velocity is measured in m/s, precipitation is measured in mm, atmospheric pressure is measured in Bar. Max-Min corresponds to the difference between the highest and the lowest temperatures registered each day. The shadowed area corresponds to the first regime in our sample, detected by using structural breaks tests.
Figure 3 Radiation and Explanatory Variables Used in The Analysis.
Table 1 Summary statistics of the variables used in the estimations.
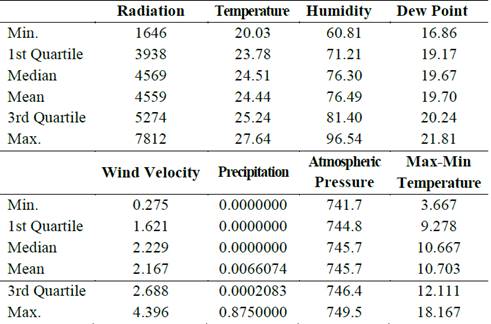
Source: The authors.
Note: Minimum, 1st and 3rd quartiles, median, mean and maximum for each variable.
Before conducting our estimations, we had to stabilize the mean of the atmospheric pressure variable using a dummy variable regression. We detected two changes in the scale of the series on March 31st 2014 and on October 5th 2015. These changes were unrelated to weather, but they were caused by settings in the measurement device.
2.6. Target
The procedure described above aims at sizing a photovoltaic system in an accurate fashion. We seek a suitable radiation value that could be used for sizing solar photovoltaic and photo-thermal panels, batteries, battery chargers and inverters. Applying the proposed methodology, we provide an option for performing sizing of these devices, which uses statistical tools for the selection of the level of radiation to be employed.
3. Results and discussion
Here we present the main results of our empirical implementation. First, we set the relevant variables to be included in our model. Given an optimal number of variables, the selected combinations are presented in Table 2. As can be seen, the difference between maximum and minimum temperatures appears in all selected models, using one to seven variables. The second most recurring variable is average temperature and the third is wind velocity. The least relevant variables, in terms of their significance in the models, are humidity and level of precipitation.
Table 2 Selected variables given k, from k=2 to k=7.
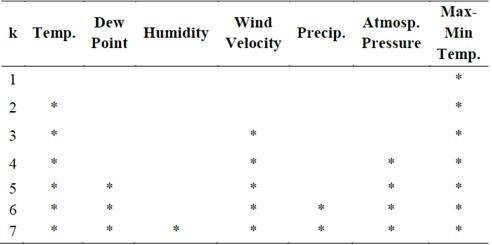
Source: The authors.
Note: An asterisk indicates that a given variable is included in the model with the number of variables indicated in the first column. The variables were selected using exhaustive (forward or backward) searches for the best subsets.
We estimated six models using the indications provided in Table 2. The models included between two and seven variables (we omitted the model with only one variable). Following the AIC criterion, the optimal model should include five variables, namely, average temperature, dew point temperature, wind velocity, atmospheric pressure and the differences between the max and min temperatures. According to BIC criteria, the optimal model should include only four variables, namely the same as those listed above except for dew-point temperature. In the interest of parsimony we followed BIC in the final specification (Table 3).
Table 3 Criteria for model selection.
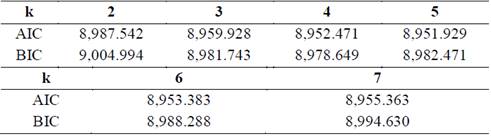
Source: The authors.
Note: Two criteria were used to determine the optimal number of variables in the model, the Bayesian Information Criterion (BIC) and the Akaike’s Information Criterion (AIC). The best models are those with lower values and are highlighted using bold type in each case.
Having selected the best model, we test for the stability of its parameters. We detected one statistically significant structural break in the sample that minimizes the BIC criterion (8914.26) when including partitions. The break is located on May 25th 2014 (day 110) with an associated 95% confidence interval between May 16th 2014 and June 1st 2014. Thus, we documented two different regimes in our sample, the first one from February 4th 2014 to May 25th of the same year, and the second one from May 26th until the end of the sample (see Fig. 1).
We present the estimated coefficients corresponding to the two detected regimes in Table 4. In the first regime, only two variables - temperature and the highest minus the lowest temperatures in a day - were statistically significant. Both of them exhibited positive signs in the regressions, meaning that an increase of one degree in the average temperature recorded in a given day increases the radiation collected by 342.44 kWh/m2. In the same line, an increase in the difference between the max and the min temperatures (i.e., indicating a less cloudy day) increases the supply of radiation by 364.68 kWh/m2, all other variables remaining constant. Although only two variables were significantly different from zero during this regime, the model is highly significant on a joint basis, as shown by an associated F statistic of 85.81, which is also significant at a 99% confidence level. The coefficient of determination, which is usually interpreted as a measure of a model’s goodness of fit, is relatively high, indicating that the estimated model accounted for 76.57% of the total variation in the collected radiation series.
Table 4 Coefficient estimates that relate each explanatory variable to radiation in each regime of the sample.
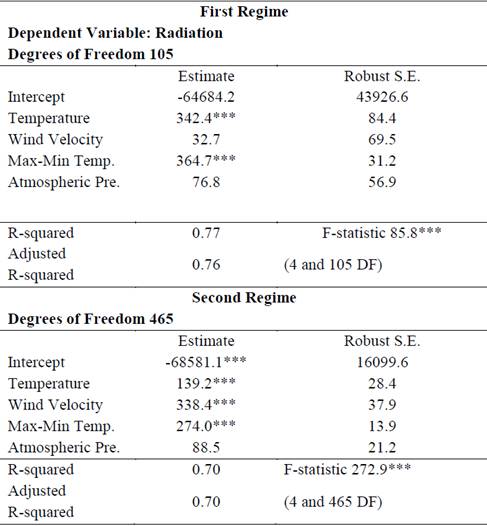
Source: The authors.
Note: * significant at 90% of confidence, ** significant at 95% of confidence, *** significant at 99% of confidence.
In the second regime, all the variables were statistically significant. Although, the two variables (temperature and max-min) continued to explain radiation in a significant fashion, their average effect on radiation was considerably less pronounced compared to the first regime. That is, with an increase of one degree in the average temperature, collected radiation increases by 139.15 kWh/m2 during the second regime (in contrast with 342.44 w/m2 in the first regime). The same holds true for the level of cloudiness. This means that during the second period of the sample, other variables, such as wind velocity and atmospheric pressure, were also highly relevant to explain the total level of radiation collected by a panel. Both variables have positive signs. These changes in the model were only possible to detect by testing the model’s stability by means of structural break statistics. This is a key point when modeling energy generation devices that depend on weather variables, especially when modeling renewable energies, which are characterized by strong seasonality patterns and are, therefore, very sensitive to structural instabilities associated with weather.
In Table 5 we report the expected operational scenarios at different levels of confidence from 5% to 90%. This information is valuable for project managers who seek to determine how much of their energy supply can be compromised for future delivery depending on the weather conditions. For example, during regime 2, the 5th percentile of the generated scenarios corresponds to 3,058.46 kWh/m2, this means that on only 5% of the days during a year (approximately 18 days) will the collected level of radiation be lower than 3,058.46 kWh/m2. Analogously, the 90th percentile is 5,685.84 kWh/m2, which tells us that on only 10% of the days will the collected radiation be higher than this level. Those scenarios can be interpreted as corresponding to ‘optimistic’ or ‘pessimistic’ expectations. The lowest quantiles are associated with very conservative scenarios of operation, and they can be used as forecasts of the worst scenarios a firm might face, during a particular weather regime, in terms of energy supply.
Table 5 Operation’s Scenarios
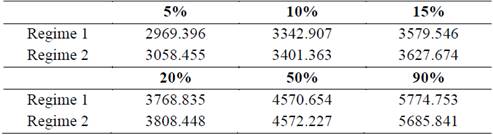
Source: The authors.
Note: The Table shows how much radiation we can expect the panel to collect, on a given day, during each regime in the sample, under certain levels of confidence. For example, in the second regime, we can expect that the collected level of radiation will surpass 5,685.841 w/m2 in a day only 10% of the time, while we can expect it to be lower than 3,401.363 w/m2 only 10% of the time.
Notice that the percentiles vary considerably from one regime to another. Specifically, they are almost always higher for the second regime than for the first regime. This seems quite natural because, during the first period of the sample, the observatory recorded more precipitation, lower dew-point temperatures, fewer differences between the highest and the lowest temperatures in a day (cloudier days) and a lower wind velocity (see Fig. 1). Nevertheless, when we focus on the 90th percentile during the first regime, the average level of collected radiation was lower compared to the second regime, but it was also more volatile. Therefore, we can conclude that the first regime of operation is also more risky in terms of the level of radiation that one may expect to receive in photovoltaic panels.
5. Conclusions
We propose a methodology for conducting simulations of operational scenarios for energy projects based on photovoltaic generation systems. It considers several documented facts about time series of weather, such as strong seasonality and structural breaks. Our proposal uses public weather time series, which are usually recorded by meteorological observatories. This makes our approach a suitable strategy for any firm interested in applying it to its own data and projects. We illustrate our methodology using data for a Colombian energy firm and we document that the difference between maximum and minimum temperatures appears in all selected models, using one to seven variables. The second most recurring variable is average temperature and the third is wind velocity. The least relevant variables, in terms of their significance in the models, are humidity and level of precipitation.