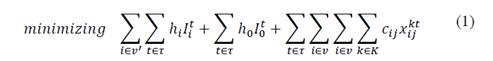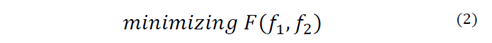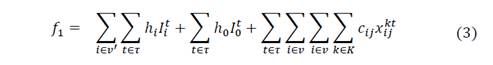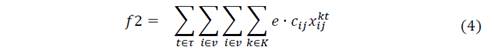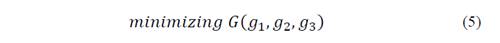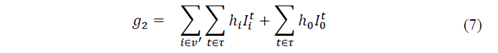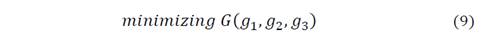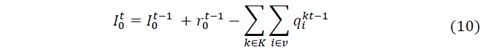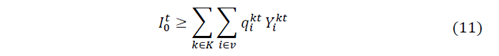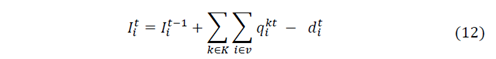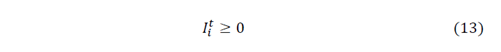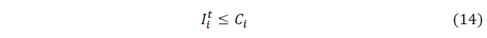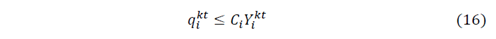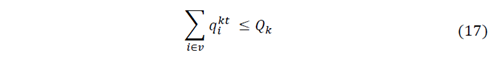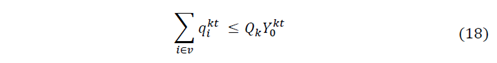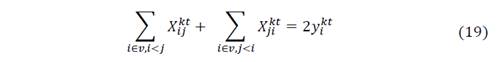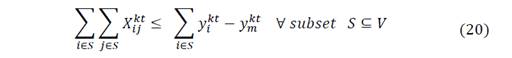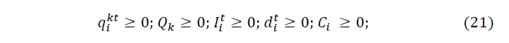1. Introduction
Transport processes in cities, regions and countries have increased due to new marketing processes generated by globalization and changes in consumers habits. These highly dynamic transportation processes generate high costs in organizations, which have been studied for many years and have usually sought for their optimization through models such as the Travelling Salesman Problem (TSP) or the vehicle routing problem (VRP). However, these transport processes not only generate economic impacts for companies, but also for society and cities, as it generates congestion and physical and chemical pollution. For that reason, practitioners in charge of these professional areas within companies and also academics must to continue with search processes looking for models that will improve both the economic and social/environmental conditions for companies and society.
Many authors have argued that collaboration among supply chain is one of the main strategies to reduce the cost of goods distribution, highlighting the Vendor Managed Inventory model -VMI as one of the more important ways companies can collaborate. Through VMI the inventory quantity can be optimized for multiple companies and from there to configure more efficient distribution systems, which effectively reduces the costs and the intensity of transport activities, as a result of a better allocation of inventory. This is the concept behind the Inventory Routing Problem -IRP optimization model, which, based on the collaborative inventory, allows transportation and inventory costs to be reduced simultaneously.
This paper analyzes the effect of the IRP model on the inventory and transportation costs of goods distribution, but also considering the effect of CO2 emissions, seeking to reduce the greenhouse gas emissions produced by the logistics activities. The impact on these variables was studied using three optimization processes: the IRP Model, a multiobjective model of IRP vs. CO2 emissions and finally a multiobjective model that contemplates the IRP background, but optimizing separately the inventory and transportation costs and also including CO2 emissions as a third objective function.
2. Inventory collaboration and optimization processes
Collaboration in logistics and supply chain is understood as the joint effort of several organizations seeking to obtain superior benefits to those that can be found separately. For this the companies cooperate in processes such as transportation, inventory management, storage, facility design, information exchange and other logistics activities [1-3]. Since many years supply chain collaboration has been developed through approaches such as Quick Response (QR), Efficient Customer Response (ECR), Continuous product Replenishment (CPR), Vendor Managed Inventory (VMI), Planning, Collaborative Forecasting and Replenishment (CPRF) and Centralized Inventory Management, among others [3-5].
According to Díaz-Batista and Pérez-Armayor [6], inventory collaboration in supply chains produces a lower total annual cost than when companies work individually, generating performance improvements in the entire supply chain [7-9]. The main problem lies in the allocation of inventory and transportation, which has been studied by multiple authors [10-12], for what the most used techniques are the VMI [13] and the IRP [14]. Through the IRP it is possible to simultaneously assign the inventory quantity and the routes to supply a set of customers that collaborate with one or several suppliers [14-17].
In the IRP model, the inventory is assigned to the customers in the planning periods and from there the routes are assigned to its supply [18-20]. For this, it is required that the supplier, who makes the supply decisions, know the information about customer demands, inventory levels and other parameters for the stock management and also the transportation process information, from which generates the routes are generated [21]. Campbell and Savelsbergh [22] studied the IRP model for long-term decision-making approaches, using a decomposition scheme of two-step decisions: in the first one the inventory is assigned and in the second the routes are generated. Other authors have performed schemes for the simultaneously allocation of inventory and routes generation [1,15,21].
The joint assignment of inventory and transportation can be performed using multiobjective optimization approaches, as it is made in the works of Pechlivanos [23], Chen and Lee [24], Liang [25], Liao et al. [26], Afshari et al., [27], Shankar et al. [28], Nekooghadirli et al [29], Andriolo et al., [30], Pasandideh et al., [31] and Pasandideh et al ., [32].
Both for the IRP or multiobjective solutions there are require heuristic and metaheuristic techniques. The most used heuristic and metaheuristic for solving these optimization problems are Simulated annealing, Genetic algorithms, Evolution algorithms, Evolutionary programming, Artificial immune system algorithm, Particle swarm optimization and tabu search [33,34].
Particularly, to solve multiobjective optimization models, the main methods are: MOGA (Multi- Objective Genetic Algorithm), NSGA y NSGA-II (Nondominated Sorting Genetic Algorithm), SPEA y SPEA2 (Strength Pareto Evolutionary Algorithm), PAES (Pareto Archived Evolution Strategy) y PESA (Pareto Envelope-based Selection Algorithm), MO-VNS (Multiobjective Variable Neighborhood Search), DEPT (Differential Evolution with Pareto Tournaments), MO-TLBO (Multiobjective Teaching-Learning-Based Optimization), MOABC (Multiobjective Artificial Bee Colony), among others [33,34-37].
3 Methodology
In order to analyze the impact of the distribution processes on greenhouse gas emissions, different distribution processes were designed from three mathematical optimization processes:
IRP Model.
Multiobjective analysis using as objective functions the IRP and the CO2 emissions.
Multiobjective model using the IRP background, but optimizing as separate objective function the inventory and transportation costs and also including CO2 emissions as a third objective function.
For the three optimization processes, the same parameters were used and two genetic algorithms were used for its development. The first is a genetic algorithm specially configured for the solution of the IRP model, which evaluates the jointly allocation of inventory and transport routes, as is presented in Arango et al. [21]. For the multiobjective analysis an algorithm based on the NSGA2 is used, similar to what is presented in [14,37,38].
The emission factor of a typical vehicle used for the urban goods distribution was used to analyze the effect of the CO2 emission. The vehicle corresponds to a VAN with an average city emission of e = 190 g of CO2 / km [39]. This parameter is multiplied by the number of kilometers traveled, in order to calculate the amount of CO2 gases emitted.
The objective function for the IRP model is presented in equation 1, subject to a set of constraints as formulated in [14,15,21,38].
The first term is the sum of the inventory costs, which is obtained by multiplying the holding cost h 𝑖 by the amount of product 𝐼 𝑖 𝑡 hold in every time t for every customer i. The second term is the inventory costs at the supplier facility represented with the sub index 0. Transport costs are calculated by multiplying the transport costs 𝑐 𝑖𝑗 of traveling from node i to j by the binary variable 𝑥 𝑖𝑗 𝑘𝑡 which is equal to 1 if the vehicle k travel from I to j in the period t and zero otherwise. The set v includes all the nodes of the problem and 𝑣 ′ only includes the customers’ nodes.
In the case of the multiobjective models, the formulation of the first model, in which the IRP costs and the CO2 are evaluated is presented in equation 2. In equation 5, the formulation for the multiobjective model separating transport costs, inventory and the CO2 emission is presented.
The Multiobjective model formulation separating transport costs, inventory and CO2 emission is:
Those objective functions are restricted to the following equations that assure the correct distribution process and correspond to the IRP Model constraints, according to Arango et al. [15] and Archetti et al., [16].
For an explanation of the restrictions, readers may refer to [15-16] and [18].
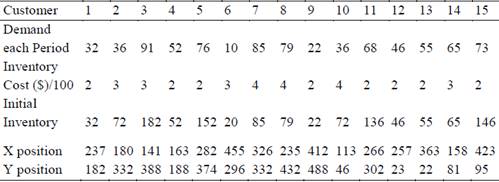
The input parameters are obtained from the instance of 15 customers and one supplier proposed by Archetti [16], increasing the amount of inventory that can be stored in each of the customers, as a strategy to produce better distribution costs and decrease the CO2 Emission. These parameters are presented in Table 1.
4. Results
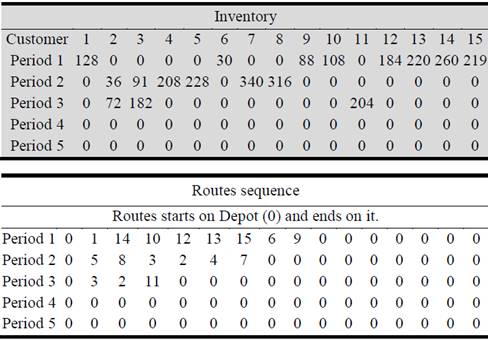
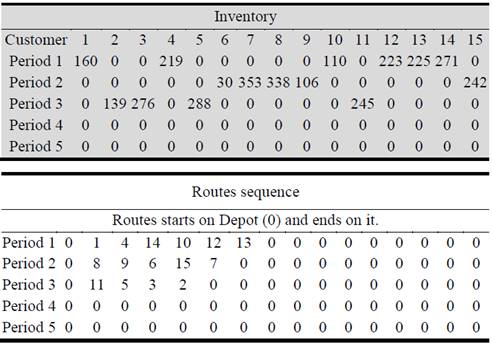
The IRP model, in which transport and inventory costs are added, generates a distribution process in which is not necessary to supply all the customers in all the periods. This produces a decrease in transport costs generated by an increase in inventory costs. The distribution plan that is generated from the best individual of the genetic algorithm used to solve the model is presented in figure 1. In the gray part is shown the inventory quantity that must be delivery to each of the customers, while in the unlabeled part the distribution sequence is presented.
This way, for period 1 only customers 1, 14, 10, 12, 13, 15, 6 and 9 should be served in that sequence. The quantities to be delivery are 128, 260, 108, 184, 220, 219, 30 and 88, respectively.
This distribution process generates a total cost of $ 2839.7, of which $ 468.2 correspond to inventory costs and produces a CO2 amount of 454.39 g.
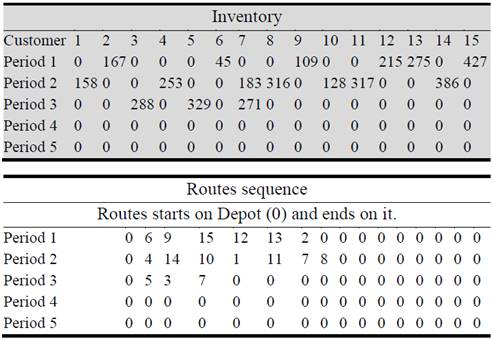
In the multiobjective model in which both the IRP costs and the CO2 emission are simultaneously optimized. A single optimal individual is produced, which is presented in figure 2. This result generates a cost of $ 2851.5, of which $ 463.9 are inventory cost and a CO2 emission of 453.6 g that is virtually identical to the solution generated by the IRP model. However, this solutions corresponds to a distribution system that assigns inventory and routes to customers in a different way than the IRP model does. For this reason, a slight decrease in CO2 emissions is generated, as a consequence of an increase in the distribution costs.
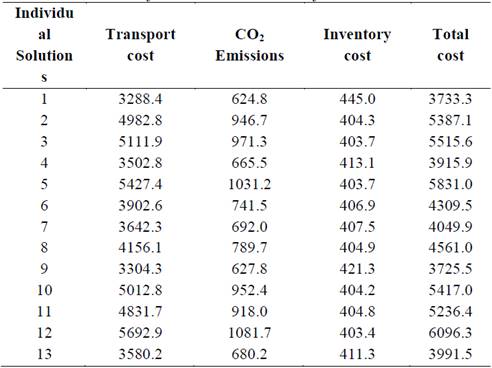
The multiobjective model, in which the transport, inventory and CO2 emission costs are analyzed separately, generates a set of individuals similar to those presented in figures 1 and 2. The set of individuals are produced by the non-dominance of the solutions, so it is not possible to argue that one solution is better than another and for that reason the decision maker, depending on his preference, can take any of the individuals solutions produced by the model. Table 2 presents the results for the 3 optimized objective functions, and includes a column adding the inventory and transport cost.
Table 2 shows that the values of total cost and CO2 emissions for each individual are higher than those reported in the solutions for the single IRP model and for the multiobjective IRP vs. CO2 emissions. However, inventory values in each solution are lower, with a behavior that the lower the inventory level the higher the transport cost and the CO2 emission, as a consequence of an increase in the transportation intensity in order to minimize inventory.
The behavior of the three-functions multiobjective model differs in its results to the previous models, since in the first the transport and inventory costs are added up, so in the optimization process the costs are compensated, while in the three-functions multiobjective model the algorithm must also look for which is the best solution that generates the minimum inventory costs without an excessively increase in transport costs. In order to compare these solutions, the problem was solved supplying all customers in each of the periods, what minimizes the inventory costs. For that, the Vehicle Routing Problem - VRP was used and solved with a genetic algorithm, for that the transport cost is $ 1722.5 for each period, which corresponds a total cost of $ 8612.5 for the 5 periods. This single VRP cost is higher than the transport cost for all individuals produced by the three-functions multiobjective model and becomes a non-optimal solution for the distribution process
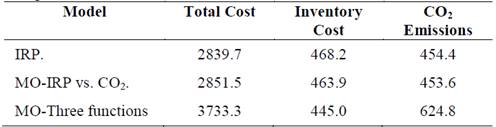
Table 3 presents the results of the three models. The individual solution one is selected for the three-function multiobjective model (presented in figure 3), which is the individual that generates the lowest CO2 emissions for that model.
From the results presented in Table 3, it is possible to observe that the total cost, inventory and CO2 emissions for the IRP and multiobjective IRP vs. CO2 are very similar, but differ with the solution that produced the fewer emissions in the three-function multiobjective model. This is caused by the reduction of the inventory costs, due to the three-function multiobjective algorithm generates solutions that somehow represent the best conditions for each of the objective functions, this way producing solutions with smaller inventory quantities but generating higher transport costs and CO2 emissions.
From this result, it is possible to infer that companies must make efforts in collaborative processes that allow to simultaneously reduce inventory, transportation and CO2 emissions, since a local optimum, as is the case of individual 1 of the three-functions multiobjective model, which generates the smallest inventory with a cost of 403.7, what is equivalent to a 13% reduction compared to the inventory for the IRP vs. CO2 emissions model, is also generating a 138% increase in CO2 emissions and a 114% higher distribution costs, which is not beneficial for both, companies or the environment.
5. Conclusions
Through inventory collaboration it is possible to reduce goods distribution cost for companies, but also to minimize the CO2 emission for these logistics activity, which contributes to the reduction of pollution problems in cities. Based on the results found in this paper, the search for the reduction of inventory costs in companies generates large increases in logistical costs as well as greenhouse gas emissions, which is not beneficial for Company nor the environment.
In this paper, the collaborative process through inventory and its effect on the pollutant gases emission are analyzed from different models, finding that it is better to use the IRP, which combines inventory and transport costs, than the three-function multiobjective model. This is because the multiobjective model, which seeks to simultaneously minimize transport, inventory and CO2 emissions, within its optimization process, must look for solutions that generate adequate relations between these three variables. This leads to the production of distribution plans that increase CO2 emissions and total costs, as a consequence of finding lower inventory cost, what is a local optimum that is not good for integral logistics.
As future research lines, it is recommended to use more objectives that are important for companies and customers, as it can be the service level. Other routing conditions are also important to be included in the presented models, as several suppliers, backhauls, dynamic conditions and multiple distribution levels. Finally it is interesting to include other logistics activities in the optimization process, as it can be warehousing and purchasing processes. These research lines allow to model more realistic situations and improve decision making in logistics activities.