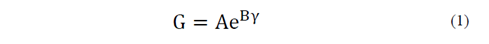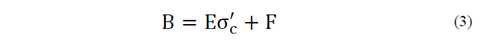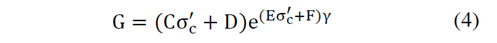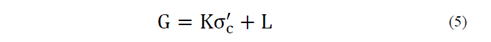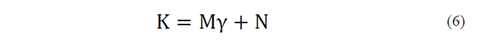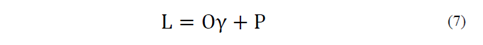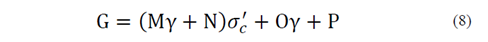1. Introducción
No cabe duda de que, a nivel mundial, la industria que más volumen de residuos produce es la minera. Por lo tanto, esta ha dado origen a un número no determinado de presas construidas por métodos hidráulicos y sin ningún tipo de compactación (presas de relaves), lo cual las hace susceptibles a presentar algún tipo de falla. Entre los factores detonantes de las fallas ocurridas en las presas de relaves se encuentran el grado de saturación de los residuos, el deslizamiento de los taludes, las solicitaciones dinámicas, la tubificación y la capacidad de carga del material de la cimentación [1].
Azam y Li [2] reportaron 198 casos de rotura de presas de relaves hasta el año 2000 y otros 20 de los años 2000 al 2010. De acuerdo con estos resultados estadísticos, se estima que la tasa de falla de las presas de relaves es del 1.2%, mientras que la tasa de falla de las presas de retención de agua convencionales es del 0.01% aproximadamente; es decir, más de dos órdenes de magnitud por debajo de la primera [1,2]. Esta situación ha dado lugar a la toma de conciencia de la necesidad de mejorar la seguridad en el diseño y operación de las presas de relaves, lo cual depende profundamente de las características de los materiales en condiciones estáticas y cíclicas, así como de las condiciones geológicas e hidrogeológicas del sitio de disposición [3].
Las propiedades del suelo que influyen en los fenómenos de pequeñas deformaciones incluyen la rigidez, el amortiguamiento, la relación de Poisson y la densidad. Sin embargo, las características más importantes de los suelos cargados cíclicamente son: el módulo dinámico de rigidez al cortante (G), el módulo dinámico de elasticidad (E), y la razón de amortiguamiento (ζ) [4]. La evaluación de las propiedades dinámicas es posible mediante una serie de técnicas de laboratorio y ensayos de campo, que se ajustan a rangos de deformación específicos, frecuencias de operación y velocidades de deformación tangencial.
En general, el ensayo de columna resonante es la técnica comúnmente más utilizada en el laboratorio para medir las propiedades dinámicas de los suelos a un nivel bajo de deformación [5]. Los diferentes diseños desarrollados someten a las probetas cilíndricas macizas o huecas a cargas armónicas axiales o torsionales, mediante sistemas electromagnéticos capaces de controlar con precisión la frecuencia y la amplitud de los diferentes tipos de onda que pueden generar.
La columna resonante (CR) fue utilizada por primera vez por Ishimato e Iida [6] y Iida [7,8] para ensayar suelos de Japón y casi dos décadas después por Bisshopp [9]. A partir de la década de los 60, la técnica se ha utilizado ampliamente en muchos países y ha sido sometida a numerosas modificaciones en lo que se refiere a las condiciones de restricción de la muestra. Wilson y Dietrich [10] utilizaron en su época uno de los equipos de columna resonante más novedosos en los Estados Unidos, con el que ensayaron muestras de arcilla. Hall y Richart [11] diseñaron y desarrollaron un equipo de columna resonante en el que las condiciones de restricción fueron “fixed - free”; es decir, fija en la base y libre en el extremo superior, el cual permitía inducir en las muestras de suelo vibraciones de tipo torsional y longitudinal. Drnevich et al. [12,13] desarrollaron un equipo en el que se utilizaban muestras cilíndricas huecas de suelo para determinar el módulo de corte y la relación de amortiguamiento a grandes deformaciones. La razón por la que utilizaron probetas huecas está relacionada con la dificultad de obtener un valor representativo de la deformación angular en las probetas macizas. Además, sustentaron la teoría en la que se basa la interpretación de los resultados obtenidos mediante la prueba de columna resonante. El principio de funcionamiento de un equipo de CR, las recomendaciones de calibración, el procesamiento de la información y la interpretación de resultados fueron descritos claramente por Drnevich, V. P. et al. [14].
En lo que respecta a la rigidez de los suelos granulares, investigaciones relevantes publicadas en la literatura destacan que el módulo de corte está influenciado fundamentalmente por la amplitud de la deformación cíclica, la presión de confinamiento, el índice de poros o relación de vacíos (e), el número de ciclos de carga, el grado de saturación, la frecuencia de la vibración, el índice de plasticidad, la historia de tensiones, la relación de tensión cíclica, la distribución granulométrica y la estructura del suelo [15-18]. Como producto de estas y muchas otras más investigaciones experimentales, en la literatura se reportan una serie de correlaciones empíricas para la evaluación del módulo de rigidez al cortante. No obstante, es importante resaltar que la validez de cualquiera de las relaciones propuestas está limitada a las condiciones bajo las que fueron desarrolladas (tipo de suelo, estado de tensiones, nivel de deformación, características de la vibración, entre otras). Sin embargo, para otros parámetros o condiciones este tipo de formulaciones pueden ser válidas o no.
Teniendo en cuenta los antecedentes citados anteriormente, el objetivo de esta investigación es evaluar, mediante la ejecución de ensayos de columna resonante, la influencia de la presión efectiva de consolidación y la magnitud de la excitación torsional, en la determinación del módulo de rigidez al cortante de dos tipos de materiales provenientes de los depósitos de estériles de las minas de Riotinto (Huelva - España). Además, se estudia la posibilidad de proponer funciones empíricas sencillas que correlacionen estos parámetros entre sí. La estructura del artículo incluye la descripción del equipo utilizado, la descripción de los materiales estudiados, el programa experimental ejecutado, el proceso de fabricación y montaje de las probetas en el equipo de columna resonante, el análisis de resultados y, finalmente, las conclusiones.
2. Descripción del equipo utilizado
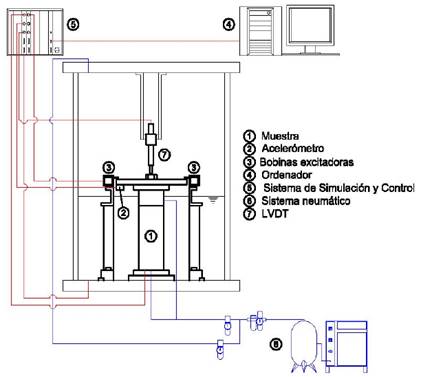
El equipo de columna resonante empleado durante la fase experimental de esta investigación fue fabricado por la compañía Wykeham Farrance, de Inglaterra. Se trata de un equipo instrumentado y automatizado que ofrece un conjunto de ventajas, dentro de las que destacan: (i) es un dispositivo combinado de columna resonante y corte torsional simple; (ii) calcula de manera automática la frecuencia de resonancia, la velocidad de propagación de las ondas de corte, el módulo de rigidez, la deformación angular y la razón de amortiguamiento; este último parámetro evaluado mediante la curva de decadencia de vibración libre, la cual daría una medida del amortiguamiento viscoso, o a partir del método de la media potencia (vibración forzada), cuyo resultado correspondería a un amortiguamiento histerético; (iii) no requiere del uso externo de osciloscopio, ni de generador de funciones; (iv) el sistema de excitación de estructura flotante interna permite realizar ensayos en los que las muestras pueden experimentar grandes deformaciones axiales durante la consolidación; y (v) permite visualizar, en tiempo real, la respuesta de los sensores durante la ejecución del ensayo. En la Fig. 1 se presenta un esquema ilustrativo del equipo.
Desde un punto de vista mecánico, el equipo de columna resonante se asemeja a un sistema de oscilación forzada con un grado de libertad, en el cual se hace vibrar una muestra de suelo dentro de un rango de frecuencias en el que se encuentra su primer modo natural. Una vez alcanzada la frecuencia de resonancia del material, y a partir de la teoría de propagación de ondas en medios elásticos continuos, es posible la evaluación de la velocidad de propagación de las ondas de corte (Vs) o compresión (Vp), según el tipo de excitación inducida (cargas armónicas torsionales o longitudinales), el módulo de rigidez al cortante (G), la razón de amortiguamiento (D), el módulo de Young (E), entre otros.
En este caso en particular, las condiciones de restricción de la muestra fueron “fixed-free”, es decir, que la probeta se mantenía fija en la base y libre en el extremo superior, y la vibración fue de tipo torsional.
El equipo consta básicamente de los elementos y sensores que se mencionan a continuación. 1) Dos células cilíndricas huecas de policarbonato que permiten, mediante la célula interior, aplicar la presión de consolidación a las probetas a través de un fluido, sin que los componentes electrónicos queden sumergidos, y, mediante la célula exterior, aplicar al fluido confinante la presión suministrada por un sistema de acción neumática. 2) Una base inferior a través de la cual se aplica la presión de cola o contrapresión y se permite el drenaje de las probetas durante la fase de consolidación. 3) una cabeza corrugada, sin posibilidad de drenaje, encargada de transmitir las acciones torsionales. 4) Un mecanismo impulsor compuesto por ocho bobinas y cuatro imanes encargados de aplicar la tensión torsional a la muestra. 5) Un acelerómetro adosado al mecanismo destinado a generar la acción torsional; el cual suministra la información necesaria para calcular la velocidad de propagación de las ondas de corte (Vs). 6) Un LVDT que permite medir las deformaciones axiales. 7) Dos transductores de proximidad que permiten medir las deformaciones angulares, en el caso de que no se utilice la información del acelerómetro para calcularlas. 8) tres transductores de presión destinados a medir la presión de Cámara (σc), y la presión de cola o contrapresión (Pc) y las presiones intersticiales (u). 9) Un transductor para registrar los cambios volumétricos durante la fase de consolidación. 10) Una unidad compacta dotada con una fuente de poder, un regulador de presión manual, dos electro-reguladores de presión, 8 componentes electrónicos de acondicionamiento de señal y un módulo de control y adquisición de datos. 11) Un computador que controla el equipo y adquiere los datos.
3. Descripción de los materiales
Los materiales utilizados en esta investigación fueron extraídos mediante la exploración superficial de los depósitos de estériles de las minas de Riotinto, las cuales se localizan en la zona centro oriental de la Provincia de Huelva (España).
En el sitio de la mina los materiales objeto de estudio se conocen bajo los nombres: Arena Cerro Salomón (ACS) y Lodos de alta densidad (LAD). De acuerdo con la identificación visual de las muestras representativas de ambos materiales, estos corresponden a una arena limosa gris de grano fino, en el caso de las ACS, y a una arena limosa gris verdoso de grano fino, en el caso de los LAD. La información relacionada con las propiedades índice de los materiales ensayados, se incluye en la Tabla 1.
En la Fig. 2 se puede observar el aspecto de los materiales en estado natural y una vez homogeneizada su humedad al ambiente de laboratorio.

Fuente: Elaboración propia.
Figura 2 Aspecto de los materiales provenientes de las minas de Riotinto. 1) detalle del sitio donde se tomó la muestra de arena ACS, 2) aspecto de las arenas ACS en estado natural, 3) aspecto de los LAD en estado natural, 4) aspecto de los LAD una vez homogenizados en laboratorio.
En la Tabla 1 se puede evidenciar que, debido a la composición mineralógica de los materiales ACS y LAD, los valores de gravedad específica obtenidos resultaron ser elevados comparados con los valores típicos reportados en la literatura para las arenas limosas. De acuerdo con Djoenaidi [19] y Bardet [20], la gravedad específica de sólidos de las arenas limosas puede ser del orden de 2.65.
Por otra parte, cabe anotar que los materiales investigados contienen elementos químicos tóxicos y nocivos para la salud; un ejemplo de ello es el Arsénico, que es fácilmente identificable por el fuerte olor a acido que expele durante el proceso de secado en estufa y, además, es el responsable de la coloración que toma el agua y los elementos que entran en contacto con el material. Otros datos de interés de los materiales investigados se pueden consultar en Martínez [21].
4. Programa experimental
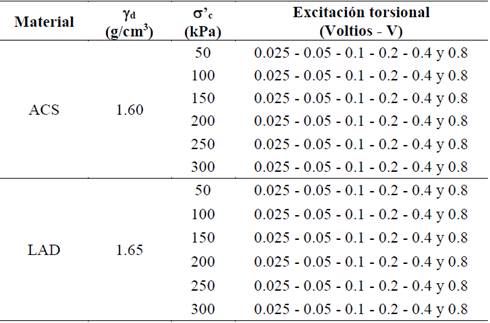
Con las muestras de los materiales ACS y LAD se realizaron los ensayos de columna resonante por barrido continuo, conducentes a la determinación de la frecuencia de resonancia (Fr) y el módulo de rigidez al cortante (G), de acuerdo a las condiciones generales que se incluyen en la Tabla 2.
Como se puede observar en la Tabla 2, dada una densidad seca predefinida, se programó la ejecución de las pruebas variando la amplitud de la señal de estimulación desde 0.025 Voltios hasta 0.8 Voltios, para cada uno de los estados de confinamiento indicados.
Las presiones “efectivas” de consolidación se establecieron dentro de un rango variable entre 50 kPa y 300 kPa, debido a que la capacidad máxima estable del compresor utilizado es de 750 kPa. La presión de cola o contrapresión aplicada en todas las pruebas fue igual a 400 kPa. Las dimensiones de los especímenes fueron H = 100.8 mm y D = 49.7 mm, cumpliendo así con una relación altura/diámetro igual a 2.03 y eliminando, por lo tanto, la incertidumbre relacionada con la esbeltez de las probetas. En total se realizaron 72 pruebas de columna resonante, debido a las combinaciones de los parámetros de ensayo (σ’c y V) para caracterizar dinámicamente los dos tipos de materiales.
5. Fabricación y montaje de probetas
Dada la necesidad de reproducir un buen número de probetas con densidades secas (γd) y humedades (w) iguales, se emplearon los accesorios incluidos en la Fig. 3, los cuales garantizan la homogeneidad entre ellas. Asimismo, debido al grado de dificultad que supone la fabricación de probetas con materiales arenosos, fue necesario recurrir al diseño y fabricación de accesorios, no tradicionales, que garantizan la verticalidad de la cabeza excitadora y el paralelismo de los extremos de las probetas. Dichos elementos pueden ser observados en las Figs. 4-8

Fuente: Elaboración propia.
Figura 3 Elementos necesarios para la fabricación de probetas: 1) molde tripartido; 2) abrazaderas; 3) guías cilíndricas, collarines o extensores de molde; 4) cilindros metálicos o pistones; 5) cilindro hueco bipartido
Los materiales que llegaron al laboratorio se secaron al aire y se mezclaron hasta lograr una humedad uniforme al ambiente del laboratorio. Después, fueron conservados en una cámara húmeda con los contenidos de agua mencionados en la tercera columna de la Tabla 1.
El procedimiento para la fabricación de las probetas, de los materiales ACS y LAD, se indica a continuación. 1) Cálculo de la densidad húmeda (γh), a partir de la densidad seca (γd) y conocida la humedad de homogeneización (wlab). 2) Preparación de la probeta con material homogeneizado, cuya cantidad es estimada con base en la densidad húmeda y el volumen del molde. 3) Colocación del molde tripartido abrazando la base inferior del equipo de CR y apoyado sobre un cilindro hueco bipartido (elevador de molde); el molde tripartido contiene en su interior una membrana de látex que se adhiere a este mediante la aplicación de vacío a través de un conducto lateral. 4) Colocación del material en el interior del molde, mediante compactación dinámica, en cinco capas de igual peso e igual altura. Para la compactación de la última capa se coloca un extensor de molde o collarín sobre el extremo superior del molde tripartido, para evitar la pérdida de material durante la compactación del suelo (Ver Fig. 4). 5) Colocación de un cilindro metálico, de igual altura a la del extensor de molde, sobre la última capa de material en estado suelto. 6) Compactación dinámica de la última capa hasta lograr que el cilindro metálico quede a ras con el collarín; de este modo se garantiza la densidad especificada. 7) Remoción del cilindro y el collarín que se utilizaron durante la compactación de la última capa (Ver Figs. 5 - 8) Colocación de la estructura porta cabeza excitadora, con el fin de asegurar la verticalidad de la cabeza excitadora durante el montaje de las probetas. 9) Colocación de la cabeza excitadora apoyada sobre la muestra y firmemente asegurada a la estructura portadora. 10) Remoción del vacío aplicado entre la membrana de látex y el molde tripartido e inundación de la probeta. Debido a que, en general, los equipos convencionales de columna resonante adolecen de drenaje superior a través de la cabeza excitadora, lo cual dificulta la saturación de las probetas por la imposibilidad de remover el aire atrapado tanto en el sistema como en el interior de la muestra, en esta investigación se le dio solución a este problema mediante el flujo lento ascendente, originado por acción de la gravedad. El flujo lento se mantiene hasta el momento en que empieza el goteo a través de la interface formada por la muestra y la cabeza excitadora (Ver Figs. 6. 11) Remoción del elevador de molde y sujeción de la membrana de látex tanto a la cabeza excitadora como a la base inferior del equipo de CR, mediante un par de sellos “O’-Rings”. 12) Aplicación de vacío al interior de la probeta. El objetivo de aplicar vacío, a través del drenaje inferior, es garantizar la estabilidad de la probeta mientras se completa el proceso de montaje del equipo. 13) Remoción de todos los accesorios utilizados para la fabricación de las probetas (Ver Figs. 7. 14) Colocación de la célula triaxial interior que sirve de soporte al sistema excitador. 15) Instalación del sistema excitador. 16) Instalación de los transductores de proximidad y del LVDT destinado a medir las deformaciones axiales. 17) Conexionado de los transductores de presión y cambio volumétrico. 18) Finalmente, montaje de la célula triaxial exterior (Ver Fig. 8).

Fuente: Elaboración propia.
Figura 4 Fabricación de muestras cilíndricas de arena mediante molde tripartido y compactación dinámica (pasos 1-4).

Fuente: Elaboración propia.
Figura 5 Compactación de la última capa de material para garantizar la densidad predefinida (pasos 5-7).

Fuente: Elaboración propia.
Figura 6 Montaje de la cabeza excitadora sobre la muestra de suelo e inundación de la misma (pasos 8-10).

Fuente: Elaboración propia.
Figura 7 Sujeción de la membrana de látex a la base inferior del equipo y a la cabeza excitadora mediante “o-rings” y remoción de todos los accesorios utilizados (pasos 11-13).
6. Resultados y análisis
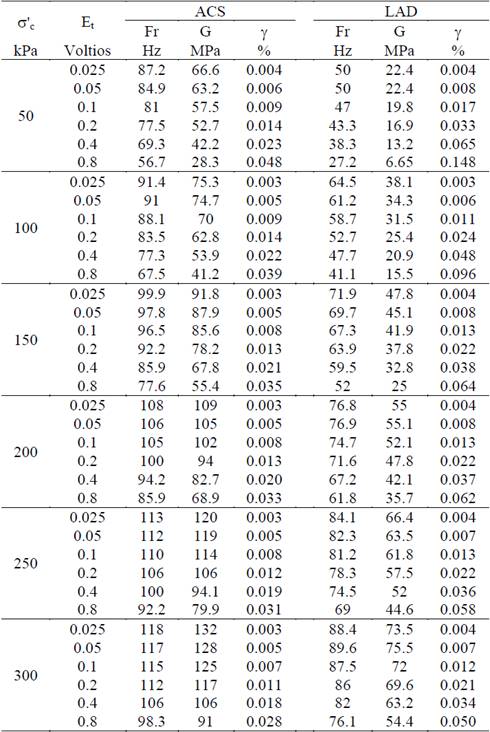
Los resultados de las 72 pruebas de columna resonante se incluyen en la Tabla 3. La información contenida en la Tabla 3 permite evaluar, para cada uno de los materiales estudiados (ACS y LAD), la influencia de factores como la presión efectiva de consolidación (σ’c) y la deformación angular unitaria (γ) en la determinación del módulo de rigidez al cortante (G).
Además de presentar un análisis cualitativo de los resultados, el análisis está orientado hacia la obtención de funciones empíricas que permitan reproducir los resultados experimentales obtenidos a través de las pruebas de columna resonante. No obstante, conviene resaltar que estos resultados son válidos fundamentalmente dentro de los rangos de deformación angular experimentados por cada uno de los materiales (de 0.003 a 0.048% en el caso de las ACS y de 0.003 a 0.148% en el caso de los LAD). Por lo tanto, si se quiere estimar el comportamiento dinámico de los materiales ACS y LAD bajo condiciones de ensayo que están fuera de los rangos de deformación mencionados previamente, es necesario calibrar nuevamente las funciones empíricas en un plan de ensayos complementario al de esta investigación.
6.1. Módulo de corte vs deformación angular
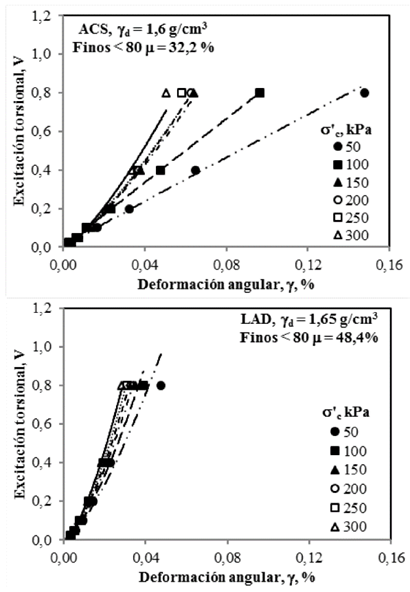
Como se ilustra en la Fig. 9 la deformación angular experimentada por los materiales ACS y LAD se incrementa en la medida en que aumenta el nivel de excitación torsional [22]. Los resultados siguen una trayectoria de tipo potencial con un coeficiente de correlación cercano a uno (R2(1). Asimismo, puede observarse que independientemente del valor de la excitación torsional, la deformación angular disminuye en la media en que aumenta la presión efectiva de consolidación.
Los valores de deformación angular representados en la Fig. 10 corresponden a la deformación angular media (γm) evaluada como 2γmáx/3; donde γmáx es la deformación angular máxima medida por el acelerómetro.
Fuente: Elaboración propia.
Figura 9 Tendencias de variación de γ en función del nivel de excitación torsional. para diferentes valores de σ’c y tipos de material.
Fuente: Elaboración propia.
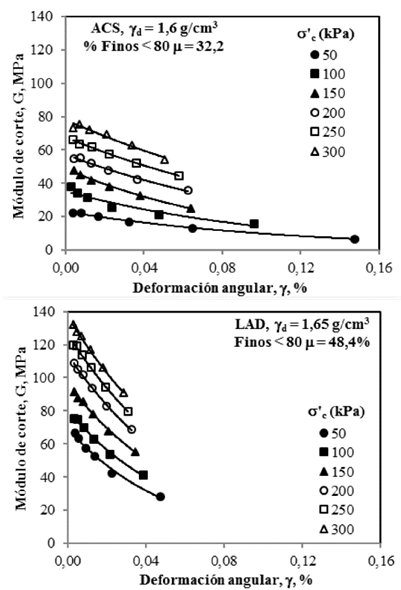
Figura 10 Tendencias de variación de G en función de γ para diferentes presiones efectivas de consolidación y tipos de material.
La Fig. 10 ilustra, para cada uno de los materiales, las tendencias de variación del módulo de rigidez al cortante (G) en función de la deformación angular (γ) bajo diferentes presiones efectivas de consolidación (σ’c). De la Fig. 10 se deduce que independientemente del tipo de material estudiado y de la magnitud σ’c el valor G tiende a disminuir con el incremento de γ. Por ejemplo, para un valor de σ’c = 100 kPa, la degradación de G en los materiales ACS y LAD es del orden del 28% y 48%, respectivamente, cuando γ se incrementa del 0.003% al 0.04%. En el material ACS, la influencia del nivel de deformación en la degradación de G, disminuye con la reducción de la presión efectiva de consolidación.
Por otra parte, teniendo en cuenta que el material ACS es el constitutivo del material LAD y que ambos materiales fueron ensayados bajo iguales condiciones de excitación torsional (nivel de deformación) y de presión efectiva de consolidación, se encontró que el incremento del contenido de finos y de la densidad seca influyen significativamente en la evaluación de G; puesto que a iguales valores de γ y σ’c, el valor de G en el material LAD resulta ser casi el doble del correspondiente al material ACS. No obstante, la tasa de degradación de G es mucho más alta en los LAD.
Independientemente del material estudiado y de la presión efectiva de consolidación, la degradación de G en función de γ sigue aproximadamente una tendencia de tipo exponencial con muy baja dispersión. Lo anterior pone en evidencia la no linealidad del comportamiento tensión - deformación dentro del rango de deformaciones angulares experimentado por cada uno de los materiales. Con base en la deducción anterior, para cada valor de σ’c, es posible establecer una relación exponencial entre el módulo de corte y la deformación angular (γ) de la forma:
Donde G es el módulo de corte en MPa, ( es el nivel de deformación en porcentaje y A y B son constantes empíricas que dependen de σ’c. Debido a que las tendencias de variación de las constantes A y B en función de σ’c son similares en ambos materiales, en la Fig. 11 se muestran únicamente las tendencias correspondientes al material LAD. De esta manera, de la Fig. 11 se deduce que la variación de las constantes A y B en función de σ’c siguen aproximadamente tendencias lineales que se pueden expresar como:
Al reemplazar las eq. (2)-(3) en la eq. (1) se tiene:
Donde σ’c está en kPa; ( en porcentaje y C, D, E y F son las constantes que resultan de las regresiones lineales. En la Tabla 4 se incluyen los valores de las constantes para los diferentes materiales.
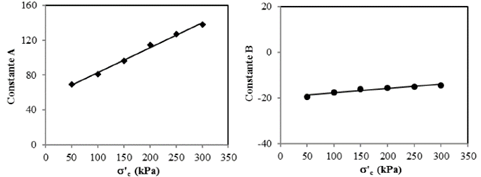
Fuente: Elaboración propia.
Figura 11 Variación de las constantes empíricas A y B en función de la presión efectiva de consolidación para el material LAD.
6.2. Influencia de σ’ c en el módulo de corte
Con el fin de evaluar la variación del módulo de corte en función de la presión efectiva de consolidación, para diferentes niveles de deformación angular, se procedió a calcular G a partir de la eq. (1) mediante la sustitución de las constantes A y B por los valores correspondientes a cada estado de confinamiento y tipo de material. La Fig. 12 representa los valores obtenidos de G en función de σ’c, para diferentes niveles de deformación angular.
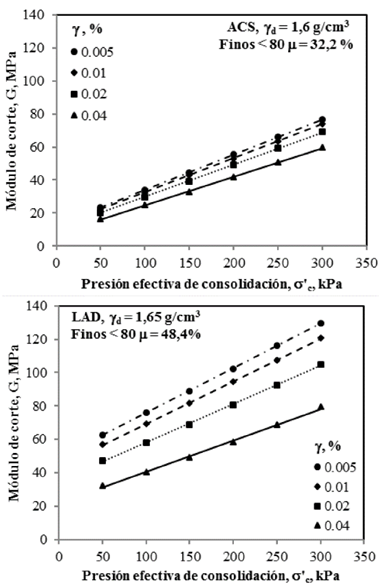
Fuente: Elaboración propia.
Figura 12 Tendencias de variación de G en función de σ’c para diferentes niveles de deformación angular y tipos de material.
De la Fig. 12 se deduce que independientemente del tipo de material ensayado y del nivel de deformación angular G resulta severamente afectado por la reducción de σ’c. La influencia del incremento de γ en la degradación de G, tiende a ser más importante para valores altos de la presión efectiva de consolidación.
Independientemente del tipo de material y del nivel de deformación angular la variación de G en función de σ’c sigue aproximadamente una tendencia de tipo lineal con muy baja dispersión. Lo anterior se puede expresar como:
Donde G es el módulo de corte en MPa; σ’c la presión efectiva de consolidación en kPa; K y L son constantes empíricas que dependen de la deformación angular. Debido a que las tendencias de variación de las constantes K y L en función de γ son similares en los dos materiales estudiados, en la Fig. 13 se incluyen únicamente las tendencias correspondientes al material LAD.
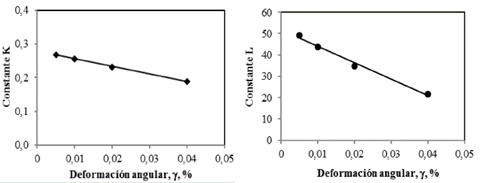
Fuente: Elaboración propia.
Figura 13 Variación de las constantes empíricas K y L en función de la presión efectiva de consolidación para el material LAD.
De la Fig. 13 se deduce que la variación de las constantes K y L en función de γ sigue aproximadamente tendencias lineales [23] y se pueden expresar como:
Al sustituir las eq. (6)-(7) en la eq (5) se tiene:
Donde γ está en %; G en MPa; σ’c en kPa; M, N, O y P son las constantes que resultan de las regresiones lineales. En la Tabla 5 se incluyen los valores de las constantes obtenidas para los diferentes materiales.
7. Conclusiones
Las conclusiones derivadas de este estudio son producto de un amplio programa experimental realizado con materiales provenientes de los depósitos de estériles de las minas de Riotinto, ubicadas en la Provincia de Huelva - España. Se realizaron 72 ensayos de columna resonante sobre muestras reconstituidas de los materiales ACS y LAD, con el fin de estudiar la influencia de parámetros como la presión efectiva de consolidación (σ’c) y el nivel de deformación angular (γ) en el módulo de rigidez al cortante (G) bajo deformaciones angulares que varían entre 0.003 y 0.148% y presiones efectivas de consolidación 50, 100, 150, 200, 250 y 300 kPa. Las conclusiones derivadas de la investigación son las siguientes:
A pesar que los materiales estudiados tienen un contenido de finos (< 80μ) alto, variable entre el 32% y el 48%, las arenas Cerro Salomón (ACS) y los lodos de alta densidad (LAD) se clasifican como una arena de grano muy fino a medio. Lo anterior en razón que los finos menores de 400μ no son plásticos; seguramente debido a que estos son generados durante el proceso de explotación de las minas y no como consecuencia de la alteración o la meteorización de la roca madre. Los materiales investigados se caracterizan por tener una gravedad específica alta y variable entre 2.99 y 3.02, lo cual puede deberse a la presencia dominante de elementos pesados como hierro, silicio y azufre.
Se evidenció que, sin importar el tipo de material y el valor de la presión efectiva de consolidación, la frecuencia de resonancia y el módulo de rigidez al cortante tienden a disminuir en la medida que se incrementa el nivel de excitación torsional (nivel de deformación).
Se encontró que para los dos tipos de materiales y las diferentes presiones efectivas de consolidación, la variación de la frecuencia de resonancia y del módulo de rigidez en función de la deformación angular describen una tendencia de variación de tipo exponencial con coeficiente de correlación (R2) prácticamente igual a la unidad.
Independientemente del tipo de material estudiado y del nivel de deformación angular, la variación de G en función de σ’c, sigue aproximadamente una tendencia de tipo lineal con muy baja dispersión.
Mediante la combinación de regresiones matemáticas es posible proponer funciones empíricas para el módulo de corte en función de la presión efectiva de consolidación y la deformación angular.