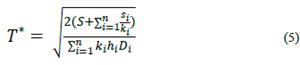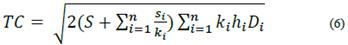1. Introduction
The urban goods distribution processes play a fundamental role in the competitiveness of companies and cities, since these activities generate logistics costs and are carried out in conditions in which goods transport interacts with passenger movement and other transport processes required in the city [1]. The intensity of the distribution process and the infrastructure constraints for vehicle mobility in urban areas usually increase the difficulties for goods transportation, evidenced in bottlenecks and in mobility restrictions imposed by city administrations, seeking to improve people's quality of life and mitigate negative impacts to the environment, such as greenhouse gases emissions [2].
In this way, it is necessary that companies propose new goods distribution processes and strategies for urban environments, pursuing several objectives, such as economic attractiveness for companies and the reductions of negative effects such as traffic congestions and chemical contaminants emissions [3]. Several strategies have been proposed by different authors and city administrators, as the implementation of city logistics platforms, the establishment of exclusive zones for goods transportation, information technologies application and time windows for trucks, among many others [4-6].
In order to generate better distribution processes, companies frequently concentrate their efforts in developing new advanced algorithms for goods transport [1], leaving aside two fundamental concepts: first, transportation is carried out by the need to distribute the inventory; and second, through collaboration between different actors, it is possible to generate synergies among several companies [1,3].
This article proposes a collaboration approach that allows generating joint supply plans for several products of different customers, seeking to reduce logistics costs and the number of trips required in the replenishment process. This collaborative approach enables to propose logistics replenishment plans which are attractive and easily applicable by companies, and also helps to mitigate the negative impact of logistics processes within cities, since reduction of the number of trips diminishes congestion and environmental pollution [7].
The proposed collaboration model is based on the joint replenishment problem - JRP, in which a group of customers replenish their products from a single supplier and share the required information for making the supply plans and the determination of the inventory allocation. The information is managed by the supplier following the Vendor Managed Inventory strategy. The supplier is responsible for assigning the collaborative replenishment and the distribution plans. The model is validated with the simulation of a logistics network composed by a single supplier and several customers, from which it was possible to observe a total inventory costs reduction as well as a decrease in the number of trips, compared to the case when the supply plans are made individually by each customer.
2. Collaboration in urban goods distribution
Collaboration between companies has a high potential in the supply chain [8] since it allows generating synergies between different organizations to reduce operating costs, increase flexibility [9], reduce stock amounts, increase capital turnover and produce better demand forecasting processes [10]. Several authors argue the importance of looking for new ways of carrying out goods distribution processes in urban environments [11-13] that can be economically attractive for companies and that can also reduce the negative impacts of transportation processes within cities [3,7]. Collaboration between actors is one of the most promising strategies in supply chain [1]. This is highlighted by [14,15], which mention the necessity to intensify collaboration between companies involved in the urban goods distribution processes.
The collaboration processes reported in the scientific literature are differentiated by the nature of the actors involved, considering, on the one hand, the collaboration between government and private actors and, on the other, the exclusive collaboration between companies (freight companies, cargo generators). The main collaboration interest between administrators and private companies is to organize the flow of goods through specific areas in the city, which is frequently achieved through mobility restrictions and the implementation of specialized infrastructure to improve transport processes, such as city logistics platforms, dedicated roads to cargo transportation and restricted parking and unloading areas [14]. The use of information systems that allow exchanging city information between the goods distribution actors is another way to encourage collaboration between companies and city administrators [16-18]. Exclusive collaboration between companies for urban goods distribution can be defined as the process in which several companies share vehicles, infrastructure or information, with the aim of reducing logistics costs and the negative effects of goods distribution within cities [19]. Collaboration for defining inventory plans is one of the most used strategies to achieve the mentioned goals [1,3,7,13].
Collaboration in inventory planning can be framed inside information sharing and there are several proposed strategies that support companies to incorporate this collaborative approach such as joint orders [20], efficient customer response (ECR) [21,22], collaborative planning, forecasting and replenishment (CPFR) [23], Just in Time [24], vendor managed inventory (VMI) [25-27], consignment stock [28], among others. The VMI and the CPFR approaches are the most popular collaborative approaches used to achieve cost benefits for companies [29]. A key element for the success of collaborative approaches in the supply chain is information sharing, as well as the role definition of the actors involved in such collaborative strategies [29]. In VMI the information of sales and inventory level is shared from customers to the supplier, who is in charge of defining the replenishment decisions and plans for the customers [26,29].
Several authors argue the importance of including inventory management decisions in goods distribution processes [30,31] since the intensity of transportation is a consequence of the inventory quantity required to be transported; e.g., the more cargo must be delivered, the more number of trips required [1]. Some authors who have integrated inventory and transport decisions in urban goods distribution processes through collaboration are [30,32,33].
3. Joint replenishment
In the scientific literature it is possible to find several inventory models that allow companies to carry out the joint replenishment of many products, making it possible to decide the optimal quantities to be ordered from a single supplier or multiple suppliers [34]. One of these models is the Joint Replenishment Problem (JRP), through which it is possible to determine the replenishment policy of different products from the same supplier, seeking to reduce the total replenishment cost that includes stored products, performing orders and stock-outs costs [35].
The JRP allows grouping different products that need to be ordered, which better distributes the fixed ordering costs among all the products [36], achieving cost savings in the total replenishment process. This reduction is reported by [37], indicating that using the JRP can save up to 13% compared with the individual inventory costs optimization for each product, using the economic order quantity (EOQ) model.
There are two strategies to find solution to the JRP model, which differ from the way in which the products are grouped: The Direct Grouping Strategy - (DGS) and the Indirect Grouping Strategy (IGS) [34]. In the Direct Grouping Strategy, the products are organized in several groups and each one has a different cycle time assigned in which the products are jointly ordered to the supplier. The products are ordered when the cycle time is reached. In the Indirect Grouping Strategy there is not a cycle time for each group of products to be ordered; instead, there is a unique cycle time and the products are ordered in integer multiple times of such cycle time. This multiple number indicates the moment in which every product must be ordered, thus the products with the same cycle time are always ordered together. The products with a cycle time equal to one must be ordered every cycle time and the other products must be ordered every two cycles, every three cycles, and so on. [34]. Several authors mention that the IGS produces more efficient results in terms of cost than the DGS [35-38].
In its simplest version, the JRP model seeks to optimize only the ordering and holding inventory costs at the customers' facilities. However, there are several variations to the original JRP model that consider elements such as capacity and resource constraints [36], dependent ordering costs [39], stochastic and dynamic demands [37], multi-level supply processes [37, 40] and inventory-routing problems (Joint Replenishment & Delivery Problem - JRD) [41-46].
4. Joint orders collaborative approach
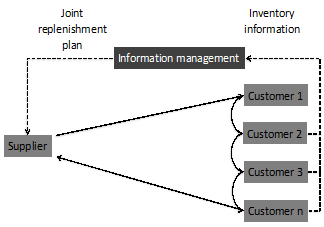
This article presents a collaborative approach in which companies share product’s information, such as demand, holding costs, among others, which is consolidated by the supplier, who is in charge of defining the joint replenishment plans for all customers. This collaborative approach is depicted in Fig. 1, where a dotted line indicates an information flow and a continuous line indicates a physical-material flow in the replenishment process.
The information required in the collaborative planning process is the products demands, inventory levels, ordering and storage costs in every customer. This information can be consolidated and managed by an actor of the distribution process or by an external entity, depending on the ability to make the distribution plans or for information security issues [1]. This entity, which in this article is the supplier, follows the Vendor managed strategy, defining the supply plans for all customers in the same time horizon through the application of the JRP. The JRP model is presented in equations 1 to 6, using the indirect grouping strategy (IGS). In this, the optimal common cycle time T* and the set of k i integer numbers correspondent to multiples of the cycle time are calculated. Products with the same value of k are ordered at the same time. For example, a product with k = 1 is ordered every cycle time, a product with k = 2 is ordered every 2-cycle times, and so on [39].
The order quantity for each product (Qi) in every cycle time is expressed in equation 1 and the total annual cost incurred for holding every product i can be calculated using equation 2. The ordering cost for each item is given by equation 3, which must be added to a fixed ordering cost S that is incurred every time a replenishment operation must be deployed with at least one product.
In those equations, i represents product index with 1 ≤ i ≤ n, where n is the number of products to be ordered. Di is the annual demand of product i, T is the order cycle time (time between orders) in years, h i is the holding inventory cost and Si is the variable cost of including the product i in an order. The total replenishment cost can be calculated with equation 4.
The optimal cycle time T* and the minimum total cost can be expressed in terms of the k i integers for the n products, as expressed in equation 5 and 6. Therefore, the problem is reduced to calculate the k i integer numbers as proposed by [47].
Due to its combinatorial nature, the JRP is considered a NP-Hard problem, making it necessary to use advanced solution techniques, such as specialized heuristic and metaheuristic tools. Genetic and evolutionary algorithms [48-50] are a useful metaheuristic for solving complex mathematical problems, which can be used to find solutions to the joint replenishment problem [36,46,48]. A genetic algorithm developed to solve the JRP model in the collaborative inventory planning approach is presented in the next section.
5. Genetic algorithm for the joint replenishment problem
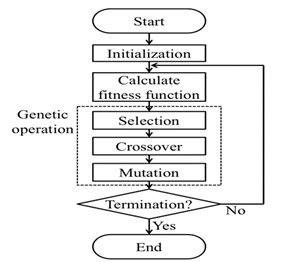
Genetic algorithms are advanced search techniques based on the evolutionary concept of natural selection, in which an individual represents a feasible solution to the problem and the more suitable individuals survive to future evolutions. In these algorithms, a population of individuals evolves by submitting each individual to operations of selection, crossing and mutation, from which new populations are obtained. It is expected that after a certain number of evolutions the optimal solution to the problem, or at least a closer one, will be found in a reasonable computation time [46,51]. Fig. 2 represents the evolution process of a genetic algorithm [46].
Genetic algorithms are good at solving complex computational problems [1,52,53] with characteristics of discontinuity, multimodality, noisy evaluation functions [54,55], non-linearity and non-convex solution spaces [56]. In the scientific literature it is possible to find several works that use genetic algorithms and other evolutionary computation techniques to solve the JRP, such as the works of [34,35,39,40,46-48,57-59,60,61].
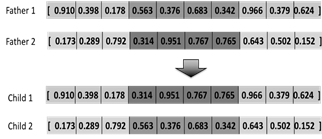
The individual is represented by the chromosome. In the case of the Joint Replenishment Problem, this representation can be done through a vector of integer numbers [35], real numbers [47] or binary numbers [34]. In this article, a real number representation is used following the work of [47], as depicted in Fig. 3 for a 10-product joint replenishment process. In the proposed individual representation, a gene located in the position i represents the k i value for the ith product. These real numbers are coded into the k i values by the procedure presented in [47]. Using real numbers coding facilitates determining the upper and lower limits for the k i values in order to make a more accurate search in the solution space, as proposed by [34] and [47].
The chromosome presented in Fig. 3 indicates that products 1, 2, 3, 7, 8 and 9 must be ordered every cycle time; products 4, 5 and 10 must be ordered every 2-cycle times; and product 6 must be ordered every 5-cycle times. The cycle time and total cost are calculated internally by the genetic algorithm using equations 5 and 6. Equation 6 corresponds to the algorithm fitness function.
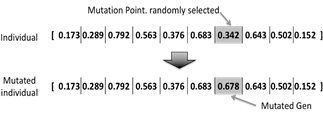
The crossover operation is done by using a two-point crossing method, as shown in Fig. 4. For this procedure the crossing points are selected randomly. The mutation operation is carried out using the one-point method as shown in Fig. 5. The mutation gene is randomly selected and its value is changed by a random number between the lowest and the highest real value of the entire chromosome that represents the k i .
The initial population is randomly generated and the selection for crossing is made using tournament, in which the individuals are randomly selected until completing groups with a capacity equivalent to the 10% of the population.
6. Methodology
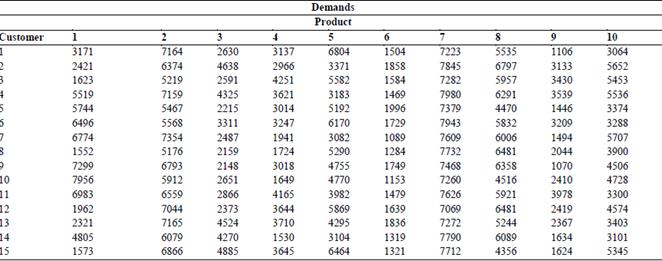
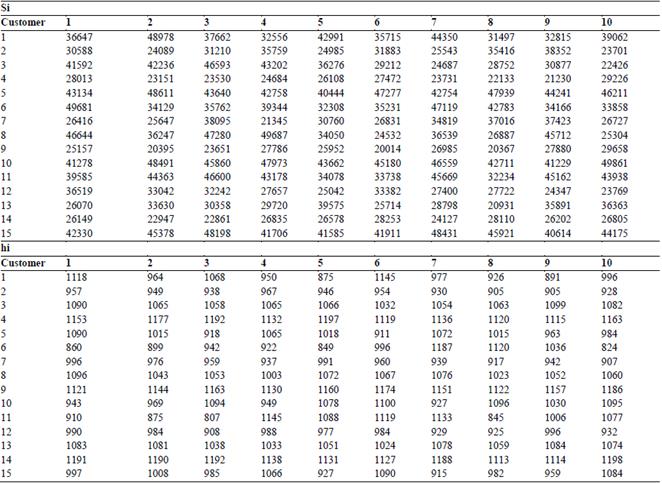
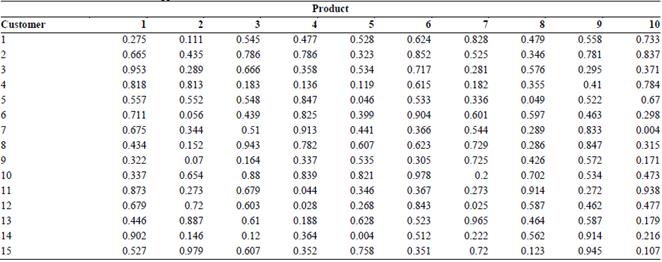
The collaboration approach presented in this article is applied in the collaborative distribution process of 15 organizations in the city of Medellin, Colombia. These companies are located in the midtown area and are part of the food industry. 10 different products that are supplied from the same provider were selected for the analysis. The demands of each product for the 15 customers are presented in Table 1. As mentioned above, the supplier is in charge of consolidating and managing the information under the VMI strategy [29]. Table 2 presents the holding and individual ordering cost for each product in every customer. The fixed ordering cost is equal to 150,000.
The replenishment plans for the 15 customers were made by two ways: first, using the collaborative approach and then using only the JRP model to calculate the individual replenishment for every customer (Individual Approach). In the first case, there is only one plan that corresponds to the 15 customers, but in the single calculation there is one plan for every customer. The comparison of the two ways allows determining the alternative that reduces the logistics costs for the total supply network.
In the collaborative approach, the replenishment plan for the products of all the customers is calculated using the genetic algorithm presented in the previous section. In this approach, a genetic representation was used that consolidates all the products for all the customers, so a vector with 150 genes was necessary, corresponding to the 10 products of each of the 15 customers. In this chromosome, the first 10 genes correspond to the first customer, the next 10 genes correspond to the second customers, and so on. In the individual approach, as there is a single plan for every customer, the chromosome representation corresponds to the individual depicted in Fig. 2 for 10 products to be jointly replenished. According to this, the genetic algorithm presented is used for both approaches and it only differs in the chromosome representation.
7. Results
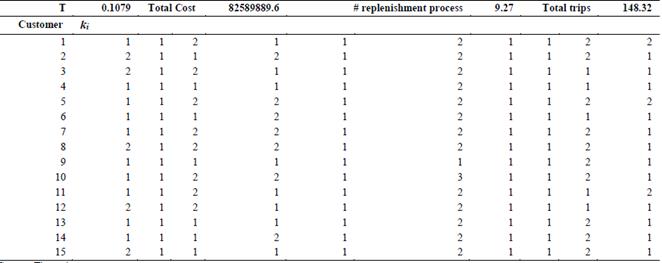
Table 3 presents the best individual obtained with the genetic algorithm for the collaborative approach, which produces the lowest replenishment costs. It must be noted that this individual is a vector of 150 genes, but for presentation purposes it is depicted as a table. This best individual for the collaborative approach can be easily decoded to the k i integer numbers corresponding to the multiples of the cycle time using the procedure established by [47]. Table 4 shows the results for the collaborative approach, in which k i values are expressed as integer numbers, as well as the cycle time, the total cost and the number of trips required for the replenishment plan.
In the individual approach a single replenishment plan is produced for every customer. In this case collaboration occurs only between a single customer and the supplier, and the inventory information of the other customers is not considered for determining the replenishment plans. In this sense the replenishment plan for every customer is also established by the supplier following the VMI.
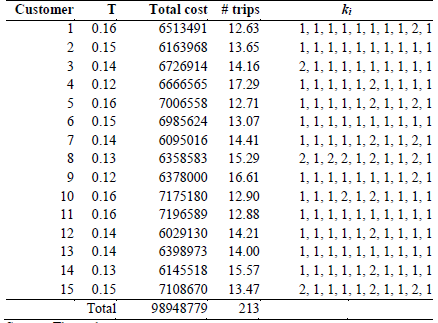
The distribution plans for every customer obtained with the individual approach are presented in Table 5. As expected, for every customer there is an assigned optimal cycle time T*, a total cost and a yearly number of trips. It must be considered that in each case the number of trips is multiplied by two, indicating at least one round trip between a single customer and the supplier. From this table it can be observed that the k i values for the products of customers 2, 6, 11 and 13 are equal to 1, indicating that all products must be jointly replenished every cycle time in order to reduce the logistics costs. For this individual approach, the highest k i value is 2 while in the collaborative approach it is 3, but only for one product. However, the k i assignment between the two approaches is very different, indicating significant changes in the distribution plans.
Table 6 shows the comparison for the collaborative and individual supply plans calculated using the genetic algorithm for the JRP model. From this table it is possible to observe that through collaboration the total costs and the number of trips are reduced. This is attractive for companies and city administrators since through the collaborative effort companies can lower their operating costs and also reduce a negative impact to the city, as the congestion caused by trucks circulating within the urban areas because the number of required trips is also reduced.
4. Conclusions
In this article a collaborative approach was presented to deal with the problem of jointly replenishing products from several companies, using the joint replenishment problem -JRP model. The single JRP model allows that multiple products in the same organization can be ordered together, reducing total costs. This model can be expanded for several organizations through a collaborative process in which the individual information is shared for the calculation of the joint replenishment processes. The application of this collaborative approach is done by grouping all the products in a single calculation, which is solved by using a genetic algorithm, due to the mathematical complexity that it implies.
From the comparison of the collaborative approach and the results obtained when determining the supply plans individually for every customer, it was observed that in the collaborative proposal, the replenishment plan produces lower costs and a reduced number of trips required for the replenishment process. These results make the collaboration approach attractive for companies and very relevant to the urban goods distribution processes, in the sense that it allows more economical replenishment operations for companies and reduces the number of vehicles circulating inside the cities, contributing positively to city congestion and to reducing greenhouses gas emissions.
As future research lines, the inclusion of capacity and resource restrictions in the JRP model is suggested, as well as considering joint replenishment problems with several suppliers. The integration of the joint replenishment problem with the Vehicle Routing Problem (VRP), looking for their simultaneous optimization, could be another interesting research line in urban goods distribution that will probably produce cost savings and the mitigation of negative impacts to society and the environment.