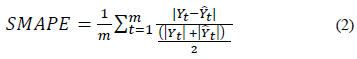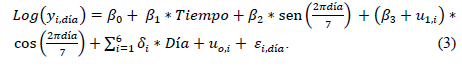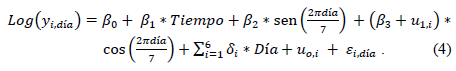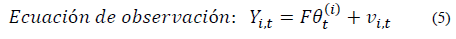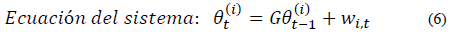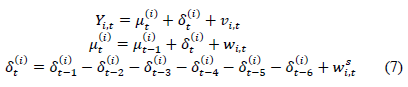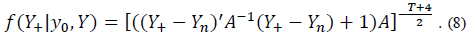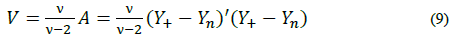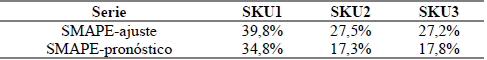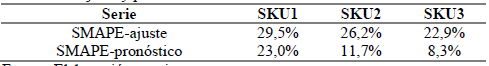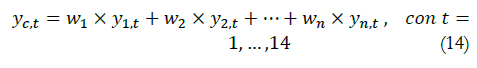1. Introducción
En la industria de alimentos, una adecuada predicción de la demanda es de gran ayuda para la gestión óptima del abastecimiento, especialmente en los productos procesados cárnicos, debido a su corta vida útil y la importancia de su calidad relacionada con la salud humana [1]. Es allí donde se buscan modelos estadísticos con precisión en los pronósticos de las ventas en este sector para contribuir a una planeación de producción e inventarios eficientes y con mínimos costos por desperdicio o mal servicio [2,3]. Algunos de los modelos de pronósticos con mayor aplicación han sido: Regresión, modelos ARIMA, modelos dinámicos lineales, y para estructuras multivariadas, entre otros. Para realizar dichas predicciones, los datos se toman de forma cronológica, siendo usual que presenten estructuras correlacionadas y características o patrones no siempre visibles como: tendencia, estacionalidad, ciclos, y aleatoriedad [4,5].
Todas las organizaciones operan en una atmósfera de alta incertidumbre, en especial aquellas con problemas tecnológicos [6,7], pero deben tomarse decisiones para planear. Para los administradores de una empresa, las inferencias a futuro basadas en información histórica y modelada con precisión, son más valiosas que las presunciones sin bases [8]. Lo anterior conduce a una necesidad de proveer modelos precisos y de fácil acceso para que los empresarios tomen buenas decisiones.
Hasta ahora se ha visto cómo desde la estadística clásica se han presentado modelos que permiten estimar el comportamiento de las variables de interés, desde otra perspectiva, se presenta la estadística bayesiana la cual ha tenido una alta popularidad en los últimos años para diferentes tipos de aplicaciones, como pronósticos. Estas técnicas de inferencia Bayesiana tienen en común una distribución de probabilidad a priori, de manera que se pueda hacer un reajuste de medidas iterativamente, combinándose con diferentes distribuciones de probabilidad de los datos. Éstas han sido usados en diversas aplicaciones de pronóstico como en [9]. En las últimas décadas, estas metodologías han tenido gran impacto en la modelación de problemas de pronóstico [11,12].
Por otro lado, los modelos lineales mixtos son estructuras multivariadas especiales que combinan componentes fijos con aleatorios, que también facilitan elaborar pronósticos con su forma clásica, o con estructura teórica Bayesiana [12], y para éste hay modelos clásicos basados en la distribución normal o en otras distribuciones como la Poisson y la binomial [13].
Sin embargo, también han surgido técnicas de combinación de pronósticos, que utilizan predicciones individuales de las series de tiempo [14,15] provenientes de diferentes modelos y la información de éstas, y se unen generando un sólo pronóstico. Recientemente también se han diseñado metodologías de combinación basadas en heurísticas o metaheurísticas [16]. Una heurística busca una solución muy aproximada a un problema, pero no necesariamente es la óptima, y una metaheurística es un proceso iterativo que guía y modifica las operaciones de otras heurísticas para producir eficientemente soluciones de alta calidad [17].
En este artículo se propone un modelo de combinación de pronósticos a partir de una metaheurística que se basa en los resultados de tres modelos: Modelo Lineal Mixto, Modelo de Regresión Bayesiana y Modelo Lineal Dinámico Bayesiano Multivariado, donde se usa el software R, que puede ser replicado en cualquier otro programa siguiendo el proceso descrito en detalle aquí. El criterio definido para evaluar el desempeño de los modelos será SMAPE. La metaheurística a utilizar es Colonia de Hormigas conocida en inglés como ACO (Ant Colony Optimization), y se minimiza la función objetivo de SMAPE.
El artículo se presenta de la siguiente forma: En la segunda sección se presenta una revisión de modelos estadísticos a utilizar y el proceso de la combinación de pronósticos. En tercera sección se expone las aplicaciones de los modelos y combinación a un caso de estudio, con un análisis exploratorio de los datos, así como los resultados de los modelos ajustados con la comparación de las medidas de ajuste y de precisión de pronóstico. Seguido a lo anterior, se muestran los resultados de la combinación de pronóstico mediante la metaheurístca ACO. Finalmente, se presentan las conclusiones, discusión y las referencias.
2. Revisión de literatura
Son numerosos los autores que usan metodologías clásicas para obtener pronósticos [18-20], en especial la industria. Los pronósticos de demanda son usados en modelos de inventario para generar una optimización posterior en su planeación por ejemplo, del control de inventarios [2,21]. Sin embargo, algunos modelos clásicos presentan problemas al ser estimados, es el caso de los modelos de regresión lineal y los modelos ARIMA [4,18], [19,22], que deberían cumplir con los supuestos teóricos de normalidad, varianza constante, incorrelación e independencia en los residuales [18-20], en adición Simchi-Levi et al sugiere que en algunos casos la estimación se afecta debido a cambios drásticos externos [20]. Un caso derivado de éstos modelos son los SARIMA o ARIMA estacionales, apropiados al existir patrones de éste tipo periódico
2.1. Otros modelos
Los modelos RNA (redes neuronales artificiales) son estrategias usadas entre otras cosas, para pronosticar y se basan en procesos de optimización. Se han utilizado para la predicción en casos en que la demanda también presenta variabilidad y estacionalidad como sucede en el sector cárnico [23]. Éstos modelos han sido usados a nivel internacional para realizar predicciones, por ejemplo, del precio de la energía [24], que se ha vuelto esencial en relación al suministro energético en muchas compañías a nivel mundial, usando en muchos casos, variables adicionales para su predicción, o algoritmos de optimización, incorporando parámetros, elementos o estrategias de búsquedas específicas, lo cual algunos han denominado Machine Learning, encontrando pronósticos que pueden ser más eficientes [25].
En las últimas décadas, la inferencia bayesiana ha tenido gran impacto en la modelación de problemas de pronóstico [10,11]. Los modelos lineales mixtos son especiales en estructuras multivariadas, como por ejemplo, incluir varios productos en la predicción de la demanda; este modelo se conoce y estima en R con la teoría clásica, pero también, puede estimarse en éste programa, su estructura teórica Bayesiana [26,27]. Para éste hay modelos lineales mixtos clásicos basados en la distribución normal o los generalizados, en otras distribuciones como la Poisson y la binomial [13].
En [10] presentan un modelo lineal un modelo lineal dinámico basado en la inferencia bayesiana (BDLM) para predecir el tiempo de viaje en línea a corto plazo en un tramo de autopista. [11] propone una nueva técnica de pronóstico para el consumo de energía con enfoque bayesiano llamada Bayesian Heating Oil Forecaster (BHOF). Se han usado los modelos dinámicos bayesianos, empleado también el filtro de Kalman en diferentes trabajos y composiciones para pronósticos multivariados y univariados en diferentes tipos de sectores industriales e investigativos. Modelo bayesiano lineal dinámico multivariado, como en [28] y otro tipo de modelos basados en estadística bayesiana en [29-31] en especial, [30] usan una técnica de combinación de pronósticos con base en teoría Bayesiana.
Finalmente una de las metodologías propuestas con resultados exitosos son los modelos de regresión bayesiana, algunos autores han realizado comparaciones de éstos y otros modelos para realizar pronósticos [32-34]. En [32] se propone una comparación para evaluar el desempeño de modelos clásicos y bayesianos frente a series de tiempo simuladas con variaciones estacionales y con efectos drásticos logrando el mejor resultado para una regresión bayesiana (BRM).
2.2. Combinación de pronósticos
Como lo mencionan [35], las ponderaciones de pronósticos iniciales fueron propuestas en el año 1969 por los autores Bates y Granger [36] asumiendo que las predicciones son insesgadas [37], pero además, en [35] proponen una combinación lineal de los pronósticos.
La combinación de pronósticos también puede realizarse usando técnicas bayesianas, dado que se puede obtener un mejor resultado al combinar la predicción desde diferentes modelos y fuentes de información. En [30] introducen un nuevo método de combinación basada en juicio de expertos con un modelo basado en densidad de pronósticos al cual se aplica inferencia y predicción bayesiana.
En [38] menciona que “Bajo el criterio de minimizar la varianza del error del predictor, la combinación de pronósticos individuales, ya sea con errores independientes o correlacionados, es óptima, y nunca peor, en teoría, al pronóstico del mejor modelo individual”. Además de esto, en [35] mencionan múltiples estrategias para realizar combinación de pronóstico, que además pueden tener mejor desempeño que otros modelos de regresión.
Una heurística busca una solución muy aproximada a un problema, pero no necesariamente es la óptima, y una metaheurística es un proceso iterativo que guía y modifica las operaciones de otras heurísticas para producir eficientemente soluciones de alta calidad [17]. Entre éstas metaheurísticas existen algunas conocidas como búsqueda tabú, enfriamiento simulado, algoritmos genéticos, colonia de hormigas, entre otras [39,40].
Para el logro de un mejor resultado en la estimación de pronósticos en general, es posible minimizar algún criterio de información inferido como el MAPE (Mean of Absolute Percentage Error), SMAPE (Symetrical Mean of Absolute Percentage Error), RMSE (Root of Mean Square Error) [41].
La optimización basada en colonias de hormigas aprovecha las habilidades del comportamiento de estos insectos para encontrar un mejor camino al objetivo que buscan alimentos dejando un rastro para las demás; de acuerdo con esto, si aleatoriamente una hormiga elige un camino y es de los más cortos dejará un rastro de feromona mientras va desde la colonia hasta la fuente de alimento, su retorno a la colonia será más rápido y dejará nuevamente rastro de la sustancia, los caminos cortos tienen mayor probabilidad de que las hormigas los escojan [42]. Se debe tener en cuenta que la secuencia para encontrar la solución se realiza de forma discreta, o por pasos. Algunos ejemplos de aplicación de dichas técnicas son presentados por [43] donde resuelve mediante un híbrido entre colonia de hormigas (ACO), colonia de abejas artificiales (ABC) y búsqueda armónica (HS) para resolver el problema de despacho económico en un sistema de múltiples generadores.
3. Metodología
Los datos usados son de una empresa de cárnicos de la ciudad de Medellín, consisten en series de tiempo de ventas de 3 productos con 585 observaciones, en el periodo desde el 1 de enero de 2015 y finalizando el 7 de agosto del 2016.
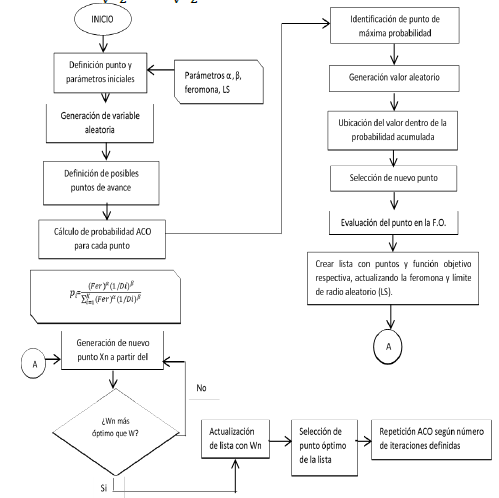
La investigación de éste trabajo es cuantitativa con alcances de modelamiento basados en correlación. La metaheurística se diseña en el programa R, estableciendo los pasos detallados que ésta requiere para que pueda replicarse en cualquier otro programa, pero para su uso se requieren otros pasos previos. En primer lugar, se parte de una exploración de datos para identificar patrones correlacionales y estacionales en las series de tiempo. En segundo lugar, se ajustan los modelos estadísticos a las series de tiempo, partiendo la base de datos en dos, la primera muestra se elige de 1 a n (n<N), usada en el primer ajuste y poder pronosticar los datos restantes con las ecuaciones encontradas, así se estiman el indicador SMAPE de ajuste (con n valores) [44] y de pronóstico de los datos restantes m valores (siendo m=N-n). Con éstos m datos se compara la capacidad de pronóstico de estos modelos entre los que se usaron de manera individual. En tercer lugar, se estima la combinación de pronósticos propuesta con los resultados encontrados de los modelos previos y se optimiza con el criterio SMAPE (pasos en el proceso de la Fig. 1), que se compara con los demás modelos. El SMAPE se presenta en la ecuación (2).
Donde Yt: Denota el valor real de la serie en el tiempo t.
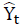 : Denota el valor estimado por el modelo para el tiempo t sea de ajuste o pronóstico.
: Denota el valor estimado por el modelo para el tiempo t sea de ajuste o pronóstico.
A continuación, se muestran los modelos de pronósticos usados a nivel individual y la combinación de pronósticos propuesta.
3.1. Modelo lineal mixto
El Modelo Lineal Mixto (MLM) tiene como ventajas las estructuras multivariadas en los datos que contemplan correlaciones intra y entre sujetos, en especial, para datos longitudinales, o con medidas en el tiempo que pueden ser afectados por dicha temporalidad, incorporando, además, otras covariables en la matriz de diseño como posibles fuentes de variación que afectan la respuesta. Por ello, el modelo se basa tanto en la matriz de diseño de covariables, como en el vector de la variable respuesta con todos los sujetos. Dentro de las posibles desventajas se encuentra que la predicción exige una combinación de coeficientes fijos con el componente estimado por sujeto dentro de la ecuación de estimación, pero que es fijo y no dinámico, con programación no automática. Otra limitación es que los residuales son muy sensibles a la lejanía de una distribución normal y la heterocedasticidad en la varianza, generando una violación de supuestos y errores en las estimaciones y pronósticos [13].
El MLM se presenta a continuación en la ecuación (3).
Donde: 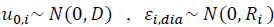 , con simetría compuesta en la correlación.
, con simetría compuesta en la correlación.
En la estructura de estimación, la matriz de varianza covarianza asociada a los residuales, asume que los valores observados para el i-ésimo individuo tienen una covarianza constante y varianza constante.
3.2. Modelo lineal mixto Bayesiano basado en la normal para los datos
El modelo se presenta a continuación en la ecuación (4).
En el proceso de estimación, la función blmer del paquete blme de R [45] puede utilizar una de las siguientes distribuciones a priori para los parámetros y matrices de varianza. Para los parámetros fijos se puede usar la distribución Normal, o la t o una no informativa. La distribución de probabilidad a priori para la matriz de varianza covarianza del (los) efecto (s) aleatorio (s) puede ser la Wishart, Invwishart, Gamma, Invgamma, o no informativa.
En el caso de la varianza de los residuales, su matriz de varianza puede tener una distribución a priori Gamma, Gamma Inversa, o no informativa. En este trabajo se prueban diversas combinaciones de distribuciones a priori hasta encontrar las que tienen mejor desempeño, definiendo una Wishart para la matriz de covarianza de los efectos aleatorios y la Normal para los parámetros fijos y no informativos para la varianza de residuales.
3.3. Modelo lineal dinámico Bayesiano
Este modelo contempla estructuras multivariadas, pero tiene una ventaja importante en la estimación, que permite actualizar los parámetros a medida que transcurren los períodos, ya que los nuevos datos se incorporan en la matriz de estimación a medida que se realiza el pronóstico, agregando además, un componente aleatorio en el error y la estacionalidad que se incorpora en las matrices de las ecuaciones del sistema espacio-temporal.
La ecuación general para la estructura del BDLM presentado en [46] para múltiples series se describe a continuación en las ecuaciones (5) y (6):
Donde: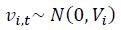 y
y 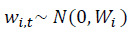 , son componentes de errores.
, son componentes de errores.
Yi,t: Es el valor de pronóstico que actualiza la media de la distribución predictiva en cada ciclo del filtro de Kalman.
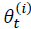 : Representa el vector de parámetros del sistema que también actualiza las distribuciones a priori y a posteriori en cada ciclo.
: Representa el vector de parámetros del sistema que también actualiza las distribuciones a priori y a posteriori en cada ciclo.
Para agregar la estacionalidad en el modelo, previamente se identifica el orden al cual corresponde. Para ésta investigación, luego del análisis exploratorio de las series de tiempo, se identificó que el orden estacional es 7, es decir, el patrón estacional es semanal, dicho comportamiento se debe agregar en el modelo y el diseño BDLM del autor Petris lo permite, luego de programar la cantidad y las variables específicas. La ecuación (7) expresa la forma en que el modelo incorpora dicho patrón al sistema al detallar los factores estacionales 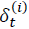 , que son los días de la semana, modelo que es adaptado y estimado en R con el paquete dlm [47], usado en este trabajo.
, que son los días de la semana, modelo que es adaptado y estimado en R con el paquete dlm [47], usado en este trabajo.
Donde los componentes de error siguen distribuciones normales multivariadas, donde, 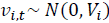
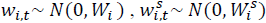 . Las funciones usadas para el pronóstico dentro del paquete dlm son dlmFilter y dlm.
. Las funciones usadas para el pronóstico dentro del paquete dlm son dlmFilter y dlm.
3.4. Modelo de regresión Bayesiana (BRM)
El modelo de Regresión Bayesiana se deriva luego de asignar una distribución normal a priori para el vector de parámetros (, de una ecuación de regresión y una distribución normal para los datos. Se utiliza una modificación del vector inicial de parámetros de regresión β0, pero el parámetro de precisión (0 = 1/σ es fijo. La deducción de la distribución predictiva usada para pronosticar es presentada en dicha tesis, la cual resulta en una T de Student.
La distribución predictiva, luego de hecha la integral del producto entre la posterior y la distribución futura de los valores a predecir, cuya demostración se presenta en [32], es (8):
Dicha función es una distribución T-student, con media, 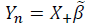 ( grados de libertad, y varianza dada por (9):
( grados de libertad, y varianza dada por (9):
Si bien el modelo BRM permite adicionar componentes diferentes a la misma serie de tiempo, pronostica con base en una distribución probabilística, que es la T de Student, también, facilita la estructura de actualización dinámica para los parámetros y el mismo pronóstico como variable aleatoria. A pesar de que su diseño no contempla una estimación multivariada, sino, univariada, ha mostrado ser más eficiente en el pronóstico de algunas series de tiempo, como lo muestra [32].
3.5. Procedimiento algoritmo ACO
Luego de estimar los modelos propuestos y hallar los respectivos pronósticos y sus medidas de precisión de ajuste y pronóstico, se seleccionan aquellos modelos que serán evaluados en la combinación de pronóstico usando la metaheurística ACO, este procedimiento se presenta a continuación en la Fig. 1.
4. Resultados
4.1. Estudio de caso
Se analizan las series de tiempo diarias de tres productos de una empresa del sector cárnico en la ciudad de Medellín, que se denotarán SKU1, SKU2, SKU3, para un periodo de un año y 8 meses aproximadamente, empezando desde el 1 de enero de 2015 y finalizando el 7 de agosto del 2016; las unidades corresponden al peso del producto vendido, con naturaleza continua. Del total de N=585 observaciones, se usa n=571 datos, haciendo el corte para el pronóstico con las últimas 14 observaciones (2 semanas calendario).
Parte 1. Análisis exploratorio
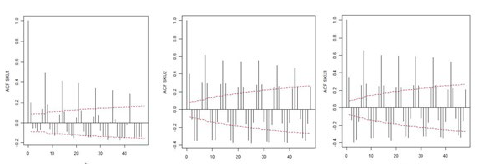
Las series de tiempo no tienen tendencias, pero al analizar el patrón de autocorrelación usando las funciones ACF, se aprecia estacionalidad para cada uno de los productos, con un patrón de orden 7 (Fig. 2), debido a los altos valores que se salen de las bandas en el periodo 1 y el patrón que se repite cada 7 periodos.
Esto indica la presencia de correlación de orden 1 y estacional 7, la serie no es estacionaria, y debe modelarse mediante una estrategia que involucre variables estacionales ya sean indicadoras o funciones periódicas.
Parte 2. Estimación de modelos
Posterior al análisis descriptivo y exploratorio se estiman los modelos propuestos en la sección métodos, buscando compararse en ajuste y pronóstico, este último usando también gráficos para una mejor interpretación.
Modelo lineal mixto clásico (MLM)
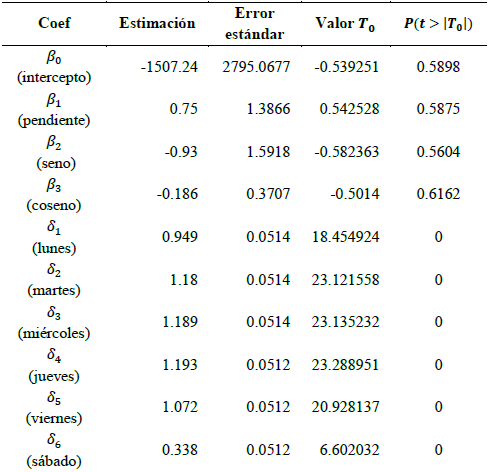
Los parámetros estimados para este modelo se encuentran en la Tabla 1.
Sin embargo, al no apreciar significancia de las primeras variables (hasta coseno), ya que la última columna muestra un valor P o de probabilidad de error mayor que el 5%, se reajusta otro modelo y se validan los supuestos de los residuales con la prueba de normalidad de Jarque Bera, intentando otros modelos lineales mixtos sin lograr mejor precisión del SMAPE.
Con esta estimación se obtienen los SMAPE de ajuste, con los 571 datos y al dejar los 14 restantes se calcularon los pronósticos del modelo para los 3 productos encontrando el SMAPE de pronóstico para cada modelo. Los resultados se presentan en la Tabla 2.
De acuerdo con los resultados se observa que para los productos SKU2 y SKU3 las medidas son inferiores al resultado del SKU1, que tiene un error muy grande en cuánto al SMAPE en pronóstico. Sin embargo, debido a la falta de precisión y significancia adecuadas, se descarta el MLM de la combinación de pronóstico, ya que puede introducir errores al pronosticar.
Modelo lineal mixto bayesiano (BLMM)
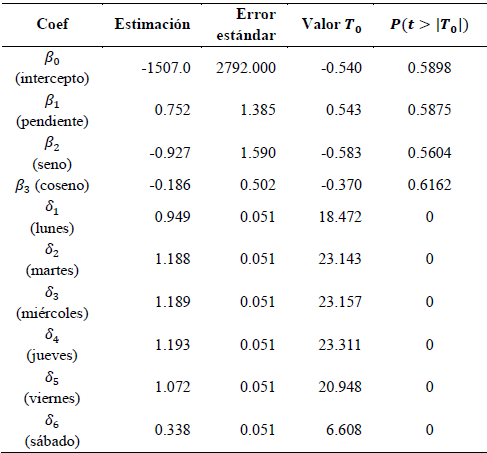
Los parámetros de este modelo se presentan en la Tabla 3.
Con los valores estimados y pronosticados comparados con los valores reales se obtienen las medidas de información presentados en la Tabla 4, de ellos se observa que, en comparación con el modelo anterior MLM, esta mejora levemente en cada una de las medidas de cada producto, sin embargo, no parece ser suficientemente significativo. El resultado es muy similar al del modelo anterior.
Modelo lineal dinámico (BDLM)
Los parámetros son dinámicos, y con ello se construyen tanto los valores ajustados como pronosticados para compararlo con los valores reales y calcular las siguientes medidas, que se presentan en la Tabla 5.
Este modelo mejora tanto en las medidas de ajuste, como de pronóstico.
Modelo de regresión Bayesiana (BRM)
Con la estimación del modelo con el nuevo proceso presentado en las ecuaciones (10), (11), (12) y (13), los resultados SMAPE presentados en la Tabla 6.
Se evidencia con estos resultados que el modelo BRM es candidato a ser el mejor en cuanto ajuste y pronóstico debido las buenas medidas que obtiene, en especial con el producto SKU3, que, con respecto a los modelos anteriores mejora entre un 30 y 50% de las medidas comparadas.
En la Tabla 7 se presenta el resumen comparativo de los modelos propuestos en cuanto a pronóstico para 14 días pronosticados.
Tabla 7 Comparación de medidas de pronóstico de los modelos individuales.
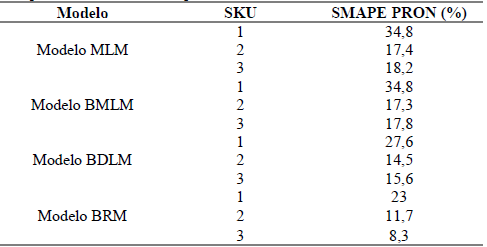
Fuente: Elaboración propia
Evidentemente se observa que el modelo BRM obtiene mejores medidas de SMAPE para cada uno de los productos, seguido del modelo BDLM sin embargo existe cierta ventaja del modelo BRM que se ve reflejada principalmente en el producto SKU3 y en tercer lugar está el modelo BMLM que tiene leves mejoras con respecto al MLM, similar al encontrado en [32].
No obstante, la propuesta de este trabajo consiste en combinar los modelos previamente usados en uno, donde se utiliza la metaheurística ACO para optimizar la medida SMAPE, como se presenta a continuación.
4.2. Combinación de pronósticos
De acuerdo con la estimación de los pronósticos de cada modelo, se plantea una estrategia de combinación de pronósticos mediante la metaheurística ACO presentada anteriormente con el objetivo de minimizar el SMAPE y encontrar los valores de los pesos óptimos de cada pronóstico, como se presenta en la ecuación siguiente.
Donde y c,t es el pronóstico ponderado usado para calcular el SMAPE.
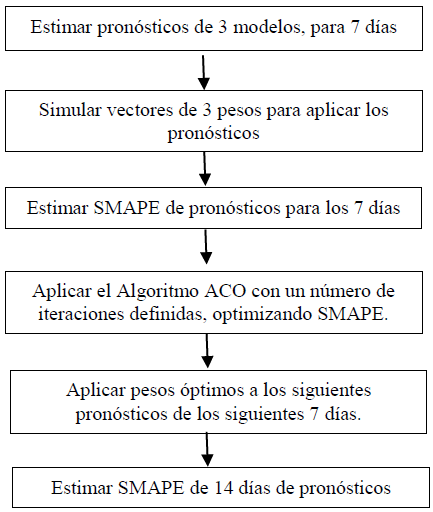
La validación de este algoritmo se realizará mediante una estrategia de optimizar con los primeros 7 pronósticos obteniendo los pesos óptimos, los cuales serán insumo para calcular los 7 pronósticos ponderados restantes y finalmente observar qué tan eficiente es este algoritmo en los 14 días. Se seleccionan los 3 mejores modelos en este caso son BDLM, BMLM, y BRM. El MLM se descartó dado que no se encuentra un modelo de éste tipo mixto con mejor precisión que el presentado en los resultados.
El resumen del proceso se muestra en la Fig. 3.
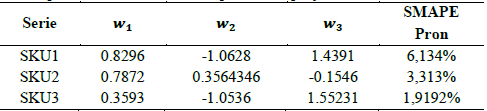
Los resultados de la combinación para cada SKU se presentan en la Tabla 8, donde w1 es el peso asociado al pronóstico del modelo BDLM; w2, el del modelo BMLM y w3 del modelo BRM.
El algoritmo se simuló repetidamente, y se encontró convergencia en los resultados. Los resultados de éste proceso de optimizar con 7 y proyectarlos a los demás 7 se muestran en la Tabla 8, donde el SMAPE es estimado para los 14 pronósticos en total. De esto se observa que el SMAPE es bastante bueno, con valores mucho mejores a los resultados de los pronósticos individuales de los 14 registros por cada producto.
4. Conclusiones
De acuerdo con los resultados, se evidencia que el modelo BRM logra ajustar y predecir de forma adecuada el comportamiento de cada uno de los productos del caso de estudio sobre el sector cárnico, obteniendo mejores medidas en pronóstico de acuerdo con SMAPE, esto conlleva a que el proceso de estimación mejora fuertemente en comparación entre los otros modelos propuestos para este tipo de series, sin embargo, la propuesta del algoritmo ACO para la combinación resulta ser mejor.
Según las investigaciones revisadas en diversos artículos como [35,37,38] etc. Las metodologías de combinación de pronóstico en la mayoría de los casos proveen una mejor solución y alternativa versus un único pronóstico puntual, aspectos que también se encontraron en éste artículo. En este artículo se observó cómo mediante una combinación de pronósticos usando la metaheurística ACO aplicado al caso de estudio, usando un radio variable de búsqueda se encontró un camino eficiente, obteniendo mejores resultados en la medida de SMAPE que el mejor modelo individual de pronósticos usado, el BRM, tanto así que logró reducir de un el SMAPE de 22% para el SKU1 a un 6% aproximadamente, lo que es un 74%. Para los SKU2 y SKU3 se presentaron reducciones del 74% y 77% respectivamente, es decir se obtienen eficiencias bastante altas.
Se proporciona una técnica innovadora para que otros investigadores o académicos puedan efectuar pronósticos basados en una búsqueda que usa un algoritmo diseñado en el programa R, donde no deben preocuparse en elegir un solo modelo, sino que pueden usar varios de ellos para mejorar la precisión de los pronósticos.