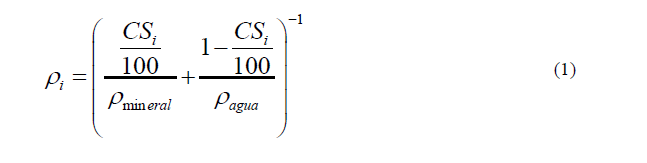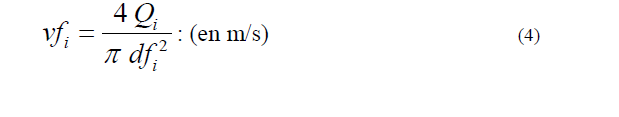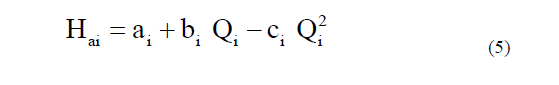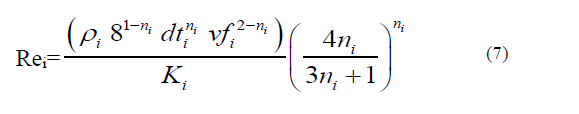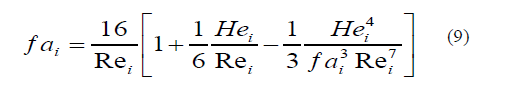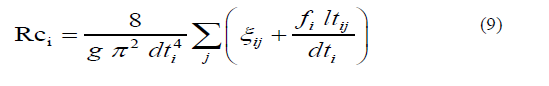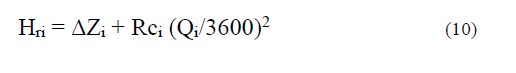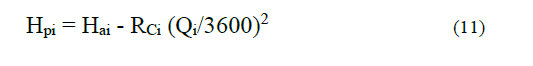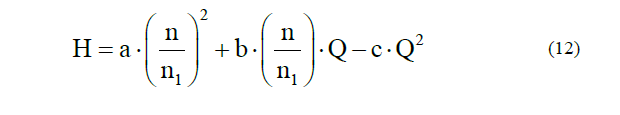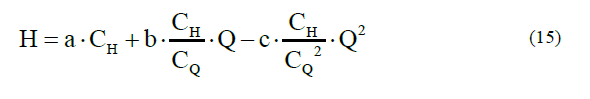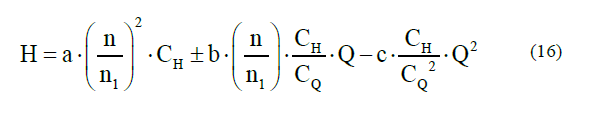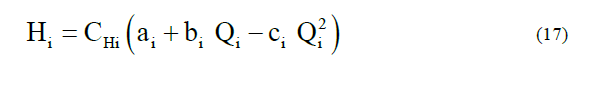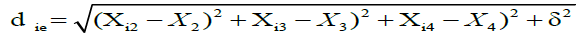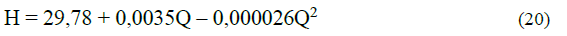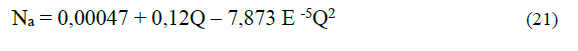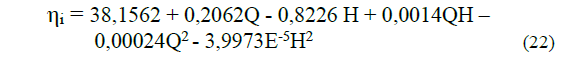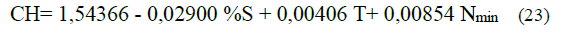1. Introduction
In the industries that process the Cuban laterite ore, the fluid transport systems are consumers of an important part of the energy used for productive purposes. More than 60% of the total energy consumed in the transportation of fluids occurs through electric drives with induction motors and, of this consumption, more than 55% is used in pump drives [1-4]. For this purpose, sufficient information must be available about the behavior of the rheological parameters of the hydromixes as a function of the concentration of solids, the temperature and the granulometric composition in the range of variation of these factors in the operating conditions of the transport system.
Several research have been carried out with the purpose of operating pumping systems and for the estimation of pressure losses in pipes [5-8] from which valuable experimental results have been obtained from the testing of pumping equipment already built by firms of recognized international prestige; The main limitation of most of these results is that they were obtained with water as fluid in the tests. Studies have been published that abaut the modeling of centrifugal pumps [9-11], which are mainly devoted to the study of the transport of sugary honeys from the sugar industry, where correction factors of the characteristic curves are obtained [12, 13]. The mathematical models that allow the estimation of load and design capacity as a function of the exit blade angle, the specific velocity and the viscosity of the fluid other than water have also been developed [14]. The flow rates of the pumps used depend considerably on the rheological characteristics of the fluid transferred; however, due to the insufficient available knowledge of these characteristics, the selection and exploitation of them is done when considering that the rheological behavior of the fluids is Newtonian [15-17].
As stated by Turiño [9] there is no theory that allows to predict the exact behavior of a pump when handling a viscous fluid. The simplest method to determine the operating parameters (load, flow, power and efficiency) and reconstruction of the characteristics when varying the viscosity is based on the use of correction coefficients, specific for each fluid, obtained experimentally. Experimental research developed by [12] in relation to the pumping of sugar solutions of a non-Newtonian nature, proposed correction coefficients that allow to predict the characteristic curve of these pumping equipment based on the rheological properties of the tested fluids.
Several authors [18-21] provide a simple model H= a + b.Q - cQ2 to describe the operational load-capacity characteristic of radially designed centrifugal pumps. The constants a, b and c of this model must be obtained from an adjustment of the characteristic curves provided by the manufacturer of these equipment. Generally this information, published in commercial catalogs [22] is for clean water under conditions of normal pressure and temperature, as well as for a constant outside diameter and speed. Therefore, this model does not take into account the operation at other speeds of rotation and outside diameter of the impeller or the application of these equipment in the pumping of viscous fluids.
By having the correction coefficients of the load and the capacity of the centrifugal pumps for various Newtonian and non-Newtonian fluids, according to the sources of information analyzed, it is possible to correct the operational characteristic, however, the correction coefficients reported are for oil, pulps of food, paper pulps, chemical pulps and sugar solutions, which does not allow to obtain what are the correction coefficients of lateritic pulps at different concentrations. Therefore, the objective of this paper is to determine the coefficient of correction of the behavior of the characteristics of the load curves of centrifugal pumps, by using mathematical models that take into account the rheological properties of the lateritic pulps.
2. Procedure and experimental technique
In the case of lateritic pulps several factors have a direct effect on the rheological behavior and their levels are essential to improve their viscosity. Among the factors involved in the process of transporting hydromixes from the acid leaching process, the effects of total solids concentration, particle size distribution, pH, and mineralogical composition can be analyzed and as main factor the temperature of the suspension. Once determined the factors that can influence the rheological parameters requires laboratory work and mathematical processing of the experimental values obtained as well as a large volume of historical data of the process of thickening and pre-heating of pulps that allow the characterization of the main mineral suspensions that are manipulated in this stage of the productive process.
2.1. Experimental design
The rheological properties or dependent variables that are of special interest to adequately design the efficient operation of the pumping system are: μa: apparent viscosity of the suspension (Pa·s), (0: Initial shear stress (Pa), K: index of consistency (Pa·s n) y n: index of consistency.
The independent variables characterized by the factors that define the rheological characteristics of the lateritic hydromezclas. s: characteristic parameter of the granulometry (Coefficient of Polidispersión). %S: characteristic parameter of the granulometry (Coefficient of Polidispersión). Nrmin: Mineral number (chemical composition) and T: temperature (°C).
Due to the complexity to control the Polydispersity Coefficient and Mineral Number variables, a 5x7 Full Factorial Experiment was designed for the variables or factors concentration of solids and temperature. To guarantee sufficient representativeness of the Polydispersity Coefficient and Mineral Number variables, composite samples were selected in the two points of the study object. In summary, the sample has 140 physical samples and is characterized by: Two Compound Samples to guarantee the representativeness of the other two independent variables and three repetitions for each case that ensure the accuracy of the results.
2.2. Description of the sampling
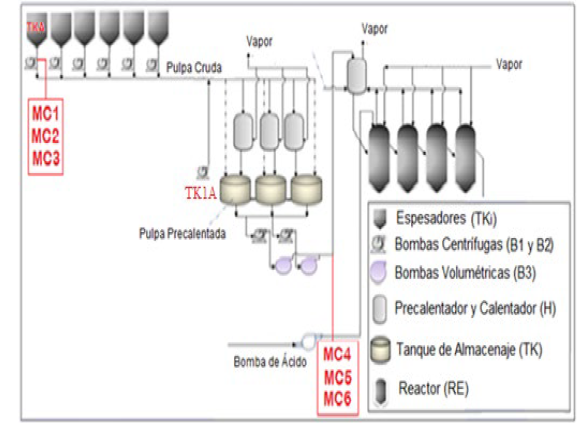
Two Productive Demonstration Units (UDP) were selected) [23] see Fig. 1 and for the experimental analysis of the lateritic pulp, two sampling points were taken: Point No. 1, lateritic pulp at room temperature extracted from the bottom of the conventional thickener (TK-1A) where the sedimentation process occurs, where a solid content in the thickener cone between 46 and 48% must be achieved, by design. Point No.2, lateritic pulp with a temperature of more than 90 oC, this temperature was reached in the preheater by direct contact with steam of 103.42 kPa countercurrent. The sample is taken in the discharge of the volumetric pumps.
Samples were collected at the selected points of 500 ml of pulp in a volumetric of 1000 ml to prepare 6 composites. A total of five 200 g samples were prepared with three replicates for the concentrations of solids selected from the Composite Samples by UDP, contained in 250 ml stoppered vials. In four 1000 L pulp tanks and one 1,000 L deposit of overflow water from sampling point 1, the sample was taken for the experimentation of the correction coefficient. For the dilution of the initial pulp, water was added and to obtain concentrations higher than 40% solids, the pulp was allowed to settle and water was extracted by decantation. The chemical samples, granulometric analysis and the number of mineral, chemical and granulometric composition were determined for the composite samples.
It was decided to evaluate and take as references the historical data of each variable. Five ranges of polydispersity coefficient: 0.1 to 0.3; 0.31 to 0.5; 0.51 to 0.7; 0.71 to 0.9; 0.91 to 1. Five values of solids concentration: 37, 40, 43, 46 and 48 %. Seven temperature values: 28, 40, 50, 60, 70, 80 and 90 °C. Three ore number intervals: 0 to 6.9; 7 to 14; 14,1 to 20, the values of the independent variables are classified in intervals that guarantees the representativeness.
2.3. Experimental collection of the operational parameters of centrifugal pumps
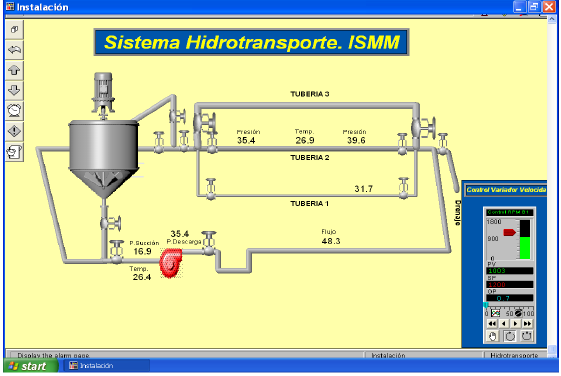
The research of the parameters and transportation regimes was carried out in the hydrotransport experimental station of the Higher Metallurgical Mining Institute of Moa. It consists of equipment and accessories that allow higher quality in the registration and control of variables and their subsequent processing, through the CitectSCADA data acquisition program, see Fig. 2.
2.4. Methodology for the collection of experimental data
The fundamental characteristic of the operational diagnosis of pumping systems is to obtain the system's energy parameters (flows, loads, hydraulic losses, power and efficiency) at the point of operation, which requires a series of data.
Calculation procedure to adjust the characteristic curves of the pump for water, when pumping lateritic hydromixes. Adjustment of the characteristic curves of the pump for the pumping of water and the lateritic hydromixes.
a) They are determined from the characteristic curves of the pump (for water) for 60%; 80 %; and 120 % of Q design, Load values; Efficiency and Power.
b) Multiply the correction coefficients determined by the load values; expenditure; efficiency and power for water for 60%; 80%; and 120 % of the Q design.
Qpulpa = CQ Qwater; Hpul = CH Hwater; ηpulp=Cη ηwater; Ppulp = ρpulp * Qpulp * Hpulp / ηpulp, (watt); yes: ρ pulp (N/m3); Qpulpa (m3/ h); Hpulpa (m).
The number of experimental runs was determined from the application of a multifactorial design. In correspondence with the determined levels of each variable, at least eight levels of the volumetric flow are established for values of solids content in the lateritic hydromix of 37, 40, 43, 46 and 48 %, for the pipe diameters of 150 mm, three repeticions of the experiments. The processing of the data is carried out by the admissible errors of the values of the variables. For this test, parameters were measured such as pressure drop (Pa) in the pipe, load, speed (m/s), flow rate (m3/s), power, (kW), efficiency and determine the experimental correction coefficient with the objective of obtaining the point of maximum efficiency with the variations of the concentration of the hydromixes.
2.5. Equipment and materials
The equipment used to perform the experiments were the following: To determine the physical characteristics of the selected samples: X-ray fluorescence spectrometer, analyzer of particle size of the "Analysette 22" COMPACT type, Ohaus drying scale.
To determine rheological properties: HAAKE VT 550 viscometer, Mettler Toledo digital technical scale, Ohaus drying scale, IKA RW 28 mechanical impeller, Cimarec thermal plate, Master Flex Model 77601-10 water pump. The experimental installation of hydrotransportation has the following instruments: pressure sensors (SITRANSP) from 4 to 20 mA, PT-100 thermoresistance (SA TERMIBEL N.V), KROHNE Electromagnetic flowmeter, model OPTIFLUX 2100/4100, DT 301 density meter (DensityTransmitter), PQM II GE Multilin network analyzer.
In addition, the utensils were used: 500 ml test tubes, 500 ml beakers, 20 L container, 20 ml syringes, 250 ml bottles and 1000 L container.
2.6. Procedure for the correction of the load characteristic of centrifugal pumps of lateritic
The pumping of the flows from the suction tanks TKA, TKB, TKC, TKD, TKE, TKF to the discharge tanks TK1A, TK2B and TK2C, must guarantee the productivity of the Leaching Plant which are the essential requirements to stabilize the flow requested (FT) and solids concentration (PTo %). It must also be efficient when considering energy criteria of the required pumping power.
For each tank TKi (i=A, B, C, D, E y F) the following data are known: Vai: Current volume, m3; Vui: Useful current volume, m3. CSi: Concentration of solids in the current useful volume, %; Ti: Temperature, °C; Nrmin: Mineral number, dimensionless; si: polydispersity coefficient, dimensionless.
The parameters from the obtained rheological model were stablished. In addition, densities are calculated ρi [24] through the expression 1:
For each centrifugal pump B1i the following data are known: nrei: Standard speed, r/min; nrmi: Maximum speed, r/min; Characteristic equation for height:
Characteristic equation for the power:
Nomogram of efficiency values R as a function of the values de Q y H.
For each section j of each hydraulic network i is known: Diameter of the pipeline: dtij (en m); Length of the pipe: ltij (en m); Coefficient of resistance of the accessories [25]: ξij (dimentionless); Height Hdischarge_i y Hsuction_i of the hydraulic networki: (en m)
If it is considered that all this analysis is done for one hour of work, the volume (given in m3) can be substituted by the flow given in m3/h. Then, we have that the flows Q1, ..., Q6 are numerically equal to their corresponding volumes V1, ..., V6.
Knowing the limit velocity of the deposit and sedimentation, the fluid velocities are calculated vfi [26, 27] for each hydraulic network i by expressing:
Calculation of the load heights required by the network for each deposit:
a. Calculate the heights:
b. Calculate the Reynold number [27-29] by the expression:
For plastic fluids
For pseudoplastic fluids
c. Calculate the Hedstrom number [29] using the expression:
d. Calculate the number of Fanning fai [25, 29, 30] using the algorithm:
If He1<10 then fai = 16/Rei, otherwise solve the equation:
The graphic method based on nomograms can also be used [29, 30].
e. Calculate Darcy's number as:
f. Calculate coefficient of mechanical resistance through which the RCi luid is transported by means of the expression:
g, is the acceleration of gravity, m/s2
g. Calculate ΔZi as the difference between the discharge height minus the suction height.
h. Calculate the height of the network (value to be reached when pumping the pulp)
i. Calculate the Hpi height that would be obtained if pumping pulp at the nrei speed:
Calculation of the new equation of the characteristic curves of each pump.
The correction coefficient CHi is calculated by the mathematical model obtained from the ratio of the height of the water and the pulp at room temperature and CQi=1 is taken for each pump by replacing the laws of similarity [14] in the model of the pump characteristic, we obtain the relation [9] that describes the model for a new speed n.
nr: new desired speed of rotation, r/min; nr1: speed of rotation for which operational characteristics are known, r/min
When obtaining the load and capacity correction coefficients of the centrifugal pumps for viscous fluids, it is possible to correct the operational characteristic of these equipment by means of the following known relations:
HExp: Experimental load with viscous fluid, m; Hwater: load with water, m; Qexp: Experimental flow with viscous fluid, m3/s; Qagua: flow with water, m3/s
When only the fluid type is changed the expression 14 It transforms in:
After integrating expressions 14 and 17 you get:
By having the correction coefficients of the load and the capacity of the centrifugal pumps for various Newtonian and non-Newtonian fluids By means of equation 19 the new equations of each pump are obtained for the calculation of H as a function of Q, valid respectively for the speeds nrei:
Calculation of spin speeds nrdi
Using the equation of similarity, the following are calculated:
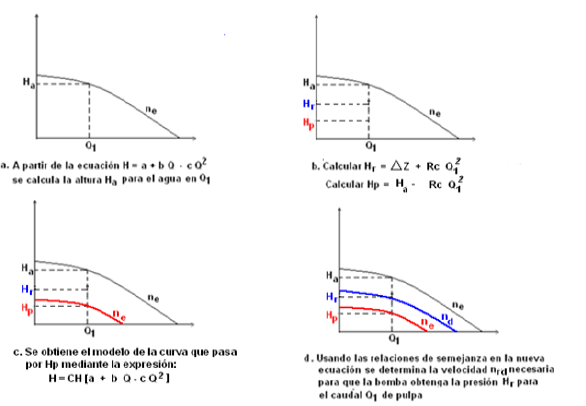
The methodological principle that is the basis of this step is illustrated in Fig. 3, which shows the decrease in the height of load when pumping water and a viscous fluid, knowing the correction coefficient and the similarity ratios it is possible to determine the speed of necessary rotation to pump at a desired height and flow.
Calculation of efficiencies of the ηi pump
Efficiency values are estimated using the Least Squares model obtained from the nomogram of the pump supplied by the manufacturer.
Calculation of pumping power
By the expression:
the power values in kW that are valid for the speeds are calculated nrdi.
3. Results and discussion
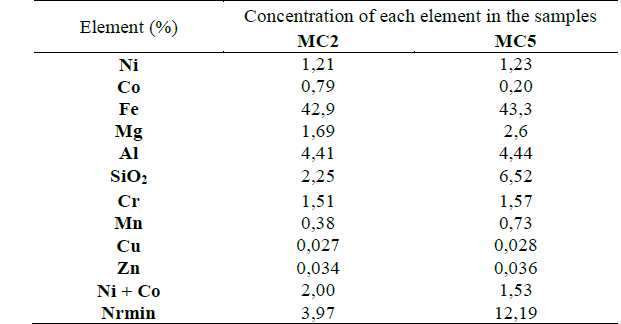
Compounds of mineral raw material that enter the acid leaching process have Fe content in the order of 45%, including other components such as Al of 4,5 %, Mg (from 1,69 to 2,6 %) the presence of light metal minerals provide a low density; its presence in the pulp is an unfavorable factor for sedimentation [31, 32]. are shown in [Table 1 ]
The granulometric distributions are constituted by small particles, less tan 50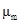 , they are the ones that gives plastic properties to the pulps. There is a predominance of fine fractions of general form and D80 corresponds to that of particles smaller than 7 µm, which indicates that 80% of the sample has a diameter smaller than this value, therefore, most of the particles are the finest particles and they determine the speed of sedimentation of this mineral, as well as its rheological behavior. The reported results were adjusted to the granulometric distribution model [16] and are shown in Table 2.
, they are the ones that gives plastic properties to the pulps. There is a predominance of fine fractions of general form and D80 corresponds to that of particles smaller than 7 µm, which indicates that 80% of the sample has a diameter smaller than this value, therefore, most of the particles are the finest particles and they determine the speed of sedimentation of this mineral, as well as its rheological behavior. The reported results were adjusted to the granulometric distribution model [16] and are shown in Table 2.
To obtain the values of shear stress, an arithmetic arerage of the three replicates was determined for each velocity gradient with its standard deviation and coefficient of variation did not exceed 5%. From plotting the values of shear stress and velocity gradient all the samples describe the Bulkley-Herschell pseudoplastic model, the rheological parameters are obtained (initial shear stress, consistency index and flow index) with the help of the computer application for the modeling of the flow curves.
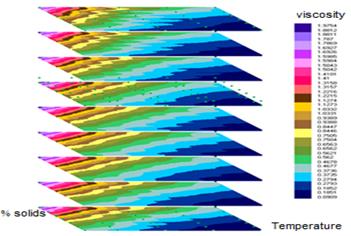
Due to the need to obtain adequate prediction of the rheological parameters for whatever the measured values of solid concentration, temperature in the actual production process, it is proposed the use of the method called UPD [33-36], analogous to the method of Radial Base Functions [37] and the Kriging method [38].
For this modeling the standard parameters of the method were taken: distance power p=1, distance smoothing factor δ=0 and derivative ε as the arithmetic average of the dependent variable, in each summation the Euclidean distance appears.
between the coordinate Pi = (Xi2; Xi3; Xi4) of a data and the coordinate of the point where we will estimate Pe=(X2; X3; X4), as shown in the isofranjas of Fig. 4.
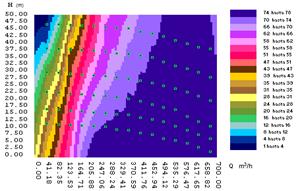
The following mathematical models are proposed that will allow obtaining the operating point in correspondence with the flow requirements of the centrifugal pump. These models are obtained taking into account the nomograms of the installed centrifugal pumps [39], see Fig. 5.
Mathematical minimun squares models obtained from the analysis of the nomogram:
With correlation coefficient equal to 0,95.
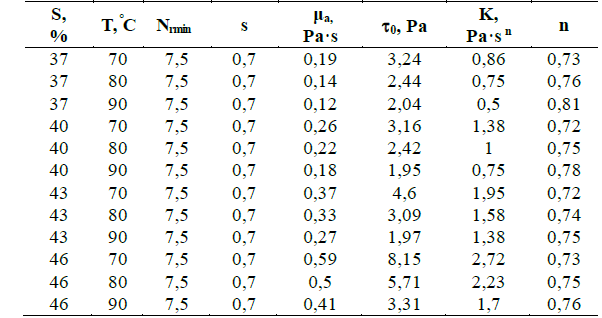
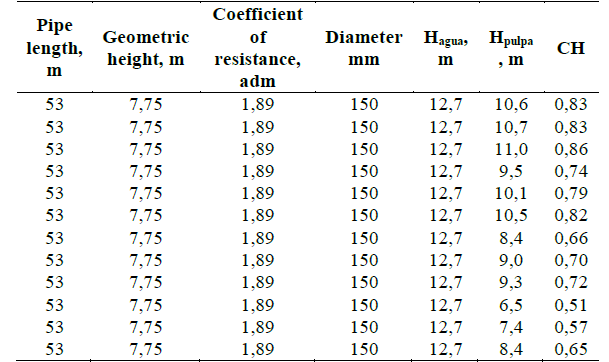
To determine the mathematical model of the correction coefficient, the data of rheological factors and parameters were taken into account, Table 3, and the characteristics of the hydraulic network were also considered.
Following the procedure shown in Table 4, a summary of the results of the experimental runs in the installation of hydrotransport.
With the experimental database a mathematical model of minimum squares is obtained that allows the correction of the characteristic curve of the centrifugal pumps that transports lateritic hydromixes.
With correlation coefficient equal to 0,97.
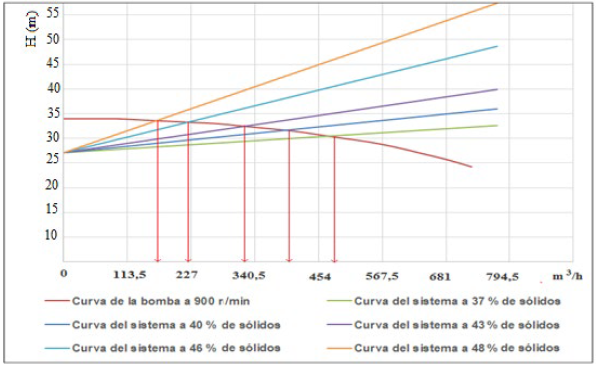
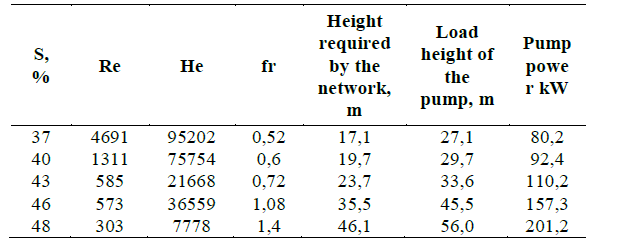
Taking as reference the results of the mathematical models of the rheological parameters [40] and the models of the energy parameters of the pump, the operating point of the centrifugal pumps is determined for different concentrations of solids under the current operating conditions, The designed extraction flow of the TK1 tank is 454 m3/ h. see Table 5.
For n = 900 r/min, it can be seen in Fig. 5, the flow is reduced to a concentration of 46 % up to 227 m3/h, which causes losses in the production it does to not guarantee the productivity of the Leaching Plant with a contribution of 1600 and 1800 t/day of ore for each thickener tank, in addition the electric power consumption is increased due to the longer pumping time.
As shown in Fig. 5, the speed of the pump changes as it is necessary to obtain the flow Q1 at a height Hd, currently this is not achieved because the variable speed drive is set at the speed of 900 r/min, because the dynamic height incorrectly selecting and not having a load correction coefficient of the lateritic pulps at different concentrations of solids.
3.1. Operation of lateritic hydromixes pumping systems
The main results of the procedure proposed in Table 6 are presented, it can be seen that for different concentrations of solids and rheological parameters there is a variation of the characteristics of the parameters of the hydraulic network with a higher pumping power to guarantee the desired flow rate.
In Table 7, it can be seen that as the temperature increases, less pumping power is required and this is precisely due to the influence of temperature on the rheological parameters of the pulp, the values of apparent viscosity and initial shear stress decrease. , it is verified that the lateritic hydromeccle at high temperature increases the flow index, without becoming a Newtonian fluid.
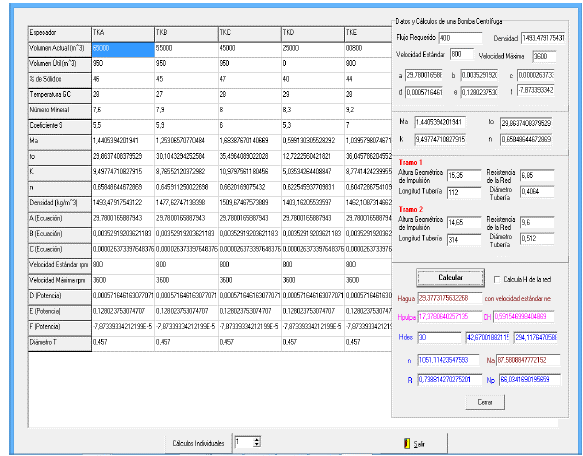
In order to implement the results of the mathematical models of the rheological parameters and the operation of the pumping system in the technological and research practice, it is necessary to design and develop a computer application Fig. 6, which automates the main procedures, which has been designed and programmed in Delphi 7.0 [41]
To ensure the daily productivity of the Leaching Plant, 9,000 to 10,000 t /day of ore are needed, equivalent to 375 and 417 t/h. To achieve this, between 1600 and 1800 t /day of each thickener must be extracted, the centrifugal pumps must have an extraction flow of 450 to 478 m3/h and a concentration of solids that is achieved in the thickener cone, according to the sedimentation rate which corresponds to the deposits in exploitation.
It is characterized a typical situation of the operation with 5 thickeners in operation, with the current volume, the useful extraction volume, the% solids, the enviromental temperature, the rheological parameters and the density. If the characteristics of the fluid to be transported and the characteristics of the hydraulic network are taken into account, from the bottom of the TKA to the storage tanks, the load correction coefficient obtained by the mathematical model of the lateritic pulp that relates the concentration of solids, the temperature and the mineral number, which allows to obtain the load and power models for the operating conditions Table 8.
It is evidenced in Table 8 that the extraction power for Thickener F, is not made and for Thickener E it is 273,07 m3 /h, for these two Thickeners the distance is higher than 800 m, so he has to overcome greater height; in the case of TKE it is 49.61 m.
The concentrations of solids that are in the TKA with 46% and TKC with 47 % would be the highest that can be reached, with these conditions the pumps with speeds above 1000 r /min achieve the desired extraction flow.
In order to effectively design and operate the equipment of the hydrotransport facilities, the correct selection of pumping equipment is necessary for the specific conditions of operation, determination and analysis of the working regime of the pumps in correspondence with the required conditions and, when considering minimum Electricity expenses they influence on the technical-economic indicators.
4. Conclusions
The mathematical models of the rheological parameters of the lateritic hydromezclas and of the energetic parameters of the pumping systems studied were obtained and evaluated according to the factors: solids concentration, temperature, chemical and granulometric composition. For the variable characteristics of the aforementioned factors, the knowledge of these models constitutes the knowledge base to guarantee the required flows in optimum energy operation regimes of the Leaching Plant.
From the variants of the operation of the pumping system of crude lateritic pulps it is possible to increase in no less than 2% the transport of solids when the rheological characteristics of the pulp are taken into account, with an average increase in the production between 1000 -1500 tons of Ni + Co / year and an electric energy saving of 30 MWh / year. Obtaining a model of the correction coefficient as a function of the concentration, temperature and number of ore in the pulp allows the implementation of corrections for the operational characteristics of centrifugal pumps when transferring viscous fluids of a non-Newtonian nature. These modifications increase the possibilities of analysis and selection of pumping equipment that transport pulps.