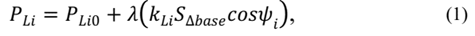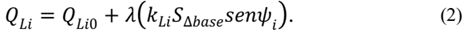1. Introduction
A stable power system must maintain voltage magnitudes at all buses with acceptable values during the normal operation and after disturbances [1,2]. Therefore, voltage stability studies are useful to identify the operation states of the power system by obtaining voltage stability curves (VSCs) and voltage stability indices (VSIs). However, finding multiple VSCs that relate the maximum real and reactive powers allowed in a load bus according to the changes in generation, network elements, and different load conditions is not an easy task because of the number of possible combinations that all changes may generate. All this complicates the understanding of the voltage stability phenomenon, as well as visualizing the power system operation risks.
Several voltage stability analysis methods have been proposed in the literature to identify voltage stability limits (VSLs) and voltage stability margins (VSMs) [3,4]. Some are based on mathematical methods that use power flow (PF) or network equivalent to find VQ and PV curves [2,3]. In 1992, the continuation power flow (CPF), which used a tangent vector of a prediction and correction algorithm to find the stability limit, was presented [5]. In 1997, PQV curves were used to represent the voltage magnitude variation with respect to the real and reactive powers of loads [6]. In 1997, the network equivalent method was used to obtain the PV curves and define an index of proximity to voltage collapse [7]. In 1998, some curves were used to find the stability limits after contingencies and define strategies of minimum load shedding [8]. In 2004, a hybrid CPF-based nonlinear prediction for the upper curve at the points near the limits and the linear prediction for the lower part of the curve of a load bus were proposed [9]. In 2004, the equivalent network method was used to study voltage stability, obtaining PQ curves using the mathematical technique of the probability rectangular distribution function of load [10]. In 2005, the CPF was used for three-phase unbalanced power systems [11]. In 2006, PMU measurements were used to estimate the network equivalent in a bus and obtain PV curves and VSL [12]. In 2010, a new voltage stability index was obtained from PQV curves of a bus, an area, or the power system to classify buses and areas [13]. In 2014, a method to obtain PQV curves based on network equivalents was presented [14]. In the same year, the maximum load factors of the load and the maximum power reserves of generators were used to determine PV and QV curves [15]. Metaheuristic algorithms are techniques that can find the maximum limit of load as presented in [16], which considered hybrid differential evolution and particle swarm optimization.
Most of the techniques found in the literature are used to find a few VSCs considering a predefined load and generation variation. This is because conventional techniques require much time to create a large number of points to determine voltage stability regions (VSRs) by increasing real and reactive powers, and they use more computing resources. This leads to the conclusion that better voltage stability analysis techniques must be developed to evaluate all the possible operation risks and avoid voltage instability and collapse.
According to the described problem, this article seeks to generate fast two- and three-dimensional curves that represent the steady-state stability of the power system. The calculation is done considering changes at the real and reactive powers of loads and generators. In addition, the maximum real and reactive powers consumed by loads according to different contingencies of the elements in the power network are determined by the method. This problem was formulated as multiobjective optimization based on finding the maximum real and reactive powers of load and generation. Combination with the voltage magnitudes can easily generate different VSC, such as PV, QV, PQ, and PQV.
The cuckoo search algorithm (CS) is used to generate changes in the real and reactive powers of generators and loads to determine the VSL, VSM, and VSC for normal operation and contingencies. This algorithm is integrated into the Newton Raphson (NR) method to calculate PF and assess the multiobjective function. Fast non-dominated sorting (FNS) and crowding distance (CD) techniques allow classification of each point evaluated on different VSCs, finding the different limits of real and reactive powers at a certain load bus, several load buses in areas, or all loads in the power system.
2. Methodology
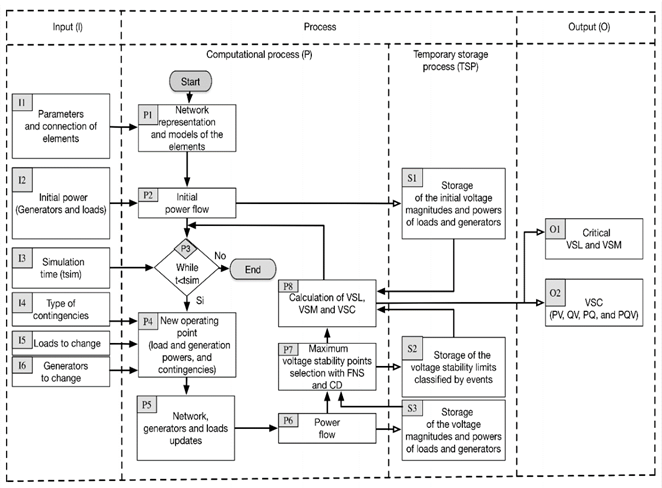
Fig. 1 shows the methodology used to find multiple VSLs, VSMs, and VSCs. This procedure was implemented in the MATLAB programming language and integrated with the Power System Analysis Toolbox (PSAT) and MATPOWER to use the algorithms PF and CPF and validate the functioning of the method in both toolboxes. Below, we describe the input values, the procedure, the stored values, and the output values.
2.1. Input values
The input values defined in Fig. 1 are the parameters and connection of the elements in the power network (I1), the initial power of loads and generators (I2), the simulation time of the algorithm (I3), the type of contingencies (I4), the loads to change the real and reactive powers (I5), and the generators to change the real and reactive powers (I6).
2.1.1. Parameters and connections of elements (I1)
These data are used to build the power system under study. For this research, the IEEE 14-bus power system test case was used [17]. The connections of the elements and their parameters are entered using a text file, with the same structure of the input data for PSAT or MATPOWER. For lines and transformers, the series and parallel impedances and admittances are defined to build the admittance matrix of the power system.
2.1.2. Initial power (generators and loads) (I2)
These are used to calculate the initial operation of the power system. Real power, reactive power, and voltage magnitudes are defined for buses with loads and generators. These parameters were taken from the IEEE 14-bus power system test case found in both PSAT and MATPOWER.
2.1.3. Simulation time (I3)
The user can define the time to calculate the VSLs, VSMs, and VSCs. Because the problem requires generating a large number of curves, a longer time is needed to obtain graphics with better resolution. It is recommended that the users know each scenario well to establish the time required to evaluate different combinations of real and reactive powers of loads and generators and to select the critical contingencies.
2.1.4. Type of contingencies (I4)
A list of contingencies can be defined as an input to evaluate the condition states after disconnecting generators, transformers, lines, and loads. Although the algorithm assesses all contingencies of the power system, it is recommended to determine the most critical events to save time during the evaluation of all possible changes in the network.
2.1.5. Loads to change (I5)
The number of loads to change must be defined by the user to represent the different real and reactive powers consumed during the operation of the power system. The real and reactive powers of loads can be changed in a single bus, a group of loads in areas, or all buses of the system load.
2.1.6. Generators to change (I6)
The number of generators to change must be defined by the user to represent the different real and reactive powers supplied by the sources during the operation of the power system. The algorithm will search for multiple combinations of real and reactive powers of generators to evaluate the risk of collapse.
2.2. Processing
The process presented in Fig. 1 can be divided into two parts. The first part corresponds to the calculation of the initial values of the power system (from P1 to P2). The second part corresponds to the calculation of the VSL of the power system (from P3 to P8).
2.2.1. Network representation and models (P1)
In this step, the elements of the power system and their interconnection models are included. The load was modeled as a static power supply, meaning that the real power and reactive powers are fixed during the evaluation of each PF. The models used for the representation of generators are constant real and reactive powers (PQ), constant real power and voltage magnitude (PV), and real and reactive power compensation (slack). Lines and transformers were modeled as constant admittances that allow the creation of the Y bus matrix of the power system.
2.2.2. Initial PF (P2) and initial data storage (S1)
An initial PF with the NR method is calculated to obtain the values that will be used by the algorithms that assess the voltage stability of the power system. The resulting values of the PF are stored in solution arrays considering the voltage magnitudes of buses, the real power, and the reactive power for all generators and loads.
2.2.3. Execution time (P3)
With the simulation time defined by the user (I3), the algorithm will run until the time is completed and the algorithm finds voltage stability solutions. As previously stated, the time can be modified by the user to define the running time according to the scenario studied for each power system.
2.2.4. New operating point (P4) and updating the data (P5)
At this point, the algorithm receives the combinations of real and reactive powers of loads and generators as well as contingencies. All these values are used to evaluate the operation and find the VSLs, VSMs, and VSCs. The changes in the real and reactive powers of each load or generator are modeled through the use of the parameter of change λ as shown in eqs. (1) and (2)[5].
In eq. (1), P Li is the new real power calculated for the load at bus i, P Li0 is the initial real power of the load at bus i, and λ represents the changing parameter of the power, created randomly by the algorithm. The term K Li is a multiplier to designate the rate of load changes at bus i [5] and S ∆Base is a quantity of apparent power used to scale the real and reactive powers. In eq. (2), Q Li is the new reactive power calculated for the load at bus i and Q Li0 is the initial reactive power of the load or generator at bus i. Therefore, combinations of real and reactive powers of load buses are obtained through the generation of different values obtained with eqs. (1) and (2). This formula can be also modified to represent the generation or network changes, using λ to increase or reduce the real and reactive powers [5].
Changes in the powers of the loads, generators, and network elements are created randomly by a metaheuristic algorithm. This algorithm can generate a large number of points and select the best solutions. Recently, many algorithms have been presented: particle swarm optimization, ant colony, an evolutionary algorithm, simulated annealing, a bat-inspired algorithm (BA), and harmony search (HS) [18-20]. BA, HS, and CS algorithms have been tested to solve multiobjective problems of electrical engineering [19], and although FNS and CD have been used for various problems [21], they have not been applied for voltage stability analysis. In this work, the CS algorithm is used to generate the different powers of load and generation and contingencies.
2.2.5. Power flow (P6) and data storage (S2)
A new PF using the same NR method is run to evaluate the changes made to the power system. Each change is evaluated to determine the operating state, and all the results are stored in a solution array.
2.2.6. Finding the limits (P7) and storing the values (S3)
This part of the methodology corresponds to the innovation of this proposal because we use FNS and CD combined with a PF to select multiple operating points that correspond to the maximum real and reactive powers or the minimum voltage magnitudes in the critical operating limits. This method finds fast multiple limits because if all previous solutions meet the criteria shown in eqs. (3), (4) and (5), then they are considered for the next evaluation [22]:
where P Li , Q Li , and V Li are the maximum real power, reactive power, and voltage magnitudes, respectively, found previously by the algorithm (P6) and stored in a solution array (S2). The terms P * Li , Q * Li , and V * Li are the maximum real power, reactive power, and voltage magnitudes selected, respectively, because they dominate the solutions of the given array in S2 [22]. The “greater than” symbol in eq. (5) is used to generate several points in a three-dimensional VSC forming the complete VSR, or this term can be changed to “less than” to find only the VSL in a three-dimensional VSC. The new points found by the proposed method as the maximum real power, reactive power, and voltage magnitudes represent the multiple Pareto fronts to analyze voltage stability [22]. The new results are stored in a new solution array (S3) and subsequently used in the calculation of the voltage stability.
The FNS and CD algorithms select solutions by Pareto dominance and classify them on different fronts found according to their quality as described in [23]. A Pareto front is created to characterize the maximum loadability of the system. The structure of the algorithm consists of the generation and selection of points that are part of the boundaries. The fast evaluation and selection consist of generating multiple possible points at the limits or the Pareto frontier, representing the risk of the operation of the power system.
The crowding-distance assignment parameter calculates the separation between a particular solution and its nearest neighbors’ solutions, such that selecting those with a greater crowding distance preserves the diversity of solutions in the NSPF as established in [23]. This technique is based on calculating the perimeter of the parallelepiped, in which the vertices are the two neighboring solutions, the previous and subsequent solutions, of a particular solution. If the solution differs from the rest of the solutions, the perimeter of the previously mentioned parallelepiped will be greater than in the case in which the solution contributes only slightly to the diversity of the Pareto front evaluated.
2.3. Output values
The output values obtained from the processing are the critical VSL and VSM (O1) and the VSC (O2). Next, we describe each output value obtained by the proposed algorithm.
2.3.1. Critical VSL and VSM (O1)
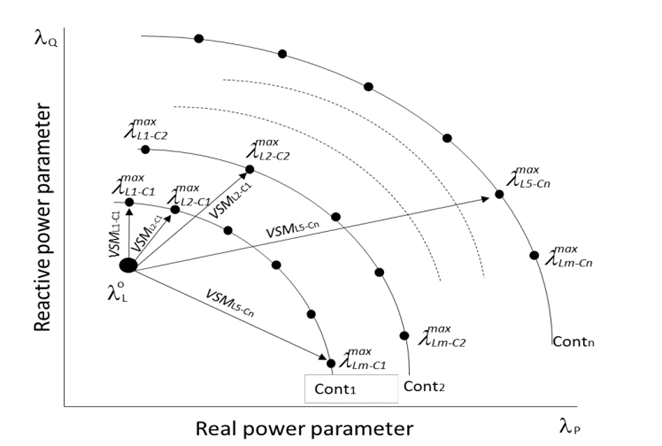
The VSLs and VSMs are found by the algorithm, representing the operating risk from the starting point to the limits as shown in Fig. 2[1]. In this figure, the parameter λ i max is the maximum load at bus i, λ i 0 is the initial load at bus i, VSLi is the voltage stability limit at bus i, and VSMi is the voltage stability margin at bus i. As multiple VSMs can be calculated by measuring the distances from the initial operating point to the multiple maximum VSLs, the critical margin and limit are selected from the minimum distance obtained in the simulation.
2.3.2. Voltage stability curves (O2)
Multiple VSCs can be drawn at the same time with this method because the algorithm classifies the results according to the multiple changes created and evaluated. As an example of the curves obtained by the method, we can draw two-dimensional PV, QV, and PQ curves and a three-dimensional PVQ curve. The user can define whether the curves are represented or only the VSL.
Fig. 2 shows some PV curves, which represent the voltage magnitude variation with respect to the load parameter λ i at bus i. This load parameter λ i PV and PQ curves of the power system for different power factors. The combination of load, generation, and contingency parameters creates multiple VSCs for each load, area, or power system. When the number of combinations increases, the number of curves to draw is larger. Therefore, evaluating the risk of collapse can be a difficult task when using conventional methods.
The PQ curves represent the VSRs as real and reactive power values of the maximum load consumption and generator supply from a bus, area, or power system. Fig. 3 shows the operating point and the maximum real and reactive power consumption in a bus of the power system, where λ L 0 is the initial parameters of load and generation, calculated using the initial PF in P2 and stored in S1. This curve shows the VSL and VSM calculated for each contingency in the power system.
The values of λ L max correspond to the maximum real and reactive powers of load and generation because of contingencies, calculated using procedure P7 and stored in S3.
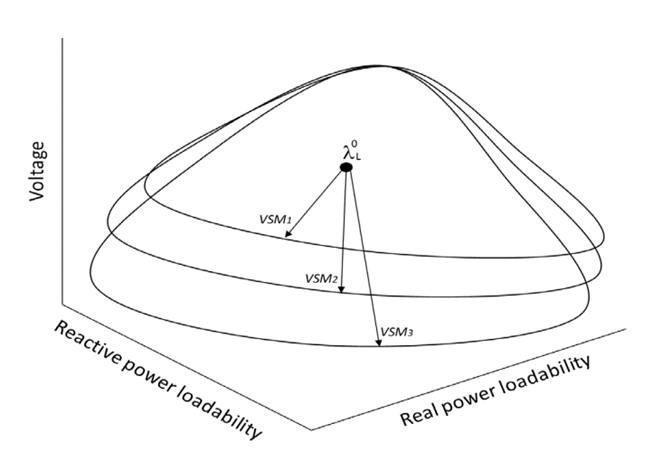
Fig. 4 shows three-dimensional curves used to display the voltage changes according to the variation of the real and reactive powers of loads and generators. The regions can be created for a load bus, different loads in an area, or the entire system. This figure illustrates the operating point λ 0 L in the stable region, the different voltage boundaries, and multiple critical VSLs in different layers, which represent the risk of operation. VSM 1 is the voltage stability margin measured from the operating point to a maximum point in layer 1, VSM 2 is the voltage stability margin measured from the operating point to a maximum point in layer 2, and VSM 3 is the voltage stability margin measured from the operating point to a maximum point in layer 3. Multiple layers with all the VSLs can also be determined by the algorithm to evaluate the risk of different changes in the power system.
3. Results and analysis
This section presents the results of the NSPF to quickly calculate multiple VSLs, VSMs, and VSCs. Using the multiobjective optimization method, several curves can be plotted simultaneously, changing the real and reactive powers of a single bus, some loads in an area, or all loads in the power system.
3.1. Power system test case
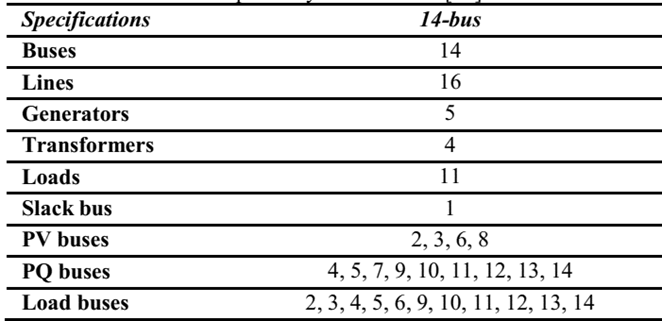
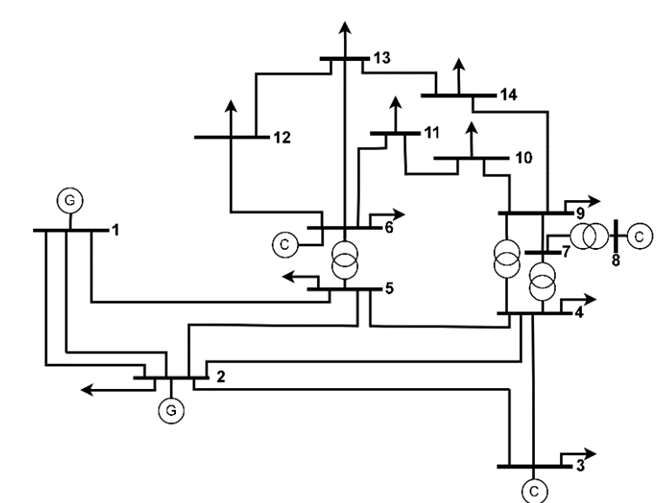
The selected test case was the IEEE 14-bus power system, regarding which general information is shown in Table 1, and the single diagram is shown in Fig. 5[17]. The total real and reactive powers of the load are 392.05 MW and 205.54 MVAr, respectively. The total real and reactive powers of generation are 362.6 MW and 113.96 MVAr, respectively.
3.2. VSL and running time
Conventional voltage stability analysis methods find VSCs and VSIs; however, users must define the power magnitudes of the load to increase and the buses to apply changes and contingencies. The NSPF assesses a large number of conditions of the system such as changes in load, generation, and contingencies at the same time. The evaluation of critical events represents a good option to identify the operation risk of the power system while reducing the simulation time required to analyze multiple possible combinations.
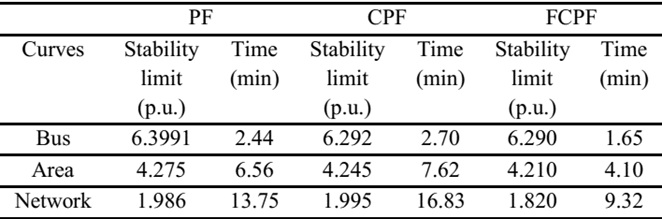
Table 2 shows a comparison of the PF, CPF, and NSPF to assess the critical VSL in a bus, area, or the power system. To perform this comparison, it was necessary to define a few previous operation cases to solve them by conventional methods because these methods do not automatically perform all possible cases according to the power changes. For the study, we consider bus 14, for the area buses 12, 13, and 14, and for the power system all loads (load buses are shown in Table 1). We also considered finding 200 points for the bus, 600 points for the area, and 1,200 points for the power system.
Table 2 shows that the NSPF method obtained the most critical limits that represent the operation risk, and the execution times were shorter. The PF and CPF methods take longer to find closer values because the search for the solution is limited to the rank that the user defines and the increasing power of loads is fixed. For a single bus, the calculation times do not differ much; however, when the problem becomes larger, the number of combinations makes a big difference in the solution time. With respect to the VSLs, the three methods have similar results because the search is focused on a selected and limited zone; however, when the size of the problem increases, the PF and CPF algorithms take a long time to find similar solutions.
3.3. Critical VSL and VSM
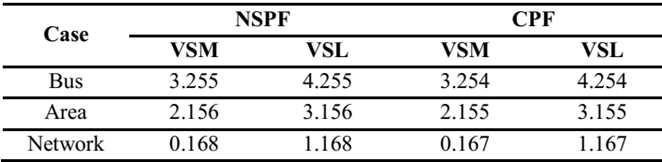
The proposed algorithm assesses multiple evaluations for defining the most critical VSIs that represent the risk of the power system operation. The search is performed on a large number of combinations. The search is performed by the change of real and reactive powers of loads and generation and the contingencies of the network. Table 3 shows the results found by the proposed algorithm after evaluating multiple changes in the real and reactive powers of loads and generators and critical contingencies. Because conventional algorithms do not find this combination, the comparison is done by evaluating the same case study found by the proposed algorithm to determine whether it has a good accuracy. Comparison with the CPF method was used only to identify the accuracy of the solution because this method does not automatically evaluate all the possible solutions. For the study, we consider bus 14, for the area buses 12, 13, and 14, and for the power system all loads (load buses are shown in Table 1).
After validating the best value for the CPF, the results show that the proposed method provides good accuracy for finding VSL. However, one limitation found with the proposed method is achieving the best accuracy for all VSLs, so more research is needed to identify a better method.
3.4. PV curves
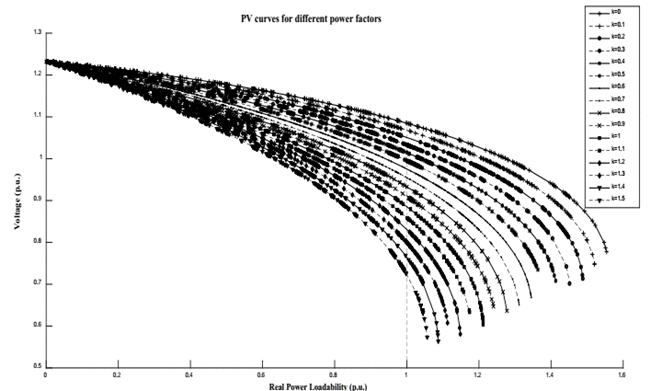
Fig. 6 shows the PV curves created with the NSPF, considering the multiple variations in the real and reactive powers of loads and generators. All the points are plotted simultaneously by calculating random values, and then they are classified according to the relationship between real and reactive powers (k = Q/P), which can vary between 0 and 1.5. Similar curves can be created for different buses, areas, and the power system as well as to evaluate multiple contingencies in the power system.
This figure shows that the PV curves were plotted for a large number of points calculated and classified for different stability curves, according to the power factor. Each curve was created starting from the unloaded system to the VSLs. Furthermore, the NR method used in this research loses accuracy when approaching to the VSLs, which can be improved in future work using other calculation techniques.
3.5. PQ curves
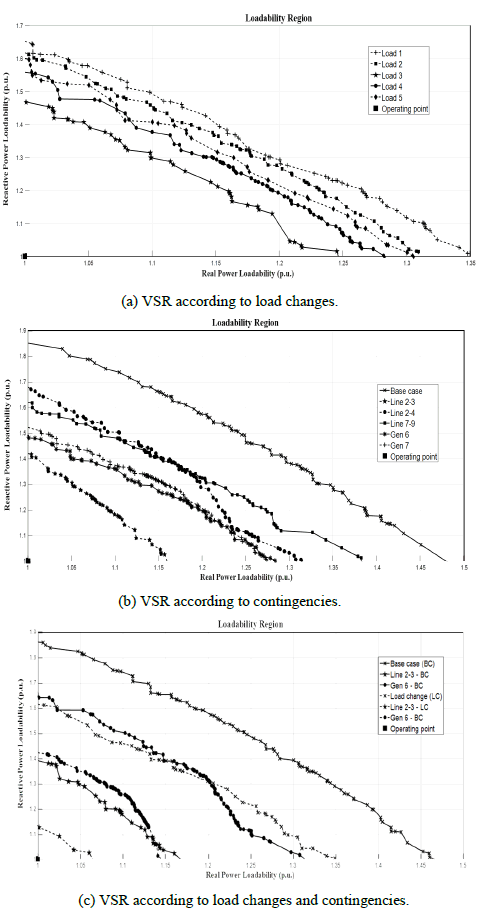
Fig. 7 shows the voltage stability regions represented by real and reactive power curves (PQ curves or VSRs), according to the critical contingencies. These curves represent the voltage collapse risks evaluated for different operating conditions of the power system. Using this method, we can create the loadability region VSR of a bus, an area, or the power system. Each region represents an operation layer for a load change, where the maximum operation is formed by the VSL. This evaluation can be performed with random load and generation variations, representing the stochastic changes of separate loads. We conducted five minutes of simulation to determine multiple points in all curves.
Fig. 7(a) shows that new VSRs can be obtained after load and generation change. We formed PQ curves for five load and generation change cases, obtaining the VSL that evaluates the risk of the changes in the same iteration process. This is useful to evaluate how each loadability change can affect the operation of the power system. The importance of this method is that different directions of loadability for each bus can be programmed to evaluate how the different load changes affect VS. In this figure, some load changes result in the operating point coming closer to the VSL.
Fig. 7(b) presents the evaluation of five selected contingencies to determine different VSLs. For this case, we considered the initial load and determined how different events can be plotted and selected during the same iteration while considering different changes in load and generation. For this study, the real and reactive powers of all the loads and generators in the power system changed. The figure shows how some contingencies cause the operating point to approach the VSL.
Finally, Fig. 7(c) shows the operation behavior under two load study cases and two contingencies in the power system. The first load case is the power system without modifications (the base case). The second load case is a random load increase represented by the maximum and minimum individual load changes in real and reactive powers. The curves show that load 2 is more critical for operation because the outage of line 2-3 is a critical case for voltage collapse, followed by the risk that represents the output of generator 6. In the same way, multiple loadabilities can be studied to determine those most critical for the network.
VSL and VSM can be calculated from the operating point to the maximum values represented at each VSC. The most critical VSM and VSL can be classified according to the event as the minimum magnitudes of VSM. This method is useful to classify the severity of contingencies before and after the power load or generation change in an identified direction. The algorithm creates multiple curves and evaluates the different risks that the power system can be subject to in the same iteration process.
3.6. PQV curves
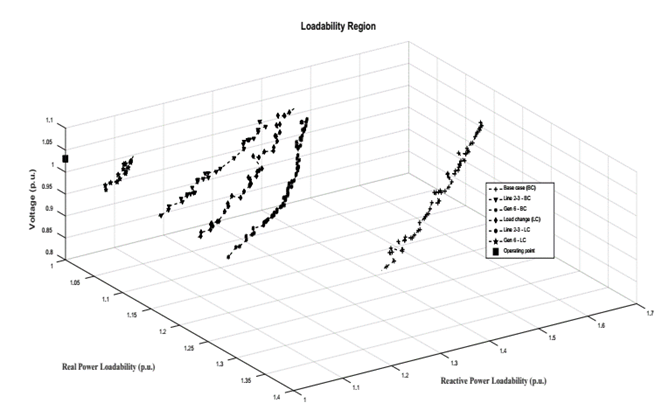
Fig. 8 shows the three-dimensional curves plotted for bus 14. In the figure, the voltage magnitudes with respect to the real and reactive powers are represented. The curves can be created for different contingencies, forming multiple layers according to the direction of load and generation changes. The number of points in the curves is plotted according to the simulation time defined by the user as explained in procedure I3. The VSL and VSM are calculated with the maximum real and reactive powers, obtaining different operation risk according to the layers evaluated. From an initial loadability or a changing loadability direction, we can evaluate multiple risk points while considering various contingencies and increases in loads and generation.
Fig. 8 also shows the separation between the normal operating point and the layers with VSL in six critical VSRs. VSL and VSM can be calculated from the operating point to the maximum values represented at each three-dimensional VSC. The base case (BC) shows that the operating point is far from the critical values. However, the contingencies “Line 2-3 - BC” and “Gen 6 - BC” show that the operation is under risk. When the load increases and the operating point moves from the initial value, the new VSLs are closer to the operating point. Therefore, when the load increases, any contingency results in a worse condition for the power system, as for contingency “Line 2-3- LC” (not plotted because the power system operation collapsed). For this new loadability of the network, the contingency “Gen 6 - BC” represents a high risk for the power system. Similarly, the evaluation can be performed for any new loadability in the power system, thereby identifying the operation risks that multiple events represent for the power system.
4. Conclusion
This work presented a voltage stability assessment method that uses the FNS and CD integrated with a PF. This method calculated the maximum limits of multiple possible changes in loads, generators or network elements. Furthermore, this method obtained critical VSLs, VSMs, and VSCs such as PV, QV, PQ, and PQV for a bus, an area, or the power system. Using this method, it is possible to identify multiple VSRs and evaluate multiple voltage collapse risks according to the real and reactive power changes in load and generation for normal operation and after contingencies.
The most critical VSLs and VSMs of different possible changes in the power system were calculated in the shortest simulation time with NSPF compared with the time required for evaluating multiple alternatives with the PF and CPF methods. With this method, we can create a large number of curves defining ranges of solutions, the contingencies, and the load or generation power can vary to simulate multiple events that occur in the power system. In addition, graphic representation of multiple VSCs, such as PV, PQ, and PQV, can be plotted simultaneously, representing the operation risk for the voltage collapse.
In future work, we will work on different methods that recognize the influential areas for voltage stability in power system. In addition, we will be investigating new techniques for voltage stability assessments to reduce simulation time and improve the accuracy in the VSL.