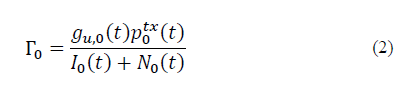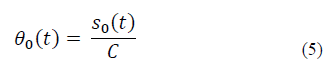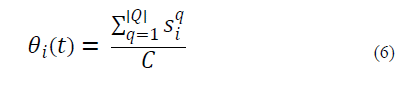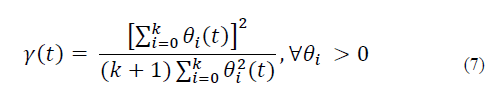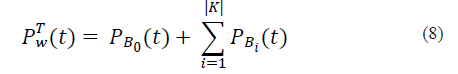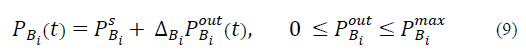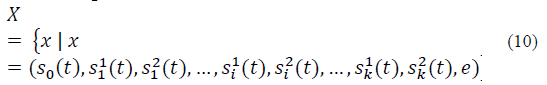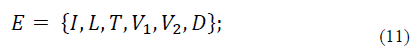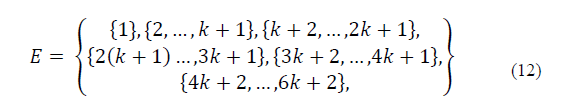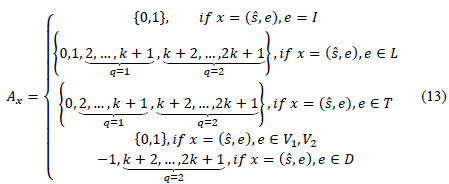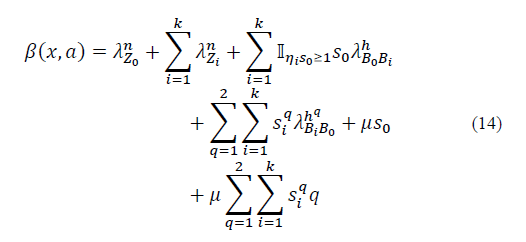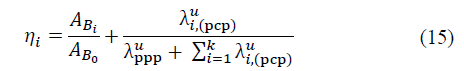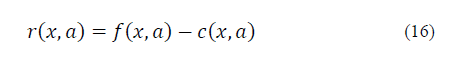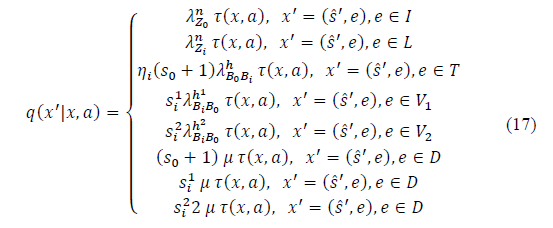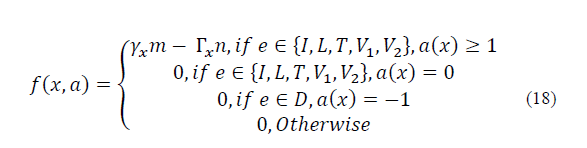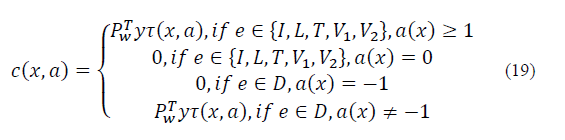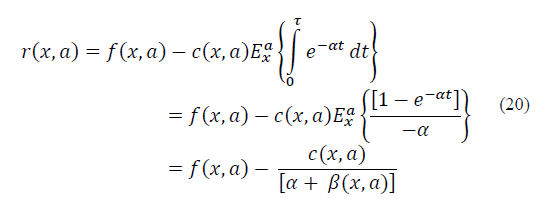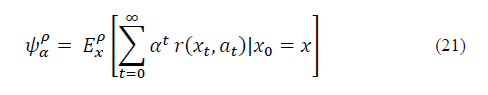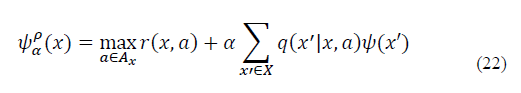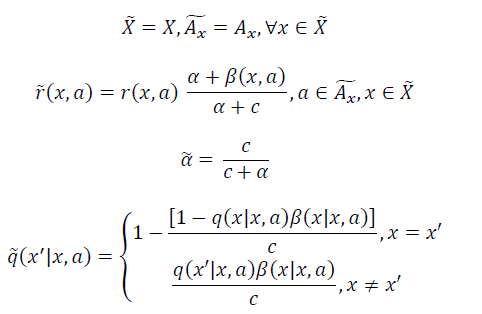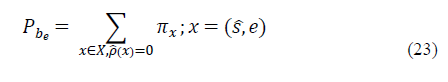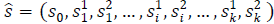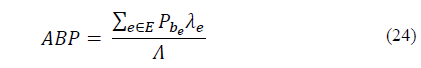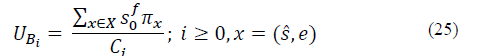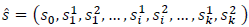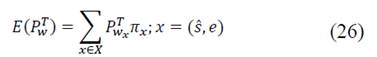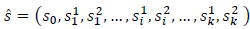1. Introduction
The importance of the RAN selection process in Heterogeneous Networks (HetNets) and its effect on system performance has been widely acknowledged [1]. Hence, the design of RAN selection and resource allocation policies is considered a major challenge in the deployment of HetNets [2].
On the other hand, another important aspect to take into consideration for the analytical performance of the RAN selection process and resource allocation strategy in two-tier HetNets is the fact that small cells (SCs) are being deployed in zones with high density of users in order to satisfy the demand generated in hotspot areas. As such, this scenario represents a radical shift in the way that cellular networks were traditionally analyzed, moving from macro cell-driven architectures to user-centric capacity-driven network architectures, in which base stations are deployed to serve clusters of users [3]. For this reason, new proposals must consider and analyze scenarios where the user distribution is related to the spatial location of base stations, taking a completely different view from previous analyses, where users are assumed to be uniformly distributed. In particular, inspired in the work introduced in [3], and with the aim of deriving some useful metrics for the decision making process, we modeled the location of users clusters correlated with the location of SCs using the stochastic geometry framework.
In this article, we study RAN selection and sub-channel resource allocation for the downlink of a two-tier HetNet system under co-channel and user-centric deployment. In this context, it is well known that radio resources constantly change over time, and decisions related to the use and management of these resources will have an impact on future outcomes as well as on the system behavior (i.e., it affects performance metrics such as blocking probability and network utilization). We propose a joint decision-making strategy for these two radio resource management (RRM) functions.
The main goal of the strategy is to achieve the optimal expected long-term discounted reward. We define the reward function as the income earned by the fairness level of the session distribution between the MC and the set of available SCs, the level of signal-to-interference-plus-noise ratio (SINR), and by the level of power consumption at a specific instant of time. Thus, when an incoming session (i.e., new or handoff) is accepted, a reward is assigned. On the other hand, if the incoming request is rejected, no reward is assigned. Likewise, when a session abandons the system, there is no compensation. However, at these points, our model proposes to incorporate a traffic distribution process. The main intention with this process is to evaluate the possibility of introducing an offloading process, i.e. to move an ongoing session that is being served by the MC to one of the SCs that has the capacity to host it. Essentially, this is a network-controlled process, which has an associated cost with its execution. In the scope of this work, more bandwidth (i.e., sub-channels) will be assigned in the SCs for the offloaded sessions.
In this scenario, we formulate a discounted SMDP-based approach for the RAN selection and sub-channel allocation in a HetNet. This strategy is designed with the aim of improving the overall performance of the system in terms of achieving a better usage of radio resources, a lower blocking probability and to contribute to decrease the power consumption. To solve the SMDP model and obtain the stationary optimal policy, we used the value iteration algorithm (VI) [4].
In this order, it is important to investigate the impact and the trade-off of the RAN selection and resource allocation decisions in the performance of the system in terms of the overall radio resource usage, the blocking probability, and the energy consumption. To evaluate the effectiveness of the proposed framework with regards to the performance metrics aforementioned, we have carried out a numerical evaluation and a comparison against greedy and random approaches.
1.1. Contributions
In comparison to the state of the art, the contributions of this work are summarized as follows:
The RAN selection and sub-channel resource allocation in the downlink of a two-tier HetNet system under co-channel and user-centric deployment are analyzed as a sequential decision-making problem. In this respect, we use SMDP as the mathematical framework to model the optimization problem and employ value iteration algorithm to solve it. This article focuses on the use of SMDP to model and obtain an optimal stationary policy for the RAN selection and the resource allocation problems in a two-tier HetNet.
Under our SMDP analysis for the RAN selection and resource allocation optimization problem, we evaluate the feasibility to perform an offloading process when a session departure takes place. The goal is to reduce the level of the load of the MC as well as to improve the overall resource use while achieving a lower blocking probability in order to guarantee good levels of QoS. As a direct consequence of the lower use of the MC, a lower power consumption is expected.
A differentiating aspect of our work is that we obtained an optimal network selection and resource allocation strategy offloading policy by considering the correlation between the SCs location and the user cluster in the downlink of the two-tier HetNet.
We compared the proposed strategy against two baseline schemes, specifically greedy and random approaches for the RAN selection and resource allocation problem. Numerical results show the performance and effectiveness of the proposed strategy in comparison to these baseline approaches.
2.2. Organization of this paper
This article is organized as follows: we introduce the network, traffic, and channel models in section 3. After that, an overview and a definition of metrics for the decision-making process are introduced in section 4. Next, in section 5, we described the proposed SMDP based model. Performance metrics as well as the results are defined and presented in section 6 and section 7, respectively. Finally, a summary and conclusions of the paper are illustrated in section 8.
2. Related work
The resource management problem in heterogeneous networks has been previously investigated in the literature. In this sense, the solution method employed has been studied from the modeling and architectural points of view, and also by considering different scenarios for evaluation purposes. This section presents a summary and a comparison of the works related to this article.
In [5], the main goal is to minimize the total power consumption of an OFDMA HetNet system that suffers interference, while satisfying user demands in terms of data rate. The authors solve the model by implementing iterative optimization algorithms, and the numerical results obtained show their effectiveness. The set of strategies that we propose in this article differ from this work as follows: On one hand, they use classical optimization methods, which consider a static view or a snapshot of the system under analysis, whereas we are concerned about the impact of decisions on the future behavior of the system. On the other hand, we evaluate the performance of the proposed policies by taking into account scenarios where users are uniformly distributed or clustered in hotspot zones. Lastly, they do not consider the relevance of a fair usage of the overall radio resources.
The authors in [6] introduce a distributed scheme for RAN selection in heterogeneous wireless networks. The problem is formulated as a multi-objective optimization, where the main intention is to maximize the channel quality and minimize the blocking probability. By transforming the optimization problem, users are able to select the best network that offers the highest capacity and the lowest blocking probability. To solve the proposed model, the authors use the weighted sum approach. As noted, this approach does not consider the fair usage of radio resources as we do in our proposal. In addition, they do not consider the impact on the power consumption of the system.
A scheme for the resource allocation process with the aim of maximizing the weighted sum energy efficiency in the downlink of a two-tier HetNet is studied in [7]. The strategy pursues to balance the energy efficiency between the MC and the set of SCs. The problem is formulated as a nonlinear optimization sum of ratios, and a heuristic algorithm is used to solve the model. In this work, no fair usage of radio resources is pursued, and the analysis considers uniformly distributed users. Likewise, they only focus on sub-channel allocation, while we consider the inclusion of traffic offloading strategies.
In [8], the authors propose a network-assisted approach for RAT selection in HetNets. SMDP is used to estimate the network information in terms of the load conditions, which is sent to the mobile devices, who will make the final decision about which RAN will be used to transmit data. Thus, the final decision is made by the mobile user taking into account the individual preferences of each user together with the network performance. Differences between their proposal and our work can be described as follows: They assume a HetNet scenario with a co-located deployment between the MC and an SC. In our proposal, the strategy is analyzed by considering that SCs are deployed in hotspot zones. In the same way, we consider incorporating a strategy for moving ongoing sessions from the MC to the SCs with the aim of alleviating the level of load of the MC. In summary, we seek to enhance the overall usage of radio resources with the purpose of achieving a fair usage of the RANs, being energy efficient and decreasing the long-term power consumption of the system.
3. System model and assumptions
In this section, we offer an explanation of the network, channel and traffic models.
3.1. Network model
In this paper, considering the scarcity of licensed spectrum often experienced by the MNOs, a two-tier HetNet system is deployed using single carrier frequency scheme or co-channel deployment. We analyzed a scenario where MNOs have to share the complete frequency band among the MC and the set of SCs. In this sense, we consider the downlink of a typical two-tier HetNet where a co-channel spectrum sharing scheme is used. The first tier is comprised by the MC, and the second tier consists of a set of SCs. The MC is located in the center of its circular coverage area and the set of SCs is deployed underlying the MC. For each tier, we assume the same transmission power for all base stations belonging to each layer. Likewise, let B = {M υ K} be the set that represents the total of base stations that belong to the HetNet system under consideration. M = {0} denotes a singleton that represents the MC and K = {1,2, …,k} the set of SCs, where │K│ = k and │B│ = k+1. and. Index i = 0 is used to represent the MC, whereas i = {1, …, k} denotes the SC. The coverage area of each RAN is assumed to have a circular shape with a radius rBi and given by:
In addition to this, multiple zones are identified in the HetNet system. Let Z = {0,1,…,z} denote the set of zones defined by Zj Z 𝑗 , where A = ϖr2. In this sense, index j =0 is used to represent the area (i.e., Z0) with coverage only from the MC, whereas j = {1,…,z} indicates zones with coverage of both MC and ith SC (i.e., Zj, j > 0).
We assume that users are free to be attached to the MC or SCs as long as they are in an area with coverage from both base stations. Likewise, it is also assumed that SCs are deployed in such a way that they do not intersect each other. In addition, for all possible incoming sessions that arrive to the system, one or several resource units will be allocated to serve the session in the system either in the MC or in the ith SC. In this sense, it is assumed that according to the MNO's preferences, one sub-channel is allocated for those sessions that will be served by the MC, and either one or two sub-channels can be allocated if the session is hosted by any SC. Lastly, we assume that these RANs belong to the same provider, and hence are being managed under the same domain.
3.2. Channel model
In this work, we assume a co-channel deployment, where both the MC and the SCs share the same radio spectrum (i.e., the two-tier HetNet is configured to use the same carrier or frequency band). This means that both MC and SCs transmit over the same set of sub-channels. In this scenario, let C be the total available bandwidth of the above-mentioned system, which is divided into W sub-channels (i.e., the pool of sub-channels with the same bandwidth), where C = w fw with W(t) Є [0,W] fw. is considered the minimum resource unit of bandwidth to be allocated for each incoming session.
In our proposal, we consider the average SINR value of the MC and SCs. Thus, let Г0 denote the average SINR for a user session served by the MC in the two-tier HetNet at time t, which is defined as follows [9]:
Where gu,o(t) indicates the average channel-gain between user and the transmitting MC (i.e., B0) at time t, p0tx(t) 𝑡, denotes the transmit power of the MC in the downlink channel, which should satisfy
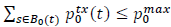 , where
, where
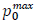 denotes the power transmission at the maximum load level, and s Є B0 (t) indicates the number of ongoing sessions being served by the MC at time t. In the scope of this paper, the parameter P0tx(t) is estimated as
denotes the power transmission at the maximum load level, and s Є B0 (t) indicates the number of ongoing sessions being served by the MC at time t. In the scope of this paper, the parameter P0tx(t) is estimated as
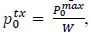 which means that power transmission on the downlink per sub-channel is the same and constant. In the denominator, the term I0(t)=
which means that power transmission on the downlink per sub-channel is the same and constant. In the denominator, the term I0(t)=
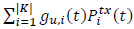 represents the average interference power from the other non-serving base stations (i.e., it is the interference caused by the other base stations). Parameter I0 is calculated by taking into account the average channel gain from the SCs to user u as well as the current power transmission of the ith SC, where
represents the average interference power from the other non-serving base stations (i.e., it is the interference caused by the other base stations). Parameter I0 is calculated by taking into account the average channel gain from the SCs to user u as well as the current power transmission of the ith SC, where
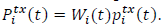 . Lastly, No(t) denotes the average value for the variance of additive white Gaussian noise (AWGN) power level. No(t) is assumed to be constant.
. Lastly, No(t) denotes the average value for the variance of additive white Gaussian noise (AWGN) power level. No(t) is assumed to be constant.
In a similar manner, the average SINR (Γi) experienced by the channel of a user associated with the ith SC is given by [9]:
where g
u,i
(t) and ptx
i(t) denote the average channel-gain and the transmission power from the i
th
SC to the user, respectively. Ii(t) indicates the aggregated average interference caused by the rest of base stations to the 𝑖 𝑡ℎ SC at time 𝑡. This interference can be computed as Ii(t)
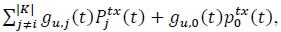 where the first term denotes the interference caused by the rest of SCs and
where the first term denotes the interference caused by the rest of SCs and
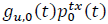 the interference caused by the MC.
the interference caused by the MC.
Different allocation profiles can be defined by the MNO. In this sense, the resource allocation profile is understood as the number of sub-channels that can be allocated to an incoming session. Let Q= {1,2,…q’} denote the set of resource allocation profiles to be used by the MNO and q= {1,2,…q’} the index to denote the number of sub-channels assigned to the incoming sessions. In the scope of this work, it is important to highlight that we have only considered two resource allocation profiles. Therefore, Q= {1,2} (i.e.,│Q│=2). Thus, for every incoming session served by the MC (i.e., either new or handoff), only one sub-subchannel with bandwidth fw will be allocated for the user. On the other hand, in the case of any type of sessions hosted by SCs, one or two sub-channels can be allocated.
3.3. User distribution
In this work, the MC is assumed to be located at the center of the HetNet coverage zone, whereas, the set of SCs are placed according to a repulsive point process. All this with the aim to guarantee that the SCs do not overlap each other. In this sense, a Matern Hard Core Point Process, denoted by Ф
SC
with density λ
SC
and a hard core parameter
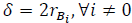 , governs the location of the SCs. As proposed in [3], we consider the users to be distributed in the coverage area according to the superposition of a Poisson Point Process (PPP) and a Poisson Cluster Process (PCP) [2]. For notation purposes, let Ф
ppp
u
represent the process of the uniformly distributed users in the coverage area, and
, governs the location of the SCs. As proposed in [3], we consider the users to be distributed in the coverage area according to the superposition of a Poisson Point Process (PPP) and a Poisson Cluster Process (PCP) [2]. For notation purposes, let Ф
ppp
u
represent the process of the uniformly distributed users in the coverage area, and
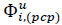 the i
th
set of users clustered around each SC, with densities represented by λ
ppp
u
and
the i
th
set of users clustered around each SC, with densities represented by λ
ppp
u
and
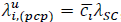 , respectively.
, respectively.
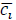 denotes the mean number of users in cluster i
th
. The overall Poisson process is hence
denotes the mean number of users in cluster i
th
. The overall Poisson process is hence
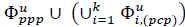 . As stated before, the users can be connected to either the MC or one of the SCs, and switch between them in a handoff process.
. As stated before, the users can be connected to either the MC or one of the SCs, and switch between them in a handoff process.
3.4. Traffic model
One of the most important issues when evaluating the performance of wireless network systems is the traffic model. We assumed that each possible event that can take place in the HetNet system arrives according to a Poisson process.
In general, the arrival rate of event 𝑒 is denoted by λ
e
, e Є E where E represents the set of events. In this way, two types of sessions can arrive to the system: new and handoff, and the corresponding mean rates are defined as follows: Let
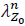 denote the arrival rate of new requests generated by users located in Z0, where all these petitions arrive to the system via the MC; ,
denote the arrival rate of new requests generated by users located in Z0, where all these petitions arrive to the system via the MC; ,
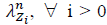 indicates the arrival rate of new session requests by users located in 𝑍 𝑖 , which are coming either via the MC (e.g., B0) or the i
th
SC (e.g., B
i
). On the other hand,
indicates the arrival rate of new session requests by users located in 𝑍 𝑖 , which are coming either via the MC (e.g., B0) or the i
th
SC (e.g., B
i
). On the other hand,
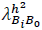 and
and
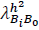 indicate the arrival of handoff petitions from ongoing sessions allocated in B
i
to B0 for each resource allocation profile defined, and
indicate the arrival of handoff petitions from ongoing sessions allocated in B
i
to B0 for each resource allocation profile defined, and
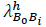 represents the arrival of handoff requests from ongoing sessions in B0 to B
i
. Due to the additive property of the Poisson process, the total arrival rate can be expressed as follows [10]:
represents the arrival of handoff requests from ongoing sessions in B0 to B
i
. Due to the additive property of the Poisson process, the total arrival rate can be expressed as follows [10]:
Lastly, the service rate assigned to every session in the system with only one sub-channel is denoted by µ. Thus, when 𝑞 sub-channels are assigned, the service rate will be qµ and the service time will be exponentially distributed with mean 1/qµ.
4.0 Radio access network selection and resource allocation strategy in two-tier HetNets
The RAN selection and sub-channel resource allocation processes in the downlink of the two-tier HetNet under co-channel deployment are cast as a sequential decision-making problem. In this scenario, particularly with regards to the decision-making process, when new incoming petitions arrive to the system, the RAN selection module must decide whether to accept or reject the request. If the session request is accepted, it is necessary to determine if it should be served either by the MC or any of the SCs, i.e. for those sessions that are being generated in zones with coverage from both types of RANs (MC or SCs). In addition to this, for those cases where the outcome of the decision process is that the new session should be allocated in one of the SCs, it is required to determine if one or two sub-channels can be assigned.
On the other hand, we would like to point out the fact that as a consequence of each session departure, the resulting state of the system can be further unbalanced. Therefore, in order to overcome the load imbalance situation as well as to alleviate the load in the MC, a load distribution process can take place at these points with the aim of distributing the traffic load over the set of RANs in a fair way. Hence, the system has the possibility to move a session from the MC to the any SC. The goal is to avoid a scenario with an overloaded MC and a set of underused SCs.
The above RAN selection and sub-channel resource allocation decision process is carried out taking into account the expected system reward, which is in turn computed in terms of the figurative revenue calculated by the income generated for the fair distribution of sessions between the MC and SCs minus the cost for the SINR level achieved at a specific instant of time. Likewise, the cost of power consumption of the two-tier HetNet system is considered to estimate the expected system reward.
Load metric: This work pursues the design of a load-based optimal policy for network selection process. Therefore, it is necessary to estimate the load of each RAN when new requests arrive. With regards to the specific load of each RAN, and given that each one has a specific capacity, the load of the MC cannot be directly compared to the load of the SCs. In this work, we consider the normalized load, which is defined by taking into account the number of users connected to a RAN at a specific time. Thus, to evaluate how resources are being used by each RAN, it is necessary to define a metric that allows us to determine the number of sessions allocated to each one. In the case of the MC, the normalized load is given by:
and for the SCs, it is defined as follows:
where 𝑠 denotes the number of ongoing sessions at a specific time (t) for RAN i th , and C indicates the maximum capacity of i th RAN in terms of the number of channels.
Fairness index: In our proposal, a main aspect in the process of the RAN selection, which has a direct impact on the load distribution, is the definition of an index that allows us to establish how fair the load distribution is between the MC and the SCs at time t. In order to evaluate the fairness level of load distribution among different RANs, we have employed Jain’s Fairness Index (JFI). This index is considered a quantitative measure of fairness, which was introduced in [11] and has been widely used and studied in the field of wireless networks [12]. JFI is defined as follows:
where γ ∈ [1/k+1,1] and k+1 denotes the number of RANs. In this work, the objective of the network access selection process is to receive the maximum possible reward and γ is increased when the decision is made.
Energy consumption model: Both types of base stations are powered by the on-grid energy supply and share the same energy cost per unit. Thus, we define the energy consumption model for the two-tier HetNet in terms of the consumption of the MC plus the consumption of the SCs as follows [13]:
where P B0 and P Bi represent the power consumption of the MC and SCs at time t, respectively. In general, the power consumption of the P Bi ∀ i≥0 , is calculated as follows [13]:
where Ps Bi denotes the fixed power consumption of the BS. On the other hand, ∆ Bi and P out Bi represent the dynamic portion of the total energy consumption. ∆ Bi is the slope of the load-dependent power consumption, P out Bi and P max Bi denote the power transmission and maximun power transmission of the i th base station, respectively.
SMDP problem formulation for RAN selection and resource allocation
In this section, we offer the description and details related to the SMDP RAN selection and resource allocation problem.
5.1. Discounted-reward SMDP model
The discounted reward SMDP model is defined by considering the following elements: i) decision-epochs, ii) states, iii) actions, iv) state dynamics, and v) reward.
1) Decision epoch: A decision epoch is defined as the time when an event occurs. In this way, all possible events are determined in terms of session arrival (i.e., new or handoff request) and session departure from the two-tier HetNet system. The system will be analyzed when either an arrival or a departure takes place. Since session arrivals are modeled as a Poisson process and the service time in the system is exponentially distributed, the time between two consecutive decision epochs will be governed by a random variable that follows an exponential distribution [3].
2) State space: The state space X is considered finite and defined by all possible states of the system. In this way, the system state of the two-tier HetNet at time 𝑡 is denoted by x(t) Є X, where x(t) is defined by the number of ongoing sessions allocated in each base station. Additionally, in the case of the SCs, the state of the system also reflects the number of sub-channels that are being used for a particular session at time t. The state also includes the variable e Є E , which denotes the current event taking place in the system. Therefore, the state space X is defined as follows:
Where s0 ≥=0, denotes the number of active sessions for the MC, and si 1 ≥=0 and si 2 ≥=0 denote the number of ongoing sessions that are using one or two sub-channels in the i th SC, respectively.
It is important to define the set of all possible events that can take place in the system. In this respect, let E represent the set of events in the HetNet system, which is defined as follows:
Where I={1}represents a new arriving petition in Z0, and L denotes the subset of events that represent new session arrivals via either the MC or i th SC in zones Zi∀ i>0 . 𝑇 indicates the subset of events representing a handoff operation from B0 to B1, and V 1 and V 2 represent the subset of events of handoff requests from B1 to B0 (i.e., V 1 and V 2 denote the subset for sessions with one and two sub-channels allocated in Bi, respectively). Finally, D denotes the subset of events that indicate a departure from Bi∀ i≥0. Particularly, for departure events in the SCs, it is important to mention that a departure event for sessions with one or two sub channels is considered. Thus, E can be expressed by:
According to the previous notation, each possible e ∈ E is going to take a value in the interval [ 1,6K+2) ] in order to specify the type of event.
3) Action: When an event takes place in the system, the decision entity has to make a decision with regards to which specific action to perform. In this context, it is necessary to introduce a finite set of actions. Let 𝐴 denote the actions for each possible state x = ( ŝ,e), where ŝ= ( s 0 ,s i 1 ,s i 2 ,…s 1 k ,s 2 k ), ∀ e Є E and i Є [1,k]. Three possible allowed actions have been identified for the RAN selection and resource allocation problem: continue, reject, and accept and allocate the event in the MC or i th SC.
Let A x be the set of possible actions available for each x Є X at each decision epoch time.
From eq. (14), we can observe that action α = 0 is available for all types of events, except for departures (i.e., e Є D), and it means that the incoming petition is rejected. For a departure, two types of actions are available, namely α = -1 and α = {K + 2,…,2k+1}. Action α = -1 means to continue, and indicates that one session abandons the system and nothing happens in the HetNet. On the other hand, if action α ={K + 2,…,2k+1} is selected, one session will abandon the system either from the MC or any of the SCs, and an offloading process will be carried out as long as there is the possibility to be performed (i.e. one session will be moved from the MC to ith SC). The offloading process is a network-based handoff, which allows moving an ongoing session from the MC to one of the SCs. If the event is accepted in the SC with action {K + 2,…,2k+1}, two sub-channels are allocated for the session selected to be moved. Action 𝑎=1 will be available for events related to the MC (i.e., e Є I,L,T,V1, V2,D), which means that there is a possibility for the decision entity to allocate the incoming session in the MC. When the decision-entity receives new session requests in zones Z j , ∀j>0 or handoff petitions from the MC to the i th SC (i.e., e Є T), the session can be either rejected with action α = 0 or accepted with action α ={2,…,K+1,K+2,…2K+1}
4) State dynamics: When an action α Є Ax is chosen in state x Є X, a transition happens from state x to state x’ with probability q(x│x’, α). As we can observe, the state dynamics of the system are determined by its transition probability matrix, which in turn depends on the action chosen by the decision entity in a particular state. Let 𝜏(x, α) be the sojourn time, which can be written as: 𝜏(x, α)= β(x, α)-1 where β(x, α) is the mean rate to leave state x, which is expressed in terms of the summation of the arrival and departure rates of all possible events in the state, and is given by:
The term 𝜂i is used to denote the proportion of ongoing sessions that could perform a handoff petition from B0 to Bi at a specific instant of time. As mentioned in section 3, we are assuming that the SCs are deployed where clusters of users are located, and therefore the parameter 𝜂i is calculated as follows:
In eq. (16), the operator 𝕀 represents the indicator function that equals one if the condition 𝜂is0 ≥1 is satisfied, and zero otherwise. Thus, in state x Є X, the handoff rate of sessions from B0 to Bi is taken into account, as long as the possibility of performing a handoff exists. Once the mean rate of the events for the two-tier HetNet system has been defined, we can proceed to estimate the transition probability matrix of the system. In this sense, let q (x’│x, α) denote the probability that in the next decision epoch, the system will be in state x’ considering that the current state is x and action 𝑎 is chosen. In the following, we describe how the transition probabilities q (x’│x, α) are computed for each possible state x Є X. For example, if the system is in state x Є X , (e.g., e Є I ) two actions are available, namely α=0 and α=1. If α=1 is chosen, the session request is accepted and the transition probabilities are given by eq (17). The other transition probabilities are calculated in a similar manner.
Reward: The main intention of the decision-making process is to maximize the total reward of the system. The reward function r(x, α) is defined in terms of the total reward received when the system is in state x Є X and action α Є Ax is selected. Taking this into account, the reward function is computed in the following way:
Where f(x, α) is the lump sum income received by the decision entity when action α has been chosen in state x Є X. On the other hand, c(x, α) denotes the system cost function for allocating a session over any RAN that belongs to the system. The income f(x, α) is defined as follows:
Where 𝑚 represents a figurative income (i.e.,$/Υ) received by the level of fairness of the system in state x. This value is established by the MNO according to its objectives and preferences. The fairness is calculated using eq. (7). In the same way, 𝑛 denotes the figurative cost for the level of aggregated SINR of the system in state 𝑥 (i.e., $/Γ).
From eq. (17), if a new or a handoff request is accepted with action α= {k +2,…2k + 1} to be hosted by one of the available SCs, the system will earn an income. If the session is rejected, however, there is no income associated. Likewise, there is no income for a session departure when the action chosen is a = 1. In addition, c ( x, α) is given by:
Where c ( x, α) is defined in terms of the energy consumption of the system at a specific instant of time. As we can observe, the energy consumption is multiplied by y as well as 𝜏(x, α), which denote the figurative cost for the power consumption (i.e., [$/ kW]) and the time between decision epochs, respectively. With regards to a session departure, the offloading operation has an associated cost defined in terms of the power consumption level in state x at time t. Hence, the total discounted-reward for the SMDP HetNet model is given by [4]:
Where β ( x, α) represents the rate and α denotes the discount factor.
6. Optimization problem
Assuming that the initial state of the system is x 0 , and if the network-controller follows the policy p, the expected discounted reward can be calculated by:
Where α denotes the discount factor, and r( x t , α t ) represents the reward earned in state x when action α is selected at time t.
The discounted reward is a well-known optimization performance criterion that has been widely used in SMDP problems [4]. The main goal of our work is to find a stationary deterministic optimal policy p to obtain the best state-action mapping (i.e., p: X ⟵A x ) with the aim of maximizing the total expected discounted reward. The optimal policy p can be obtained by solving Bellman equation:
In order to find an optimal policy p, we use the VI algorithm for solving the RAN selection SMDP-based model. Since these methods are designed to work in discrete-time, it is necessary to apply a uniformization process in order to obtain the equivalent SMDP model [4]. To achieve this, a constant transition rate is required. Thus, let 𝑐 be the parameter that indicates a fixed transition rate in the equivalent discrete-time model [4], which is defined as max β (x, α). The uniformization process [4] is hence defined as follows:
Where α represents the discount factor, and
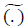 denotes the discrete-time equivalent. Once the uniformization has been carried out, the value iteration algorithm can be used to estimate the optimal policy. The pseudo-algorithm used to solve the SMDP optimization model is found in [4].
denotes the discrete-time equivalent. Once the uniformization has been carried out, the value iteration algorithm can be used to estimate the optimal policy. The pseudo-algorithm used to solve the SMDP optimization model is found in [4].
7. Performance metrics
With the aim of evaluating the effectiveness of the proposed approach, it is necessary to define the appropriate performance metrics. The embedded Markov chain of the optimal policy p can be used to obtain the steady-state probabilities ∏x for each state x Є X the corresponding performance metrics. In the following, we will define the performance metrics used in this article.
a) Blocking Probability: Based on the steady-state probability for each state ∏x, let P be represent the blocking probability for event e Є E which is given by:
b) Average Blocking Probability (ABP): In the scope of this article, and taking into account the blocking probability per event P be , we define the average blocking probability (ABP) of the system as follows:
c) Utilization: In the scope of this work, it is important to know how the RANs are being used for the proposed scheme. To this aim, the level of utilization of each RAN is given by:
d) Average Power Consumption: Taking into account the load of the system, it is possible to estimate the energy consumption in each state x Є X. Then, considering the steady state probability, we can determine the average power consumption, which can be written as:
7. Numerical results
In this section, we present the numerical results taking into account the set of metrics defined in the previous section.
7.1. System parameters and setup
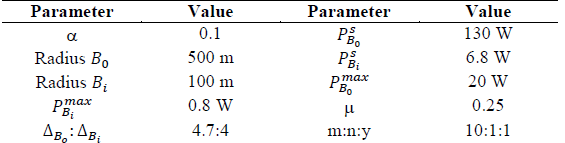
We considered a simple but a representative model of the downlink for the two-tier HetNet scenario under co-channel and user-centric deployment. We assume that one single MC cell located at origin coexists with two SCs, which are deployed by the MNO under the coverage area of the MC. The radius of the MC is set as rB0 = 500m and the same parameter for each SC is defined as r Bi = 100m.
In addition, we consider 500 users, which are distributed in the entire coverage area. The total available bandwidth is established as C = 10Mhz, and the bandwidth of each sub-channel is set as f w = 1Mhz. The AWGN σ2 is set to 1X 10 -13 W. The average channel gains are considered fixed for every sub-channel allocated to the MC or SC. G u,i = d -z u,i where d u,i is the average distance between an average user served by the 𝑖 𝑡ℎ base station, and z is the path loss factor, which is set to 2 for performance evaluation purposes. Also, we are assuming a maximum Offered Traffic Load (OTL) of 23.5 erlangs to evaluate the performance of the obtained policy, where an ABP around of 2% is expected.
In addition, with the aim of computing the parameter 𝜂, our experimental system setup is a circular area A = A
B0
= ∏r
2
B0
with a density of SC determined by λ
sc
= 2.54SC /Km2. The density of the uniformly distributed users in the A
B0
is λ
u
ppp
= 2 x 10-4
u/m2, and the density of users grouped around each SC is
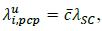 , where the average number of users per cluster 𝑐̅ = 100 for each cluster is established (i.e., since two SCs are deployed, there are two clusters). Table 1 summarizes the list of parameters used in the numerical analysis.
, where the average number of users per cluster 𝑐̅ = 100 for each cluster is established (i.e., since two SCs are deployed, there are two clusters). Table 1 summarizes the list of parameters used in the numerical analysis.
7.2. Performance evaluation
In this subsection, we evaluate the efficiency of the proposed policy in comparison to greedy (GREE) and random (RND) schemes. Due to the differences in terms of the modeling assumptions and the set of parameters used in previous and related works, it is not feasible to make a true comparison between these works and our proposal, therefore, we perform a comparison of our approach against RND and GREE strategies. RND will randomly select a RAN with uniform probability for those events in which the session can be allocated to the MC or one of the SCs. If the incoming event can only be allocated to the MC or an SC, this strategy will always accept the incoming petitions if there are available resources to allocate the session either in the MC or in an SC. On the other hand, GREE is defined as a myopic approach, which will select the RAN that allows getting the best reward at a specific instant of time, taking into account only local information for the decision process. Likewise, it will reject a session request only if there are no available resources.
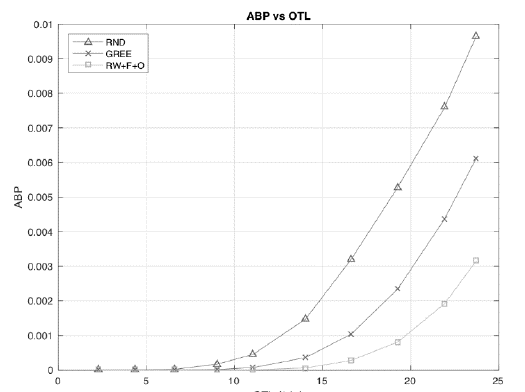
Fig. 1 shows the ABP as the volume of traffic in the system increases. For the three schemes considered, a higher ABP is expected as the OTL increases. Taking this fact into consideration, our strategy obtains a better system performance in terms of the ABP when compared to the RND and GREE approaches. The results indicate that the offloading process improves the ABP of the system in the long-term. In fact, numerical results show that a lower blocking probability is achieved when the offloading process is carried out.
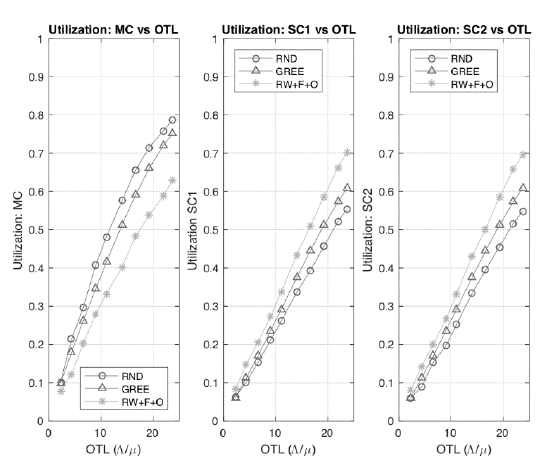
Fig. 2 shows that our SMDP-based approach results in a similar or lower radio resource use (i.e., sub-channels) of the MC in comparison to the SCs. Furthermore, the results show that the level of utilization of the MC obtained by the GREE and RND strategies is always higher than the utilization of the SCs.
Source: The authors.
Figure 2 Comparison of utilization of each RAN vs OTL for policies RW+F+O, GREE and RND.
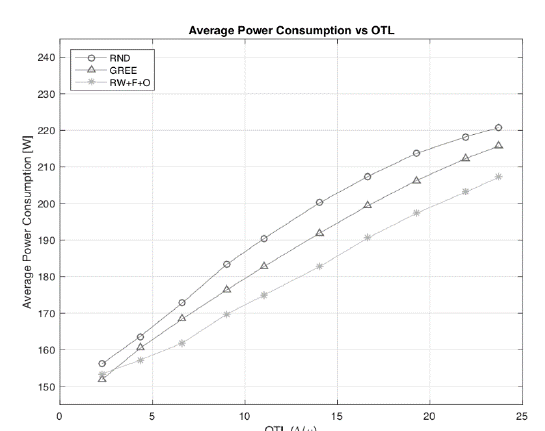
Fig. 3 shows the average power consumption of the two-tier HetNet by the three different strategies (i.e., RW+F+O, GREE, and RND). The results show that the energy consumption of the two-tier HetNet system increases with the traffic volume. This figure also shows that the RW+F+O scheme exhibits lower average power consumption than RND and GREE, in the long term. This is an expected result, since our policy achieves a lower utilization of the MC in comparison to the other two schemes.
Source: The authors.
Figure 3 Comparison of Average Power Consumption (APC) of HetNet vs OTL for policies RW+F+O, GREE and RND.
Also, since the MC consumes more energy than an SC, a lower utilization of the MC will contribute to reduce the overall power consumption of the system.
Conclusions
In this article, we studied the RAN selection, traffic offloading and resource allocation problem for the downlink of the two-tier HetNet under co-channel and user-centric deployment.
In this sense, we have proposed a discounted SMDP-based approach to address this problem, with the goal of maximizing the expected reward and enhancing the overall performance of the two-tier HetNet. These results in a fair use of radio resources by the set of RANs, which also leads to alleviate the level of use of the MC as well as a reduction of the energy consumption in the long term. The VI algorithm is used to solve the proposed model.
Numerical results have shown the effectiveness of the proposed strategy in comparison to greedy and random approaches.