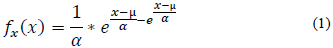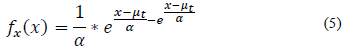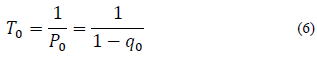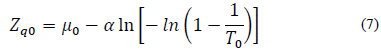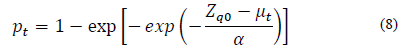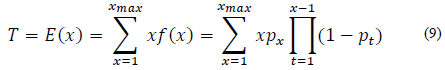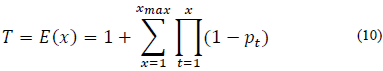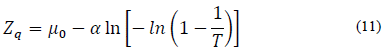1. Introducción
Las curvas de Intensidad-Duración-Frecuencia (IDF), representan una de las herramientas más utilizadas para estimar caudales máximos, que sirven para el diseño de obras hidráulicas y de infraestructura. Las IDF también son útiles en la estimación de tormentas de diseño, en sitios donde, debido a la falta de información de caudales es necesario recurrir a los modelos lluvia escorrentía para el cálculo de los caudales máximos.[1]
Actualmente las curvas IDF se estiman bajo un concepto estacionario, el cual considera que la precipitación permanece constante en el tiempo. Estudios recientes concluyen que en lugares dónde hay variabilidad climática es prudente construirlas bajo un enfoque no estacionario, para no incurrir en una subestimación de los eventos extremos de la precipitación y evitar así el colapso de obras hidráulicas y de infraestructura antes del periodo de vida útil de la obra.
La intervención humana es una de las principales causas de los cambios en el ciclo hidrológico de las cuencas hidrográficas, registros de precipitación y caudales pueden estar cambiando debido al efecto de los cambios en el uso de la tierra en las cuencas y debido al aumento de los gases de efecto invernadero en la atmósfera[2].
Además, se ha planteado que algunos de los cambios que los investigadores pueden estar observando en registros hidrológicos pueden deberse al efecto de la variabilidad climática natural, particularmente debido a los componentes de baja frecuencia de la variabilidad climática como la Oscilación del Sur de El Niño (ENSO) y las oscilaciones decenales y multidecales tales como la Oscilación Decadal del Pacífico (PDO) y la Oscilación Multidecadal Atlántica (AMO) [3].
El departamento de Antioquia se caracteriza por tener una alta variabilidad climática, éste se encuentra en medio de la región Andina, la cual desde el punto de vista de la subdivisión climática realizada por Snow (1976), pertenece a la categoría de clima montañoso. En esta zona se presentan situaciones extremas en cuanto al comportamiento de las precipitaciones se refiere, ya que están influenciadas en gran parte por la topografía [1,4].
En este estudio se estimarán las curvas IDF estacionarias y las no estacionarias para algunas de las estaciones dispuestas sobre la cuenca del río Medellín, se hará además una comparación entre ambos enfoques para tener un estimativo del error en el que se incurre al suponer que la precipitación tiene una tendencia a permanecer constante en el tiempo. La metodología y los resultados serán expuestos a lo largo del artículo, al final se presentarán unas recomendaciones para futuras investigaciones sobre el tema.
2. Metodología
2.1. Análisis de homogeneidad de la precipitación
Este análisis se realizará con el fin de evaluar la calidad de la información, a través de la detección de cambios en la media, varianza y tendencia de las series de tiempo, en este caso en la intensidad de la precipitación máxima anual de las duraciones seleccionadas (30, 45, 60, 75, 90, 105, 120 minutos).
Se dice que una serie es estadísticamente homogénea o estacionaria, cuando sus datos provienen de la misma población. De forma práctica, una serie hidrológica se considerará homogénea cuando tenga una sola media y una sola varianza[5].
En el análisis, se hará uso de pruebas no-paramétricas, para un nivel de significancia del 5%:
2.1.1. Detección de tendencia en la media
Una serie presenta tendencia en la media, cuando se da un cambio progresivo y gradual en la magnitud o el nivel de determinada variable[5].
Para detectar la existencia de tendencia en la media, se hará uso del test de Mann-Kendall.
Test de Mann-Kendall
La aplicación del test devuelve dos parámetros que sirven para determinar la existencia, o no, de tendencias en las series (estadístico τ) y su grado de significación estadística (α). Un τ = 0 indica la inexistencia de tendencia, mientras que conforme se aleje de 0 y se aproxime a 1 indica que existe una tendencia, bien sea positiva o negativa, dependiendo del signo de la misma[5].
La hipótesis nula Ho (indica que no hay una tendencia en la serie) es rechazada si el valor de p calculado es menor al nivel de significación alpha, tras la detección de una tendencia significativa, el parámetro de ubicación se calcula entonces bajo el enfoque no estacionario[2].
2.1.2. Cambio en la varianza
Se dice que una serie de tiempo presenta cambio en la varianza cuando se observa un cambio abrupto en el nivel o la magnitud de la varianza de determinada variable. En general estas pruebas evalúan la hipótesis nula de igualdad de varianzas entre las dos subseries resultantes de dividir la serie original por un punto de cambio[5].
Para detectar cambio en la varianza se hará uso de la prueba F modificada.
- Prueba F modificada
Esta prueba busca detectar cambios en la varianza cuando la muestra de la serie tiene una estructura de dependencia. Se asume que la serie de precipitación puede ser dividida en dos subseries y se deberá definir para cada una, el tamaño muestral equivalente [5,6].
La aceptación o rechazo de la hipótesis nula (Ho: No hay cambio en la varianza) radica en que el p calculado debe ser mayor que el nivel de significancia establecido (0.05) para que se acepte la hipótesis.
Tras la detección de cambio en la varianza, el parámetro de ubicación se calcula bajo el enfoque no estacionario.
2.1.3. Cambio en la media
Se puede determinar si la serie de precipitación es estable en la media a partir de la comparación de subconjuntos de la información. En la mayoría de las ocasiones se recomienda dividir la serie original en dos partes, de tal forma que se puedan aplicar test estadísticos de comparación de medias para determinar si vienen de la misma población[6].
Para detectar cambio en la media se hará uso de la prueba de Wilcoxon.
- Prueba de Wilcoxon
Se tiene una serie hidrológica, que se divide en dos subseries (antes y después del punto de cambio propuesto) y se quiere detectar si hay algún cambio en la serie después de dicho punto[6].
La hipótesis nula (Ho: las medias de ambas subseries son iguales) podrá ser rechazada si el p calculado es menor que el nivel de significancia establecido (0.05) y entonces el parámetro de ubicación se deberá calcular con el enfoque no estacionario.
2.2. Ajuste de la distribución de valores extremos tipo I (Gumbel)
La distribución más frecuentemente utilizada con series de máximos anuales es la distribución de valores extremos tipo 1 (EV1), también conocida como Gumbel, ésta es del tipo doble exponencial y su función de densidad de probabilidad está dada por[7]:
Dónde:
µ: Parámetro de localización
α: Parámetro de escala
2.2.1. Estimación de parámetros
Para la estimación de parámetros existen diferentes métodos en la literatura, entre los que se encuentran: método de los momentos, método de máxima verosimilitud, inferencia bayesiana y L-momentos.
Para este estudio se optará por el método de los L-momentos para hallar los parámetros en condición estacionaria y se usaran ventanas móviles para calcular los no estacionarios.
- L-momentos
Este método se ha propuesto como sustituto de los momentos ordinarios, sobre todo para trabajar con eventos extremos, ya que estos son mucho más fiables, al no verse afectados por la existencia de elementos extremos en la muestra. Los L-momentos son combinaciones lineales de los momentos ponderados por probabilidad (PWM) [7].
La estimación de los parámetros para la distribución Gumbel, resulta en las siguientes expresiones:
- Parámetro de escala α:
Dónde; s es la desviación estándar de la muestra.
- Parámetro de localización u 0
Dónde:
α: Parámetro de escala
Método de las ventanas móviles
El método de las ventanas móviles consiste en una ventana de tiempo de longitud fija que se desplaza con tamaño de paso constaste a lo largo de una serie de tiempo. Para el cálculo de los parámetros se puede emplear cualquier otra técnica, en este estudio por facilidad se empleará el método de los L-Momentos. Los resultados de este método dependen de tres factores, la longitud de la serie, la longitud de la ventana y el paso de tiempo[8].
De acuerdo con la metodología de Salas[3], cuando se considera la distribución no estacionaria, el parámetro de localización de la eq. (1), se calcula como sigue:
Dónde:
µ 0: Parámetro de localización estacionario
α: tasa de cambio anual del parámetro
t: tiempo
Como se puede observar “α” no es más que la pendiente de la línea de tendencia de la dispersión µ t vs t, vs t, esta tasa de cambio podrá ser positiva o negativa, si es positiva la ecuación se escribe con signo (+) y si es negativa con signo (-).
µt Se obtiene por medio de ventanas móviles, estableciendo un tamaño de paso ∆t y con µ 0 calculado previamente con el método de los L-momentos, resultaran entonces tantos µ t como ventanas móviles se tengan.
La función de densidad de probabilidad de la distribución Gumbel, queda como sigue:
2.3. Estimación no estacionaria del periodo de retorno con la metodología de Salas
Para el enfoque no estacionario, se debe rechazar la suposición de considerar variables aleatorias idénticamente distribuidas, por lo tanto año tras año la función de probabilidad no permanecerá constante[9].
Para condiciones no estacionarias el conjunto paramétrico varía con el tiempo, además, se asume que para el año inicial de la vida útil de una obra civil se ha llevado a cabo un estudio con base en un umbral de diseño Z q0 que corresponde al período de retorno T 0 [3]
Donde P 0 es la probabilidad de excedencia y q 0 es la probabilidad de no excedencia de Z q0 .
El cuantil de diseño en el momento t = 0 está dado por la expresión:
Dónde los parámetros µ 0 y α fueron hallados haciendo uso de las eq. (2) -(3).
La expresión de la probabilidad de excedencia variable con el tiempo, p t, en relación con el cuantil de diseño Z q0 se muestra a continuación:
Finalmente, a través de la eq. (8) se define el nuevo concepto no estacionario para el periodo de retorno.
Simplificada por Cooley (2003) como:
2.4. Estimación de curvas Intensidad-Frecuencia- Duración (IDF)
La metodología tradicional usada para el cálculo de las curvas IDF consiste básicamente en realizar un análisis de frecuencia a cada una de las series de valores máximos de precipitación obtenidos para cada duración[1].
Para calcular la precipitación máxima para cada periodo de retorno estacionario y para cada duración, se hará uso de la distribución EV1 (Gumbel), a partir de la eq. (7), dónde Z q0 corresponde a la intensidad máxima y T 0 corresponde al periodo de retorno estacionario.
Para la estimación de las curvas IDF no estacionarias se hará uso del periodo de retorno no estacionario T obtenido por medio de la metodología de Salas [3] descrita anteriormente.
Dónde Z q corresponde a la intensidad máxima con el enfoque no estacionario, α y µ 0 son los parámetros de escala y localización, respectivamente, calculados mediante el método de L-momentos y T corresponde al periodo de retorno no estacionario.
Finalmente, para graficar las curvas IDF se ubican la intensidad máxima hallada con la eq. (7) para el enfoque estacionario y con la eq. (11) para el enfoque no estacionario en el eje de las ordenadas y la duración en el eje de las abscisas.
3. Zona de estudio y datos
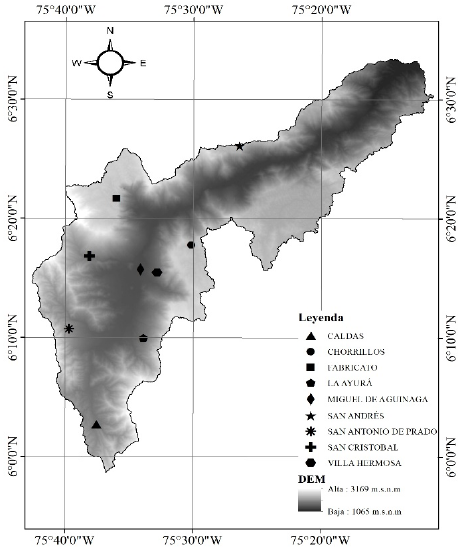
Para el desarrollo de este estudio se hizo uso de las series históricas de los eventos de precipitación de 9 estaciones pluviográficas ubicadas en la cuenca del río Medellín, ver Fig. 1.
Fuente: Los autores.
Figura 1 Cuenca hidrográfica del río Medellín y localización de las estaciones pluviográficas utilizadas.
En la Tabla 1, se relacionan las estaciones pluviográficas con sus respectivas longitudes de registro y el municipio en el que están ubicadas.
4. Resultados y discusión
4.1. Análisis de homogeneidad de la precipitación
En la Tabla 2 se presenta un resumen de los resultados que arrojó el test de Mann Kendall para las duraciones seleccionadas en cada una de las 9 estaciones.
Tabla 2 Resultados test de Mann Kendall para las duraciones seleccionadas en las 9 estaciones de estudio.
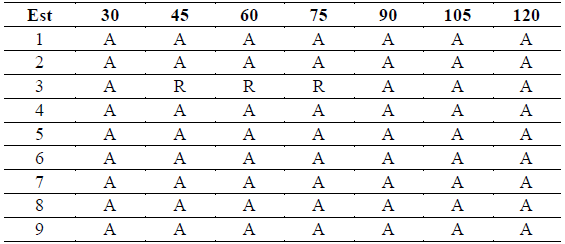
A: Acepta serie sin tendencia en la media
R: Rechaza serie sin tendencia en la media
Fuente. Los autores.
A continuación, se muestra en las Tablas 3 y 4 un resumen de los resultados de las pruebas aplicadas para determinar el cambio en la media y la varianza.
Tabla 3 Resultados Prueba F modificada para las duraciones seleccionadas en las 9 estaciones de estudio.
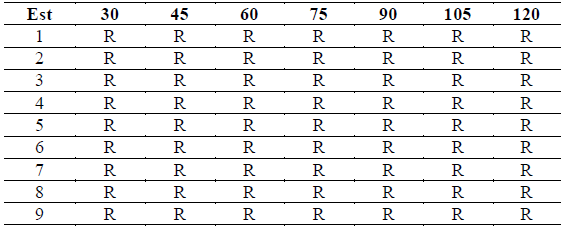
A: Acepta varianza estacionaria
R: Rechaza varianza estacionaria
Fuente. Los autores.
Tabla 4 Resultados Prueba de Wilcoxon para las duraciones seleccionadas en las 9 estaciones de estudio.

A: Acepta media estacionaria
R: Rechaza media estacionaria
Fuente. Los autores.
Los valores de τ para todas las estaciones dieron cercanos a 0 por lo que se concluye que no hay una tendencia significativa en la serie, el test de Mann Kendall no pudo rechazar la hipótesis nula H0 (indica que no hay una tendencia en la serie) ya que el valor de p calculado es mayor al nivel de significancia alpha (0.05).
La prueba de Wilcoxon arrojó que para las estaciones Caldas, Chorrillos y San Antonio hay un cambio en la media a diferencia de las otras 6 estaciones, en donde no se pudo rechazar la hipótesis nula Ho (las medias de ambas subseries son iguales), ya que, el valor p calculado es mayor que el nivel de significancia establecido.
En todas las estaciones y para todas las duraciones, la prueba F modificada arrojó un cambio en la varianza, lo que implica que las series de precipitación no son estacionarias y por lo tanto son válidas para el desarrollo de la investigación.
4.2. Estimación no estacionaria del periodo de retorno con la metodología de Salas
La Fig. 2 muestra la variación de T como una función de T0 para las 9 estaciones pluviográficas de la cuenca del río Medellín, T corresponde al periodo de retorno para el caso no estacionario, que fue calculado haciendo uso de la eq. (10) y T0 es el periodo de retorno inicial (caso estacionario).
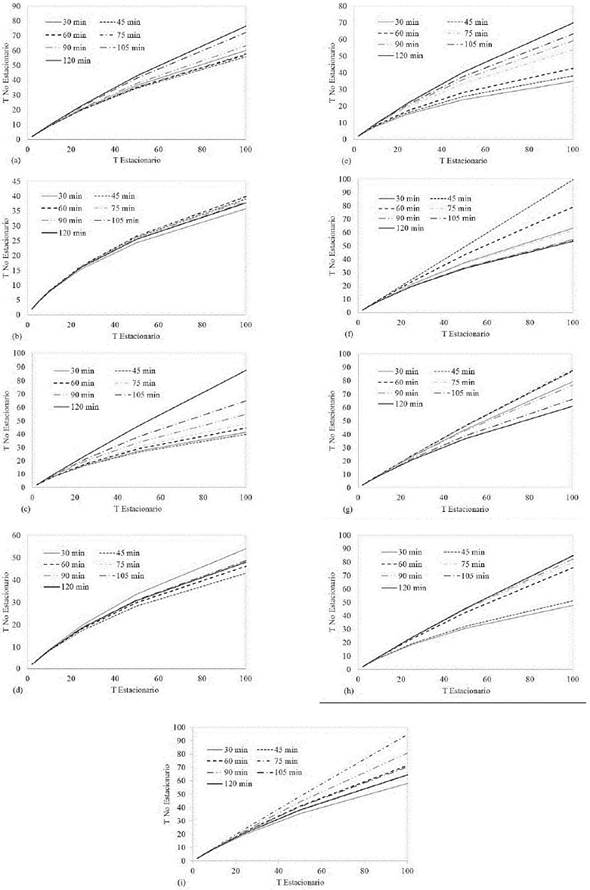
Fuente: Elaboración propia.
Figura 2 T Estacionario vs T No Estacionario para diferentes duraciones: (a) Caldas; (b) Chorrillos; (c) Fabricato; (d) La Ayurá; (e) Miguel de Aguinaga; (f) San Andrés; (g) San Antonio; (h) San Cristóbal; (i) Villa Hermosa.
De estas gráficas se puede observar que, para las 9 estaciones, el periodo de retorno no estacionario es menor que el periodo de retorno estacionario T0; por ejemplo, para las estaciones Caldas, Miguel de Aguinaga y Alto de San Andrés, para T0 igual a 100 años y una duración de 30 minutos, el periodo de retorno no estacionario es de 59.98 años, 34.8 años y 58.04 años, respectivamente.
Lo anterior significa que las obras deberán diseñarse con un periodo de retorno inicial mayor, al que se debe garantizar para su protección, durante la vida útil.
4.3. Estimación de curvas Intensidad-Frecuencia- Duración (IDF)
Se estimaron las curvas IDF tanto estacionarias como no-estacionarias para cada una de las 9 estaciones y para los diferentes periodos de retorno (2, 25 y 100 años) empleando el método de los L-momentos y el método de las ventanas móviles, ver Fig. 3.
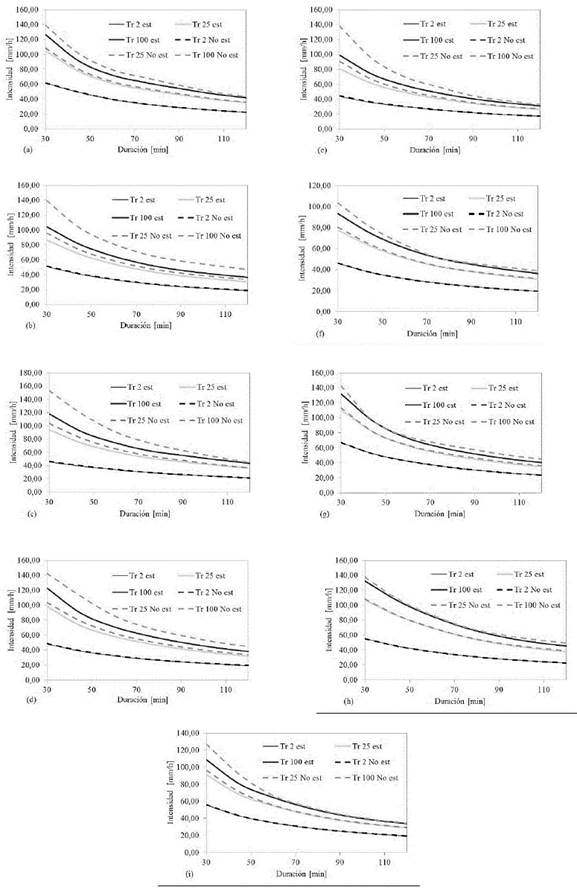
Figura 3 Curvas IDF Estacionarias vs No Estacionarias para diferentes periodos de retorno y duraciones: (a) Caldas; (b) Chorrillos; (c) Fabricato; (d) La Ayurá; (e) Miguel de Aguinaga; (f) San Andrés; (g) San Antonio; (h) San Cristóbal; (i) Villa Hermosa.
Haciendo uso de la metodología de Salas [3] se calculó también, el periodo de retorno bajo condiciones no estacionarias, necesario para que el diseño corresponda al periodo de retorno inicial T0 con el que se debe proyectar la obra, que en todos los casos es mayor, debido a lo que se explicó en el apartado anterior. Por ejemplo, para las estaciones Caldas, Miguel de Aguinaga y Alto de San Andrés, para T0 igual a 100 años y una duración de 30 minutos, éste periodo de retorno, es de 227.3 años, 1976.6 años y 246.29 años, respectivamente.
En la Fig. 3 El periodo de retorno usado para calcular la intensidad de la precipitación máxima en condiciones no estacionarias es el necesario para garantizar el periodo de retorno inicial T0, descrito en el párrafo anterior.
Se evidencia que la suposición estacionaria puede subestimar sustancialmente eventos extremos, por ejemplo, en la estación Miguel de Aguinaga para un periodo de retorno de 2 años y una duración de 30 min, la diferencia entre la no- estacionariedad (44,60 mm/hr) y estacionariedad (43,60 mm/hr) de precipitaciones extremas es de aproximadamente 1.00 mm/hr (2.3%), mientras que, para un periodo de retorno de 100 años para la misma duración, la diferencia entre no estacionariedad (138,12 mm/hr) y estacionariedad (99.01 mm/hr) es de 39.11 mm/hr (39.5%). De lo anterior se evidencia que mientras mayor sea el periodo de retorno, mayor será el porcentaje de cambio entre ambos enfoques, se puede notar además que, el cambio es más apreciable para duraciones pequeñas, aproximadamente hasta los 50 min.
5. Conclusiones y recomendaciones
Una suposición estacionaria subestima el pico de crecida y como resultado, el riesgo de inundación real será mayor al con el que el sistema o infraestructura había sido diseñado, esto significa que obras que han sido diseñadas para un periodo de retorno de 100 años, fácilmente podrían llegar al final de su vida útil en un periodo de retorno mucho menor.
Las 9 estaciones presentaron un comportamiento muy similar, para duraciones menores a 50 min se ve más marcada la no-estacionariedad y de 50 min en adelante, el porcentaje de cambio empieza a ser menos apreciable; se puede decir entonces que este enfoque funciona muy bien en cuencas pequeñas, dónde las duraciones son también pequeñas.
Como complemento a éste estudio podría incorporarse la metodología de Salas[3], dada la utilidad del análisis no estacionario para hacer una evaluación del riesgo de una estructura hidráulica durante la vida proyectada de la obra.
Para un trabajo posterior, otro complemento podría ser hacer una selección de la función de distribución que más se ajuste a las series históricas, una buena opción sería a través del método gráfico de los L-momentos.
La distribución GEV también se utiliza mucho en hidrología para el ajuste de series máximas, una recomendación si se va a trabajar con esta distribución, es estimar los parámetros mediante el método de la máxima verosimilitud Generalizada (GML), ya que la resolución numérica de las ecuaciones de máxima verosimilitud puede conducir a problemas de convergencia y puede, en algunos casos; resultar en soluciones que no son físicamente aceptables. El método GML incorpora una distribución anterior para el parámetro de forma que elimina soluciones imposibles[10].