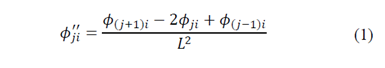1. Introduction
Modern structures, such as footbridges and grandstands, tend to be very flexible due to the increased resistance of new materials and the regulation gap in building codes. These flexible structures are susceptible to excessive vibrations induced by human activities, which can produce serviceability failures and, sometimes, collapse [1]. An example is the Millennium Bridge in England which presented excessive vibrations due to pedestrians, and led to the closure of the bridge [2]. In developing countries such as Colombia, numerous bridges have collapsed due to a variety of factors, including structural deficiencies and construction errors, and have caused significant social and economic impacts [3]. Hence, the early identification of incipient damage is important for timely decision making and to prevent catastrophic failures.
Visual identification of failures does not generally represent the current state of a structure [4]. For this reason, the field of structural monitoring has gained momentum and different methods of damage detection have been developed based on the dynamic properties of the structure [5]. These methods include techniques that use the basic modal forms and their correlation, as the MAC (Modal Assurance Criterion) and CoMAC (Coordinate Modal Assurance Criterion). These techniques have the disadvantage that the identification does not include damage location [6]. There are also methods based on derived structural parameters such as the mode shapes curvature [7,8], strain energies and methods based on the stiffness and flexibility matrices that allow identifying and locating the damage [9,10]. These parameters have also been used for a Differential Evolution stochastic method applied to the damage detection problem [11]. Other investigations have developed methodologies for damage detection using moving loads that simulate vehicular traffic on the bridge [12,13]. Some authors have implemented multi-criteria techniques in order to obtain more accurate results, including changes in frequency, flexibility and deformation energy [14]. In addition, more robust techniques for locating damage have been implemented, such as the design of damage detection filters using genetic algorithms [15] and techniques based on a machine learning approach using artificial neural networks [16,17].
The evaluation and comparison of different damage identification methods is of interest, as efficient and reliable methods are needed that can provide accurate information of the damage for preventive decision-making. This paper presents the numerical and experimental evaluation of three damage identification techniques in a full-scale footbridge: Damage Locating Vectors, Mode Shapes Curvature and Artificial Neural Networks.
2. Damage identification technique
2.1. Damage Locating Vectors (DLV)
The Damage Locating Vectors technique (DLV), developed by Bernal [18], is a procedure that allows the identification of a potentially damaged set of elements using the changes in the flexibility matrix of the structure. This technique identifies the elements from a set of vectors that induce zero stress on the elements that present damage. The potentially damaged elements are those having Weighted Stress Index (WSI), which represents the weighted average of the normalized stresses of the elements, less than one (WSI < 1). According to [19], the implementation of this technique can be summarized in the following four steps:
(i) Estimate the change in the flexibility matrix (DF).
(ii) Compute a singular value decomposition of matrix DF and the internal stresses in a health model of the structure using the eigenvectors as loads. Then, obtain a Singular Value Normalization index (svn) through the normalized product of the eigenvalues and the internal stresses, in order to choose the localization vectors. The vectors that have svn<0.2 can be treated as localization vectors.
(iii) Compute the Normalized Stress Index vector (nsi) for each localization vector.
(iv) Obtain the Weighted Stress Indices (WSI) for determining the potentially damaged elements. The elements with WSI<1 belong to the potentially damaged set.
2.2. Mode shapes curvature
The identification of damage using the mode shapes curvature is based on the fact that the region of the damage is located near the Degrees Of Freedom (DOF) that present changes in the curvature of the modes, due to reductions in flexural rigidity [20]. Thus, the absolute difference between the mode shapes curvature of the healthy and damaged structure will provide the region where the damage occurs. The mode shapes curvature
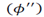 can be obtained numerically using the approximated central difference as [21]:
can be obtained numerically using the approximated central difference as [21]:
where
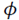 is the modal shape,
is the modal shape,
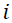 is the number of the modal shape,
is the number of the modal shape,
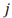 is the node number and
is the node number and
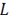 is the distance between the nodes. Finally, the absolute difference of the curvature
is the distance between the nodes. Finally, the absolute difference of the curvature
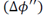 is calculated between the healthy state and a damaged state. In this paper, the curvatures in the reference structure were obtained in two directions (vertical and transverse) and the product of the curvatures was also calculated to provide additional information.
is calculated between the healthy state and a damaged state. In this paper, the curvatures in the reference structure were obtained in two directions (vertical and transverse) and the product of the curvatures was also calculated to provide additional information.
2.3. Artificial neural networks
An Artificial Neural Network (ANN) is a numerical model inspired in the human nervous system. Generally, ANN methods are trained such that a particular input leads to a specific output, and the network is adjusted based on a comparison between the output and the target until both match [22]. The input information for the ANN depends on the information available and the parameters required for the output. In this case, the selection and processing of the information for the network training can be generalized in the following steps:
- A random number of damage scenarios were simulated. For each scenario, a random number of elements per section on the bridge were chosen, then, it was randomly determined which elements would be eliminated to simulate damage.
- A finite element model was built for each simulated scenario and the acceleration response in the DOFs of the proposed sensor configuration were obtained. The model input consisted of white Gaussian noise, which was band-pass filtered between 0.5 and 30 Hz, and had a duration of five minutes.
-The acceleration responses of the models were transformed to the frequency domain using the output of one DOF as reference. The values in the transfer function corresponding to the first five natural frequencies of each model were selected, producing five vectors, each with 44 elements.
- Finally, the vectors corresponding to the first three frequencies were summed with the vector of the fifth frequency and used as the input for the ANN. The vector corresponding to the fourth frequency was not used due to difficulty in its identification.
The ANN consists of two layers that use the linear function and tan-sigmoid transfer function respectively. This last function outputs values between -1 and 1. The network indicates the presence of damage in a section where the output value is close to one. The output layer was designed with twelve neurons, such that the output information could identify damage in twelve possible sections of the bridge. The output is a vector with a value of 1 at the position where the damage occurs and zeros at all other positions. For real conditions, where the input vector includes the effects of noise, the elements of the vector are not exactly zeros and ones. The number of neurons for the hidden layer was increased from 5 neurons until satisfactory results were obtained.
3. Reference modal identification and damage scenarios
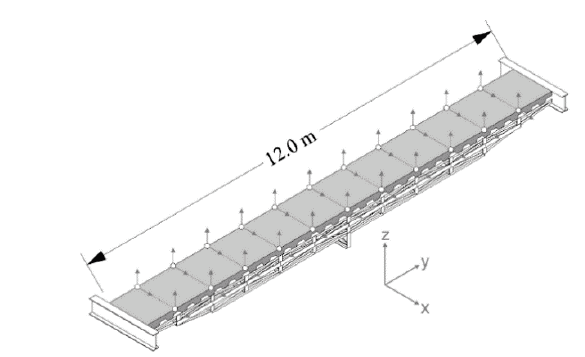
The structure used for this research is a footbridge that was custom built by the School of Civil Engineering and Geomatics of the Universidad del Valle for the study of human-structure interaction and damage identification (Fig. 1).
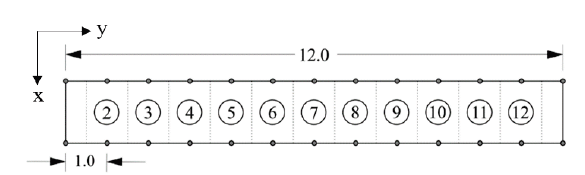
The footbridge, with a total length of 12 m and width of 1.2 m, was designed and built such that its structural configuration can be modified to achieve variations in its stiffness. For this purpose, a part of the truss structure has bolted connections and elements can be removed to generate different damage scenarios.
The dynamic properties of the footbridge were identified using the responses at 44 degrees of freedom (Fig. 2) to ambient vibration tests. Accelerations were measured with six seismic accelerometers, three included in a triaxial REF TEK model 130- SMA and three uniaxial REF TEK model 131B-01/1 sensors. Data acquisition was done at a sampling rate of 100 Hz. The identification of natural frequencies, damping ratios and mode shapes was performed using the Stochastic Subspace Identification method (SSI) [23]. Five natural frequencies (f) with Standard Deviations (SD) and modal shapes are shown in Fig. 3.
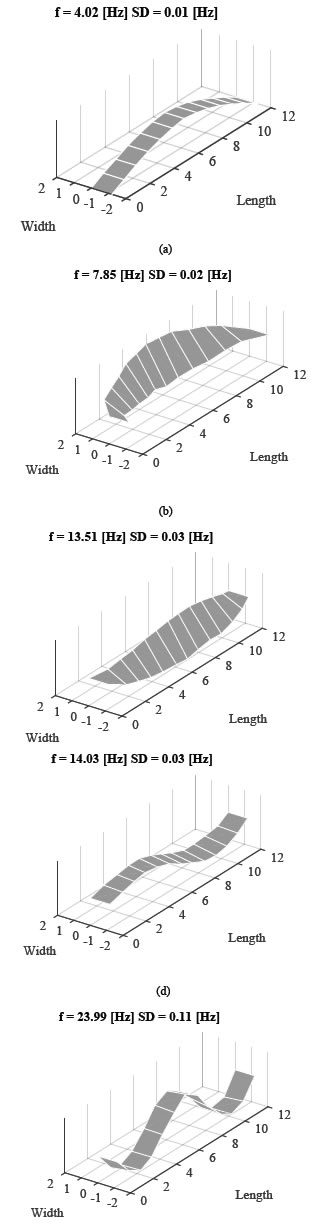
Source: The Authors.
Figure 3 Experimental mode shapes. (a) Mode 1; (b) Mode 2; (c) Mode 3; (d) Mode 4; (e) Mode 5.
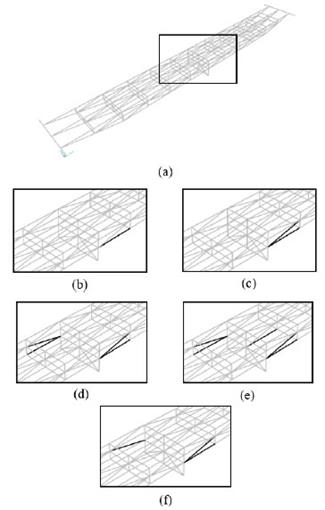
Five damage scenarios were defined, four of which were defined on the basis of the largest stress value criterion, and the fifth which was selected randomly (Fig. 4). For each damage scenario single elements were removed successively, for a total of five damaged elements in scenario five.
4. Numerical simulations
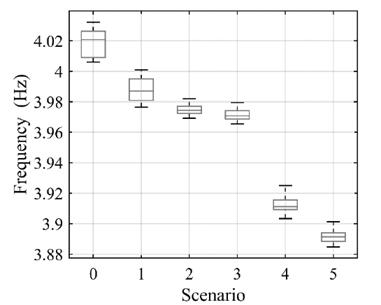
The footbridge was modelled with finite elements using SAP2000 and the model was updated using the experimental results. The Modal Assurance Criterion (MAC) was used for statistical data analysis as a quality indicator to measure the degree of consistency or linearity of the experimental mode shapes [24]. The fundamental natural frequency of the five models with damage scenarios differ to that of the undamaged model by 0.91%, 1.71%, 1.90%, 3.38% and 4.77%, respectively. The minimum and maximum differences in frequency between the numerical and the experimental results are 0.01% and 6.73%, respectively. The minimum and maximum MAC between the numerical and experimental values are 0.945 and 0.998, respectively.
4.1. Damage locating vectors: numerical simulations
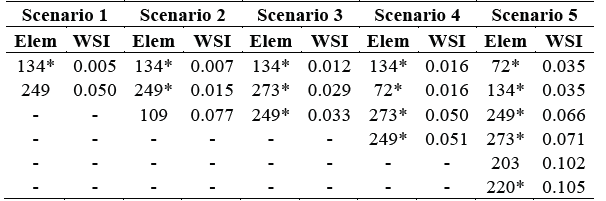
The five damage scenarios for the experimental validation were numerically evaluated using the DLV technique. The flexibility matrix was obtained through the application of unit forces and calculation of displacement [25]. Employing a threshold of WSI equal to 1.0, 65 potentially damaged elements were identified, which included the actually damaged elements. As the WSI index depends on the stress in the elements of the structure, those elements that have very low stresses under any load combination, are identified in the set of potentially damaged elements. Hence, in order to reduce the number of potentially damaged elements, the threshold of the WSI index was decreased to 0.1.
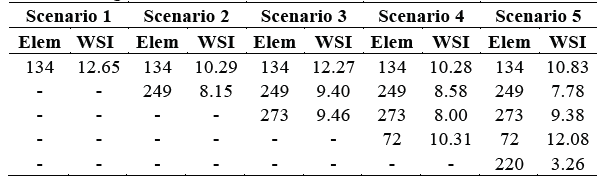
Using this value, it was possible to identify the damaged elements in the first four scenarios however, for the fifth scenario it was necessary to increase the threshold to 0.11. The number of potentially damaged elements and their corresponding WSI for each damage scenario are given in Table 1.
4.2. Mode shapes curvature: numerical simulations
The number of DOFs where the structural response is measured, limits the information the mode shapes curvature can provide. Hence, this method has the shortcoming that the identification of the location of damage in the bridge is limited to the general section that contains the damaged element. Simulations were performed considering 11 sections of the bridge and using 26 measurement points on the structure (Fig. 5). Information from two DOFs at each point (one horizontal and one vertical) was obtained and the five damage scenarios were simulated. Fig. 6 shows the differences in the mode shapes curvature between the healthy state and the five simulated damage scenarios. The damaged sections are identified in the first and second mode shapes for scenarios 1, 4 and 5. The largest variations occur in the second and fourth mode shapes for damage scenario 3, while variations were insignificant for damage scenario 2 due to the small amplitude of the changes.
Source: The Authors.
Figure 5 Sections and measurement points for the identification using mode shapes curvature.
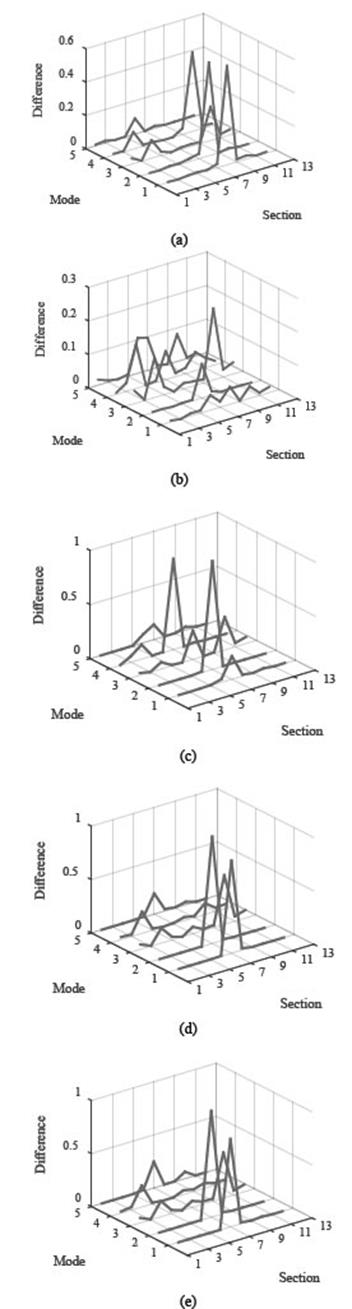
Source: The Authors.
Figure 6 Absolute differences between mode shapes curvature for the five proposed damage scenarios (simulations). (a) Scenario 1; (b) Scenario 2; (c) Scenario 3; (d) Scenario 4; (e) Scenario 5.
4.3. Artificial neural network: numerical simulations
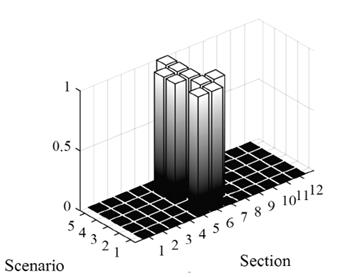
The ANN was used to identify damage in the 12 sections shown in Fig. 7. The five cases of damage were evaluated on the neural network, and a correct damage identification was successful for all scenarios. However, for the second scenario, section six was falsely identified as being damaged.
5. Experimental evaluation
The truss elements corresponding to the previously defined damage scenarios were physically removed from the structure. The test protocol used for the modal identification of the undamaged footbridge was also applied to the structure with each of the five damage scenarios. The differences in frequency associated to mode 1 between the healthy state and the five damage scenarios are: 0.77%, 1.09%, 1.18%, 2.64% and 3.17%, respectively. The variations of the first frequency for the five scenarios are shown in Fig. 8.
The MAC indicator was used to correlate the mode shapes for each of the damage scenarios with those of the undamaged structure. For all cases, the minimum value in the main diagonal is 0.98 and the maximum value off the main diagonal is 0.05. This implies that changes in the modal shapes are not significant and, hence, damage to the footbridge has a greater influence on natural frequencies.
5.1. Damage locating vectors: experimental evaluation
The experimental dynamic properties of the structure were used to calculate flexibility matrices for the damaged and undamaged cases based on the procedure proposed by Duan [26]. Using this information and evaluating the DLV technique for the five damage scenarios, at least 20 potentially damaged elements were identified for each cases. However, none of these elements corresponded to those that were actually removed.
Table 2 shows the values obtained for the WSI of the elements in which the damage was induced. For all five cases the WSI is greater than one and, hence, it is considered that for this case the method proposed by Duan [26] is not an appropriate method for calculating the proportional flexibility matrix.
5.2. Mode shapes curvature: experimental evaluation
Differences in the mode shapes curvatures were calculated with respect to the healthy state for each damage case. Fig. 9 shows the differences in curvature for the first five modes and the five damage scenarios. For the first scenario, the most representative change occurred in the fundamental mode.
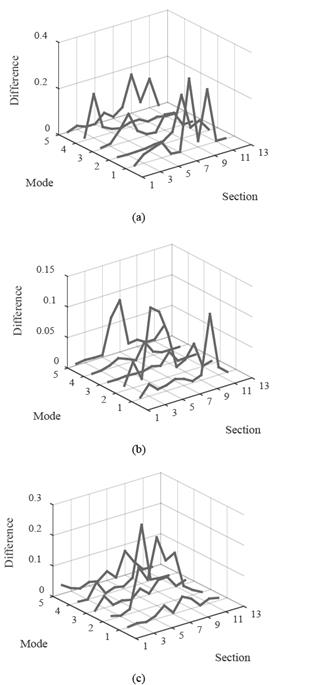
Source: The Authors.
Figure 9 Absolute difference between mode shapes curvature for the five damage scenarios (experimental): (a) Scenario 1; (b) Scenario 2; (c) Scenario 3; (d) Scenario 4; (e) Scenario 5.
However, the location of damage is not accurate, as there is one peak in the central section where damage is located, but also another peak in the adjacent section. For damage scenario 2, there is a significant difference of modes two and five in the section where damage was induced. For the following two scenarios, modes two and four have significant differences in the section where the damage was induced. Finally, for damage scenario 5, the difference in the mode curvature four corresponds to the section where damage occurs.
5.3. Artificial neural network: experimental evaluation
The same procedure as that described in Numerical Simulations, was applied to obtain the input vectors of the ANN for the experimental tests. This data was used to evaluate the performance of the ANN for the five damage scenarios, and the respective results are shown in Fig. 10. The ANN did identify the central sections as being potentially damaged, but section 5 was falsely identified as damaged in three of the scenarios. In the first scenario, the ANN falsely identified two sections as damaged, but in all of the other scenarios at least one section was correctly identified.
6. Conclusions
The results obtained from the numerical simulations of the DLV technique show that this technique can successfully locate damaged elements, as long as the threshold for the WSI is reduced. However, the experimental evaluation of the technique did not produce satisfactory results. It should be noted though, that it is likely that the technique used to estimate the proportional flexibility matrix was inadequate for this case.
For the case of numerical simulations, the technique based on the mode shapes curvature showed satisfactory results for four of the five damage scenarios, with correct damage localization. The experimental evaluation of this technique shows that some modes can have significant changes in the curvature at locations corresponding to the actual damaged sections. Although this technique proved to be a simple and fast alternative for the estimation of structural damage, it only allows a correct identification of the general area of damage. It is important to emphasize that this technique is computationally simple and does not require a numerical model.
The ANN was successful in correctly identifying the damaged sections for all cases of the numerical simulations. Only the case of the second damage scenario produced a false positive, with one section being incorrectly identified as damaged. For the case of experimental data, the ANN correctly identified the central section of the bridge as being damaged, however, in some cases some undamaged sections were falsely identified. Although ANNs can be an efficient technique for the detection of damage, they have the disadvantage that the development and training of the network is done based on the numerical model of a particular structure and, therefore, it is necessary to redesign the network and train it for each specific structure with a representative number of damage scenarios.