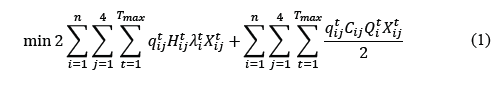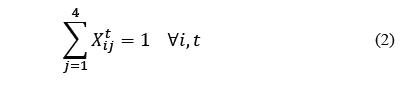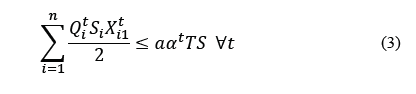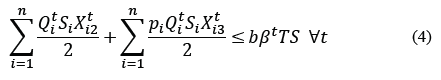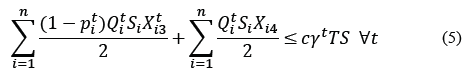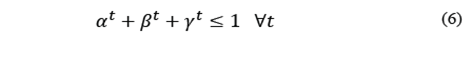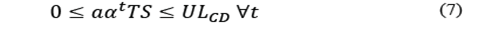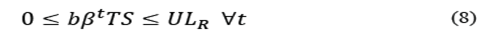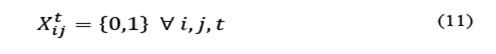1. Introduction

Today businesses evolve fast making it necessary for companies to compete in different aspects of globalization. According to Tompkins et al. [¹], around 20% and 50% of the total operating expenses in manufacturing companies are attributed to goods storage and handling. An efficient facility planning can reduce around 10% to 30% of those costs [¹,²]. In that way, facilities and operation design is a very important activity for which companies should develop sophisticated systems to ensure fast and effective responses to customers’ needs and permanent improvement of internal processes [³].

One important decision in facility and operation planning is the design and dynamic allocation of storage spaces, which can be done using mathematical techniques that establish the allocation of the different items in specific spaces into warehouses [¹]. The quadratic allocation method is used to model the allocation of the products, which consists in the assignment of a set of elements into a set of spaces when the distances between all locations and the flow of the products are known [⁴].

This article presents the application of a storage allocation model for five different types of products in a six-period time horizon in a Colombian company dedicated to the distribution and commercialization of food products. To do this, an optimization model and its solution algorithm are presented, which is in charge of defining the correct product allocation in the different areas of the warehouse in each period. The optimization model is developed and applied using GAMS © software. The article starts with a literature review about storage allocation models and methodologies, followed by the model formulation and the solution procedure. The data obtained from the company for the model application is later presented, to finally report the results and conclusions of the paper.

2. Literature review

According to some authors, there are few publications about the design of storage systems [⁵] and there is not a literature synthesis about those techniques [⁶]. This lack in the literature is evidenced by the absence of systematic procedures and the scope on a few particular aspects of the allocation design.

Kostrzewski [⁷] mentions that warehouse system planning can be classified into four types: design and distribution of storage space, order preparation, technology, and equipment selection for material handling and warehouse location. This work focuses on the first two activities. Behnamian & Eghtedari [⁸] characterized the allocation storage problem and verified different criteria for that. Within these applications, the multi-level warehouse layout problem is highlighted, from which various solution strategies have been explored, using metaheuristics techniques such as genetic algorithms [⁹,¹⁰], ant colony [¹¹], and tabu search [¹²]. Other authors have considered some restrictions such as operability [¹³], compatibility between products [¹⁴], replenishment policies [¹⁵], routes for order preparation [¹⁶], worker efficiency in order preparation [¹⁷] and technology usage [¹⁸]. Bottani et al. [¹⁹] consider the simultaneous storage allocation and the preparation of the orders through a metaheuristic based on genetic algorithms. Heragu et al. [²⁰] consider product allocation and the warehouse sizing through a heuristic based on a branch and bound algorithm.

Faber et al. [²¹] proposed the use of management indicators to evaluate the operational performance of storage systems. Roodbergen et al. [²²] proposed an inventory-policies analysis to determine the most appropriate warehouse design. Abdoli & Kara [²³] structured the warehouse elements and described five major processes: reception, storage, order preparation, product classification and order fulfillment. Adarme et al. [²⁴] evaluated the application of a warehouse design model in a shipyard trying to minimize the design, material handling and warehousing costs.

When using shelves, several possibilities can be considered to minimize movements through the aisles. Meller & Gue [²⁵] presented and characterized different aisle configurations in warehouses. Pohl et al. [²⁶] compared and qualified aisle configurations, highlighting the performance of the fishbone configuration. Cardona et al. [²⁷] also analyzed the fishbone configuration, highlighting optimization conditions for movements in warehouses.

One important aspect to be considered in warehouses is the possibility to store products without using shelves, which is known as block stacking. There are some models that can be used to minimize allocation activities when using this kind of warehousing [²⁸]. Buil & Piera [²⁹] applied dynamic programming to solve the reallocation problem in block stacking. Caserta et al. [³⁰] proposed a binary coding to quickly identify and assign the state of a space for block stacking. Kim & Hong [³¹] suggested two methods for block relocation: the first based on a branch and bound algorithm and the other using a heuristic procedure.

There are some recent literature reviews that can lead to a better understanding of the mentioned areas, such as the work of Gu et al. [³²], which focuses on warehouse design and operations evaluation, and the work of Da Cunha Reis [⁶], which reviews the issues of storage design, space allocation, routing and order preparation. Several metrics can be used to determine warehouse performance. Staudt [³³] made a literature review about warehouse performance metrics and showed the calculation technique for some indicators which were classified into four dimensions: cost, time, productivity and quality [³⁴].

3. Model formulation and solution procedure

The following model is developed to assign the amount of several products to be located in different areas inside warehouses, aimed to reduce both holding and material handling cost in a defined time horizon. Three typical operations areas were selected to be part of the model formulation: product reception, storage in reserve area and order preparation in the shipment area. This formulation is based in the works of [²⁰] and [³⁵], and the products are denoted by set I={1,2,…,n}, each having a material flow J={1,2,3,4}, which are: 1-Crossdocking flow, 2-warehouse operation flow in which only the products with long storage times are moved, 3- warehouse operation in which the products are kept in the reserve area and then moved to the shipping area until their requirement, 4- allowed crossdocking in the shipping area for very short storage times. The model assumes a dynamic behavior of the products making necessary the establishment of different policies in each period T={1,2,…, 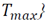according to the formulation proposed by [³⁶].

The objective function is presented in eq. 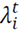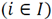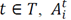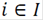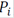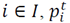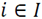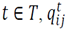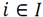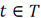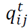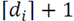(1), in which is the product demand in period ,is the ordering cost for product in period , , is the cost of every loaded unit of product is the percentage of the total time that every product requires to be assigned to flow 3 in period is an integer variable equal to 1 if product is assigned to material flow j=1, 2 or 4 in period ; if the product is assigned to flow j=3, is , in which 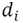is the size relation of the load unit in the reserve and the shipment area in period .

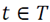a, b and c represent the percentage of the total available space for the operation areas: a-crossdocking, b-reserve and c-shipment. 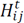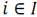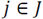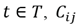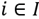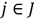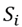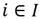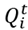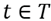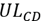is the holding cost of every single load of product associated to the material flow in period , is the material handling cost for a unit load of product with the material flow , is the required space to keep a unit of product , TS is the total warehouse space, is the amount of product ordered in period , is the maximum available space in the crossdocking area, 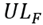is the maximum available space in the shipping area, and 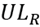is the maximum available space in the reserve area. The decision variables are 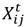, which is a binary variable equal to 1 if product belongs to material flow 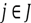in period 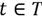or 0 otherwise. 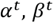and 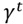are the assigned space for every area in the warehouse in period 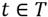, with 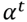-cross-docking assigned area, 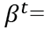reserve assigned area and 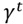=shipping assigned area.

subjected to,

Eq. (2) assures that only a single material flow is assigned to product i∈𝐼. Eq. (3) to (5) correspond to the available space restriction in period 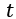. Eq. (6) assures that the space assigned to each area in every period is less or equal to the available space. Eq. (7) to (9) define the upper limit of space that can be assigned to each operation area, and Eq. (10) to (11) define the decision variables.

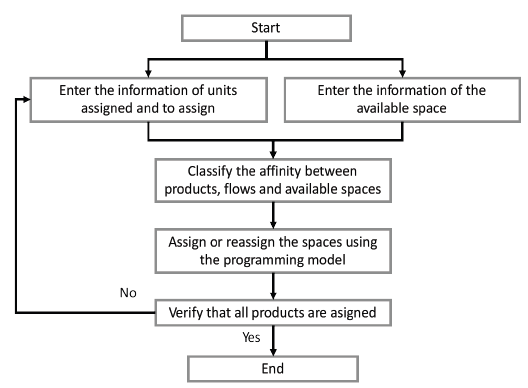
The following algorithm was proposed for the design and allocation of the areas required for the warehouse activities, which is composed of the steps presented in Fig. 1.

Source: The Authors.

Figure 1 Solution algorithm for the storage allocation problem. 

The algorithm starts with the acquisition of the operation information, mainly referring to product data and warehouse spaces. Afterward, the products are classified according to the flow required for each product inside the warehouse. This is determined mainly for the expiration date and the affinity requirements of every product. Then the storage allocation model presented above is used. After that, the costs are evaluated and verification of the assignment of all products has to be done. The algorithm finishes when all products are assigned.

4. Company description

The allocation problem in a Colombian food company was considered for the application of the model presented. The operation inside the company’ warehouse is complex since different products with different expiration dates have to be kept there. There are products that have to be kept for around six months, products with more prolonged storage time and other products with shorter warehousing requirements, generally due to their immediate consumption. This behavior is frequent in distribution centers of large companies that supply a large number of sales points on a daily basis, in the distribution of massive-consumption products and even in companies with models of shared warehouses [³⁷].

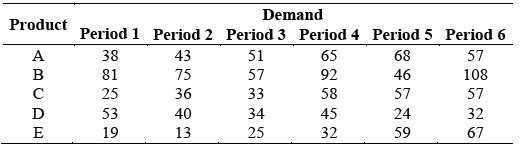
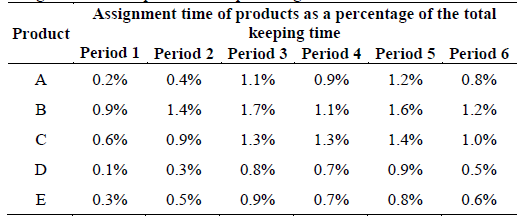
For the analysis, the five most important products due to their volume were selected for the storage allocation problem. The demand of every product in load units is showed in Table 1 for the time horizon of six periods.

Table 1 Product demand in units 

Source: The Authors.

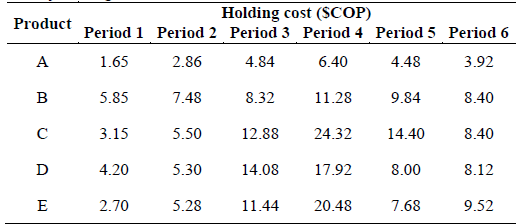
The total holding cost for each product in every period was calculated considering the corresponding costs of the storage space, public services, taxes, insurances, breakdowns, etc. Those costs are presented in Table 2 and expressed in Colombian pesos ($COP).

Table 2 Unitary holding cost ($COP). 

Source: The Authors.

The maximum percentage of the total space that can be used to store the products in every functional area is defined in the company and equal to: a=65%, b=65% and c=65%. The requirement time of each product as a percentage of the total keeping time in the storage spaces is presented in Table 3 for each period.

Table 3 Assignment time of products as a percentage. 

Source: The Authors.

5. Results

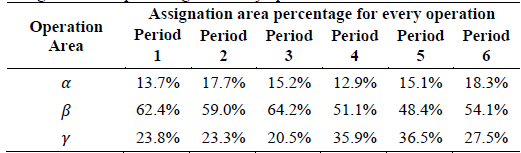
The proposed model for solving the design and dynamic storage allocation problem was programmed using the GAMS © software (version 24.4) and solved using the CPLEX 12.6 solver with the default parameters. All the computational tests were run on an Intel Core 2 Duo (2.2 GHz 4.0 GB) PC and the instances were generated from the operation of the studied food company. The results of the area assignment produced by the model are presented in Table 4.

Table 4 Assignation area percentage for every operation 

Source: The Authors.

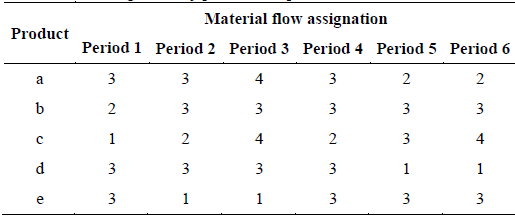
The total storage cost for the five products in the six periods is equal to COP$ 843,345,908. The flow assignment to the products in each period is presented in Table 5.

Table 5 Material flow assignation by product and period 

Source: The Authors.

The above results show the feasibility of the proposed model with the established restrictions, which effectively allocates the corresponding operation area and the material flow for the 5 products in the 6-period time horizon. This assignation corresponds to the minimal cost of the product assignment to each operational area in the warehouse, which is not easy to calculate without using the proposed model. As it is normal, the reserve space in the warehouse is the widest, since it is the operation area with the highest assigned area (the one with the highest percentage) in all periods. However, in other real operations, as can be the case of the mass consumption industry, this situation could be different, in which the larger areas could be assigned to cross-docking operations.

6. Conclusions

This paper presented a model for the successful storage allocation of several products to different operation areas in a warehouse in a defined time horizon aimed to reduce the holding and material handling cost for a food company. The model was applied in a Colombian food company for a storage system composed of 5 products, 3 different areas, 4 material flows and a time horizon of 6 periods. The model allows the simultaneous assignment of the products to the different areas (crossdocking, reserve, and shipping) and the dynamic assignation of the spaces in the warehouse in the several time horizons, in which the demands and the costs change.

For the solution of the storage allocation problem, an algorithm was proposed, which assures that all products are correctly assigned to a single operational area. This model is very important for companies that have large warehouses and lots of operations since the product allocation to the different areas looking for the minimization of the total cost is almost impossible without using mathematical approaches, such as the model presented in this paper.

As future research lines, it is expected to include stochastic demands in order to test the model performance and also consider other elements in warehouse design, such as the layout of the operation areas, as well as different warehousing systems.