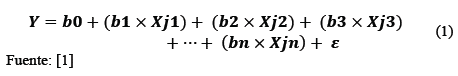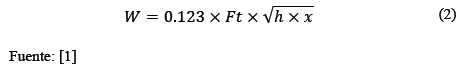1. Introducción
La PCA (Portland Cement Association) en su amplio portafolio de información sobre el cemento portland presenta un manual para el diseño de pavimentos industriales [1], el cual es ampliamente conocido, pero presenta dificultad al momento de evaluar diferentes alternativas de diseño de manera rápida, dado que se basa en cálculos manuales y en la lectura de varios nomogramas, también se presenta riesgo de error humano que está implícito al momento de la interpretación o lectura de los nomogramas.
En la fase de diseño de un pavimento se deben evaluar diferentes alternativas que permitan seleccionar la solución con mejor relación costo-beneficio. En la actualidad se presenta una dificultad practica en la aplicación del método de diseño PCA para pavimentos industriales, debido a la complejidad del método y el tiempo que requiere llevar a cabo una sola interacción de diseño, ya que así se cuente con los parámetros necesarios para el uso de los nomogramas del método, se vuelve complejo determinar los valores en estas gráficas con precisión. Además, en ciertas regiones existe un desconocimiento de este método, que ha llevado a que en varios proyectos los diseños se realicen con métodos que no aplican para este tipo de pavimentos, como el método PCA para diseño de pavimentos de concreto para carreteras, lo que ha llevado, en algunos casos a fallas prematuras y problemas de durabilidad en los pavimentos industriales, y en otros casos a sobrecostos por sobredimensionamiento del espesor de las losas.
Dadas las anteriores consideraciones, el principal objetivo de esta investigación fue el desarrollo de un soporte lógico que permita la aplicación repetida del método de la PCA para evaluar varias alternativas de diseño de pavimentos industriales de concreta manera rápida. La mayor dificultad para el desarrollo del software fue que las ecuaciones con las cuales se desarrollaron los nomogramas no están disponibles en la literatura científica, dado que no fueron publicadas con el método, en consecuencia, se optó por realizar modelos sustitutos de los nomogramas como base para desarrollar el software PCAindustrial.
2. Marco Conceptual
Los pavimentos industriales de concreto deben resistir constantes de cargas estáticas y dinámicas por lo cual su espesor debe ser suficiente para evitar fallas por este tipo de solicitación, por ello su diseño debe cumplir con las características exigidas según el uso que tendrá. A diferencia de los pavimentos de concreto para carreteras, que se diseñan para cargas de camiones, el diseño de pavimentos industriales de concreto también contempla cargas de montacargas, cargas puntuales y cargas distribuidas.
El diseño de pavimentos industriales incluye parámetros como número de repeticiones de carga montacargas, cargas puntuales y cargas distribuidas directamente sobre el terreno y la capacidad de soporte del suelo. Hay diferentes metodologías para el diseño de este tipo de pavimentos [2]. El método de la PCA utiliza los parámetros antes mencionados y con base en una serie de nomogramas permite calcular el espesor de las losas del pavimento. El espesor debe determinarse por fatiga, por carga puntual y por carga distribuida, dependiendo del uso que tendrá el pavimento se pueden descartar algunas de estas tres solicitaciones, sin embargo, para el diseño final se seleccionará el mayor espesor del resultante entre las solicitaciones consideradas.
2.1. Muestreo
Es una herramienta utilizada en investigación científica con propósito de seleccionar una parte representativa de una población para realizar estimaciones confiables sin necesidad de estudiar el total de la población. Para el caso de un muestreo para desarrollar un modelo sustituto, una de las consideraciones principales de las cuales dependerá la precisión, confiabilidad y por tanto utilidad del modelo es el muestreo al conjunto de datos del cual se pretende generar un modelo sustituto, si el muestreo es suficiente, el modelo será confiable.
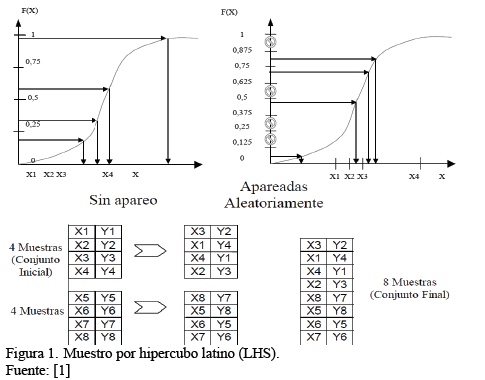
2.1.1. Muestro por hipercubo latino (LHS)
Para implementar un muestreo LHS se debe seleccionar las variables sobre las cuales se realizará la muestra y crear distribuciones de probabilidad sobre estas, luego se debe dividir la distribución en un número determinado de intervalos equiprobables adyacentes disjuntos en el eje de las ordenadas, generando un valor en las abscisas por cada intervalo, se debe generar una muestra para cada intervalo realizado y esto a su vez para cada variable (Fig. 1), posteriormente se realiza un emparejamiento entre las muestras de las distintas variables para así obtener vectores de valores de entrada (Fig. 1), el número de vectores debe ser igual al número de intervalos, cuando se realiza el emparejamiento se debe corroborar que el nivel de correlación entre estas sea bajo [3-7]. En el caso de realizar un muestreo con LHS para analizar las salidas de un modelo, el modelo se ejecuta por cada vector de valores de entrada que se tenga o sea que el número de veces que el modelo se ejecutará será igual a la cantidad de intervalos tomados en las distribuciones de probabilidad, independiente del total de variables escogidas. En este modelo solo es posible saber si el número de intervalos escogidos es suficiente con posterioridad a la ejecución del modelo numérico, en caso de no ser suficiente se debe empezar desde cero el procedimiento aumentando el número de intervalos por cada variable.
2.2. Modelo sustituto
Con frecuencia se utilizan las simulaciones como parte del diseño experimental en investigación para representar situaciones que requieren tiempo, planeación, personal, presupuesto y demás herramientas. Es común encontrar situaciones en las cuales un modelo complejo requiere gran cantidad de tiempo para su ejecución o un trabajo computacional fuerte y demorado. Muchas veces en ingeniería, al momento de llevar a cabo un diseño se deben considerar diferentes variables o parámetros aleatorios de los cuales depende un el resultado final y requieren métodos estadísticos para su modelación. Buscando la manera de optimizar estos procesos de análisis y diseño se introduce el concepto de modelo sustituto, el cual consiste en la creación de un modelo que represente los fenómenos de manera que se puedan llevar a cabo distintas simulaciones de manera rápida sin tener que realizar experimentos físicos o computacionales que consuman una elevada cantidad de recursos en tiempo, dinero, personal, planeación y demás herramientas [3, 5]. Es así como modelos complejos pueden ser reemplazados por modelos más simples sin sacrificar la precisión de los resultados. Estos modelos deben estar basados en una amplia gama de resultados experimentales garantizando que su precisión y veracidad sea la más óptima. Una de las posibilidades para elaborar un modelo sustituto es la realización de una regresión múltiple de los datos muestreados.
2.2.1. Regresión múltiple
La Regresión Múltiple tiene como objetivo principal encontrar una ecuación que prediga el resultado de una variable dependiente Y, a partir de un número N de variables independientes Xjn. También permite determinar cuál es la variación de la variable dependiente Y con base en las distintas variaciones de las variables independientes Xjn. Los coeficientes bn que acompañan a las variables independientes Xjn se determinan de manera paralela implementando el método de mínimos cuadrados, la expresión general de la regresión Múltiple está dada por la ecuación 1. El término
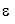 es referente al error que pueda darse al momento de realizar variaciones simultaneas en las variables independientes, esto con el fin de obtener una ecuación de manera completa y lo más aproximada posible al modelo que se desea representar.
es referente al error que pueda darse al momento de realizar variaciones simultaneas en las variables independientes, esto con el fin de obtener una ecuación de manera completa y lo más aproximada posible al modelo que se desea representar.
3. Metodología
El desarrollo del software se basó en la construcción de modelos sustitutos de los nomogramas del método de diseño PCA para pavimentos industriales. En primer lugar, se realizó muestreo LHS para cada nomograma, posteriormente con los datos del muestreo se desarrolló un modelo sustituto a partir de la regresión múltiple de los datos muestreados, luego de la verificación de la confiabilidad de los modelos se procedió a la codificación del software y finalmente se realizó una validación del software.
3.1. Tabulación y desarrollo del modelo sustituto
Utilizando LHS se procedió a realizar las tabulaciones de los nomogramas de la PCA para diseño de pavimentos industriales, teniendo tabulados los nomogramas de la PCA se lleva a cabo una regresión para desarrollar un modelo.
3.1.1. Cargas en eje con rueda simple
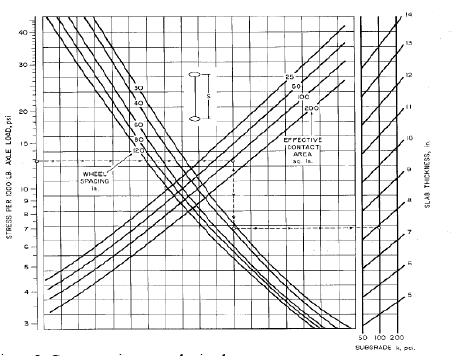
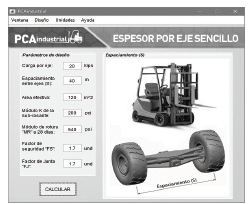
El nomograma de la PCA para diseño de pavimentos industriales por carga de montacargas con eje sencillo se muestra en la Fig. 2, este se compone por 4 variables independientes y 1 variable dependiente, la variable dependiente es el espesor de diseño por este tipo de carga, las variables independientes son [1].
Esfuerzo admisible por cada 1000 lb en el eje cargado: Este parámetro se calcula dividiendo el módulo de rotura del concreto entre un factor de seguridad y luego dividiendo el resultado entre el peso del eje en kips (1 kpi = 1.000 lb). El factor de seguridad se recomienda entre 1.7 y 2.0, el valor más alto se recomienda cuando se presenta frecuencia de ejes pesados.
Área Efectiva de contacto: Es el área de losa en contacto con una rueda. Si no hay datos disponibles, este parámetro se puede estimar, para ruedas neumáticas, dividiendo el peso del eje sobre la presión de inflado.
Espaciamiento entre ejes: Esta variable es el espaciamiento entre el centro de los ejes simples.
Módulo de reacción K: Esta variable corresponde al módulo de reacción K de la sub rasante del pavimento.
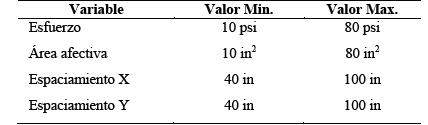
Los rangos máximos y mínimos de cada uno de los parámetros definidos para el muestreo LHS se indican en la Tabla 1.
3.1.2. Cargas en eje con rueda dual
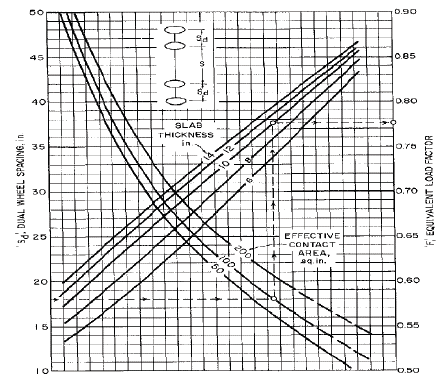
Para llevar a cabo el diseño de pavimentos industriales por carga de montacargas con eje dual se debe realizar la iteración entre los dos nomogramas de las Figs. 2 y 3, uno de estos nomogramas es el implementado para el diseño por carga de montacargas de eje sencillo, con el otro nomograma se convierten las cargas de montacargas de eje dual en cargas equivalentes de montacargas de eje sencillo (Fig. 3), por lo tanto en este apartado solo se explicaran los parámetros del nomograma de la Fig. 3 ya que en el apartado anterior se explicaron los parámetros para el nomograma de eje simple (Fig. 2).
El nomograma de la Fig. 3 incluye 3 variables independientes y una variable dependiente, la variable dependiente es el factor de reducción de esfuerzo aplicado al pavimento por cada 1.000 libras en el eje cargado, las variables independientes son [1]:
Espaciamiento dual entre ejes: Esta variable es el espaciamiento entre el centro de los ejes dobles, el eje simple no está involucrado en esta medida.
En la Tabla 2 se presentan los rangos de evaluación de estos parámetros considerados durante el muestreo LHS.
3.1.3. Carga en rack cuando modulo K=50 pci
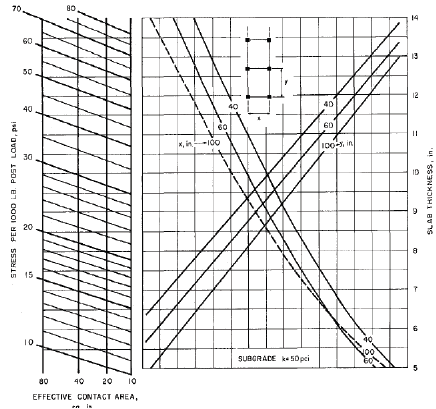
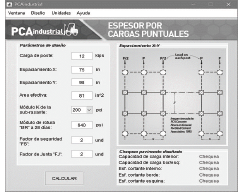
El nomograma de la PCA para diseño de pavimentos industriales por carga de rack (Carga puntual generada por estanterías) para sub-rasantes con modulo K=50 pci (Fig. 4.) se compone por 4 variables independientes y una variable dependiente, la variable dependiente es el espesor de diseño por este tipo de carga, las variables independientes son [1]:
Esfuerzo por cada 1.000 lb en poste cargado: Este parámetro se calcula dividiendo el módulo de rotura del concreto entre un factor de seguridad y luego dividiendo el resultado entre la carga del poste en kips (1 kpi = 1.000 lb). El factor de seguridad se recomienda entre 1.7 y 2.0, el valor más alto se recomienda cuando los racks son independientes y su altura es inferior a 35 pies.
Espaciamiento X: La variable hace referencia al espaciamiento transversal entre postes, la transversalidad es respecto al sentido más corto de la losa.
Espaciamiento Y: La variable hace referencia al espaciamiento longitudinal entre postes, con espaciamiento longitudinal hace referencia al sentido más largo de la losa.
Los rangos de cada uno de estos parámetros definidos para el muestreo LHS se indican en la Tabla 3.
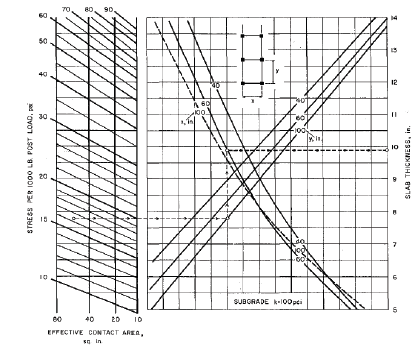
3.1.4. Carga en rack cuando modulo K=100 pci
El nomograma de la PCA para diseño de pavimentos industriales por carga de carga puntual generada por estanterías (rack), para sub-rasantes con modulo K=100 pci (Fig. 5), se compone por 4 variables independientes y 1 variable dependiente, la variable dependiente es el espesor de diseño por este tipo de carga, las variables independientes son [1]:
En la Tabla 4 se presentan los rangos de evaluación de estos parámetros considerados durante el muestreo LHS.
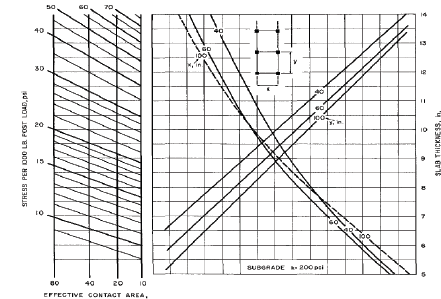
3.1.5. Carga en rack cuando modulo K=200 pci
El nomograma de la PCA para diseño de pavimentos industriales por carga de rack (Carga puntual generada por estanterías) para sub-rasantes con modulo K=200 pci (Fig. 6) se compone por 4 variables independientes y 1 variable dependiente, la variable dependiente es el espesor de diseño por este tipo de carga [1], las variables independientes y los rangos considerados en el muestreo LHS se indican en la Tabla 5
Tabla 5 Rango de valores para las variables de la carga en rack cuando modulo K=200 pci.

Fuente: [1]
3.1.6. Carga distribuida
Existen dos tipos de carga distribuida, las que tienen arreglo de carga definido y las que tienen arreglo de carga indefinido, la diferencia entre ambas es la configuración en que se distribuye la carga sobre la losa, si con pasillos de ancho constante o si la carga carece totalmente de configuración ordenada. Para la carga con arreglo definido el método de la PCA proporciona la ecuación (2) para determinar el espesor necesario para el pavimento. Por lo tanto, no fue necesario desarrollar un modelo sustituto en este caso y para la codificación del Software se utilizó directamente la ecuación.
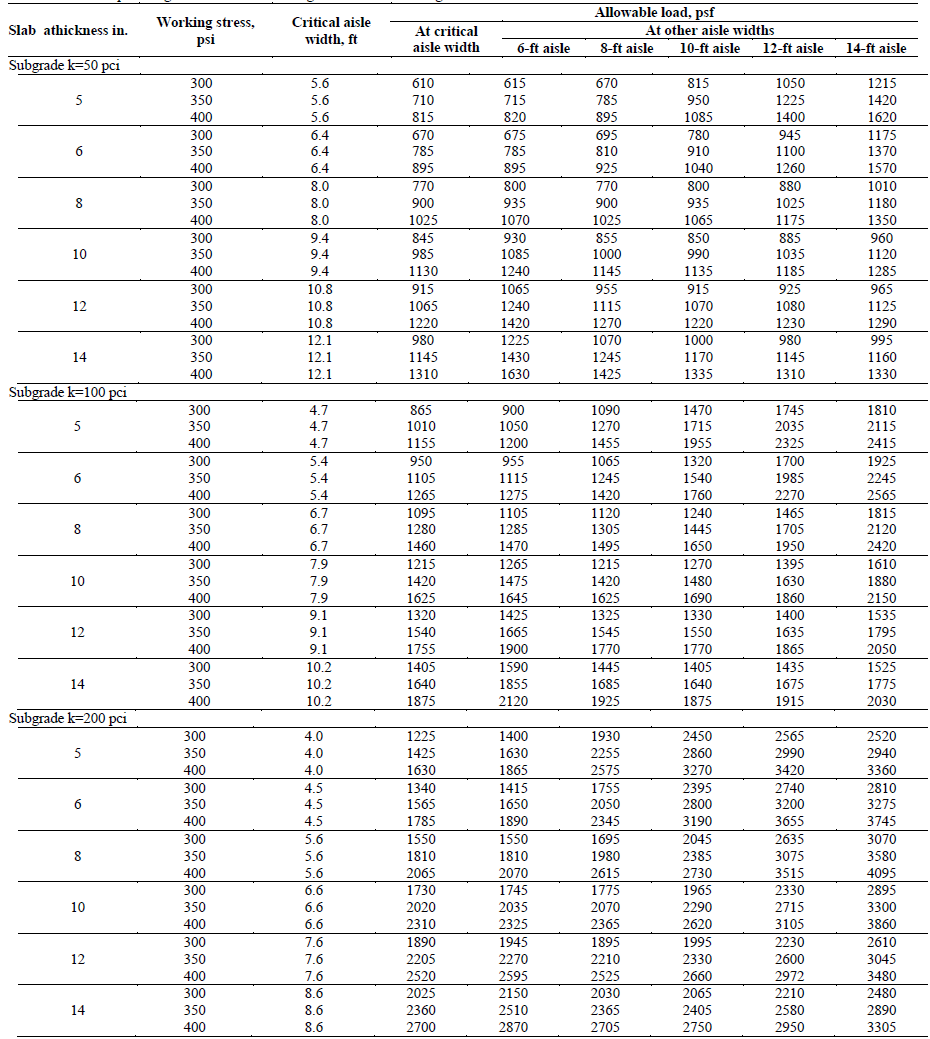
Para el caso de carga con arreglo no definido, el método de la PCA proporciona la Tabla 6, la cual esta subdivida en tres, una para un módulo K=50 pci, una para un módulo K=100 pci y otra para un módulo K=200 pci. Para utilizar alguna de las tres tablas, además del módulo K de la sub-rasante se debe tener el espesor de diseño, el esfuerzo de trabajo en el pavimento y un ancho de pasillo, con estos parámetros se obtendrá cual es la carga permisible en libras/pie2, aunque se trató de realizar un modelo sustituto para esta tabla y permitir que el usuario tuviera más libertad, sin estar limitado a los valores específicos de las tablas, no fue posible desarrollar un modelo sustituto con el nivel de confiabilidad aceptable, el R2 resultante fue del orden de 0.75 en el mejor de los casos. Por lo tanto, para el desarrollo del software se utilizó la tabla como esta propuesta en el método de diseño.
3.2. Realización del muestreo aleatorio con LHS
Posterior a identificar los parámetros de diseño para cada nomograma se procede con la ejecución del muetreo LHS por medio del software estadístico JPM®, este solicita datos como los rangos entre los cuales se encuentra cada variable y el número de iteraciones que se desean realizar para tener una muestra significativa. Las variables y sus rangos fueron explicados anteriormente en el numeral 3.1 del presenta artículo. Se ha sugerido que el tamaño del muestreo LHS sea mínimo 10 veces el número de variables independientes [8], en este caso ese número de variables independientes es de 3 o 4 según el nomograma, lo que implicaría LHS de tamaño 30 o 40 según el caso. Sin embargo, buscando mayor confiabilidad en los resultados, se trabajó con un número mínimo de 25 veces el número de variables independientes, es decir que para los casos de 4 variables el muestreo LHS contenía una muestra de 100 combinaciones de valores de las variables independientes.
Para cada muestreo LHS se determinó con los nomogramas la variable dependiente (espesor de la losa o factor de reducción en el caso del nomograma para carga de neumáticos con eje doble) para completar el conjunto de datos para construir el modelo sustituto mediante regresión múltiple.
4. Obtención de espesor para eje simple, eje doble y rack
Al obtener el LHS con las variables independientes del modelo, se procedió a determinar la variable dependiente Y a partir de los nomogramas, para cada para cada set de datos del muestreo LHS, La variable Y es el espesor de losa o el factor de reducción de esfuerzo según sea el caso, obtenidos de cada nomograma ingresando con esa combinación de parámetros, dicha combinación está conformada de tal manera que se obtiene el muestro necesario para determinar un modelo sustituto. Para lograr interactuar con los nomogramas con la mejor precisión se utilizó el software AutoCAD®, esto con el propósito de digitalizar la imagen y lograr un aumento máximo sobre esta (zoom) y así obtener precisión de milésimas de pulgada en el resultado del espesor para el pavimento industrial según la combinación determinada para cada iteración. Aplicando la herramienta cota de AutoCAD® y la herramienta de creación de líneas perpendiculares se logra realizar una interpolación pudiendo dar la precisión en cifras decimales requerida por el LHS.
Carga por montacargas de eje Sencillo: El procedimiento para realizar la lectura en el nomograma (Fig. 2) de la PCA para diseño de pavimentos industriales por la carga mencionada consiste inicialmente en determinar el esfuerzo (E) por cada 1000 lb de carga en el eje cargado, E=MR/(FSxP), el factor de seguridad (FS) es un factor que determina el diseñador, la carga P hace referencia a la carga en el eje cargado y el módulo de rotura MR, posterior a esto se procede a ingresar en el nomograma por el eje vertical izquierdo ubicando el valor obtenido de esfuerzo, se traza una línea horizontal hasta llegar al valor de diseño en el area efectiva de contacto, luego se traza una línea vertical hasta llegar al valor de diseño para el espaciamiento del eje, posteriormente trazo una línea horizontal hasta cortar el valor de diseño para el Modulo K de la sub-rasante, cuando se llega al valor del módulo K se debe leer en el eje vertical de la derecha el espesor de diseño necesario para cumplir los parámetros con los cuales se ingresó al nomograma.
Carga por montacargas de eje Dual: El procedimiento para realizar la lectura en el nomograma (Fig. 3) de la PCA para diseño de pavimentos industriales por la carga mencionada consiste inicialmente en ingresar al nomograma por el eje vertical izquierdo con el valor de espaciamiento dual, posterior a esto se traza una línea horizontal hasta llegar al valor de diseño para el area efectiva de contacto, luego se traza una línea vertical hasta llegar al valor supuesto de diseño para los parámetros de diseño, aquí toca suponer un posible espesor que supla las necesidades de diseño, sin importar que valor que se tome, al cabo de varias iteraciones el resultado tiende a la convergencia, se sugiere un valor inicial supuesto de 10 in, posterior a esto se traza una línea horizontal hasta obtener el factor de disminución de carga en el eje vertical derecho. Ahora se debe realizar el procedimiento mencionado anteriormente para eje sencillo, pero en este caso la carga P será la Carga del eje dual multiplicada por el factor de minoración, luego se aplica la fórmula para esfuerzo y se sigue el procedimiento para eje sencillo, al final del procedimiento se compara el espesor obtenido con el supuesto, si tiene un error mayor a 0.1 in entonces se repite este procedimiento ingresando en el valor de espesor el obtenido con anterioridad.
Carga por Rack (Cargas puntuales por estanterías): El procedimiento para realizar la lectura correcta en el nomograma de la PCA para diseño de pavimentos industriales por la carga mencionada consiste inicialmente en ingresar en la parte inferior izquierda el área efectiva de contacto, se traza una línea vertical y se continua con la determinación del esfuerzo (E) por cada 1000 lb de carga el poste de mayor carga,
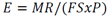 , el factor de seguridad es un factor que determina el diseñador, la carga P hace referencia a la carga en el poste y el módulo de rotura MR, siguientemente se procede a ubicar el valor del esfuerzo por cada 1000 lb en el eje vertical izquierdo ubicando el valor obtenido de esfuerzo, se traza una línea horizontal hasta llegar al valor de diseño para el espaciamiento denotado como Y, luego se traza una línea vertical hasta llegar al valor de diseño para el espaciamiento denotado como X, posteriormente trazo una línea horizontal hasta cortar el eje vertical derecho y leer en este el espesor de diseño necesario para cumplir los parámetros con los cuales se ingresó al nomograma (Figs. 4, 5 y 6).
, el factor de seguridad es un factor que determina el diseñador, la carga P hace referencia a la carga en el poste y el módulo de rotura MR, siguientemente se procede a ubicar el valor del esfuerzo por cada 1000 lb en el eje vertical izquierdo ubicando el valor obtenido de esfuerzo, se traza una línea horizontal hasta llegar al valor de diseño para el espaciamiento denotado como Y, luego se traza una línea vertical hasta llegar al valor de diseño para el espaciamiento denotado como X, posteriormente trazo una línea horizontal hasta cortar el eje vertical derecho y leer en este el espesor de diseño necesario para cumplir los parámetros con los cuales se ingresó al nomograma (Figs. 4, 5 y 6).
5. Desarrollo del modelo sustituto eje simple, eje doble y rack
Teniendo el resultado de cada una de las iteraciones realizadas (espesor de pavimento con esas condiciones de diseño) se ingresan al software JPM® para continuar con el desarrollo del modelo sustituto, JPM® ofrece diferentes metodologías para hallar modelos sustitutos teniendo el espacio muestral, en este caso se trabaja con regresión múltiple, cuando se desarrolla el método de regresión múltiple en JPM® este arroja una serie de combinaciones entre las variables independientes, a su vez muestra la incidencia de cada una de las variables en el modelo. Posteriormente el modelo obtenido se ejecutó para evaluar los resultados obtenidos antes de intentar una validación del modelo, algunos análisis que se realizaron fueron: Revisión del coeficiente de determinación, se buscaba que como mínimo fuera 0.99, comparación gráfica del ajuste ordinario de mínimos cuadrados que realiza el software, el objetivo de esto era determinar que iteraciones estaban generando el error y poder descartarlas del análisis, comparación grafica de los residuales del modelo sustituto con el mismo propósito que la comparación anterior, cuando se lograba calibrar un modelo que cumpliera con los limites planteados entonces se procedía a tomar la ecuación del modelo sustituto y continuar con una etapa de pre validación.
6. Desarrollo del Software PCAindustrial
Para el desarrollo de PCAindustrial se utilizó MATLAB®, este ofrece un entorno de desarrollo integrado para la creación de la interfaz gráfica, este posee su propio lenguaje de programación, el lenguaje M. Se construyó un entorno de ventanas que contienen los elementos básicos para el diseño en cada caso, se tiene una ventana para cada tipo de diseño, ventana de bienvenida la cual tiene como propósito dar información básica de PCAindustrial y la bienvenida al programa, ventana de información del proyecto que tiene como propósito registrar la información del diseñador, una ventana de diseño para eje simple, ventana de diseño para eje doble, ventana de diseño para carga en rack y ventana de diseño para carga distribuida, cada una de las ventanas mencionadas anteriormente tienen como objetivo recopilar la información necesaria para el diseño según sea el caso. La interfaz de PCAindustrial cuenta con al menos 11600 líneas de código contenidas en 12 archivos con extensión .Mat, están son digitadas en su totalidad sin utilizar la herramienta para diseño de interfaz que proporciona Matlab, ya que el digitar las líneas una a una se tiene mayor control sobre el código que se programa, la función de tiene cada línea y se optimizan los recursos que consumirá el software desarrollado.
7. Validación del Software PCAindustrial
Por medio de pruebas de escritorio se procedió a realizar la validación de PCAindustrial, esta consistió en comparar diseños hechos con el método manual y los mismos diseños realizados implementando PCAindustrial.
7.1. Validación inicial del modelo sustituto en su desarrollo
Se realizaron 3 validaciones para corroborar que el modelo sustituto desarrollado fuera confiable y cumpliera con el error máximo previsto como objetivo, la primera de esas validaciones se realiza con los 100 datos iniciales del LHS usados para desarrollar el modelo sustituto, se toman los valores obtenidos de los nomogramas en cada iteración y se comparan contra los valores obtenidos por el modelo sustituto usando los mismos parámetros en cada iteración, en todos los casos se obtiene que el error en los 100 datos es menor a los 4mm que es el error máximo permisible. Esta validación simplemente se realizó de manera exploratoria para evaluar el comportamiento del modelo sustituto, debido a que se realizaba con los mismos datos de LHS para el desarrollo del modelo. Las validaciones definitivas se realizaron con datos diferentes a los utilizados en la construcción del modelo sustituto.
7.2. Validación final del modelo sustituto definido
La validación final del modelo se realizó de manera similar a la validación anterior, pero se generó un nuevo campo muestral de 50 iteraciones en las cuales se determinó el espesor en cada nomograma y comparándolo con el resultado que arrojaba el modelo al introducirle los mismos parámetros.
7.3. Validación de Software PCAindustrial
Como se indicó anteriormente, para la validación se realizaron nuevos muestreos LHS, con tamaños del orden 50 iteraciones para cada uno de los modelos a validar. El muestreo se realizó de igual forma que la descrita anteriormente para determinar los datos de las variables independientes, posteriormente se procedió a ingresar los parámetros muestreados en PCAindustrial, esto para realizar una doble validación, es doble validación ya que se valida de nuevo el resultado y la precisión del modelo sustituto y adicionalmente se valida la programación de fondo de PCAindustrial, que este cumpliendo su función sin modificar el resultado final del modelo sustituto y sin errores de programación.
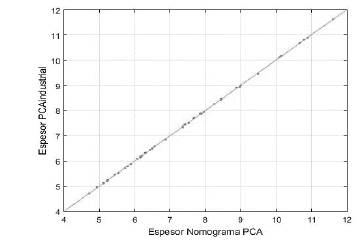
Las Figs. 7, 8, 9, 10 y 11 muestran los resultados de la validación, los resultados muestran alta similitud entre el diseño utilizando los nomogramas y el software PCAindustrial.
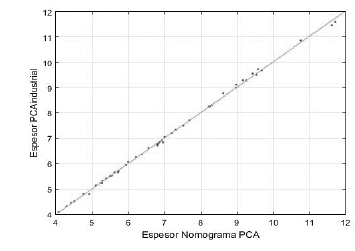
Fuente: Los Autores
Figura 7 Comparación gráfica del ajuste ordinario de mínimos cuadrados para diseño en carga por eje sencillo.
7.3.1. Validación de PCAindustrial para diseño en carga por eje sencillo
La Fig. 7 muestra los resultados de validación para el diseño por carga de eje sencillo, se observa alta precisión del Software en comparación con los resultados obtenidos con la lectura manual del nomograma. Entre más cercanos se encuentren los puntos a la línea de 45°, más precisión posee el software PCAindustrial. Aunque algunos puntos no caen exactamente en la línea de 45° esto no representativo al momento de comparar los resultados.
7.3.2. Validación de PCAindustrial para diseño en carga por eje dual
La Fig. 8 muestra los resultados de la validación del diseño por carga de eje dual, se observa alta precisión en los resultados, en este caso se observa que los puntos están mucho más cercanos a la línea de 45° que en el grafico anterior, esto en parte es debido a que el nomograma cuenta con solo 3 variables independientes permitiendo generar un modelo sustituto más preciso.
7.3.3. Validación de PCAindustrial para diseño por carga en rack en un suelo con modulo K=50 pci, 100 pci y 200 pci respectivamente
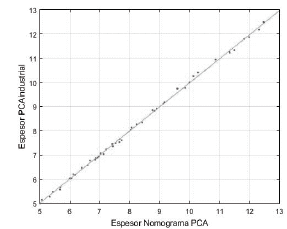
De las Figs. 9, 10 y 11, que representan la validación de los diseños por carga en rack en un suelo con modulo K=50 pci, 100 pci y 200 pci respectivamente, se observa una alta precisión de PCAindustrial ya que los puntos están muy ajustados a la línea de 45°.
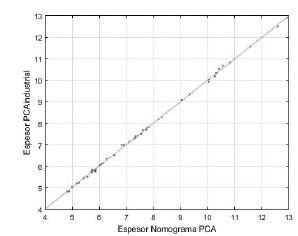
Fuente: Los Autores.
Figura 9 Comparación gráfica del ajusteordinario de mínimos cuadrados para diseño porrack en un suelo con módulo de K=50 pci.
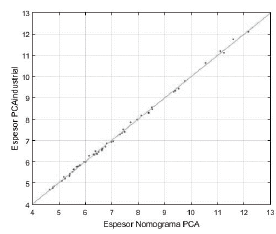
Fuente: Los Autores.
Figura 10 Comparación gráfica del ajuste ordinario de mínimos cuadrados para diseño por rack en un suelo con módulo de K=100 pci.
Fuente: Los Autores
Figura 11 Comparación gráfica del ajuste ordinario de mínimos cuadrados para diseño por rack en un suelo con módulo de K=200 pci.
8. Software PCAindustrial para diseño de pavimentos industriales de concreto
El software PCAindustrial desarrollado en esta investigación es un soporte lógico del método de la PCA para diseño de pavimentos industriales de concreto. Fue implementado a partir de modelos sustitutos de los nomogramas presentados en la publicación “Packard, Robert G. Slab thickness design for industrial concrete floors on grade. Portland Cement Association, 1996” [1].
PCAindustrial permite calcular los espesores requeridos en losas de concreto simple para pavimentos y pisos industriales sometidos a cargas de montacargas de eje sencillo o doble, cargas puntuales por postes de estantería y cargas distribuidas con arreglo definido o no definido.
La Fig. 12 muestra la portada principal de PCAindustrial, el software es de uso libre, los instaladores y el manual de usuario pueden ser descargados del siguiente link. https://sites.google.com/a/correounivalle.edu.co/pcaindustrial/home
9. Ejemplo:
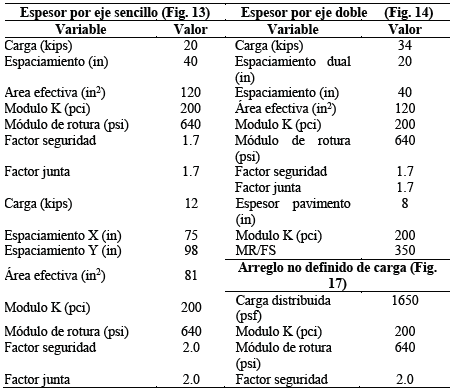
A continuación, se presenta un ejemplo de diseño de un pavimento industrial de concreto con el Software PCAindustrial teniendo los siguientes datos:
El programa calcula los espesores requeridos para cada tipo de solicitación de carga que experimentará el pavimento de concreto. Se puede seleccionar la condición más crítica para un espesor de losa homogénea o si el proyecto lo permite recomendar los espesores de losas para áreas determinadas.
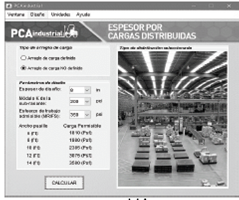
Fuente: Los Autores
Figura 16 Cargas permitidas para un espesordeterminado en cargas distribuidas con arreglo no definido de carga.
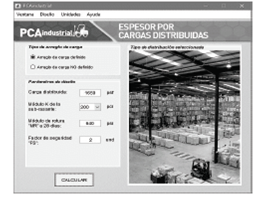
Fuente: Los Autores.
Figura 17 Diseño de espesor por cargas distribuidas con arreglo definido de carga.
10. Conclusiones
La investigación muestra cómo se pueden utilizar los modelos sustitutos para desarrollar software de metodologías de diseño aún vigentes que están soportadas con base en nomogramas de los cuales no se conocen las ecuaciones o datos a partir de las cuales se generaron.
En el muestreo LHS se encontró que la recomendación encontrada en la literatura, respecto a qué el tamaño del muestreo sea como mínimo igual a 10 veces en número variables independientes, es confiable y que posiblemente implementando un muestreo mayor no se logra aumentar considerablemente la precisión.
El trabajo realizado incluye muestreos aleatorios estratificados, verificaciones, análisis de los resultados, análisis de las gráficas, verificaciones para minimizar las diferencias entre el resultado obtenido con el modelo sustituto y con el nomograma de la PCA y validación del software para garantizar una buena precisión de los resultados del software PCAindustrial.
El software PCAindustrial facilita el uso de la metodología de la PCA para diseño de pavimentos industriales. Con él se pueden realizar evaluaciones rápidas de varias alternativas de diseño y se reduce el error humano en las lecturas repetidas de nomogramas.