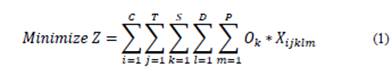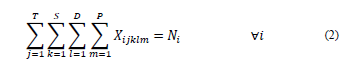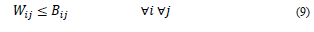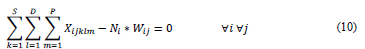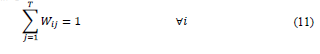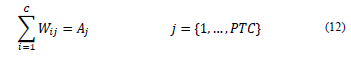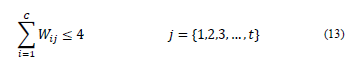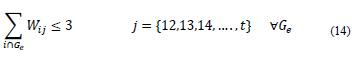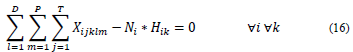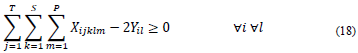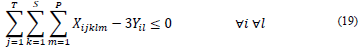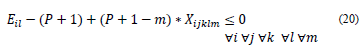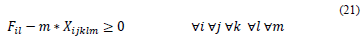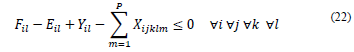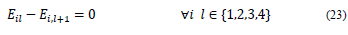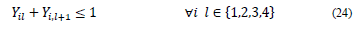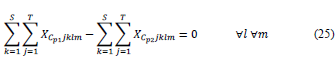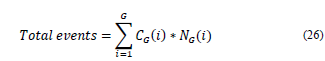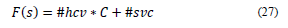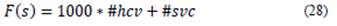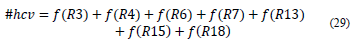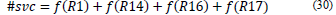1. Introduction
The university course timetabling problem, better known by its acronym in English as UCTP, is an activity that allows institutions of higher education to satisfactorily fulfill their mission. This is a demanding task, with a high degree of difficulty that, if not done properly, could compromise the entire process of student training. A deficient schedule might generate a serious set of issues that could go from discomfort in members of the university community (teachers, administrators and students) until the waste of resources (finances, time, physical and personal exhaustion). Due to this, professionals and researchers have studied the dynamics of this phenomenon during the last 50 years.
The UCTP is a problem of combinatorial optimization of the NP-hard type [8]. In this problem a set of courses must be assigned to a set of classrooms during a period of time, considering a series of restrictions predefined by the institution. The requirements and needs of each university cause a large number of variants of the UCTP, even in universities in the same country. As a consequence, different methods have been used to address the schedule programming issues of universities around the world. As described above, this research seeks to address the problem of University Course Programming in order to facilitate this administrative work.
The document is organized as follows. Section 2 presents a literature review about the UCTP. In section 3 the definition of the problem and its corresponding mathematical composition in MILP is carried out. Section 4 describes the operation of the Hybrid Genetic Algorithm Tabu Search, HGATS. Section 5 contains the experimental design carried out to define the parameters in each of the instances and the corresponding results. Finally, section 6 and 7 present the conclusions and recommendations for future research, respectively.
2. Literature review
The university courses programming is part of a wide group of programming problems, commonly known as "Timetabling". These problems can be defined in a general way as the allocation of a set of events to a space and time fulfilling a series of restrictions that involve a limited set of resources [11].
The scheduling problems have repercussions in several aspects of the study training process such as education, transportation, sports, health, etc. Particularly, in the case of education, [12] divided the problem into three types: scheduling of schedules in schools, programming of exams and programming of university courses; We shall concentrate in the last type, which is the one that occupies the present work.
The study of this phenomenon began with Gotlieb in 1963. Since then, professionals and researchers have been proposing different methods and procedures to solve the UCTP problem. [15] solved the first problem of schedules using the graph coloring problem; in their research, they reduced the problem to a series of vertices (courses) and arcs (conflicts) where the periods were represented by colors; however, this approach failed to address large instances of the problem.
In 2002, the first edition of the International Timetable Competition (ITC-2002) organized by Metaheuristic Networks was held. In this event a typical problem with three hard restrictions and three soft constraints was proposed together with a set of 20 instances with the objective that researchers and professionals apply different methods to address the problem. In later years this problem and its instances were used as a reference for more researchers to test the effectiveness of their own solution techniques.
In 2005, [6] published what would be the first integer formulation that explicitly considered a wide range of requirements, which made it a computationally challenging problem. The authors worked on the programming university courses problem at the Faculty of Engineering of Sannio University in Italy as a linear programming problem where they implemented two families of cutting planes as relaxation methods, Clique and Lifted Odd-Hole inequalities, and developed a Branch-and-Cut algorithm capable of finding optimal solutions from a set of real-world instances.
Subsequently, [13] defined a mixed integer multi-objective programming model to address the UCTP problem of the School of Economics and Management of the University of Hannover. In this model, the requirements that would generally be considered as hard constraints were incorporated in the objective function and penalized according to the importance of the restriction in order to guarantee an "optimal" solution with the least number of conflicts.
In 2010, [4] proposed a Harmonic Search Algorithm (MHSA). This metaheuristic was tested with 11 instances of 'Socha benchmark' achieving the best solutions registered to date in two of the most complex instances. In that year, them modified their algorithm introducing five new movements in tone adjustment (HSA-MPAR), however, this did not exceed the performance of the metaheuristics used initially. Later, [5] created a new harmonic hybrid search algorithm (HHSA), this new algorithm was based on the MHSA, proposed by the authors in their previous work, introducing a Hill Climber optimizer that is applied every time a new harmony is generated. At the time of comparison, it was found that the HHSA exceeded the previous proposals made by the authors.
In 2014, [10] proposed a two-phase algorithm. In the first phase a feasible initial solution is generated by assigning randomly ordered events to an empty schedule while the hard constraints are met. In the second phase, a Partial Random Neighborhood Tabu Search algorithm known as RPNS (Random Partial Neighborhood Search) is responsible for improving the quality of the solution, in this technique two structures of variable-sized neighborhoods are used to exchange the events of each candidate. In the experimentation, the RPSN proved to be highly effective when evaluating 5 medium instances and 1 large instance of Socha (2002).
In 2015, [2] designed an Adaptive Acceptance Criterion (AAC) algorithm. The author proposed a mechanism similar to that used in ARDA to escape local optima. The algorithm was evaluated in 11 instances of Socha (2002) and when compared with other techniques in the literature it only matched them in small instances.
In 2016, [14] proposed a linear programming model to address the UCTP of the Faculty of Economics and Business of KU Leuven in Belgium. In this problem it was considered the displacement between the faces as a goal to be reduced. Given the size of the problem, the authors proposed a two-stage model. In the first phase, a timetable is sought that meets the hard constraints of the problem and minimum responses in the preferences of the teachers, while the second phase uses the schedule of the first stage as the input with the objective of minimizing the flow of students through the reassignment of events to classrooms.
In 2017, [7] proposed a multi-objective programming model to address the problem CB-CTT of the International Competition of Schedules of 2007. Given the complexity of the problem and the high execution time, the authors applied five cuts as methods of relaxation. When the model was evaluated, it was possible to match the best solution in two reference instances of Track 3 of ITC-2007 in less than 15 minutes.
3. Description and mathematical formulation of the problem
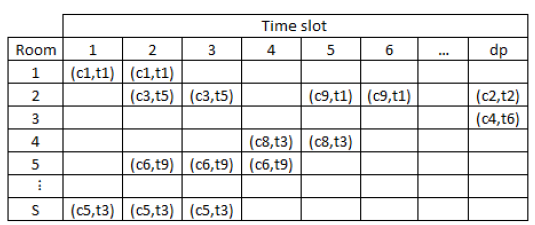
According to [3], in general, the problems of programming university courses involve assigning a set of courses (events), teachers and students to a fixed number of time slots and classrooms attached to various restrictions. The restrictions of this problem can be classified as hard and soft. The goal of establishing schedules is to fulfill all the hard constraints and try to satisfy the soft constraints as much as possible (to produce a high quality schedule). A schedule can be represented as a two-dimensional matrix where the rows correspond to the classrooms and the columns represent the time slots. Each pair (classroom-time slot) is a space in which a course and a teacher can be assigned. Fig. 1 presents the outline of a generic timetable.
3.1. Subject programming
For this research project, we consider the problem of UCTP known as CB-CTT (Curriculum-based Course Timetabling). This branch is characterized by planning the schedules based on the curriculum of the academic program and considering a projection of the number of courses that would be required in the next semester.
The most relevant aspects for this problem are: subjects, teachers, classrooms and slots available during a week and then replicate this week throughout the current semester. Here are some important definitions:
Academic levels: The subjects of the Industrial Engineering program are classified into academic levels; these levels range from level 1 to 10.
Curriculum: A curriculum is a set of courses of the same academic level that are expected to be attended by the same group of students, this definition is used in order to avoid the time interference between the classes, when the students enroll to them.
Courses: The subjects to be programmed are those included in the Curriculum for the professional career of Industrial Engineering, this includes mandatory courses, elective courses and service courses.
Mandatory courses: Are those that the University considers, within the respective curriculum, for mandatory registration and approval.
Elective courses: These are the ones that the University has established in the respective curriculum, in order to contribute to professional training.
Service courses: These are the subjects of the respective curriculum that are required by other academic programs and would share resources with the mandatory and elective courses.
Additionally, according to the modality of the teaching-learning process, the subjects are classified as:
Theoretical: Are those in which the teaching-learning process is carried out through the teacher's presentations, with the participation of the students.
Practices: Are those in which the teaching-learning process is carried out by the student applying the theoretical knowledge, under the guidance of the teacher.
Theoretical-practical: Are those in which the teaching-learning process is carried out combining the two previous modalities of class.
Each class has a number of courses to be programmed. Furthermore, each of them has an academic intensity measured in weekly hours, which translates into the number of events to be scheduled.
Teachers. They are full-time, part-time or chair staff hired by the institution to teach one or more courses. The programming of subjects for teachers depends on their classification, whether it is a plant type, a chair or a Postgraduate student.
Full-time professor: Performs the function of direction of classes under the modality of full-time professor. Regarding the programming of subjects, the Full time teacher is allowed to define the subjects and number of courses per class that he or she can teach.
Part-time professor: Performs the function of direction of classes temporarily. His or her employment relationship is governed by a labor contract for the time that is required. For the programming of subjects, the teacher proposes the subjects that he or she can teach.
Postgraduate student: Carries out the work of consideration under the modality of direct teaching in undergraduate, prior agreement with the School Council, to teach a course of a class with a maximum weekly intensity of 6 hours.
Moreover, it should be taken into consideration that there is a maximum number of courses that can be assigned to a teacher, which is defined by the Program Management. Finally, teachers in general have a weekly hourly availability in which they can teach their classes.
Physical space. It is considered that the program has associated a classroom building that is composed of classrooms, classroom workshops, laboratories, computer rooms, master's room, teachers' lounge and administrative offices.
Periods and time slots. The periods correspond to the time periods in which a day is divided and generally, they have a duration of one hour. The slots correspond to the totality of the periods available during a week.
3.2. Restrictions of the problem
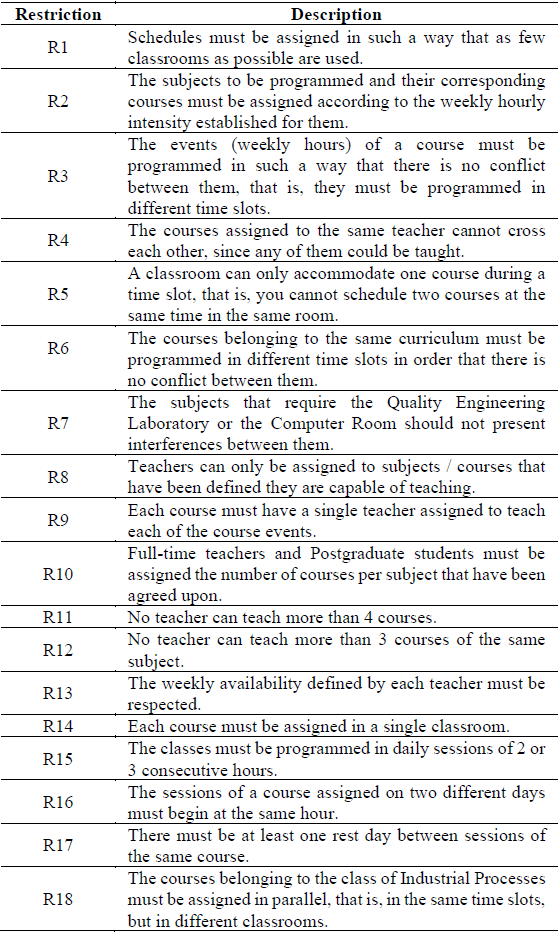
The requirements and needs establish the type of schedules that are sought to produce. These needs translate into the restrictions of the problem, which are summarized in Table 1.
3.3. Mathematical formulation for UCTP
Based on what is described in section 3.1 and 3.2, it is possible to propose the subject programming of the Industrial Engineering program in EEIE as a problem of mixed integer linear programming - MILP. Next, the necessary elements to solve the problem would be defined.
Input
i={1,2,3,…,c} Courses (c) that must be programmed.
j={1,2,3,…,t} Available teachers (t).
k={1,2,3…,s} Available classrooms (s).
l={1,2,3…,d} Days (d) of the week.
m={1,2,3…,p} Available Periods (p).
Q h ={1,2,3,…,h} Currículum. v
Ge={1,2,3,…,e} Subjects.
i∩Q h : Subset created from the sets Courses and Curricula to identify which courses belong to each curriculum
i∩G e : Subset created from the sets Courses and Subjects to identify which courses belong to each subject
iLAB : Subset that contains the courses of the subjects that must be programmed in the Quality Engineering laboratory.
iCOM : Subset that contains the courses of the subjects that must be programmed in the computer room.
N i : Number of weekly hours that the course i must be programmed.
A j : Number of courses that Full-time teachers must teach.
B ij : Availability matrix, which has a value of 1 if the course i can be taught by the teacher j.
V jlm : Availability matrix, which has a value of 1 if the teacher j is available to teach any course on the day l in the period m. Availability matrix, which has a value of 1 if teacher j is available to impart day l in period m.
O k : Coefficient Vector, which has an integer value that varies from 1 to "s" and penalizes if classroom k is assigned.
Once the elements that stay in the formulation have been defined, the variables, the objective function and the restrictions that guarantee the feasibility of the schedule are defined.
Variables
Xijklm={(1 if teacher j teaches the course i in classroom k on day l in period m@0 if not)
W ij ={1 if teacher j teaches course i@0 if not)
H ik ={(1 if course i is taught in classroom k@0 if not)
Y il ={1 if the course i is taugth on day l@0 if not)
E il∈N First period assigned to course i on day l
F il∈N Last period assigned to course i on day l
Problem model in MILP
The approach is made considering a mono-objective function attached to 25 equations grouped in 18 restrictions.
R1. The objective of the model is to program the schedules in such a way that the minimal possible amount classrooms is used
Subject to:
R2. The subjects to be programmed and their corresponding courses must be assigned according to the weekly hourly intensity established for them.
R3. The events (weekly hours) of a course must be programmed in such a way that there is no conflict between them, that is, they must be programmed in different time slots.
R4. The courses assigned to the same teacher cannot cross each other, since any of them could be taught.
R5. A classroom can only accommodate one course during a time slot, that is, two courses cannot be scheduled at the same time in the same room.
R6. The courses belonging to the same curriculum must be programmed in different time slots in order that there is no conflict between them.
R7. The subjects that require the Quality Engineering Laboratory or the Computer Room should not present interferences between them.
R8. Teachers can only be assigned to subjects / courses that have been defined they are capable of teaching.
R9. Each course must have a single teacher assigned to teach each of the course events.
R10. Full-time professor and Postgraduate students (PTC) must be assigned the number of courses per subject that have been agreed upon.
R11. No teacher can teach more than 4 courses.
R12. No teacher can teach more than 3 courses of the same subject.
R13. The weekly availability defined by each teacher must be respected.
R14. Each course must be assigned in a single classroom.
R15. The classes must be programmed in daily sessions of 2 or 3 consecutive hours.
R16. The sessions of a course assigned on two different days must begin at the same hour.¿
R17. There must be at least one rest day between sessions of the same course.
R18. The courses belonging to the class of Industrial Processes C p(i) must be assigned in parallel, that is, in the same time slots, but in different classrooms.
4. HGATS algorithm applied to the described UCTP problem
4.1. Representation of the solution
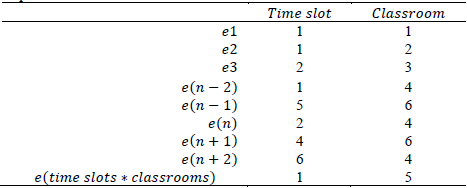
In this case, the solution is represented by a list of time slot-classroom pairs composed of all possible combinations of classrooms and time slots, where the index of the first n pairs is the identifier of each event and the pairs numbered after the event n, represent the pairs that have not been assigned.
Regarding the events, the Fig. 2 shows each event contains information about the class, the course to which it belongs, and the professor who attended the event.
Being, G the set of subjects, C G the number of courses per subject and N G the weekly hourly intensity of each subject. The total number of events n to be programmed is defined by:
In the solution presented in Table 2, event 1 has been assigned on strip 1 of room 1, event 2 on strip 1 of room 2; while, room 6 on strip 4 is unoccupied. In this way, compliance with restrictions R2 and R5 is guaranteed.
4.2. Fitness function
A Fitness function is established to minimize violations of hard and soft restrictions. The fitness function F(s) for solution s, is defined as the sum of the number of violations of hard restrictions #hcv and soft restrictions #scv.
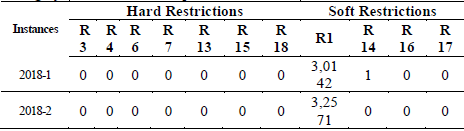
Hard Restrictions: Restrictions classified as hard must be satisfied in full to consider that the solution is feasible, these constraints are R2, R3, R4, R5, R6, R7, R8, R9, R10, R11, R12, R13, R15 and R18. From this group, the restrictions R2 and R5 are guaranteed in their entirety due to the representation of the solution, since it always guarantees that all events are programmed and there is no time interference among the classrooms. Additionally, the restrictions from R8 to R12 are fully guaranteed through the Teacher Assignment Heuristic which randomly links a course with a teacher, while satisfying those restrictions.
Soft Restrictions: These restrictions measure the quality of the solution; the quality of the solutions is appropriated if it satisfies these restrictions in the best possible way. The soft restrictions are R1, R14, R16 and R17.
The value of constant C is 1000. In this way, it is guaranteed that during the search process, the hard restrictions will be prioritized over the soft ones. Finally, the aptitude function is expressed as:
4.3. Adaptation of the algorithm
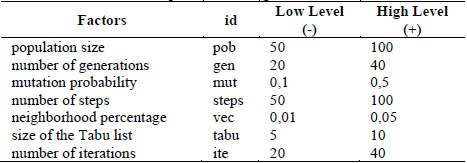
It starts by defining the instance and the values of the parameters involved. For the first stage of the HGATS algorithm, the parameters of population size, number of generations, mutation probability and number of steps guide the evolution of the GSGA algorithm; whereas, in the second phase, the TS algorithm is governed by the parameters of neighborhood percentage, size of the Tabu list and number of iterations.
In GSGA, initially, the Teacher Assignment Heuristic is executed, which links teachers and courses; then, the Genetic Algorithm constructs the population of initial solutions using the Initialization of Individuals algorithm and the Local Search operators 1 and 2; then, the process of evolution is passed, there, the Crossing and Mutation operators generate a new solution, which is improved by Local Search operators 1 and 2; then, the worst solution of the population is selected and replaced with the recently generated solution. This procedure is repeated until the defined number of generations is reached. Finally, the Room Stability Heuristic is applied on the best solution obtained and its aptitude is evaluated. If the solution is optimal, the algorithm stops.
The TS algorithm is executed only if the best solution generated in the first phase is not optimal, that is, if F(s)>0. In this phase, a Taurus Search heuristic is applied, using of N1 and N2 as neighborhood structures to move the solution in the search space. During each iteration, the penalty of each of the possible movements is calculated and the best of them is made. With each movement the tabu list is updated and some movements are restricted for future iterations. Once the defined number of iterations is fulfilled, the Tabu Search heuristic shows the best solution found so far and applies the Salon Stability Heuristic on the solution.
4.3.1. Teacher assignment heuristics
This heuristic is in charge of randomly assigning the professors to the courses while guaranteeing the fulfillment of the restrictions R8, R9, R10, R11 and R12.
The algorithm starts by ordering the subjects according to the number of teachers available for each one of them; then, the algorithm selects the list of possible teachers who can teach the subject. If there is a Full-time professor or Postgraduate Student who can teach the subject, we proceed to assign the number of courses required by the teacher for that subject. If there are more courses to be assigned, it will be linked to the Chair professors, guaranteeing that they cannot teach more than 3 courses of the same subject, neither allowing them to teach more than 4 courses in total.
4.3.2. Blocks.
In order to limit the search space in feasible regions, we have chosen to introduce the concept of blocks. To do this, it has been determined that the events should be grouped in blocks of 2 or 3 consecutive events, depending on the number of events in each course. If a course must be assigned 3 events, a block of three consecutive events is built, if it has 4 events, it is grouped in 2 blocks of two consecutive events and if there are 5 events a block of 2 events is created and one of 3.
Additionally, when an allocation or movement of classroom-time slot pairs is made, these should be grouped in blocks of consecutive strips. This in order to facilitate the fulfillment of the hard restriction R15.
4.3.3. Initialization of individuals
Each individual represents a solution to the problem. To create an individual, two matrices are generated, the first matrix, called chromosome which contains the information related to the events and the second matrix, called pairs classroom-time slot, which contains the combinations of classrooms and time slots as described in section 4.2.
Then, each pair classroom-time slot is assigned to each event. To accomplish this, it starts with the teachers, for each teacher a vector of assigned courses and a weekly availability vector are generated. Now, for each course around the vector, the events that have not been assigned are identified, as long as the events of a course are not assigned in their entirety, the algorithm tries to assign a random block of classroom-time slot pairs of two or three consecutive events, if possible, within the availability of the teacher.
4.3.4. Neighborhood structures
To carry out the movements within each individual, 4 neighborhood structures are used:
N1: An operator that exchanges classroom-time slot pairs already assigned to a block of events for unassigned classroom-time slot pairs.
N2: An operator that exchanges the classroom-time slot pairs of two blocks of events, of the same size, between them.
N3: An operator that exchanges the classroom-time slot pairs of three blocks of events, of the same size, with each other.
N5: An operator that takes blocks of unassigned classroom-time slot pairs that share the same fringes and exchanges them with the classroom-time slots pairs of the blocks of events that must be programmed in parallel.
4.3.5. Local search operator 1.
The Local search operator 1 (LS1) works on all the blocks of events of the solution. This algorithm works in two phases, in the first stage, it uses the structures N1, N2 and N3 to exchange blocks of events in order to obtain a feasible solution. If a feasible solution is found in this phase, the second phase is executed. The second phase operates in a similar way to the first; however, in this stage, the violations of soft restrictions are considered. In this way we seek to obtain a feasible good quality solution.
The algorithm starts by verifying the feasibility of each block of events (a block of events is infeasible if one of them violates any hard restriction). If a block is infeasible, the structures N1, N2 and N3 are applied in order to find an improvement or to reach a certain number of steps. To verify if there is an improvement, a Delta Evaluation is used, as described by the authors of the algorithm in their work. Once all the blocks are evaluated, the feasibility of the solution is calculated, if the obtained solution is still infeasible, the algorithm ends, otherwise the quality of each block of events is verified. If a block has a penalty in its quality, the structures N1, N2 and N3 are applied as previously done. Once all the blocks have been evaluated, LS1 finishes by showing a potentially improved Individual.
4.3.6. Local search operator 2
The Local Search operator 2 (LS2) tries to meet the parallelism restriction R18 by making use of the neighborhood structure N5 and makes the movements as long as there is an improvement in the aptitude of the solution.
4.3.7. Crossing operator
This operator starts by selecting two people from the solution population as parents P1 and P2 through the selection tournament method. In the crossing process, the parent P1 is initially selected, selected as the descendant. Then, for each block, a neighbor solution is created, exchanging the classroom-time slot pairs of the current descendant with parent P2 (ensuring that restrictions R5 and R15 are not violated). Finally, the descendant is updated with the classroom-time slot pairs of parent P2, if there is an improvement in the aptitude of the solution.
4.3.8. Mutation operator
The mutation operator is in charge of randomly moving each block of events with a probability Pm using the neighborhood structures N1, N2 and N3 to make the movements within the solution.
4.3.9. Room stability heuristic
If the solution generated by the GSGA phase of the algorithm fails to meet the minimums related to the stability of classrooms. This heuristic is executed to try to satisfy the soft restriction R14 as best as possible. In this case, the movements are made between rooms assigned to the same time slots, as a consequence, only the classrooms are exchanged. The procedure starts with the teachers. For each teacher, the courses assigned to him or her are identified; then for each assigned course, the time slots are identified. If there is more than one classroom assigned to these fringes, they are located in a single room and the classroom-time slot pairs of said course are blocked so that they are not exchanged in future movements. If it is not possible to assign all the fringes in a single classroom, the time slots of the course's blocks of events will be assigned and once their classrooms are linked, their classroom-time slot pairs are blocked.
4.3.10. Tabu search procedure
Once the GSGA phase of the algorithm is finished, if the obtained solution is not optimal, a tabu search heuristic operates on the best obtained solution so far. The TS algorithm makes use of the neighborhood structures N1 and N2 to generate the possible movements of the solution. Also, it considers a movement that involves an event that has moved a certain number of iterations tabu (tabu size list). In addition, it applies a variable neighborhood that randomly chooses a certain percentage of neighborhood V, defined by N1 and N2.
The algorithm ends when the defined number of iterations is completed and yields the best solution obtained so far. Finally, the Heuristic Room Stability is executed again.
5. Experimentation and analysis of results
The algorithm for the UCTP solution was programmed in the Matlab® tool in its R2107a version, while the factorial design was developed in the Minitab® 18 statistical software. Both were run on a computer with an Intel Core i7 2700 @ 3.6 GHz processor and 8 Gb of RAM.
The instances to be processed are those generated from the programming of classes of the academic periods 2018-1 and 2018-2 of the Industrial Engineering program of the UIS.
The HGATS algorithm has seven parameters that guide its performance. In order to set the parameters, a fractional design 2k-3 with 5 replicas was designed. The factors and levels considered are presented in Table 3. These values were selected from tests with the specific instance looking for the computation time to be less than 1800 seconds.
When the adjustment of the parameters is done using a fractional factorial design, it must be taken into account that, although this design allows to evaluate the performance of the algorithm with few treatments, it is possible to fall into errors due to the confusion between factors and interactions due to the low resolution of the design. Finally, the following parameters were obtained for each of the instances, which are recorded in Table 4.
5.1. Results evaluation
Table 5 shows the results of the best obtained solution after 10 runs of the Adapted HGATS algorithm and the computational time used in each instance. The obtained value (less than 1000) in the suitability of the solution shows that the solution is feasible. On the other hand, Table 6 presents in detail the penalty values associated with each described restriction in the aptitude function of section 4.2.
Regarding the computational time used, it can be classified as acceptable considering that the time dedicated exclusively to the programming of classes usually takes between 3 and 4 hours, according to the Academic Coordinator. Restrictions R2, R5, R8, R9, R10, R11 and R12 are not considered in the previous table, because these restrictions are guaranteed throughout the iteration process of the algorithm.
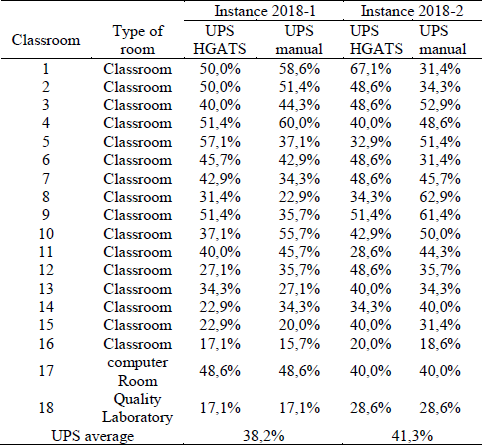
The restrictions considered within the problem are part of the current reality of the process of programming classes in EEIE, however, it is not possible to carry out a direct comparison between the proposed algorithm and the manual programming performed for the instances in question, due to the fact that the Academic Coordinator in charge, at the time, did not necessarily use these criteria during the programming time. Considering the previous situation, it is interesting to observe the obtained result in both techniques using the Weekly Percent Use (UPS) of the classrooms, applied by [1] as an indicator, without pretending to make a direct comparison between them. Table 7 summarizes the information of the indicator for each of the instances to be treated.
The UPS indicator represents the percentage of slots in which a classroom is occupied in comparison to the total slots in which it is available to be programmed during a week.
6. Conclusions
As noted in the literature review, the majority of works and research found tend to focus on the evaluation of algorithms on reference instances, so the application of these algorithms in real-world instances, such as this project, serves as reference to future research that focuses on the use of metaheuristics to solve the UCTP in educational institutions with similar conditions.
The versatility of metaheuristic techniques has expanded the possibility of finding good solutions to problems of a high level of complexity. Among these, the Genetic Algorithm and the Tabu Search Algorithm have been widely documented in the area of university schedules, which facilitates extending its application to specific problems, such as our research.
The use of a hybrid algorithm has been proposed given the advantages when balancing the ability to explore and exploit solutions during the search process.
Since the obtained schedules were feasible in all the runs made, the HGATS algorithm has proven to be effective for the proposed problem. In addition, the maximum computational time spent has not exceeded 25 minutes, which is considered a reasonable time.
The definition of parameters was made considering a Fractional Factorial Design of resolution IV, which generates confusion between the factors and interactions, however, with the parameters used, good (feasible) results were obtained in the final solutions.
The UPS indicator was defined in order to observe the way in which the allocation of classrooms is made within the programming made by HGATS. From this indicator, it can be seen that, for instance 2018-1, only 38,2% of the available spaces are used, while for instance 2018-2, this value is 41,3%. These values indicate that classrooms are not being used efficiently.
7. Recommendations
Expand the reach of the problem by including student enrollment data and the capacity of the classrooms.
Program the MILP model defined in chapter 3, using GAMS, in order to obtain the optimal solution of the problem and compare the performance of the HGATS metaheuristics with that solution.
Given that the HGATS hybrid algorithm works in separate phases, it is convenient to evaluate the performance of the Genetic Algorithm and Tabu Search independently, in order to adequately exploit the capacities of each one of them in reasonable computing times.
Due to the low average UPS in both instances it is recommended to reduce the number of classrooms available for programming. In this way, the algorithm is forced to look for good solutions, taking advantage of available classrooms better and, consequently, improving that indicator.