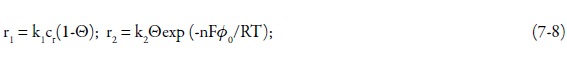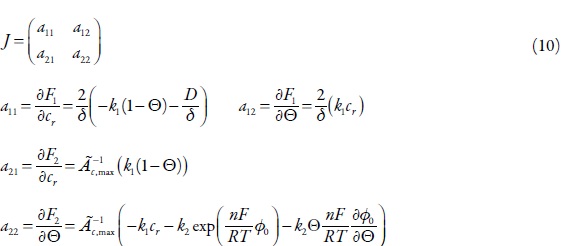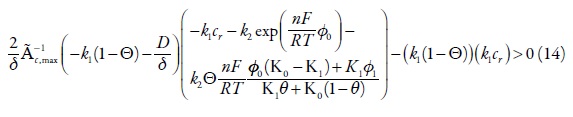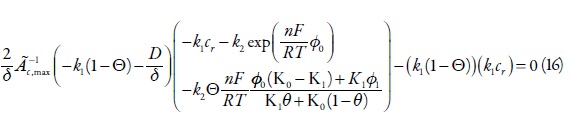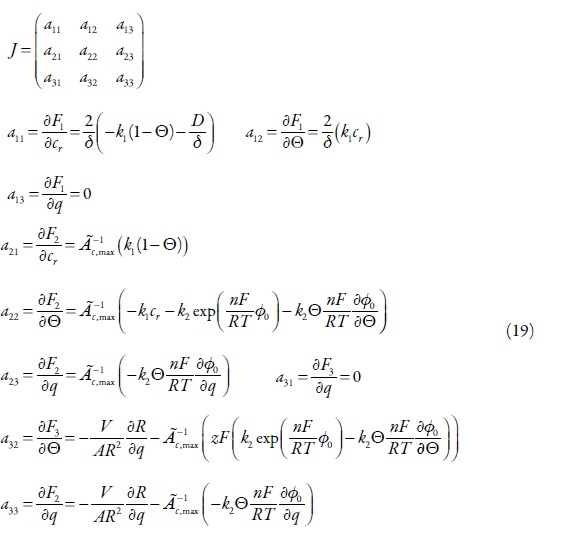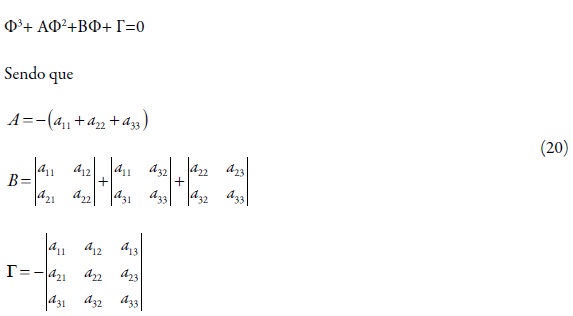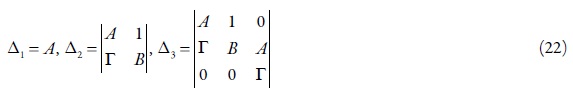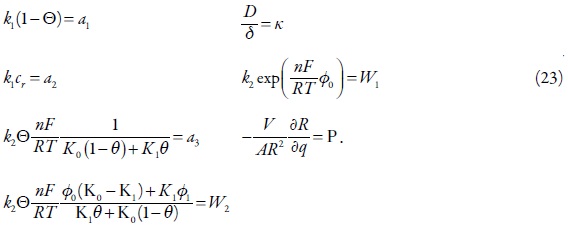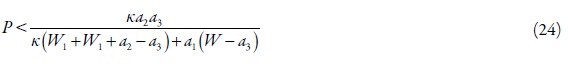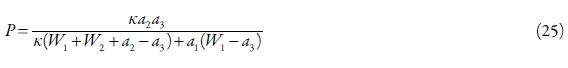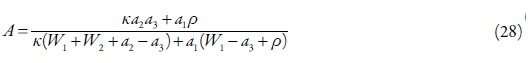Artículo de investigación

A investigação matemática do desempenho de biossensores eletroquímicos enzimáticos baseados nos polímeros condutores

The mathematical investigation of the work of enzyme biosensors based on conductive polymers

Volodymyr Valentynovych Tkach^*, Vasyl´ Vasyl´ovych Nechyporuk¹ e Petro Ivanovych Yagodynets¹

¹58012, Ucrânia, Rua Kotsyubyns´kogo, 2, Universidade Nacional de Chernivtsi,

^*E-mail do contato nightwatcher2401@gmail.com (+55 16 3351 8066)

Recibido para evaluación: 26 de noviembre de 2012.
Aceptado para publicación: 20 de diciembre de 2012.

RESUMO

O desempenho de biossensores eletroquímicos baseados em polímeros condutores (PC), modificados pelos fragmentos da enzima, foi descrito matematicamente nos modos potenciostático e potenciodinâmico de voltagem constante. Os modelos matemáticos foram analisados por meio da teoria de estabilidade linear e da análise de bifurcações. As condições da estabilidade dos estados estacionários foram inferidas com o uso dos requisitos da estabilidade do estado estacionário para os sistemas de duas dimensões (para o modo potenciostático) e usando o critério de Routh- Hurwitz (para o modo potenciodinâmico de voltagem constante). As causas das oscilações eletroquímicas, possíveis durante o funcionamento do sensor, são: a influência da oxidação eletroquímica dos redutores fortes, que se formam durante a reação específica entre o polímero e o analito, sobre a camada dupla e também a formação da forma menos condutora do polímero (para o modo potenciodinâmico). Caso a detecção se realize por meio das reações autocatalíticas, estas também são responsáveis pelo comportamento oscilatório no processo.

Palavras-chave:polímeros condutores, sensores bioquímicos, sensores enzimáticos, sensores eletroquímicos, oscilações eletroquímicas, o estado estacionário estável.

SUMMARY

The work of CP-based biosensors was described mathematically in potentiostatic and potentiodynamic mode with constant voltage was mathematically described. The mathematical models were analyzed by linear-stability theory and bifurcation analysis. The stable-state conditions were derived by using the stable-state requirements for 2-dimensional systems (for the potentiostatic mode) and Routh-Hurwitz criterion (for the potentiodynamic mode). The causes for the oscillatory behavior are the influence of the anodic oxidation of strong reducents forming during the work of the sensor and the formation of the less conductive polymer form (for the potentiodynamic mode). For the case of the presence of autocatalytic stage, its influence is the third oscillations´ cause. The causes of monotonic instability and respective critical values of parameters for potentiostatic mode were also found.

Key words: Conductive polymers, biosensors, enzymatic sensors, electrochemical sensors, electrochemical oscillations, stable steady-state.

INTRODUÇÃO

Os polímeros condutores têm sido intensamente investigados durante as quatro últimas décadas, haja vista as possibilidades de serem aplicados em várias áreas. Uma das aplicações mais importantes dos compostos heterocíclicos é na confecção de sensores e biossensores eletroquímicos capazes de determinar as substâncias diferentes.

Os polímeros condutores podem ser usados como parte dos sensores eletroquímicos, porque eles se modificam facilmente e, assim sendo, é relativamente fácil incorporar um grupo funcional, capaz de reagir especificamente com o analito. Outrossim, o sinal analítico, fornecido por eles, é facilmente interpretado. Na maioria dos casos, eles podem ser regenerados.

Contudo, as instabilidades eletroquímicas (a instabilidade oscilatória e (ou) monotônica) podem ser observadas durante a resposta de sensor [1-8]. Para prever a possibilidade delas e o mecanismo para a sua aparição, é preciso criar um modelo matemático, capaz de descrever o funcionamento deste sensor e investigá-lo, fazendo-nos mais a par do processo.

Nós já fizemos uma tentativa de descrever o desempenho deste sensor no modo galvanostático [4], como também os biossensores de outros tipos de desempenho [6-8]. O objetivo deste trabalho, então, é descrever matematicamente nos modos potenciostático e potenciodinâmico (mantendo a voltagem constante) o desempenho deste sensor.

O SENSOR E SEU MODELO MATEMÁTICO

A descrição fenomenológica do sensor a se descrever. O objeto desta investigação é o sensor eletroquímico baseado no polímero condutor, modificado pela enzima, que cobre o transdutor (sendo a placa metálica), descrito em [1-3].

Durante a ausência do analito, o polímero condutor modificado está presente na superfície do elétrodo no seu estado oxidado e a reação anódica não ocorre. Quando o analito está presente, ele começa a oxidar-se quimicamente na superfície do PC, modificado pelas enzimas. A forma oxidada, então, transforma-se na reduzida para depois voltar para o estado oxidado durante a reação eletroquímica.

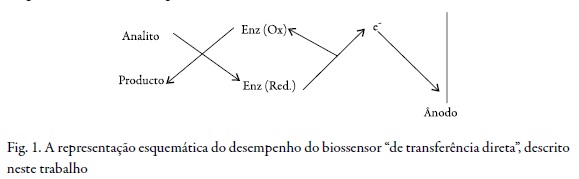
Esquematicamente, isto pode ser descrito como:

Os fragmentos da enzima são ligados ao polímero condutor pelas ligações covalentes (sendo então parte dele). O processo da reação do sensor conterá então duas etapas, conforme apresentado a seguir:

Analito + CP - Enz (ox) → CP - Enz (red) + Produto (oxidação química)

CP – Enz (red) - ne- → CP – Enz (ox) (oxidação eletroquímica)

Exemplo concreto. Um dos exemplos concretos do sensor a se descrever é o sensor amperométrico descrito no artigo [2] e na tese [5].

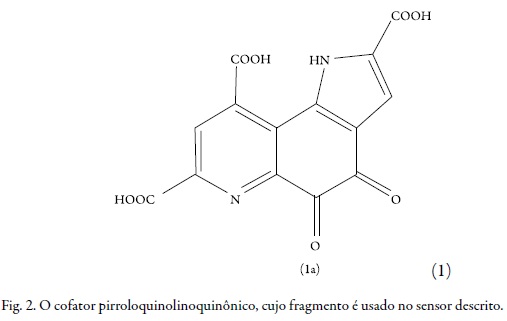
Neste caso, a enzima, cujos fragmentos são ligados com o polímero condutor, contém o cofator PQQ (pirroloquinolinoquinônico), cuja reatividade é independente da presença do oxigênio.

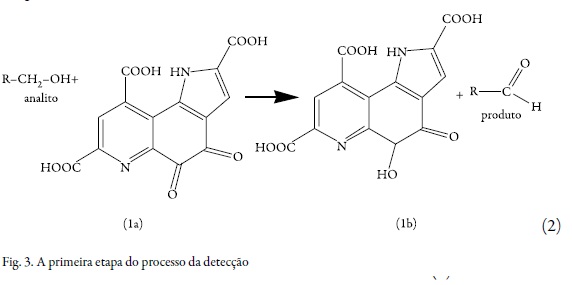
A molécula do cofator PQQ (1a) contém três anéis condensados – piridínico, substituido por dois grupos carboxílicos, orto-quinônico e o pirrólico, substituido por um grupo carboxílico. Entre eles, o anel orto-quinônico participa na transferência de prótons da molécula do analito (por exemplo, um dos álcoois). O esquema geral da reação é representado como:

Enquanto que a forma reduzida do PQQ tem o sistema conjugado rompido, na forma oxidada, este não é tal (um dos grupos carbonila do anel quinônico é parcialmente reduzido, o que quebra o sistema conjugado entre o anel piridínico e o segundo grupo carbonila).

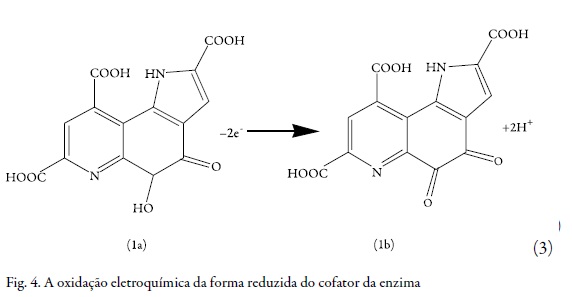
Depois, no próximo passo, a forma reduzida do PQQ é oxidada eletroquimicamente.

Geralmente, o polímero condutor, que contém o fragmento do cofator de uma enzima, pode-se sintetizar tanto pela polimerização (química ou eletroquímica [5]) do monômero específico, quanto pela copolimerização de duas espécies de monômeros.

O modo potenciostático: Para descrever matematicamente o desempenho deste sensor no modo potenciostático, vamos a introduzir duas variáveis:

C – a concentração do analito

Θ – o grau da redução dos fragmentos da enzima (neste caso, as cadeias poliméricas, que contêm a forma reduzida da enzima) são os compostos preliminares a se formarem no processo da detecção, ou seja, os compostos como (1b).

Suposições: A fim de simplificar o modelo, nós supomos que o líquido esteja agitando-se intensamente e, posto assim, podemos menosprezar a influência do fluxo da convecção, o eletrólito de suporte esteja em excesso, assim sendo, podemos menosprezar a influência do fluxo da migração. A distribuição concentracional do analito na camada da difusão é suposta a ser linear e a expessura da camada constante e igual a d. A ordem das reações é suposta a ser igual a um.

O analito na camada de difusão. O analito entra na camada pre-superficial por meio de difusão e sai dela reagindo com o polímero (ou, para ser exato, oxidando-se pelo fragmento da enzima, incorporado na cadeia polimérica). A equação do balanço da concentração pre-superficial do monômero se apresenta como:

O composto intermediário. É formado através do primeiro passo da reação e desaparece através do segundo. A equação do balanço então será descrita como

Sendo que Ã_max é a concentração superficial máxima do polímero modificado pelos grupos da enzima reduzida, r₂ é a velocidade do segundo passo da reação.

Para investigar matematicamente o desempenho deste sensor no modo potenciostático, é preciso analisar o sistema das equações (4 – 5).

As velocidades da reação química e eletroquímica podem se descrever como

Sendo k₂ a constante da reação, n a quantidade dos elétrons transferidos, F é a constante de Faraday, R significa a constante universal dos gases, T significa a temperatura absoluta do vaso e ø_o significa o salto do potencial relativamente ao potencial da carga zero.

A carga do elétrodo

K₀ e K₁ são as capacitâncias das regiões de dupla camada elétrica? que correspondem às regiões da superfície coberta pelo polímero modificado pela enzima oxidada e reduzida.

Resultados e discussão (seção 1). O comportamento deste sistema é investigado através da teoria da estabilidade linear. A matriz funcional de Jacobi deste sistema se vê como:

Os elementos desta matriz, calculados para o estado estacionário, são:

Sendo que:

Os "valores próprios" desta matriz podem ser descritos como:

As condições do estado estacionário descrevem-se como Tr J<0, Det J>0

As condições da instabilidade oscilatória (bifurcação de Hopf ) são Tr J=0, Det J>0.

As condições da instabilidade monotônica (bifurcação de sela e nó) são Tr J <0, Det J = 0.

As condições do estado estacionário estável. A condição Tr J <0 implementar-se-á com certeza se ø₀ for positivo. Isso ocorre durante a oxidação do redutor fraco ou da meia força. Mesmo que ø₀ seja negativo ou igual ao zero, esta condição vai ser implementada na região vasta dos valores de parâmetros. Para o sensor amperométrico, esta região de parâmetros corresponde à região, em que a dependência I(c) é linear (sendo a região do melhor desempenho).

A condição Det J >0 também será implementada, com certeza, sob as condições mencionadas acima.

As condições do comportamento oscilatório. A condição Tr J=0 implementa-se, caso a diagonal principal da matriz de Jacobi contenha as parcelas positivas. A única parcela capaz de ser positiva é a

Ela é positiva se ø₀ for negativo. Isso ocorre durante a oxidação anódica dos redutores fortes que surgem durante o funcionamento do sensor, neste caso, é a forma reduzida. Como os potenciais dos pares de oxidação e redução da reação 1 e 2 são de valores próximos, pode-se afirmar que o comportamento oscilatório será realizado, se o analito for redutor forte. Esta condição é a mesma que no modo galvanostático [4].

As condições da instabilidade monotônica. A instabilidade monotônica ocorre nas condições da bifurcação de sela e nó. A condição Det = 0 pode-se descrever como

Esta instabilidade pode ser realizada durante a oxidação anódica dos redutores de meia força. Nestas condições, o sistema está em um de muitos estados estacionários, sendo cada instável.

O modo potenciodinâmico da voltagem constante. Neste modo, o comportamento do sensor é mais complicado e a análise dele denota-o. Sendo assim, as condições de instabilidade e da bifurcação de sela e nó são diferentes. Outrossim e o comportamento oscilatório é causado por mais um fator.

A fim de descrever o comportamento eletroquímico deste sistema, nós introduzimos três variáveis:

C – a concentração do analito;

Θ – o grau da redução dos fragmentos da enzima;

q – a carga do elétrodo;

supondo o suposto acima.

O sistema de equações do balanço para este sistema descrever-se-á como

Sendo V a voltagem, A a área do elétrodo, R a resistência do elétrodo.

Resultados e discussão (para o modo potenciodinámico).

O estado estacionário estável. Para determinar as condições do estado estacionário estável, vamos usar o critério de Routh e Hurwitz. A equação caraterística do sistema de equações (1-3) pode ser descrita como

Sendo que

O critério de Routh e Hurwitz requer que, para um estado estacionário estável, os menores dos membros da diagonal principal da matriz de Hurwitz:

Visto que Δ₃= Γ Δ₂, podemos formar a condição do estado estacionário estável como C>0.

Para simplificar a análise do determinante da matriz, introduzimos novas variáveis

Haja vista a introdução das novas variáveis e a condição Γ>0, obter-se-á o valor crítico do parâmetro da resistência da superfície P, servindo de "margem de estabilidade" dos estados estacionários

Neste valor crítico, segundo a condição Γ=0, ocorre a instabilidade monotônica.

A instabilidade oscilatória. Para ela ser realizada, é obrigatório que a diagonal principal da matriz contenha as parcelas positivas (as quais descrevem a positiva ligação de retorno).

Influência da etapa autocatalítica

Pode-se ver que a primeira causa do comportamento oscilatório, mencionada acima, é também válida para este sistema. Todavia, há mais uma causa deste comportamento. Se o composto a se formar durante a oxidação for menos condutor e não puder depor carga elétrica, a resistência do elétrodo aumenta e o valor de carga do elétrodo diminui (ou seja, realiza-se aparição do polímero apassivador). Isso se manifesta no caso de A > 0.

Para o caso da presença da etapa autocatalítica no processo, o modelo aparece alterado, sendo as alterações,

1) Outra equação para a velocidade da reação na primeira etapa

2) Modificados os elementos da diagonal principal da matriz, aparece a nova variável

3) Modificadas as condições da estabilidade de estado estacionário e bifurcação estática (de sela e nó)

4) Aparece mais uma causa do comportamento oscilatório.

O mesmo modelo pode, além dos sensores enzimáticos, descrever também o funcionamento dos imunobiossensores (contendo o PC a substância ativa do anticorpo), como também os biossensores específicos de detecção das consequências complementares do ADN e os sensores eletroquímicos sem uso de biossubstâncias.

O mesmo modelo é capaz de descrever o processo da modificação do polímero condutor, consistente numa etapa química e numa eletroquímica, sendo o desempenho de sensores o caso particular.

CONCLUSÕES

1. O desempenho analítico de sensores eletroquímicos enzimáticos baseados nos polímeros condutores foi descrito, matematicamente, através da teoria da estabilidade linear e da análise de bifurcações.

2. É mostrado que, no modo potenciostático, as causas do comportamento oscilatório são as mesmas que no galvanostático. A região dos estados estacionários estáveis é muito vasta para usar este sensor nas finaldades

3. É mostrado que no modo potenciodinâmico (da voltagem constante) tem mais uma causa do comportamento oscilatório. É a possível formação do polímero menos condutor durante a oxidação anôdica (ou seja se a forma oxidada do mediador for menos condutiva que a reduzida.

4. Para o sistema com a reação autocatalítica, o comportamento é um pouco mais complicado. A terceira causa do comportamento oscilatório, para o caso, é a formação autocatalítica da forma reduzida do polímero.

5. Temos estrutura dissipativa, cuja existência é mantida pela presença do analito na solução.

REFERÊNCIAS

1. V.M. de Andrade, "Confecção de biossensores através da imobilização de biocomponentes por eletropolimerização de pirrol", Tés. M. Eng. UFRS, Porto Alegre, 2006.         [ Links ]

2. A. Ramanavicius, A. Ramanaviciene, A. Malinauskas, Electrochemical sensors based on conducting polymer—polypyrrole, Electrochim. Acta, 51, 6025-6037 (2006)        [ Links ]

3. T. McQuade, A. Pullen, T.M. Swager, Conjugated polymer based chemical sensors, Chem. Rev. 100, 2537-2574 (2000)        [ Links ]

4. V. Tkach, V. Nechyporuk, P. Yagodynets´, Abstract 7^th Nanoscience and Nanotechnology conference, Istanbul, 2011, p. 173.         [ Links ]

5. J.P. Tosar-Rovira, Estudio de la inmovilización de oligonucleótidos a elétrodos modificados de oro : polipirrol, y detección electroquímica de secuencias complementarias, Tes. Lic. Bioquím., Universidade de la República, Montevideo, 2008.         [ Links ]

6. V.V. Tkach, V.V. Nechyporuk, P.I. Yagodynets´, Yu.V. Meslyuk, Mathematical model of the work of the mediated conducting polymer sensors with the use of the polymers of heterocyclic compounds, Rev. Soc. Quím. Perú, 77, 259-266 (2011).         [ Links ]

7. V.V. Tkach, V.V. Nechyporuk, P.I. Yagodynets, Yu.V. Meslyuk, 2^nd International Conference "Advances in Heterocyclic Chemistry, 25-27^th" of September 2011, Tbilisi, Georgia, p. 101-102.         [ Links ]

8. V. Tkach, V. Nechyporuk, P. Yagodynets´, I. Rusnak, The CP-based electrochemical biosensors with autocatalytic stage in their function and the mathematical description of their work, Orbital Elec. J. Chem., 4, 136-145 (2012).         [ Links ]