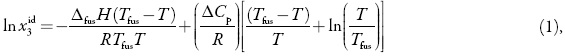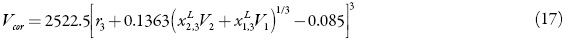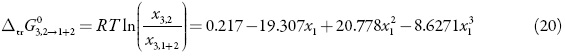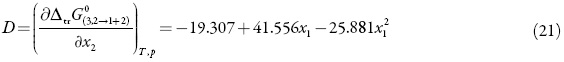Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Colombiana de Ciencias Químico - Farmacéuticas
Print version ISSN 0034-7418
Rev. colomb. cienc. quim. farm. vol.45 no.2 Bogotá May/Aug. 2016
https://doi.org/10.15446/rcciquifa.v45n2.59941
http://dx.doi.org/10.15446/rcciquifa.v45n2.59941
Solution thermodynamics and preferential solvation of 3-chloro-N-phenyl-phthalimide in acetone + methanol mixtures
Termodinámica de soluciones y solvatación preferencial de 3-cloro-N-fenil-ftalimida en mezclas acetona + metanol
Grecia Angeline del Mar Areiza Aldana1, Aleida Cuellar Lozano1, Nasly Alexandra Peña Carmona1, Diego Iván Caviedes Rubio1, Abbas Mehrdad2, Amir Hossein Miri2, Gerson Andrés Rodríguez Rodríguez3, Daniel Ricardo Delgado1*
1 Programa de Ingeniería Industrial, Universidad Cooperativa de Colombia, Neiva, Colombia.
2 Department of Physical Chemistry, Faculty of Chemistry, University of Tabriz, Tabriz, Iran.
3 Grupo de Investigaciones Farmacéutico-fisicoquímicas, Departamento de Farmacia, Facultad de Ciencias, Universidad Nacional de Colombia, Sede Bogotá, Cra 30 N. ° 45-03, Bogotá D.C., Colombia.
* E-mail: danielr.delgado@campusucc.edu.co
Received: June 8, 2016 Accepted: June 23, 2016
Summary
The thermodynamic properties of the 3-chloro-N-phenyl-phthalimide in acetone + methanol cosolvent mixtures were obtained from solubility data report in literature. The solubility was higher in near acetone and lower in pure methanol at all temperatures studied. A non-linear plot of ∆solnH° vs. ∆solnG° shows a negative slope from pure acetone up to x1 = 0.691. Beyond this composition, a variable positive slope is obtained with the exception of mixtures with x1 = 0.121, x1 = 0.272 and x1 = 0.356 which is a not common trend in these systems. The preferential solvation of 3-chloro-N-phenyl-phthalimide by the components of the solvents was estimated by means of the inverse Kirkwood–Buff integral method, showing the 3-chloro-Nphenyl-phthalimide is preferential solvated by methanol in more polar mixtures and by acetone in less polar ones.
Keywords: 3-Chloro-N-phenylphthalimide, solubility, solution thermodynamics, activity coefficients, preferential solvation.
Resumen
Las propiedades termodinámicas de 3-cloro-N-fenil-ftalimida en mezclas cosolventes acetona + metanol fueron obtenidas a partir de los datos de solubilidad reportados en la literatura. La mayor solubilidad se presentó en acetona y la menor en metanol puro en todas las temperaturas estudiadas. La grafica ΔsolnH° vs. ΔsolnG° presenta una tendencia no lineal, con una pendiente negativa desde la acetona pura hasta x1 = 0,691 a partir de esta composición hasta el metanol puro se obtiene una pendiente positiva variable con la excepción de las mezclas con x1 = 0,121, x1 = 0,272 y x1 = 0,356, la cual es una tendencia poco común en estos sistemas. La solvatación preferencial de 3-cloro-N-fenil-ftalimida por cada uno de los solventes de la mezcla se estimó por medio del método de las integrales inversas de Kirkwood-Buff mostrando que la 3-cloro-N-fenil-ftalimida se solvata preferencialmente por metanol en las mezclas más polares y por acetona en las menos polares.
Palabras clave: 3-cloro-N-fenil-ftalimida, solubilidad, termodinámica de soluciones, coeficiente de actividad, solvatación preferencial.
Introduction
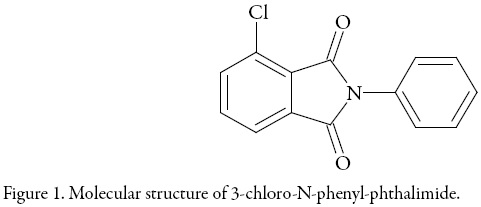
3-chloro-N-phenyl-phthalimide (Fig. 1) (Synonyms: 4-chloro-2-phenyl-isoindoline1,3-dione; 4-Chloro-2 phenyl-isoindolin-1,3-dion; 3-Chloro-N-phenyl-phthalimid; 4-chloro-2-phenyl-isoindole-1,3-dione; 3-chloro-N-phenyl-phthalimide) is an interesting compound because of its use in the synthesis of 3,3'-bis(N-phenylphthalimide) and 2,2',3,3'-diphenylthioether dianhydride, which are monomers for the preparation of polyimide, and those synthetic routes require a high purity 3-chloro-N-phenylphthalimide [1].
Knowledge of thermodynamic properties and preferential solvation is important in order to optimize synthesis processes like aforementioned [2]. For this reason, the purpose of this study is to evaluate the effect of the co-solvent composition on solubility, solution thermodynamics and preferential solvation of 3-chloro-N-phenyl-phthalimide in binary mixtures of acetone and methanol. The temperature dependence of the solubility allows a thermodynamic analysis that permits insight into the molecular mechanisms involved in the solution processes. The other hand, the estimate of the preferential solvation of the solute by the components of the solvent mixture, it is performed by the application of the inverse Kirkwood-Buff integral (IKBI) method [3-5].
Theoretical
Ideal solubility
The ideal solubility as a function of temperature can be calculated by using the following equation:
here x3id is the ideal solubility of the solute as mole fraction, ∆fusH is the molarenthalpy of fusion of the pure solute (at the melting point), Tfus is the absolute melting point, T is the absolute solution temperature, R is the gas constant (8.314 J mol–1 K–1), and ∆Cp is the difference between the molar heat capacity of the crystalline form and the molar heat capacity of the hypothetical super-cooled liquid form, both at the solution temperature [6]. Since ∆Cp cannot be easy experimentally determined it is usual assuming that it may be approximated to the entropy of fusion, ∆fusS [7].
Activity coefficients
The activity coefficients γ3, were calculated as x3id/x3 where x3 is the experimental solubility. From γ3 values a rough estimate of solute-solvent intermolecular interactions can be made by considering the following expression [8]:
where e11, e33 and e13 represent the solvent-solvent, solute-solute and solvent-solute interaction energies, respectively, the first two terms are unfavorable for solubility and the third term favors the solution process; V3 is the molar volume of the super-cooled liquid solute and φ1 is the volume fraction of the solvent. As reported in the literature, for relatively low solubilities x3, the term V3φ12/RT may be considered constant; thus, γ3 depends mainly on e11, e33 and e13 [9]. The contribution of the e33 term could be considered as constant in all mixtures [10].
Thermodynamic functions of solution
Apparent standard enthalpy change of solution is obtained from the Eq. (4) by using the mean harmonic temperature (Thm) [calculated as:Thm = 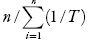 ], where n is the number of temperatures studied [4].
], where n is the number of temperatures studied [4].

The apparent standard Gibbs energy change for the solution process (∆solnG°), considering the approach proposed by Krug et al. [11], is calculated at Thm by means of:
where the intercept is obtained from the treatment of ln x3 as a function of 1/T – 1/Thm. Finally, the standard apparent entropy change for solution process (∆solnS°) is obtained from the respective ∆solnH° and ∆solnG° values at Thm by using:
the relative contributions by enthalpy (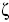 H) and entropy (
H) and entropy ( TS) toward the solution process are given by equations 7 and 8 [12-13].
TS) toward the solution process are given by equations 7 and 8 [12-13].
Preferential solvation
The KBIs are given by the following expressions:
here g1,3 is the pair correlation function for molecules of solvent 1 in the 1 + 2 mixtures around the solute 3, r is the distance between the centers of molecules 3 and 1, and rcor is a correlation distance for which g13(r > rcor)≈1. Thus, for all distances r > rcor up to infinite, the value of the integral is essentially zero. So, the results are expressed in terms of the preferential solvation parameter, δx1,3, for the solute 3 by the component solvents 1 and 2 [5, 14].
Where x1 is the mole fraction of 1 in the bulk solvent mixture and xL 1,3 is the difference between the local mole fraction of 1 in the near environment of the solute. If δx1,3 > 0 then 3 is preferentially solvated by 1, else by 2, within the correlation volume Vcor = (4π/3)rcor 3, and the bulk mole fraction of 1, x1. Values of δx1,3 are obtainable from those of G1,3, and these, in turn from thermodynamic data for the solvent mixture with the solute in it as shown below [6, 15].
Algebraic manipulation of expressions presented by Newman [16] leads to expressions for the Kirkwood-Buff integrals (in cm3 mol-1) for the individual solvent components 1 and 2 in terms of thermodynamic quantities [3, 6-7]:
Where KT is the isothermal compressibility of the solvent mixtures 1+2 (in GPa-1), V1 and V2 are the partial molar solvent volumes in the mixture, and V3 is the standard partial molar volume of solute in this mixture (in cm3 mol-1). The function D is the derivative of the standard molar transfer Gibbs energies of 3 with respect to the solvent composition and the function Q involves the second derivative of the excess molar Gibbs energy of mixing of the two solvents, GE 1,2, with respect to the solvent composition (in kJ mol−1, as is RT)[17]:
Because of the dependence of KT on composition this term is not known for all the systems investigated. Moreover, due to the small contribution of RT KT to the IKBI, the dependence of χT on composition will be approximated by [18-19]:
where xi is the volume fraction of component i in solution and K0T,i is the isothermal compressibility of the pure component i.
Ben-Naim [20] showed that the preferential solvation parameter can be calculated from the Kirkwood-Buff integrals as follows:
The correlation volume, Vcor, is obtained by means of the following expression proposed by Marcus [21]:
Where r3 is the radius of the solute (in nm), calculated as
However, the correlation volume requires iteration, because it depends on the local mole fractions [14].
Results and discussion
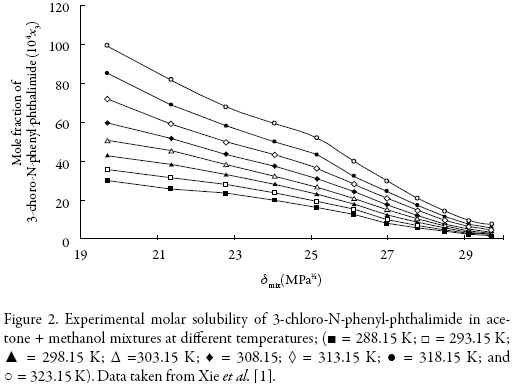
The solubility of 3-chloro-N-phenyl-phthalimide (3) in acetone (1) + methanol (2) mixtures (Fig. 2) was taken from the literature [1].
The solubility increases with temperature in all cases indicating that the dissolution process is endothermic. The highest solubility of 3-chloro-N-phenyl-phthalimide expressed as a mole fraction were obtained in near acetone at T = 323.15 K, whereas the lowest values were found in pure methanol (2) at 288.15 K (Fig. 2).
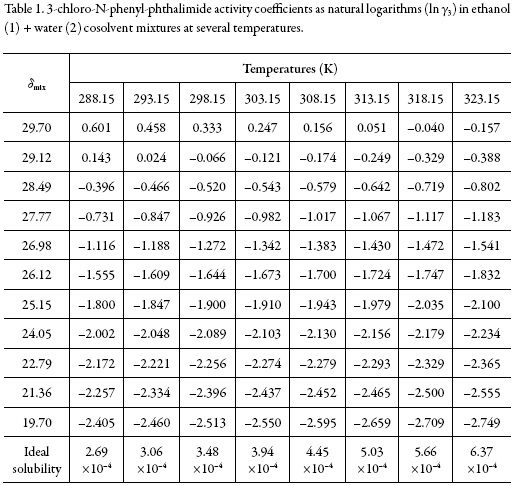
Table 1 shows the ideal solubilities expressed as a mole fraction of the solutes (x3 id) calculated by using Eq. (1) with the temperature and heat of fusion of 3-chloro-N-phenylphthalimide taken from literature, i.e. Tfus = 466.05 K and ∆fusH = 29.14 kJ mol–1 [22].
On the other hand, Fig. 2 shows the solubility profiles as a function of the polarity of the mixtures, expressed by their solubility parameters (δmix). For a binary mixture δmix is calculated from the solubility parameters of the pure solvents (δ1 = 19.6 MPa1/2 and δ2 = 29.78 MPa1/2 [23]).
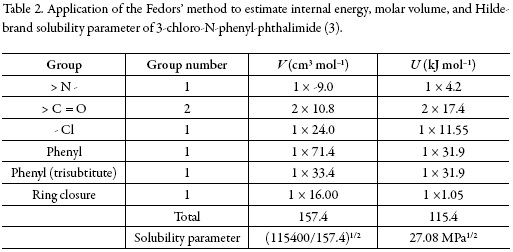
The solubility parameter of solute, estimated according to the groups contribution method proposed by Fedors [24], is δ3 = 27.08 MPa1/2 (Table 2), which is higher than the experimental value obtained (δ3 ≤ 27.08 MPa1/2). This indicates that the actual polarity of solute is lower than the expected from the additive contribution of its groups, which is lower than the experimental value [25].
The activity coefficients of 3-chloro-N-phenyl-phthalimide expressed as natural logarithms are also shown in Table 1. These values were calculated from experimental solubility was taken from Xie et al. (2016) [1]) and ideal solubility data (table 1). In the vast majority of cases, γ3 values were lower than unit (negative logarithmic values) due to the experimental solubilities are greater than the ideal ones in those cosolvent systems (acetone-rich mixtures).
As a qualitative approach, the following analysis could be made based on the energetic quantities and magnitudes described in the Eq. (2): The term e11 is highest in neat methanol and methanol-rich mixtures having larger γ3 values (0.855-1.825) which implies higher e11 and lower e13 values. On the other hand, in intermediate composition mixtures and acetone-rich mixtures (having γ3 values <1), the e11 values are relatively low but the e13 values could not to be so high. Accordingly, the solvation of 3-chloro-N-phenyl-phthalimide could be just a little higher in acetone-rich mixtures.
Thermodynamic functions of solution
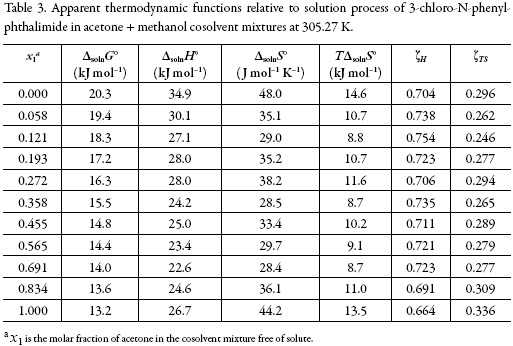
From the solubility data, the thermodynamic functions in solution are calculated (Table 3). Over the range of temperatures studied (288.15 to 323.15 K) the heat capacity change of solution may be assumed to be constant, hence ΔsolnH° should be valid for the mean harmonic temperature, Thm = 305.27 K.
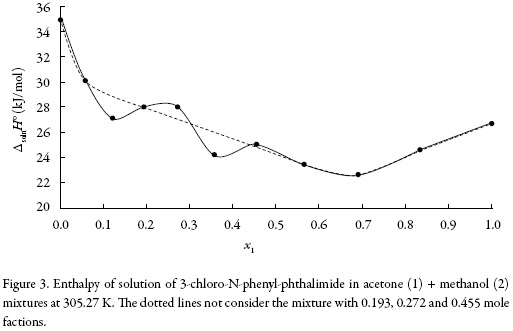
The standard Gibbs free energy of solution is positive in all cases as is the enthalpy of solution; therefore the process is always endothermic. Figure 3 shows the change of enthalpy versus the mole fraction of acetone. The decreasing enthalpy between pure methanol up to the mixture with x1 = 0.121 indicates that solubility is favored for enthalpy in these mixtures. Besides, from the mixture with x1 = 0.121 up to the mixture with x1 = 0.565 the enthalpy of solution tends to increase and then decrease, for this reason it is not possible to identify the thermodynamics properties driving the solution process. Finally, between the mixture x1 = 0.691 and the pure acetone, the enthalpy increases.
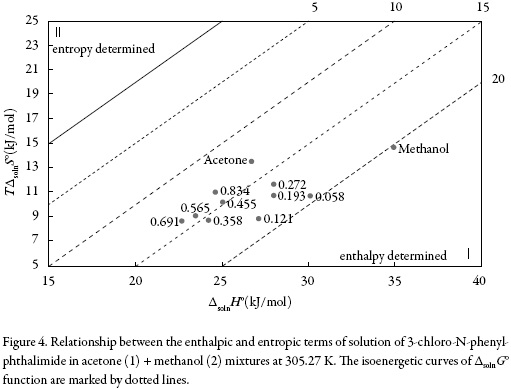
The main contributor to the (positive) standard molar Gibbs energy of solution of 3-chloro-N-phenyl-phthalimide, in all cases, is the (positive) enthalpy (ζH > 0.754). The experimental data of thermodynamic functions of solution are collected in Fig. 4. The regions where (ΔtrH° > TΔtrS° > 0) ≡ sector I; corresponds to enthalpy determined processes [4, 26-27], which is proposed by the equations 7 and 8.
Thermodynamic functions of transfer
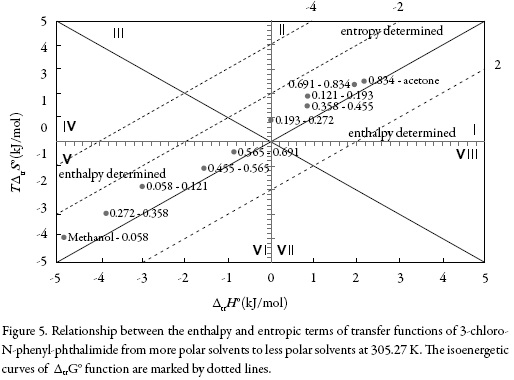
In order to verify the effect of co-solvent composition on the thermodynamic function driving the solution process, Fig. 5 collects the thermodynamic functions of transfer of 3-chloro-N-phenyl-phthalimide (3) from the more polar solvents to the less polar ones. These new functions were calculated as the differences between the thermodynamic quantities of solution obtained in the less polar mixtures and the more polar ones, by means of:
Where ∆solnF° represents the thermodynamic functions (∆solnG°, ∆solnH° or ∆solnS°). This procedure is the same followed previously in other studies reported by Holguín et al. and Delgado et al. [28-29].
Theregionswhere(ΔtrH°>TΔtrS°>0)≡sector I;(ΔtrH°<0;TtrΔS°>0;∣ΔtrH°∣>∣TtrΔS°∣) ≡sector IV and (ΔtrH° < 0; TΔtrS° < 0; ∣ΔtrH°∣ >∣TΔtrS°∣) ≡ sector V corresponds to enthalpy determined processes. The regions of the diagram where (TΔtrS° > ΔtrH° > 0)≡ sector II correspond to entropy determined processes [4, 26-27]. A schematic depiction of these relationships is given in figure 5.
So, the process of transfer in acetone-rich mixtures may indicate that the 3-chloro-Nphenyl-phthalimide molecule interacts more strongly with the acetone, however in all cases, the behavior is very random.
Enthalpy-entropy compensation of 3-chloro-N-phenyl-phthalimide
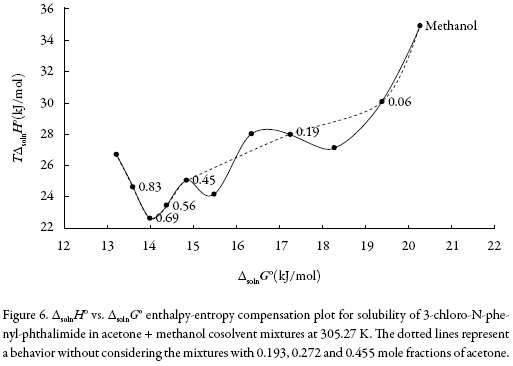
There are several reports in the literature that have demonstrated enthalpy-entropy compensation effects for the solubility of drugs in aqueous co-solvent mixtures. This analysis has been used in order to identify the mechanism of the co-solvent action. Weighted graphs of ΔsolnH° as a function of ΔsolnG° at the mean temperature allow such an analysis [30-31].
Figure 6 shows that 3-chloro-N-phenyl-phthalimide (3) in the acetone (1) + methanol (2) solvent system presents a non-linear behavior of ΔsolnH° vs. ΔsolnG° with a variable negative slope from pure acetone up to x1 = 0.691. Beyond this composition a variable positive slope is obtained with exception of mixtures with x1 = 0.12, x1 = 0.272 and x1 = 0.36, showing a non-common trend in these systems. Accordingly, the driving mechanism for solubility is the entropy in the former case, whereas in the latter case the driving mechanism is the enthalpy, probably due to better solvation of the 3-chloro-Nphenyl-phthalimide by acetone molecules.
Preferential solvation
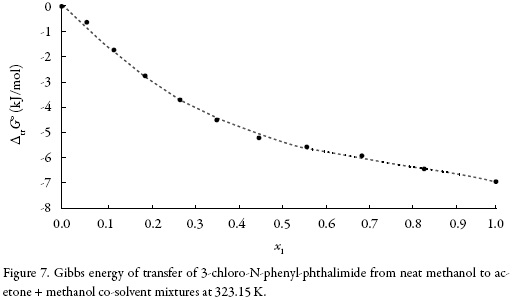
Standard molar Gibbs energy of transfer of 3-chloro-N-phenyl-phthalimide from neat methanol to acetone + methanol mixtures is calculated and correlated to a third grade polynomial from the drug solubility data by using equation (13). Figure 7 shows the Gibbs energy of transfer behavior at 323.15 K.
Thus, D values are calculated from the first derivative of polynomial models (Eq. 20) solved according to the co-solvent mixtures composition. This procedure was done varying by 0.05 in mole fraction of methanol but in the following tables the respective values are reported varying only by 0.10.
In order to calculate the Q values the excess molar Gibbs energies of mixing GExc1,2 at 323.15 Kwere used as is reported by Marcus [18], the isothermal compressibility (KT ) is given,asagoodapproximation,bythelinearexpression:x1 KT1+x2 KT2(KT1 =1,324GPa-1; (KT2 = 1.248 GPa-1) [21] and the partial molar volumes can be replaced by the molar volumes of the pure substances [32-34].
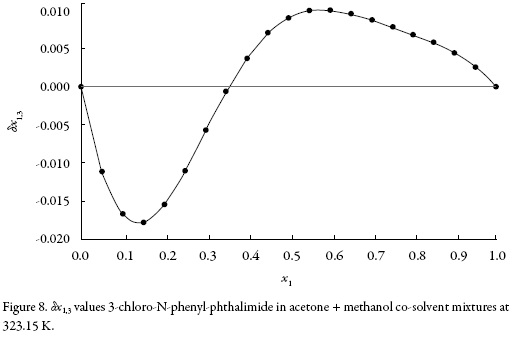
The application of the IKBI method with the gyration radius r = 0.397 nm leads to the preferential solvation parameter, δx1,3 for acetone around 3-chloro-N-phenylphthalimide which is shown in Fig. 8 at 323.15 K. The values of δx1,3 vary non-linearly with the proportion of acetone in the alcoholic mixtures (figure 8). The addition of acetone to methanol causes a negative change in δx1,3 from pure methanol up to the 0.35 in molar fraction of acetone reaching minimum values near to – 0.018 at 0.15 in molar fraction of acetone at 323.15 K. In this composition, methanol is preferred over acetone around the 3-chloro-N-phenyl-phthalimide.
The local mole fractions of methanol are greater than those of acetone from pure methanol up to 0.35 mole fractions of acetone and minors beyond this up to pure acetone. From the preferential solvation results, it may be conjectured that, in intermediate compositions and in acetone-rich mixtures, 3-chloro-N-phenyl-phthalimide is acting as a Lewis base with acetone molecules because it is more acid than methanol (the Kamlet–Taft hydrogen bond acceptor parameters are β = 0.66 for methanol and 0.507 for acetone [35]).
Conclusions
From this work it can be concluded that the solution process of 3-chloro-N-phenylphthalimide (3) in acetone (1) + methanol (2) mixtures is endothermic. A nonlinear enthalpy–entropy compensation was found for this solute in this solvent system. In this context, entropy-driving was found for the solution process in rich-acetone mixtures, whereas, for mixtures methanol-rich enthalpy-driving was found. On the other hand, 3-chloro-N-phenyl-phthalimide is preferentially solvated for methanol in mixtures more polar and preferentially solvated for acetone in minus polar ones.
Disclosure statement
No potential conflict of interest was reported by the authors.
References
1. Y. Xie, H. Shi, C. Du, Y. Cong, J. Wang, H. Zhao, Thermodynamic models for determination of 3-chloro-N-phenylphthalimide solubility in binary solvent mixtures of (acetone, ethyl acetate or 1,4-dioxane + methanol), J. Chem. Thermodyn., 100, 22 (2016). [ Links ]
2. D.R. Delgado, F. Martínez, M.A.A. Fakhree, A. Jouyban, Volumetric properties of the glycerol formal+ water cosolvent system and correlation with the Jouyban-Acree model, Phys. Chem. Liq., 50, 284 (2012). [ Links ]
3. D.R. Delgado, M.A. Peña, F. Martínez, Preferential Solvation of some sulfonamides in propylene glycol + water solvent mixtures according to the IKBI and QLQC methods, J. Solution Chem., 43, 360 (2014). [ Links ]
4. D.I. Caviedes Rubio, G.A. Rodríguez-Rodríguez, D.R. Delgado, Thermodynamic study of the solubility of naproxen in some 2-propanol + water mixtures, Revista Fac. Ciencias B., 12, 48 (2016). [ Links ]
5. D.I. Caviedes Rubio, R.G. Sotomayor, D.R. Delgado, Solvatación preferencial de la naringina en mezclas cosolventes etanol + agua mediante el método de las integrales inversas de Kirkwood-Buff, Rev. Colomb. Cienc. Quím. Farm., 44, 220 (2015). [ Links ]
6. D.R. Delgado, O.A. Almanza, F. Martínez, M.A. Peña, A. Jouyban, W.E. Acree Jr., Solution thermodynamics and preferential solvation of sulfamethazine in (methanol + water) mixtures, J. Chem. Thermodyn., 97, 264 (2016). [ Links ]
7. D.R. Delgado, G.A. Rodríguez, F. Martínez, Thermodynamic study of the solubility of sulfapyridine in some ethanol + water mixtures, J. Mol. Liq., 177, 156 (2013). [ Links ]
8. D.R. Delgado, F. Martínez, Solution thermodynamics of sulfadiazine in some ethanol+ water mixtures, J. Mol. Liq., 187, 99 (2013). [ Links ]
9. D.R. Delgado, F. Martínez, Solubility and preferential solvation of sulfadiazine in methanol+ water mixtures at several temperatures, Fluid Phase Equilib., 379, 128 (2014). [ Links ]
10. D.R. Delgado, F. Martínez, Solubility and preferential solvation of sulfamerazine in methanol + water mixtures at several temperatures, J. Solution Chem., 44, 360 (2015). [ Links ]
11. R.R. Krug, W.G. Hunter, R.A. Grieger, Enthalpy-entropy compensation. 2. Separation of the chemical from the statistical effect, J. Phys. Chem., 80, 2341 (1976). [ Links ]
12. D.R. Delgado, E.F. Vargas, F. Martínez, Thermodynamic study of the solubility of procaine HCl in some ethanol + water cosolvent mixtures, J. Chem. Eng. Data, 55, 2900 (2010). [ Links ]
13. D.R. Delgado, A. Romdhani, F. Martínez, Solubility of sulfamethizole in some propylene glycol + water mixtures at several temperatures, Fluid Phase Equilib., 322, 113 (2012). [ Links ]
14. D.R. Delgado, E.F. Vargas, F. Martínez, Preferential solvation of xylitol in ethanol + water solvent mixtures according to the IKBI and QLQC methods, Rev. Colomb. Quím., 42, 59 (2013). [ Links ]
15. D.R. Delgado, F. Martínez, Preferential solvation of sulfadiazine, sulfamerazine and sulfamethazine in ethanol + water solvent mixtures according to the IKBI method, J. Mol. Liq., 193, 152 (2014). [ Links ]
16. K.E. Newman, Kirkwood-Buff solution theory: derivation and applications, Chem. Soc. Rev., 23, 31 (1994). [ Links ]
17. J.A. Lasso, D.I. Caviedes, D.R. Delgado, Preferential solvation of 4-hydroxy-2,5dimethyl-3(2H)-furanone (DMHF) in ethanol + water mixtures according to IKBI and QLQC methods, Ingeniería y Región, 13, 139 (2015). [ Links ]
18. Y. Marcus, On the preferential solvation of drugs and PAHs in binary solvent mixtures, J. Mol. Liq., 140, 61 (2008). [ Links ]
19. M.Á Peña, D.R. Delgado, F. Martínez, Preferential solvation of indomethacin in some aqueous co-solvent mixtures, Chem. Eng. Commun., 203, 619 (2016). [ Links ]
20. A. Ben-Naim, Preferential solvation in two- and in three-component systems, Cell Biophys., 12, 255 (1988). [ Links ]
21. Y. Marcus, "Solvent mixtures: properties and selective solvation", Marcel Dekker, Inc., New York, 2002. [ Links ]
22. C. Du, R. Xu, S. Han, J. Xu, L. Meng, J. Wang, H. Zhao, Solubility of 3-choroN-phenyl-phthalimide, J. Chem. Thermodyn., 96, 187 (2016). [ Links ]
23. R.F. Fedors, A method for estimating both the solubility parameters and molar volumes of liquids, Polym. Eng. Sci., 14, 147 (1974). [ Links ]
24. A.F.M. Barton, "Handbook of solubility parameters and other cohesion parameter", 2nd edition, CRC Press, Inc., New York, 1991. [ Links ]
25. D.R. Delgado, F. Martínez, Solubility and solution thermodynamics of sulfamerazine and sulfamethazine in some ethanol + water mixtures, Fluid Phase Equilib., 360, 88 (2013). [ Links ]
26. G.L. Perlovic, S.V. Kurkov, A.N. Kinchin, A. Bauer-Brandl, Thermodynamics of solutions III: comparison of the solvation of (+)-naproxen with other NSAIDs, Eur. J. Pharm. Biopharm., 57, 411 (2004). [ Links ]
27. G.L. Perlovic, N.N. Strakhova, V.P. Kazachenko, T.V. Volkova, V.V. Tkachev, K.J. Schaper, O.A. Raevsky, Sulfonamides as a subject to study molecular interactions in crystals and solutions: Sublimation, solubility, solvation, distribution and crystal structure, Int. J. Pharm., 349, 300 (2008). [ Links ]
28. D.R. Delgado, M.A. Ruidiaz, S.M. Gómez, M. Gantiva, F. Martínez, Thermodynamic study of the solubility of sodium naproxen in some ethanol + water mixtures, Quim. Nova, 33, 1923 (2010). [ Links ]
29. A.R. Holguín, D.R. Delgado, F. Martínez, Thermodynamic study of the solubility of triclocarban in ethanol + propylene glycol mixtures, Quim. Nova, 35, 280 (2012). [ Links ]
30. P. Bustamante, S. Romero, A. Peña, B. Escalera, A. Reillo, Enthalpy-entropy compensation for the solubility of drugs in solvent mixtures: paracetamol, acetanilide, and nalidixic acid in dioxane-water, J. Pharm. Sci., 87, 1590 (1998). [ Links ]
31. M. Meloun, Z. Ferencíková, Enthalpy-entropy compensation for some drugs dissociation in aqueous solutions, Fluid Phase Equilib., 328, 31 (2012). [ Links ]
32. L.P. Pirila-Honkanen, P.A. Ruostesuo, Thermodynamic and spectroscopic properties of 2-pyrrolidinones. 1. Excess molar volumes of 2-pyrrolidinone + dichloromethane, + dimethyl sulfoxide, + acetone, + 2-propanol, and + water, J. Chem. Eng. Data, 32, 303 (1987). [ Links ]
33. G. Gonfa, M.A Bustam, N. Muhammad, S. Ullah, Density and excess molar volume of binary mixture of thiocyanate-based ionic liquids and methanol at temperatures 293.15-323.15 K, J. Mol. Liq., 211, 734 (2015). [ Links ]
34. Y. Marcus, "The properties of solvents", John Wiley & Sons, Inc., New York, 1998. [ Links ]
35. M.J. Kamlet, R.W. Taft, The solvatochromic comparison method. I. The betascale of solvent hydrogen-bond acceptor (HBA) basicities, J. Am. Chem. Soc., 98, 377 (1976). [ Links ]
How to cite this article
G.A.M. Areiza-Aldana, A. Cuellar-Lozano, N.A. Peña-Carmona, D.I. Caviedes-Rubio, A. Mehrdad, A.H. Miri, G.A. Rodríguez-Rodríguez, D.R. Delgado, Solution thermodynamics and preferential solvation of 3-chloro-N-phenyl-phthalimide in acetone + methanol mixtures, Rev. Colomb. Cienc. Quím. Farm., 45(2), 256-274 (2016).