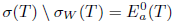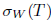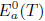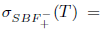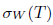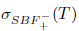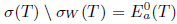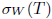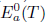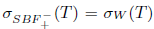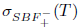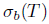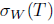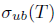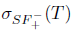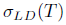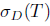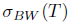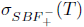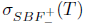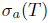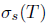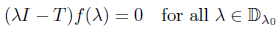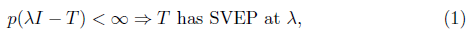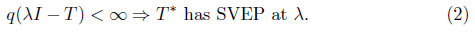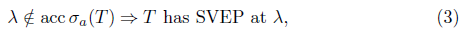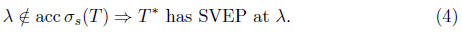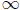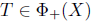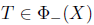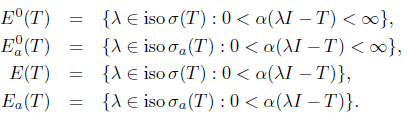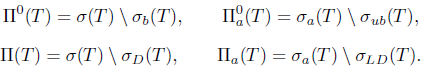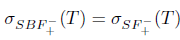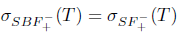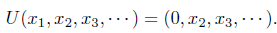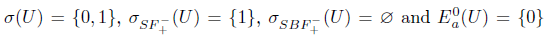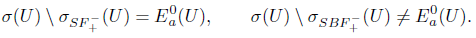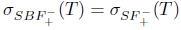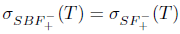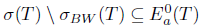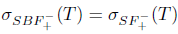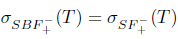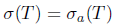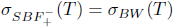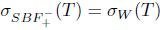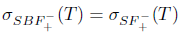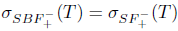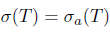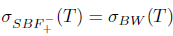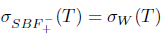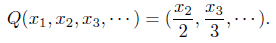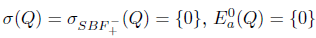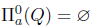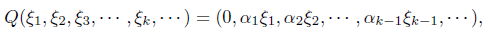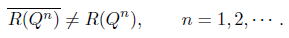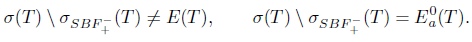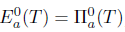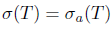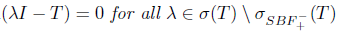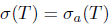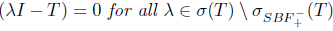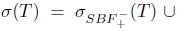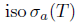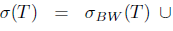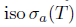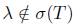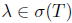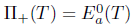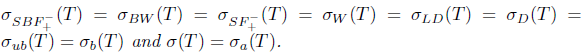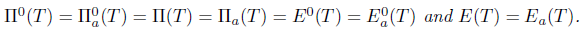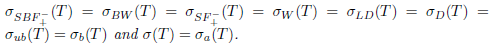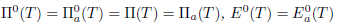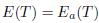1. Introduction and preliminaries
In this paper, we introduce two new spectral properties type Weyl-Browder theorems, namely the properties (Saw) and (Sab), respectively. In addition, we establish the precise relationships between these properties and others variants of Weyl's and Browder's theorem that have been recently introduced in [10,14,17,18,22,25] and [27].
Throughout this paper, L(X) denotes the algebra of all bounded linear operators acting on an infinite-dimensional complex Banach space X. We refer to [24] for details about notations and terminologies. However, we give the following notations that will be useful in the sequel:
Recall that an operator 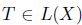 is said to have the single valued extension property at
is said to have the single valued extension property at 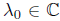 (abbreviated SVEP at λ0) if for every open disc
(abbreviated SVEP at λ0) if for every open disc 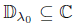 centered at λ0 the only analytic function
centered at λ0 the only analytic function 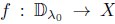 which satisfies the equation
which satisfies the equation
is 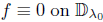 (see [16]). The operator T is said to have SVEP if it has SVEP at every point
(see [16]). The operator T is said to have SVEP if it has SVEP at every point 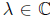 . Evidently, every
. Evidently, every 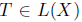 has SVEP at each point of the resolvent set
has SVEP at each point of the resolvent set 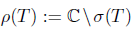 . Moreover, Τ has SVEP at every point of the boundary
. Moreover, Τ has SVEP at every point of the boundary 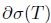 of the spectrum. In particular, Τ has SVEP at every isolated point of the spectrum. Note that (see [1, Theorem 3.8])
of the spectrum. In particular, Τ has SVEP at every isolated point of the spectrum. Note that (see [1, Theorem 3.8])
and dually
It is easily seen from definition of localized SVEP that
where acc K means the set of all accumulation points of  , and
, and
Remark 1.1. The implications (1)-(4) are actually equivalences whenever λΙ- Τ is a quasi-Fredholm operator, in particular when λΙ - Τ is semi B-Fredholm (see [2]).
Lemma 1.2. ([3, Lemma 2.4]) Let Τ G L(X). Then
The following lemma is a particular case of [9, Theorem 3.6].
Lemma 1.3. For Τ 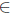 L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) λ0 Ι - Τ is left Drazin invertible ·
· λ0 Ι - Τ is quasi-Fredholm with finite ascent,
(ii) λ0 Ι - Τ is right Drazin invertible ·
· λ0 Ι - Τ is quasi-Fredholm with finite descent,
(iii) λ0 Ι-Τ is Drazin invertible ·
· λ0 Ι - Τ is quasi-Fredholm with finite ascent and descent.
Denote by iso K, the set of all isolated points of 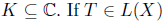 define
define
Also, define
Let 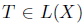 . Following Coburn [15], Τ is said to satisfy Weyl's theorem, in symbols (
. Following Coburn [15], Τ is said to satisfy Weyl's theorem, in symbols (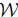 ), if
), if 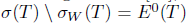 . Following Rakocevic ([20],[19]), Τ is said to satisfy
. Following Rakocevic ([20],[19]), Τ is said to satisfy 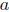 -Weyl's theorem, in symbols (
-Weyl's theorem, in symbols (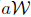 ), if
), if 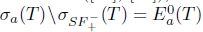 , and Τ is said to have property (w) if
, and Τ is said to have property (w) if 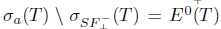 . According to Berkani and Koliha [11], Τ is said to satisfy generalized Weyl's theorem, in symbols
. According to Berkani and Koliha [11], Τ is said to satisfy generalized Weyl's theorem, in symbols 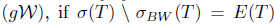 . Similarly, Τ is said to satisfy generalized a-Weyl's theorem, in symbol
. Similarly, Τ is said to satisfy generalized a-Weyl's theorem, in symbol 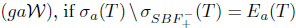 .
.
Now, we describe several spectral properties introduced recently in [7,10,13,14,17,18,22,23,25,26] and [27].
Definition 1.4. An operator Τ 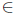 L(X) is said to have:
L(X) is said to have:
(i) property (gw) [7] if
.
(ii) property (b) [13] if
.
(iii) property (gb) [13] if
.
(iv) property (aw) [14] if
.
(v) property (gaw) [14] if
.
(vi) property (ab) [14] if 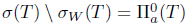 .
.
(vii) property (gab) [14] if
.
(viii) property (z) [25] if
.
(ix) property (gz) [25] if
.
(x) property (az) [25] if
.
(xi) property (gaz) [25] if
.
(xii) property (ah) [26] if
.
(xiii) property (gah) [26] if
.
(xiv) property (Bw) [17] if
.
(xv) property (Baw) [27] if
.
(xvi) property (Bgw) [22] if
.
(xvii) property (Bab) [27] if
.
(xviii) property (Bb) [22] if
.
(xix) property (Bgb) [22] if
.
(xx) property (SBaw) [10] if
.
(xxi) property (SBab) [10] if
.
(xxii) property (Sw) [23] if
.
(xxiii) property (Sb) [23] if
.
The properties (Bgw) and (Bgb) are also called (SBw) and (SBb), respectively (see [10]). Property ( Bb) was also introduced in [18].
2. Properties (Saw) and (Sab).
According to [24], Τ 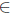 L(X) has property (gv) (resp. (v)) if
L(X) has property (gv) (resp. (v)) if 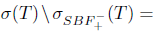
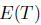 (resp.
(resp. 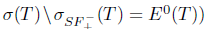 and it was proved in [24, Corollary 2.12], that property (gv) (resp. (v)) is equivalent to property (gz) (resp. (z)). Property (gv) (resp. (v)) also is called property (gt) (resp. (t)) in [21] and property (gh) (resp. (h)) in [26]. In this section we introduce and study two new spectral properties that are independent of property (gv) (and hence of property (gz)).
and it was proved in [24, Corollary 2.12], that property (gv) (resp. (v)) is equivalent to property (gz) (resp. (z)). Property (gv) (resp. (v)) also is called property (gt) (resp. (t)) in [21] and property (gh) (resp. (h)) in [26]. In this section we introduce and study two new spectral properties that are independent of property (gv) (and hence of property (gz)).
Definition 2.1. An operator Τ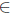 L(X) is said to have property (Saw) if
L(X) is said to have property (Saw) if 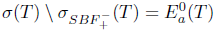 , and property (Sab) if
, and property (Sab) if 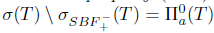 .
.
The next result gives the precise relationship between the properties (Saw) and (z).
Theorem 2.2. For Τ  L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) Τ has property (Saw),
Proof. (i)  (ii) Assume that Τ satisfies property (Saw) and let λ
(ii) Assume that Τ satisfies property (Saw) and let λ  σ(Τ) \
σ(Τ) \ 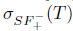 . Since
. Since 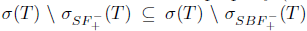 , we have λ
, we have λ 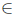 σ(Τ) \
σ(Τ) \ 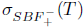 . As Τ satisfies property (Saw), it follows that λ
. As Τ satisfies property (Saw), it follows that λ 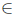
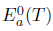 . This shows
. This shows 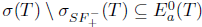 .
.
To show the opposite inclusion 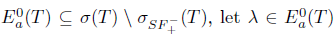 .
.
Then 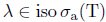 and
and 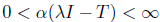 . Since Τ satisfies property (Saw), we have
. Since Τ satisfies property (Saw), we have 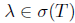 and λΙ - Τ is upper semi-B-Weyl. Thus, λΙ - Τ is an upper semi B-Fredholm operator and
and λΙ - Τ is upper semi-B-Weyl. Thus, λΙ - Τ is an upper semi B-Fredholm operator and 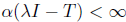 . By Lemma 1.2, we have that λΙ - Τ is an upper semi-Fredholm operator, so λΙ - Τ is an upper semi-Weyl operator. Hence,
. By Lemma 1.2, we have that λΙ - Τ is an upper semi-Fredholm operator, so λΙ - Τ is an upper semi-Weyl operator. Hence, 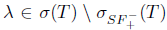 and so
and so 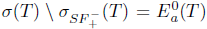 . This shows that Τ satisfies property (z). Consequently,
. This shows that Τ satisfies property (z). Consequently, 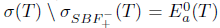 and
and 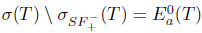 . Therefore,
. Therefore, 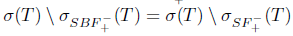
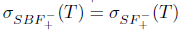 .
.
(ii) 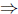 (i). Suppose that Τ satisfies property (z) and
(i). Suppose that Τ satisfies property (z) and 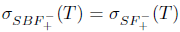 .
.
Then, 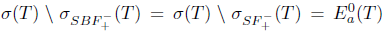 , and hence Τ satisfies property (Saw).
, and hence Τ satisfies property (Saw).
(ii) 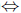 (iii). The equivalence between properties (z) and (v) has been proved in [24, Corollary 2.12].
(iii). The equivalence between properties (z) and (v) has been proved in [24, Corollary 2.12]. 
From Theorem 2.2, we observe that property (Saw) implies property (z). But the converse of this implication does not hold in general, as we can see in the following example.
Example 2.3. Let 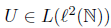 be defined by
be defined by
Hence, Τ satisfies property (z), but not property (Saw).
Similarly to Theorem 2.2, we have the following result.
Theorem 2.4. For Τ 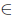 L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) Τ has property (Sab),
Proof. The proof (i) 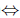 (ii), is similar to the proof (i)
(ii), is similar to the proof (i) 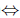 (ii) of Theorem 2.2. The proof (ii)
(ii) of Theorem 2.2. The proof (ii) 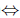 (iii), follows of the equivalence between properties (az) and (gaz) proved in [25, Corollary 3.5].
(iii), follows of the equivalence between properties (az) and (gaz) proved in [25, Corollary 3.5].
From Theorem 2.4, we note that property (Sab) implies property (az). But the converse is not true in general as shown by the following example.
Example 2.5. Consider the operator T = 0 defined on the Hilbert space 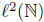 .
.
Then, 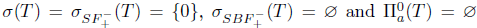 . Therefore,
. Therefore, 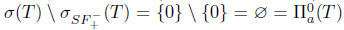 and
and 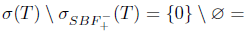
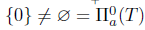 . Thus, T satisfies property (az), but not property (Sab).
. Thus, T satisfies property (az), but not property (Sab).
The next result gives the relationship between the properties (Saw) and (SB aw).
Theorem 2.6. Let T 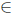 L(X). Then T has property (Saw) if and only if T has property (SBaw) and
L(X). Then T has property (Saw) if and only if T has property (SBaw) and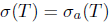 .
.
Proof. Sufficiency: Assume that T satisfies property (Saw) and 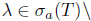
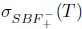 . Since
. Since 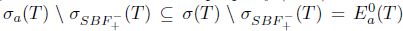 , we have
, we have 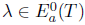 and so,
and so, 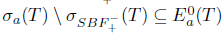 .
.
To show the opposite inclusion 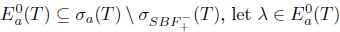 . Then,
. Then, 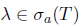 and since T satisfies property (Saw), it follows that
and since T satisfies property (Saw), it follows that 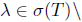
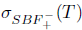 and so,
and so, 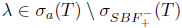 . Hence,
. Hence, 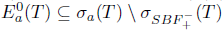 and T satisfies property (SBaw). Consequently,
and T satisfies property (SBaw). Consequently, 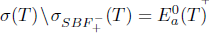 and
and 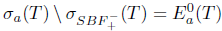 . Therefore,
. Therefore, 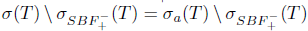 and
and 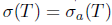 .
.
Necessity: Assume that T satisfies property (SBaw) and 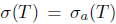 . Then,
. Then, 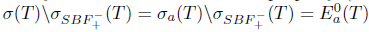 . Thus,
. Thus, 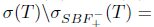
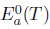 and T satisfies property (Saw).
and T satisfies property (Saw). 
Similarly to Theorem 2.6, we have the following result.
Theorem 2.7. Let T 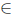 L(X). Then T has property (Sab) if and only if T has property (SBab) and
L(X). Then T has property (Sab) if and only if T has property (SBab) and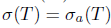 .
.
Proof. The proof is similar to the proof of Theorem 2.6. 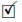
The next example shows that, in general, property (SBaw) (resp. (SBab)) does not imply property ( Saw) (resp. ( Sab)).
Example 2.8. Let R be the unilateral right shift operator on 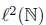 and U be the operator defined in Example 2.3. Define an operator T on
and U be the operator defined in Example 2.3. Define an operator T on 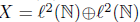 by
by 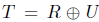 . Then,
. Then, 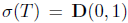 , the closed unit disc on
, the closed unit disc on 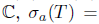
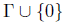 , where Γ denotes the unit circle of
, where Γ denotes the unit circle of 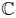 and
and 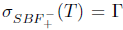 . Moreover,
. Moreover, 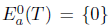 and
and 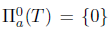 . Therefore,
. Therefore, 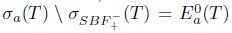
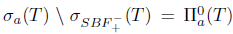 . Thus, T satisfies both properties (SBaw) and (SBab). On the other hand,
. Thus, T satisfies both properties (SBaw) and (SBab). On the other hand, 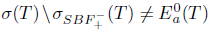 and
and 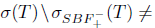
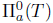 . Therefore, T does not satisfy property (Saw) or property (Sab).
. Therefore, T does not satisfy property (Saw) or property (Sab).
Corollary 2.9. Let T 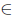 L(X). Then:
L(X). Then:
(i) T has property ( Saw) if and only if T has property (Sw).
(ii) T has property ( Sab) if and only if T has property (Sb).
Proof.
(i) Suppose that T satisfies property (Saw). By Theorem 2.6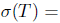
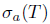 and so,
and so, 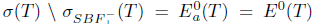 . Therefore, T satisfies property ( Sw).
. Therefore, T satisfies property ( Sw).
Conversely, assume that T satisfies property (Sw). By [23, Theorem 2.25], 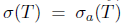 and so,
and so, 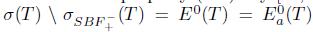 . Therefore, T satisfies property (Saw).
. Therefore, T satisfies property (Saw).
(ii) The proof is similar to the proof of (i). Just use both Theorem 2.7 and [23, Theorem 2.28].

The next result gives the relationship between the properties (Saw) and ( Baw).
Theorem 2.10. Let T 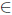 L(X). Then T has property (Saw) if and only if T has property (Baw) and
L(X). Then T has property (Saw) if and only if T has property (Baw) and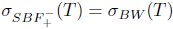 .
.
Proof. Sufficiency: Suppose that T satisfies property (Saw), that is 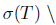
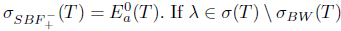 , then λI - T is a B-Weyl operator, and hence it is upper semi-B-Weyl. Thus
, then λI - T is a B-Weyl operator, and hence it is upper semi-B-Weyl. Thus 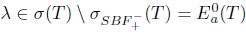 , and
, and
To show the opposite inclusion 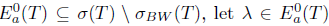 . Since T satisfies property (Saw), λ
. Since T satisfies property (Saw), λ 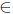 iso
iso 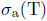 and λI - T is an upper semi-B-Predholm operator, hence quasi-Predholm. By Theorem 2.6, λ
and λI - T is an upper semi-B-Predholm operator, hence quasi-Predholm. By Theorem 2.6, λ 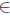 iso
iso 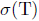 , it follows that both T and T* have SVEP in λ, and by Remark 1.1, 0 <
, it follows that both T and T* have SVEP in λ, and by Remark 1.1, 0 < 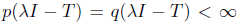 . Prom Lemma 1.3, we have λI - T is a Drazin invertible operator, and hence it is B-Weyl. Therefore,
. Prom Lemma 1.3, we have λI - T is a Drazin invertible operator, and hence it is B-Weyl. Therefore, 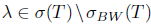 , and so
, and so 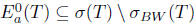 . This shows that T satisfies property (Baw). Consequently,
. This shows that T satisfies property (Baw). Consequently, 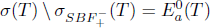 and
and 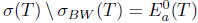 . Therefore,
. Therefore, 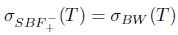 .
.
Necessity: Suppose that T satisfies property (Baw) and 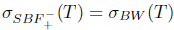 . Then,
. Then, 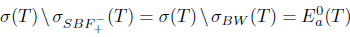 , and so T satisfies property (Saw).
, and so T satisfies property (Saw). 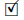
Similarly to Theorem 2.10, we have the following result.
Theorem 2.11. Let T  L(X). Then T has property (Sab) if and only if T has property (Bab) and
L(X). Then T has property (Sab) if and only if T has property (Bab) and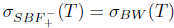 .
.
Proof. The proof is similar to the proof of Theorem 2.10. 
The next example shows that, in general, property (Baw) (resp. (Bab)) does not imply property (Saw) (resp. (Sab)).
Example 2.12. Let R be the unilateral right shift operator on 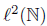 . Define an operator T on
. Define an operator T on 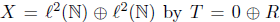 . Then,
. Then, 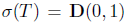 ,
, 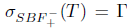 . Moreover,
. Moreover, 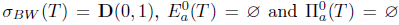 .
.
Therefore, 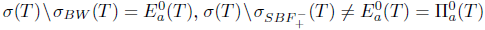 . Thus, T satisfies property (Baw) and hence property (Bab), but not property (Saw) or property ( Sab).
. Thus, T satisfies property (Baw) and hence property (Bab), but not property (Saw) or property ( Sab).
The next result gives the relationship between the properties (Saw) and (aw).
Theorem 2.13. Let T 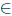 L(X). Then T has property (Saw) if and only if T has property (aw) and
L(X). Then T has property (Saw) if and only if T has property (aw) and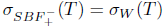 .
.
Proof. Sufficiency: Assume that T satisfies property (Saw); then it also satisfies property (Baw) by Theorem 2.10. Property (Baw) implies by [27, Theorem 3.3] that T satisfies property (aw). Consequently, 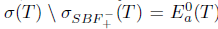 and
and 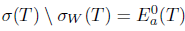 . Therefore,
. Therefore, 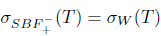 .
.
Necessity: Suppose that T satisfies property (aw) and 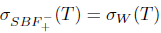 . Then,
. Then, 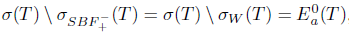 , and hence T satisfies property ( Saw).
, and hence T satisfies property ( Saw). 
Similarly to Theorem 2.13, we have the following result.
Theorem 2.14. Let T  L(X). Then T has property (Sab) if and only if T has property (ab) and
L(X). Then T has property (Sab) if and only if T has property (ab) and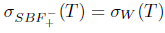 .
.
Proof. The proof is similar to the proof of Theorem 2.13. Just use both Theorem 2.11 and [27, Theorem 3.6]. 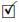
The next example shows that, in general, property ( aw) (resp. (ab)) does not imply property (Saw) (resp. ( Sab)).
Example 2.15. Let R be the unilateral right shift operator on 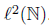 . Then,
. Then, 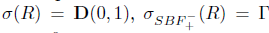 . Moreover,
. Moreover, 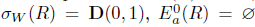
and 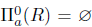 . Therefore,
. Therefore, 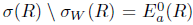 and
and 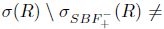
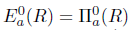 . Thus, R satisfies property (aw) and hence property (ab), but not property (Saw) or property (Sab).
. Thus, R satisfies property (aw) and hence property (ab), but not property (Saw) or property (Sab).
As a consequences of the results above, we have the following two corollaries, where we give new characterizations of the properties (Sw) and (Sb), respectively.
Corollary 2.16. For T 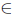 L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) T has property (Sw),
Corollary 2.17. For T 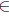 L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) T has property (Sb),
Recall that T 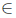 L(X) is said to satisfy a-Browder's theorem (resp. generalized
L(X) is said to satisfy a-Browder's theorem (resp. generalized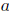 -Browder's theorem) if
-Browder's theorem) if  (resp.
(resp. 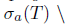
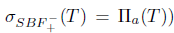 . From [8, Theorem 2.2] (see also [4, Theorem 3.2(ii)]),
. From [8, Theorem 2.2] (see also [4, Theorem 3.2(ii)]), 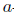 -Browder's theorem and generalized a-Browder's theorem are equivalent. It is well known that a-Browder's theorem for T implies Browder's theorem for T,
-Browder's theorem and generalized a-Browder's theorem are equivalent. It is well known that a-Browder's theorem for T implies Browder's theorem for T, 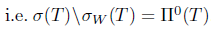 . Also by [8, Theorem 2.1], Browder's theorem for T is equivalent to generalized Browder's theorem for
. Also by [8, Theorem 2.1], Browder's theorem for T is equivalent to generalized Browder's theorem for 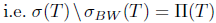 .
.
The next result gives the relationship between the properties (Saw) and (Sab).
Theorem 2.18. Let T 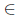 L(X). Then T has property (Saw) if and only if T has property (Sab) and
L(X). Then T has property (Saw) if and only if T has property (Sab) and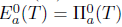 .
.
Proof. Sufficiency: Assume that T satisfies property (Saw); then it satisfies property (SBaw), by Theorem 2.6. Property (SBaw) implies by [10, Theorem 2.12] that T satisfies a-Weyl's theorem, o equivalently T satisfies a-Browder's theorem and 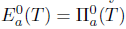 [5, Theorem 2.14]. Since that T satisfies property (Saw), it follows that
[5, Theorem 2.14]. Since that T satisfies property (Saw), it follows that 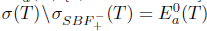 , and hence
, and hence 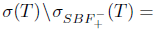
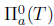 .
.
Necessity: Suppose that T satisfies property (Sab) and 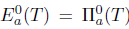 . Then
. Then 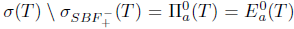 and so T satisfies property (Saw).
and so T satisfies property (Saw). 
The next example shows that property (Sab) does not imply property (Saw).
Example 2.19. Consider 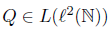 defined as
defined as
Hence, T satisfies property (Sab), but not property (Saw).
Corollary 2.20. For T 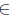 L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) T has property (Saw),
(ii) T has properties (Sab) and (SBaw).
(iii) T has property (Sab) and satisfies a-Weyl's theorem.
Proof.
Follows immediately from the proof of Theorem 2.18. 
The following two examples show that the properties (Saw) (resp. (Sab)) and (gv) (or (gz)) are independient.
Example 2.21. Consider the operator T defined in Example 2.5. Then, 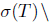
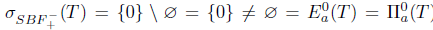 , and hence T does not satisfy property (Saw) or property (Sab). Moreover, we have
, and hence T does not satisfy property (Saw) or property (Sab). Moreover, we have 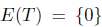 . Consequently,
. Consequently, 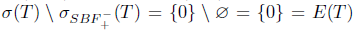 and so, T satisfies property (gv).
and so, T satisfies property (gv).
Example 2.22. Let Q be defined for each 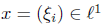 by
by
where (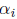 ) is a sequence of complex numbers such that
) is a sequence of complex numbers such that 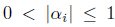 and
and 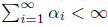 . It follows from [11, Example 3.12], that
. It follows from [11, Example 3.12], that
Define the operator T on 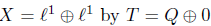 . Then,
. Then, 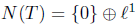
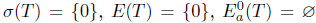 . Since
. Since 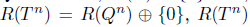 is not closed for any n
is not closed for any n 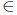 N; so T is not an upper semi B-Weyl operator and -
N; so T is not an upper semi B-Weyl operator and - 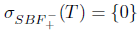 . We then have,
. We then have,
Hence, T satisfies property (Saw) and hence property (Sab), but does not satisfy property ( gv).
In the next theorem we give a new characterization of operators having property ( Sb).
Theorem 2.23. Let T 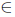 L(X). Then T has property (Sb) if and only if T has (Bb) and ind
L(X). Then T has property (Sb) if and only if T has (Bb) and ind 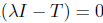 for all
for all 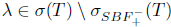 .
.
Proof. Sufficiency: Assume that T satisfies property (Sb); then it also satisfies property (Bb), by [23, Theorem 2.6]. Let 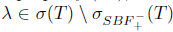 , as T satisfies property (Sb), then
, as T satisfies property (Sb), then 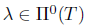 . Thus
. Thus 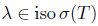 and
and 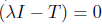 .
.
Necessity: Suppose that T satisfies property (Bb) and ind 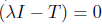 for all
for all 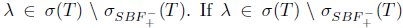 , then
, then 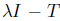 is an upper semi-B-Fredholm operator with ind
is an upper semi-B-Fredholm operator with ind 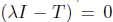 , it follows that
, it follows that 
 , and as T satisfied property
, and as T satisfied property 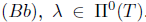 . This shows
. This shows 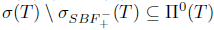 . Conversely, let
. Conversely, let 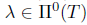 . Then
. Then 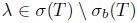 and hence
and hence 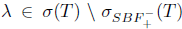 . Thus,
. Thus, 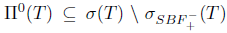 and T satisfies property (Sb).
and T satisfies property (Sb). 
Corollary 2.24. For T  L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) T has property (Saw),
Proof. The equivalence (i)  (ii) follows immediately from Theorem 2.18 and Corollary 2.9. The equivalence (i)
(ii) follows immediately from Theorem 2.18 and Corollary 2.9. The equivalence (i)  (iii) follows immediately from Corollary 2.9 and [23, Theorem 2.25]. The equivalence (i)
(iii) follows immediately from Corollary 2.9 and [23, Theorem 2.25]. The equivalence (i)  (iv) follows immediately from Corollary 2.9 and [23, Theorem 2.8].
(iv) follows immediately from Corollary 2.9 and [23, Theorem 2.8]. 
Similarly to Corollary 2.24, we have the following result.
Corollary 2.25. For T  L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) T has property ( Sab),
Proof. The equivalence (i)  (ii) follows immediately from Corollary 2.9 and [23, Theorem 2.8]. The equivalence (i)
(ii) follows immediately from Corollary 2.9 and [23, Theorem 2.8]. The equivalence (i)  (iii) follows immediately from Corollary 2.9 and Theorem 2.23.
(iii) follows immediately from Corollary 2.9 and Theorem 2.23. 
Theorem 2.26. Suppose that T G L(X) has property (Saw). Then:
Proof. (i) By [6, Theorem 2.4], it is sufficient to prove that T has SVEP at every 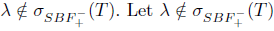 . We have the following two cases.
. We have the following two cases.
In Case 1, clearly T has SVEP at λ. In Case 2, we have 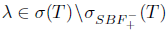 and since T satisfies property (Saw), it follows that
and since T satisfies property (Saw), it follows that 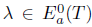 . Therefore,
. Therefore, 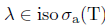 and so T has SVEP at λ again.
and so T has SVEP at λ again.
To show the equality 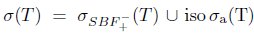 , observe first that
, observe first that 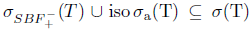 holds for every T
holds for every T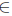 L(X). To show the opposite inclusion, suppose that
L(X). To show the opposite inclusion, suppose that 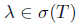 and
and 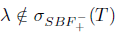 . Then
. Then 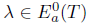 , since T satisfies property (Saw). Therefore,
, since T satisfies property (Saw). Therefore, 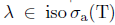 , and so
, and so 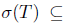
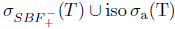 . This shows that
. This shows that 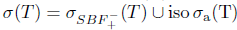 .
.
(ii) Follows from (i), by using the fact that generalized a-Browder's theorem implies generalized Browder's theorem, and the equality
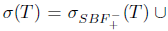
, implies the inclusion
, leading to
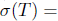
.
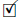
For T 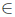 L(X), define
L(X), define 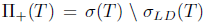 . The precise relationship between generalized a-Browder's theorem and property (Saw) is described by the following theorem.
. The precise relationship between generalized a-Browder's theorem and property (Saw) is described by the following theorem.
Theorem 2.27. For T 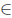 L(X), the following statements are equivalent:
L(X), the following statements are equivalent:
(i) T has property (Saw),
Proof. (i) 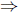 (ii) Assume that T satisfies property (Saw). Then, by Theorem 2.26, it is sufficient to prove
(ii) Assume that T satisfies property (Saw). Then, by Theorem 2.26, it is sufficient to prove 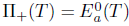 . Indeed,
. Indeed, 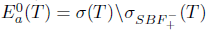
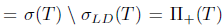 , since T satisfies property (Saw) and generalized
, since T satisfies property (Saw) and generalized 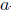 -Browder's theorem by Theorem 2.27.
-Browder's theorem by Theorem 2.27.
(ii)  (i) If T satisfies generalized
(i) If T satisfies generalized 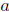 -Browder's theorem and
-Browder's theorem and 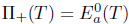 , then
, then 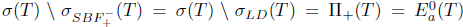 . Therefore, T satisfies property (Saw).
. Therefore, T satisfies property (Saw). 
Corollary 2.28. If T  L(X) has SVEP at each
L(X) has SVEP at each , then T has property (Saw) if and only if
, then T has property (Saw) if and only if 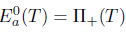 .
.
Proof. The hypothesis T has SVEP at each 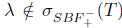 , implies that T satisfies generalized a-Browder's theorem. Therefore, if
, implies that T satisfies generalized a-Browder's theorem. Therefore, if 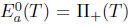 , then
, then 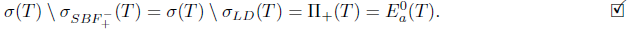
Remark 2.29. It was proved in [12, Lemma 2.4], that if T* has SVEP at every 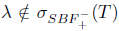 (resp. T has SVEP at every
(resp. T has SVEP at every 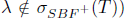 , then
, then 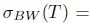
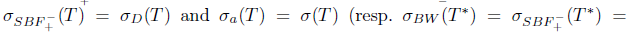
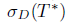 and
and 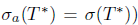 . Under the above results, clearly we have that if T* has SVEP at every
. Under the above results, clearly we have that if T* has SVEP at every 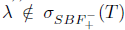 (resp. T has SVEP at every
(resp. T has SVEP at every 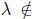
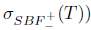 , then the properties (Bw), (Sw), (Saw), (Bgw), (Baw) and (SBaw) are equivalent for T (resp. for T* ). In the same form, we obtain equivalence for the properties (Bb), (Sb), (Sab), ( Bgb), (Bab) and (SBab).
, then the properties (Bw), (Sw), (Saw), (Bgw), (Baw) and (SBaw) are equivalent for T (resp. for T* ). In the same form, we obtain equivalence for the properties (Bb), (Sb), (Sab), ( Bgb), (Bab) and (SBab).
Theorem 2.30. Suppose that T 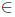 L(X) has property property (Saw). Then:
L(X) has property property (Saw). Then:
(iii) The properties (SBaw), (SBab), (Bgw), (Bgb), (w), (b), (gb), (z), (az), (gaz), (v), (ah), (gah), (Baw), (Bab), (gab), (Bw), (Bb), (aw), (ab), (
), (a
), (g
), (ga
), (
) and (a
) for T are equivalent, and T satisfies each ofthese properties.
(iv) The properties (gw), (gz), (gv), (gaw), (g
) and (ga
) for T are equivalent.
Proof. (i) By Theorem 2.6, the equality σ(Τ) = σα(Τ) holds. The equalities 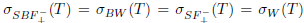 follows from Theorems 2.2, 2.10 and 2.13. Since the inclusions
follows from Theorems 2.2, 2.10 and 2.13. Since the inclusions 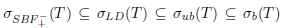 and
and 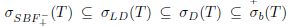 hold, it is sufficient to prove
hold, it is sufficient to prove 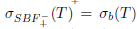 . Indeed,
. Indeed, 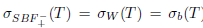 , since Τ satisfies property (Saw) and generalized Browder's theorem or equivalently Browder's theorem, by Theorem 2.27.
, since Τ satisfies property (Saw) and generalized Browder's theorem or equivalently Browder's theorem, by Theorem 2.27.
(ii) The equalities 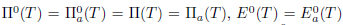 and
and 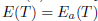 follows from (i). By Theorem 2.18, the equality
follows from (i). By Theorem 2.18, the equality 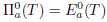 holds.
holds.
(iii) By Theorem 2.2, Τ satisfies property (z), and the equivalence between all properties follows from (i) and (ii).
(iv) Follows from (i) and (ii). 
Similarly to Theorem 2.30, we have the following result.
Theorem 2.31. Suppose that Τ  L(X) has property (Sab). Then:
L(X) has property (Sab). Then:
(iii) The properties (SBab), (Bgb), (b), (gb), (az), (gaz), (ah), (gah), (Bab), (gab), (Bb), (ab), (
), (
), (
) and (
) for Τ are equivalent, and Τ satisfies each of these properties.
(iv) The properties (SB
w), (Bgw), (w), (z), (v), (B
w), (Bw), (
w), (
) and (
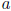
) for Τ are equivalent.
(v) The properties (gw), (gz), (gv), (gaw), (gW) and (g
) for Τ are equivalent.
In the following diagram arrows mean implications between the properties defined above. The numbers near the arrows are references to the results in the present paper (numbers without brackets) or to the bibliography therein (numbers in square brackets).