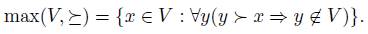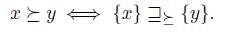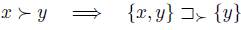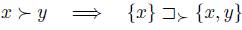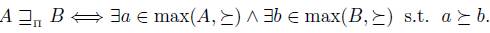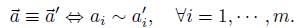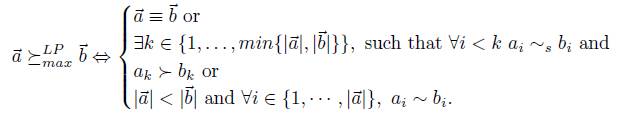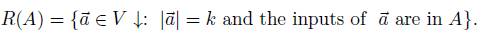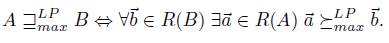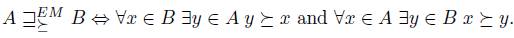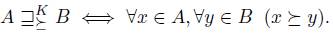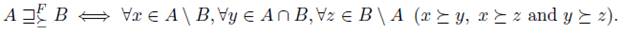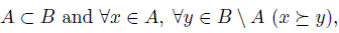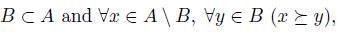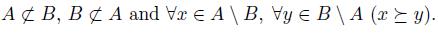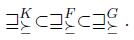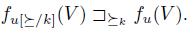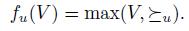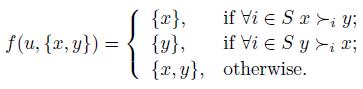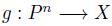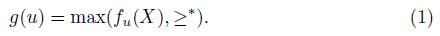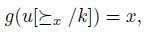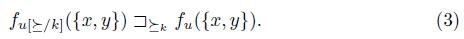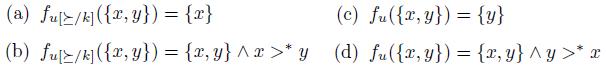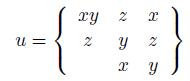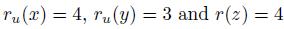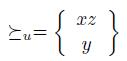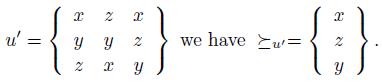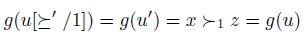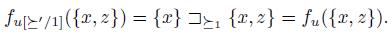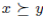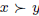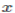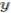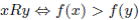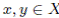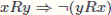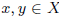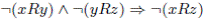English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
Studying preferences is now a common issue in different domains: (qualitative) Decision Making under Uncertainty [18,17], Merging Information in Logical Frameworks [34,35,36], Knowledge Representation [13], Belief Dynamics [1], Social Choice [2,41], etc. Via this common issue, preferences, there are some interesting problems which can be translated from one domain to another [35,25]. That is the case of some works on Information Fusion and Belief Merging [23,12]. In these works the concept of strategy-proofness, coming from Social Choice Theory, is studied. However, the results of these works are not, in our view, general enough. Actually, the question of finding general results of manipulability in the framework of Belief merging remains open. On the contrary, the problem of manipulation in the framework of Social Choice Theory has been studied extensively and successfully. However, we think that there are still some things to say about manipulation in this setting, in particular there are notions of manipulation which are very natural and easily translated to the setting of Belief Merging. The current work concerns the first part of our project: the presentation of very natural and simple results of manipulation in the framework of Social Choice Theory. The second part, the utilization of these results in the framework of Belief Merging is an ongoing work.
With the aim of offering a means for a better understanding of the problem of manipulability, we give below some intuitive explanations of the concepts involved in this work.
Let us begin by explaining very roughly what Social Choice is. When we face the problem of selecting the best candidates of a list, related to some individual preferences over the candidates, we are actually facing a problem of Social Choice. More precisely, the general issue addressed by Social Choice Theory is the study of such procedures of selection.
The first important question asked in this domain is what a good selection procedure is (they are called social choice functions) and, of course, if such functions exist. The main idea, in order to establish what a good social choice function is, consists in defining a set of rational properties that a good function has to satisfy. A very small set of these properties that seem very sensible (absence of dictatorship, Pareto dominance, transitive explanations, independence of irrelevant alternatives and the totality of the procedure -see Section 2 for a precise formulation-) appears as the minimum set of conditions that a good function has to satisfy. As a matter of fact, they are incompatible. Precisely, the surprising1 result of Arrow [2,32,46], known as Arrow's Impossibility Theorem, says that there are no such functions (in Section 2 we find the precise formulation).
Another important question can be formulated in the following terms. Which are the properties of social choice functions that guarantee they are free of manipulation? This is the issue addressed in the current work. Since the precise and partial formulation of this problem by Gibbard and Satterthwaite in 1973 [28,43] and their interesting solution, many works have been done in this domain. A good survey in which we can find the most important works on manipulation is [46]. The Gibbard-Satterthwaite's Theorem states that a large class of social choice functions are manipulable. The class of functions where the result applies is given by the functions mapping a set of individual preferences into an alternative (and having a range of cardinal bigger or equal to three, i.e. having al least three outputs). Note that for this kind of functions it is quite natural and easy to define manipulability: a function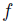 
is manipulable if there exists an input u (thought of as the vector of the true preferences2 of individuals), there exists an individual i such that his true preference is 
and another preference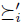 
such that if u' is the input resulting of replacing in u, the preference 
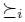by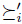 
, we have 
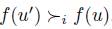. This can be interpreted as follows: in situation u, it is more convenient for individual i (the manipulator) to lie, i.e. giving 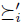as its preferences, rather than to give his true preferences! Doing that, the result obtained, 
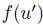, is strictly preferred by him over 
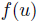. Remark that when the output of 
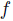is a set of candidates, a natural way to define manipulation is to consider extensions of the relations 
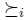to sets of candidates. We call these extensions liftings (see Section 3). This is the point of view to be developed in this work.
As we already said, many works have followed the pioneering results of Gibbard and Satterthwaite. Among them, we have to mention the works of Duggan and Schwartz [21], Barberà et al. [6], Benoit [7] where they give very general manipulability theorems for some classes of social choice functions. The classes concern functions giving sometimes ties as a result. They consider restricted domains and the functions they consider are in fact social choice correspondences (functions mapping profiles into preferences) which are not exactly social choice functions (see Section 2). We cite these works because the preferences in the profiles considered are total preorders which are more general than linear orders and actually of the same type of profiles we considered. However, our work is more related to the Barberà-Kelly Theorem [3,31] (see Section 4 for more details). Actually, we give an interesting weak version of this Theorem. One of the contributions of this work is to give a direct proof of it which introduces a new technique based on the notion of lifting preferences, and uses the original Gibbard-Satterthwaite Theorem. One of the accomplishments of our manipulability Theorem (Theorem 4.5) is to capture a very large number of ways in which a social choice function can be manipulated. Particularly, we isolate two simple conditions on the liftings that entail manipulability.
We have to say that some particular ways of making lifting of preferences have been considered in the literature concerning the manipulability problem. The first work, in that sense, is perhaps the one of Gardenfors [26]. However, Fishburn [24] considers a particular lifting in establishing some general results of impossibility. More recently, Brandt [10] considers manipulability with respect to the lifting of Kelly and establishes, among other interesting results, that the social choice functions which are Condorcet extensions are always manipulable. Also, Brandt and Brill [11] consider the Gardenfors and Fishburn liftings. They establish necessary and sufficient conditions for manipulability of non resolute rules where the notions of preference over sets of alternatives involved in manipulability are given by the lifting of Gardenfors and the lifting of Fishburn.
We organize the rest of this work as follows. Section 2 contains the basic concepts and classical results we need in the subsequent Sections. Section 3 presents our main tool, the concept of lifting. Therein we establish some properties of it and some natural examples. In Section 4, we give the concept of manipulability related to a lifting and examine the manipulability with respect to some classes of liftings. We state the Barberà-Kelly's Theorem and we see how to obtain our manipulability result as a consequence of this Theorem. We give also a direct, natural and informative proof of our result. Section 5 is devoted to comparing our work with other related results. Finally, we end with Section 6, containing some remarks about our results.
2. Preliminaries
We suppose we have a nonempty and finite set N of individuals. Let n be the cardinality3 of N, actually we suppose N = {1,..., n}. Let X be a nonempty finite set. X will be called the set of alternatives. An (individual) preference will be a total pre-order over X, i.e. a transitive and total relation. Note that reflexivity of 
follows of totality. A partial preference is a transitive and reflexive relation that is not necessarily a total relation.
The relation of strict preference associated to a preference is denoted 
and is defined by 
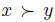iff 
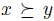and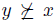 
. When 
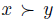we read 
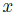is preferred to 
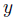. Note that, if 
is a total pre-order, the relation 
associated to it, is a weak order (or equivalently a modular relation4), i.e. an asymmetric and negatively transitive relation5.
The set of total pre-orders over X will be denoted P. An element u of P
n (the cartesian product of P, n times) is called a profile. In the profile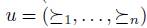 
, the preference 
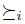denotes the preference of the individual i. A nonempty subset of X is called an agenda. The set of agendas will be denoted 
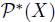, i.e. the set of nonempty subsets of X.
If V is an agenda and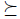 
is a total pre-order over X, we define the set of maximal elements of V with respect to 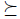, denoted max(
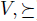) as follows:
Definition 2.1. A social choice function is a function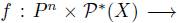 
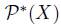such that 
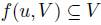. Often 
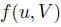will be denoted 
.
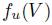Most approaches in Social Choice Theory (see for instance [32]) present a "curryfied" vision of what we call a social choice function. First they consider a function from profiles into functions mapping agendas into agendas. These functions are called social choice rules and the functions C mapping agendas into agendas with the property that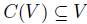 
are called choice functions.
Now we define some rational desirable properties for social choice functions. The fact that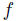 
is total, |N| ≥ 3 and |X | ≥ 3 is known as the Standard Domain Condition. Totality guarantees an outcome for any profile (this relates to the notion of impartial culture in social choice).
Let V be a nonempty subset of X. Let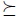 
a preference. We denote by 
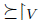the restriction to V of the relation 
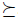. If 
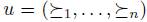then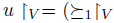 
. 
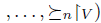A social choice function f satisfies the Independence of Irrelevant Alternatives Property if and only if for all 
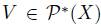and for all 
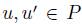if 
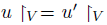then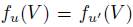 
. This condition states that the result of selecting on an agenda V depends only on the individual preferences on V.
We say that a social choice function f satisfies the Strong Pareto Condition if for all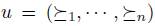 
and V the following condition holds: if for any 
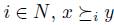, there exists 
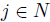such that 
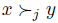and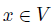 
, then 
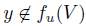. In particular, if 
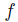satisfies the Standard Domain Condition and 
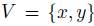, the Strong Pareto Condition says that if for all the individuals, x is not less preferred than y and if for at least one individual x is preferred to y, then selecting the best elements of V, will give only x.
A social choice function f satisfies Transitive Explanations if for every profile u there exists a total pre-order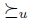 
such that 
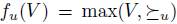, for any agenda V. This is a very interesting property. It says that there is a very uniform way for choosing the best elements of agendas when the profile is fixed. In other words, in the economists view, the social choice rule (the first step in the process) consists in giving an aggregation total pre-order 
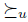to the input u and then the choice function (the second step) consists in taking the maximal elements (the preferred ones) of the agenda V with respect to this relation 
.
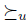All four previous properties seem to be very good and rational properties for a social choice function. A last property which is desirable for a social choice function is the absence of a dictator, where a dictator is defined in the following way: the individual i is a dictator for f if for all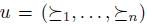 
in Pn, for all 
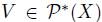, and for all 
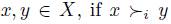and 
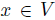then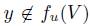 
. It is interesting to note that if there is a dictator i, and if in the profile u the preference 
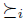is a linear order6 then 
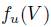is the preferred element (the maximal) of V with respect to 
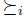. Another interesting remark is that, in presence of Transitive Explanations, the preference aggregation relation 
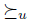coincides with the preference relation of the dictator, whenever the dictator preference is a linear order.
Now, having stated the previous properties, we can formulate the notable Arrow's result [2]. It tells us that it is impossible to have a function for which these five good properties hold (for a proof we can also see [32] or [38]; in the last reference one can find a very interesting analysis of the proof). More precisely, it can be stated as follows.
Theorem 2.2.
If a social choice function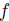
satisfies the Standard Domain Condition, the Independence of Irrelevant Alternatives Property, the Strong Pareto Condition and Transitive Explanations, then f has a dictator.
Based on Arrow's Theorem, Gibbard [28] and Satterthwaite [43] independently give a proof of what is today known as the Gibbard-Satterthwaite's Theorem. In order to state this result, we need the following concepts.
Definition 2.3. A function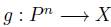 
will be called a Voting scheme.
If a Voting scheme g is onto7, |X| ≥ 3 and n ≥ 3, we will say that g satisfies the Gibbard Standard Domain Condition.
If u is a profile and 
is a preference, we denote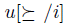 
the profile that coincides with u for the individuals 
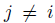and for i is 
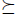, that is to say if 
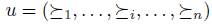, then 
.
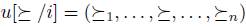The individual i is called a Gibbard Dictator for g if for all x there exists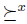 
such that for every profile 
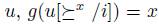. That is to say, if individual i wants x to be the winner, he can attain it by choosing well his preferences independently of the other individual preferences.
Definition 2.4. A voting scheme g is said to be ,manipulable iff there exist k,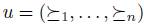 
and 
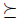such that 
.
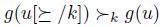Note that this definition formalizes the concept of manipulation for voting schemes described in the Introduction. In other words, it says that the individual k (the manipulator) obtains a strictly better result with respect to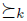 
(his true preference) if he lies, that is, if he changes his preference to 
.
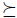When a voting scheme g is manipulable and a triple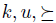 
is a witness of the manipulability of g as in the previous definition, we say that such a triple is a situation of manipulation.
Theorem 2.5. Any voting scheme g satisfying the Gibbard Standard Domain Condition is manipulable or has a Gibbard Dictator.
For a proof of this result one can see, of course, the sources [28,43]. We can also find interesting proofs in [42,46].
It is quite clear that a social choice function (Definition 2.1) and a voting scheme (Definition 2.3) are very different. Actually, one could see a voting scheme g as generated by a very particular social choice function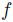 
, by the following statement: 
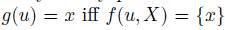. Of course, the class of social choice functions generating voting schemes via the previous statement is very restricted because this imposes the absence of ties when the agenda is the whole X.
Thus, a generalization of Theorem 2.5 to social choice functions is not so straightforward. Then, the first thing to do is to give a definition of manipulability for social choice functions, i.e. to find the definition corresponding to Definition 2.3, in the setting of social choice functions. Interesting works have been done in the past years in this direction. In Section 5, we will show some connections of those works with our work. In particular, we show some similarities and some differences.
One way to perform this, is considering only the functions satisfying Transitive Explanations and seeing the social choice function as a function taking values in P, i.e. the outputs are preferences. This can be done because the social choice functions having Transitive Explanations satisfy the following proposition.
Proposition 2.6. Suppose that the social choice function f satisfies Transitive Explanations and Standard Domain Condition. For each profile u, define a total pre-order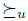 
as follows:
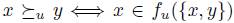. Then 
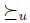is the unique total pre-order that satisfies
.
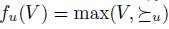By the previous result, it is easy to see a function having Transitive Explanations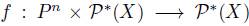 
as a function 
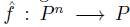. The function 
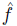is defined by 
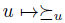where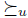 
is the unique total pre-order satisfying 
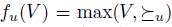. Conversely, having 
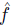, mapping 
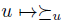, we define 
by putting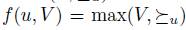 
. By abuse of notation, we identify 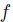and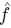 
. With this identification in mind, we want to find out what a manipulation situation is. The obvious choice is to take a triple 
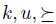such that 
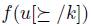is strictly better than 
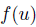. But the problem is that we need relations between preferences in order to give full sense to the previous phrase. Actually, we would need a preference 
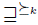over preferences such that 
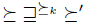expresses that the preference 
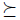is better, relative to 
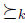, than 
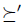. Although this kind of approach seems interesting and promising, it is not used in this work because of the difficulty to define a rational relation 
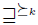in such a way that it has a clear intuitive meaning8. Actually, using this approach, it is hard to see in which way the output of 
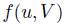(a set of alternatives) is better than 
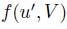(another set of alternatives).
The approach used to tackle the problem of manipulability in this work is to take into account all the inputs of a social choice function. In particular, a situation of manipulability will be a quadrupl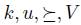e 
where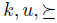 
are as before and V is an agenda such that 
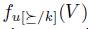is better than 
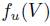, relative to the lifting of 
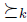. To define liftings in a precise manner and to study some of their properties is the goal of the following Section.
3. Lifting preferences
Transferring the information from preferences over points into (partial) preferences over sets of points in a rational manner is an old task. It started many years ago [14]. This important notion has been considered in logical frameworks [30,47]. Perhaps the most common way, in the finite case (when X is finite), is through a probability p defined on X, which extends additively to subsets of X. Thus, one can define what is called a likelihood probabilistic relation over subsets of (events of) X: we put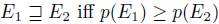 
.
We are considering in this section, in the first place, a way to transfer qualitative information from preferences over points into preferences over sets of points in a very natural manner that goes back to Shackle [44,45] (and has been proposed in various formats by Lewis, Zadeh, Dubois, Spohn, Halpern, etc.). It is called a comparative possibility measure and corresponds to our definition of lifting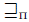 
below. There are other specific and well known liftings in the literature of manipulability, among them we have to mention the liftings of Fishburn [24], Gardenfors [26] and Kelly [31]. They will be defined below.
Let us now turn to the lifting notion:
Definition 3.1. A map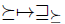 
that sends a preference over 
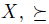, into a partial preference over 
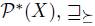, is called a lifting iff the following condition holds for any pair, x, y 
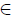X:
Thus if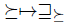 
is a lifting, the partial pre-order 
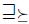is an "extension" of the total pre-order 
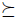. Actually, many liftings have been studied and characterized by Barbera et al. [5]. They call just the property which defines a lifting, the extension property.
We will see that those liftings satisfying the following properties are very interesting for studying manipulation:
Simple Dominance 1 
.
Simple Dominance 2 
.
We call these properties companionship properties because they have a very natural interpretation: Simple Dominance 1 means that the good company improves the group; Simple Dominance 2 means that the bad company worsens the group.
These properties have been widely studied, namely by Barbera et al. in [5]. In that paper many natural liftings have been characterized. It is interesting to notice that among the properties which characterize many liftings we can find the previous properties of Simple Dominance. These properties have been also considered by Geist and Endriss [27] in a work concerning automatized search of impossibility theorems.
Now we are going to give some concrete examples of liftings. The first lifting we introduce is a very standard one: the possibilistic lifting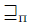 
defined as follows. Let 
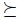be a total pre-order over X. Let A and B be any elements of 
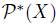. We put
The relation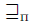 
associated to a relation 
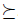, as we said previously, is in fact the comparative possibility relation associated with the "possibility measure" 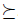(see for instance [19,20]). It extends in a natural way the preferences over elements of X expressed by 
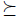, to preferences over 
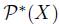expressed by 
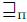. The meaning of A 
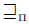B can be stated as follows: A is preferred to B if the best elements of A (related to 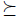) are preferred or indifferent to the best elements of B (related to 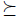); or, even more graphically, that the best elements of A are in a upper level or in the same level than the best elements of B.
Now we define a variant of leximax lifting (see for instance [8,5,16]). In this variant, more precise sets will be preferred. We will call this version the leximax-precise lifting. Suppose |X| = n and consider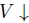 
, the set of all vectors of size less or equal to n, the inputs of which are elements of X ; there are no repetitions of the inputs and finally they are ordered in decreasing manner by 
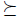. That is, given 
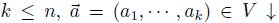iff, for all i, j such that 
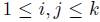with 
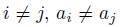and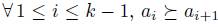 
. Now, given 
, 
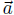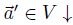of length m with m ≤ n, we define the following relation:
Next we define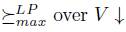 
(where the length of 
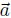vector a is denoted 
)
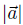Let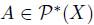 
and suppose that |A| = k. The set of vectors in V 
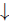of length k with inputs in A will be denoted by R(A), that is
Now we define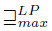 
over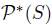 
as follows:
Notice that this definition is not the standard one of leximax; for instance, when we consider the leximax-precise lifting the linear order over a finite set of natural numbers, the vector (4, 3, 2) is preferred (leximax-precise) to the vector (4, 3, 2,1), so the set {2, 3,4} is leximax-precise preferred to the set {1, 2, 3,4}.
It is easy to see that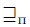 
and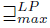 
are total preorders over 
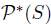. Another interesting lifting considered in many domains, but in particular in Semantics of Programming Languages, is the so called Egli-Milner order [22,39]. It is defined in the following way:
Now we define three well known liftings considered in the literature: Kelly's lifting [31], Fishburn's lifting [24] and Gardenfors' lifting [26]. The Kelly's lifting, denoted by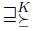 
, is defined as follows:
The Fishburn's lifting, denoted by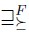 
, is defined as follows:
The Gardenfors' lifting, denoted by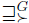 
, is defined as follows: 
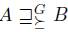if and only if one of the following conditions holds:
(i)
(ii)
(iii)
It is easy to see that these three liftings are in an increasing hierarchy with respect to inclusion. More precisely, we have:
It is also easy to see the following:
Observation 1. The liftings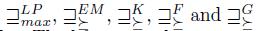 
satisfy the properties Simple Dominance 1 and 2. The lifting 
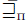does not satisfy the properties Simple Dominance 1 and 2.
Observation 2. There are several natural ways to define liftings. A big number of liftings have been characterized in [5]. Brams and Fishburn [9] discuss the problem of lifting preferences on candidates to sets of candidates. The discussion is in the context of the Approval Voting procedure. The problem of finding the "correct" notion of preference lifting is an extremely important topic for a number of different communities. In this work we will see that we can get an extension of the manipulability theorem for the liftings which have the Companionship properties (Simple Dominance 1 and 2).
4. A manipulability theorem
One of the contributions of this work is the following simple definition:
Definition 4.1. Let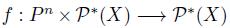 
be a social choice function. f is said to be manipulable (related to a lifting 
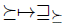) iff there exist 
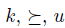, and V such that
Definition 4.2. A social choice function f satisfies the Strong Standard Domain Condition (SSD) if it satisfies the Standard Domain Condition and for all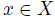 
there exists a profile u such that for all 
.
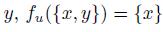This condition means that, for any candidate x, there is a profile u such that for any binary agenda V (that is |V| = 2) containing x, the result is x, in other words, u makes x winner against any other candidate.
It is interesting to note that the Pareto Condition and the Standard Domain Condition imply together the Strong Standard Domain Condition. To see that, it is enough to take as the profile u a profile in which each individual has the alternative x as the most preferred one. Thus, for any individual i and any other alternative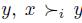 
. Then, by Pareto condition, 
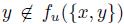and, necessarily, by Standard Domain Condition, 
.
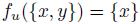Definition 4.3 (Weak Dictator (WD)). A social choice function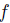 
has a weak dictator k if for all 
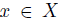, there exists 
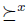such that for all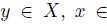 
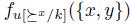
In contrast with the notion of dictator, which is an excluding notion (in the sense that an alternative y will not belong to the result -that is, y will be excluded- if there is an alternative x in the agenda such that, for the dictator, x is preferred to y), the notion of weak dictator is an including one (in the sense that the dictator can choose a preference in order to include an alternative in the result). Of course, if i is a dictator, then i is a weak dictator. To see that, define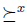 
as a total preorder with x the unique maximal element. Then, it is easy to see that 
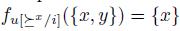, for any 
.
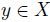The following lemma will be useful in the proof of Theorem 4.5.
Lemma 4.4. Let f be a social choice function satisfying Transitive Explanations and Strong Standard Domain Condition. Then for any x, there exists a profile u such that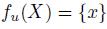 
.
Proof. For a given x, take u such that for all y we have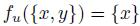 
(the existence of u is guaranteed by SSD). Since f satisfies Transitive Explanations, for any agenda 
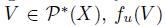is determined by 
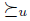in the following way (see Proposition 2.6):
We claim that, by the choice of u, max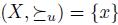 
. Towards a contradiction, suppose this is not the case; therefore, there exists y such that 
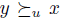; thus max 
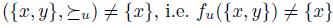, a contradiction. 
Theorem 4.5. Let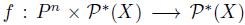 
be a social choice function satisfying the Strong Standard Domain Condition (SSD) and Transitive Explanations (TE). Let
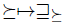be a lifting satisfying the properties of Simple Dominance 1 and 2. Then, related to this lifting,
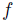is manipulable or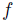has a Weak Dictator.
Before giving a direct proof of this Theorem, we state Barberà-Kelly's Theorem [3,31] (Theorem 5.2.1 in [46]) and we show how Theorem 4.5 can be obtained as a consequence of Barberà-Kelly's Theorem. In order to understand the meaning of this theorem we need some concepts concerning a social choice function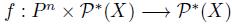 
:
Quasitransitivity: For a profile u, define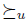 
by letting 
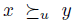iff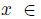 
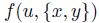. The function 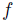is quasitransitive if the strict relation 
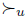associated to 
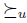is transitive.
Pairwise non-imposed: f is pairwise non-imposed if for every pair of alternatives x, y there exists a profile u such that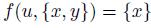 
.
Weak-dominance manipulability: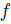 
is weak-dominance manipulable on the agenda V if there is a profile u, an individual i and a preference 
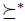such that 
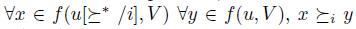and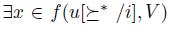 
.
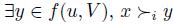Pairwise oligarchy: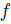 is a pairwise oligarchy if there exists a subset S (the oligarchy) of N such that for every pair 
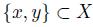we have:
Now we are ready to state the Barberà-Kelly Theorem:
Theorem 4.6.
Let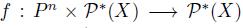
be a social choice function satisfying the following properties:
(i)
is quasitransitive;
(ii)
(iii)
Thenis a pairwise oligarchy.
Our notion of Transitive Explanations entails the notion of quasitransitive; the notion of Strong Standard Domain Condition entails the notion of pairwise non-imposed and finally the notion of non-manipulability by liftings satisfying condition of Simple Dominance 1 and 2 entails the non-manipulability in the sense of weak domination for two-element agendas. Thus, by Barberà-Kelly Theorem, a social choice function satisfying the hypothesis of Theorem 4.5 is a pairwise oligarchy. Say that S is the oligarchy. Notice that any element i in the oligarchy S is a weak dictator. Thus, Theorem 4.5 is actually a consequence of Theorem 4.6. However, the notion of manipulability based on liftings is interesting in itself: Theorem 4.5 gives sufficient conditions on the liftings in order to have a manipulability result.
Direct proof of Theorem 4.5: Let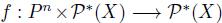 
be a social choice function satisfying SSD and TE. Let 
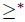be a linear order over X fixed for the rest of the proof.
Define 
by putting
It is clear that g is a voting scheme. From Lemma 4.4 it follows easily that g satisfies the Gibbard Standard Domain Condition. Thus, by Theorem 2.5, g has a Gibbard Dictator or g is manipulable.
Now, in order to finish the proof it is enough to show that the following two remarks hold:
Remark 4.7. If g has a Gibbard Dictator, then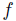 
has a Weak Dictator.
Proof.
Assume that g has a Gibbard Dictator. By the hypothesis there exists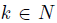 
(the Gibbard Dictator) such that for any 
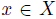, there exists 
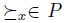such that for any u
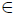Pn we have
that is to say,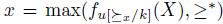 
. Thus, 
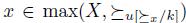. Necessarily, 
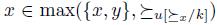, that is 
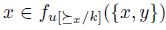. Therefore k is also a Weak Dictator for 
. 
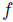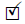
Remark 4.8. If g is manipulable then f is manipulable.
Proof. Assume g is manipulable. Then, there exists a manipulation situation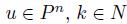 
, and 
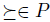such that
Define x and y by the following two equations: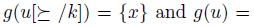 
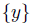. It will be enough to verify the following statement
Notice that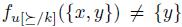 
. If this is not the case, by Transitive Explanations, we should have 
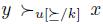and therefore 
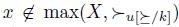. Thus, by Transitive Explanations again, 
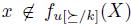and therefore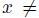 
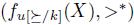, that is, 
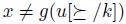, a contradiction. In a similar way, we can see that 
.
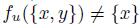Consequently, there are only four possible cases according to the image of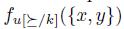 
and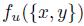 
:
The case (b) & (d) is clearly impossible. The rest of the cases, i.e. (a) & (c), (a) & (d) and (b) & (c) are possible. Let us examine the case (a) & (d). To see that the statement (3) is true, it is enough to verify {x}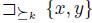 
. By definition of x and y and the statement (2), 
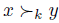. Thus, by Simple Dominance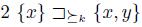 
Now, let us examine the case (a) & (c). Again, by definition of x and y and the statement (2),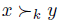 
. Thus, by the extension property, 
.
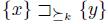For the case (b) & (c), we have, by definition of x and y and the statement (2),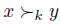 
. Thus, by Simple Dominance 1, 
.
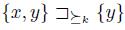We have shown that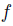 
is manipulable. 
We have, in particular, the following:
Observation 3. Notice that if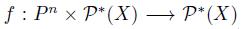 
is a social choice function satisfying the Strong Standard Domain Condition (SSD) and Transitive Explanations (TE), then f has a weak dictator or f is manipulable with respect to the leximax-precise lifting, the Egli-Milner lifting, the Fishburn lifting, the Gardenfors lifting, and the Kelly lifting.
Let us finish this Section with an example illustrating some of the previous results.
Theorem 4.5 shows that the class of manipulable social choice functions is very big. This could be disappointing. However, manipulation is not always seen as a bad property. For a deep discussion about this issue see [15].
Example 4.9. Let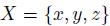 
and N = {1, 2, 3}. We define a social choice function 
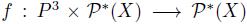, the Borda rule, as follows. First, for each preference 
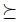and any 
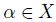we define the Borda rank of 
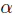relative to 
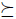, denoted 
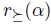, as the level in which 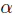appears in the pre-order 
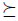For instance, if 
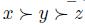we have 
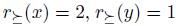and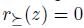 
. We extend additively this notion to profiles. More precisely, if the profile u is 
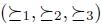, we define 
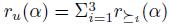. For instance, if
then 
.
We can associate to a profile u, a preference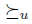 
by putting 
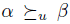iff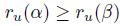 
. It is very easy to prove that 
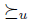is a preference. Finally, we put 
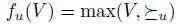. Thus, for instance, for the previously u defined, we have
and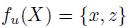 
. So, this function is not generating a voting scheme g via the equation 
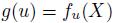. Nevertheless, this function satisfies four of the five properties of Arrow's Theorem (Theorem 2.2). The only property which does not hold is the Independence of Irrelevant Alternatives.
Now if you are calling a wise man to solve conflicts you can have a voting scheme. In order to do that, fix a linear order (the wise man) ≥* over X and put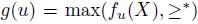 
. It is not hard to see that this g is a voting scheme satisfying the Gibbard Standard Condition and g does not have a weak dictator, so by virtue of Gibbard-Satterthwaite's Theorem (Theorem 2.5), g is manipulable. Actually, if 
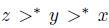and u is defined as before, we have 
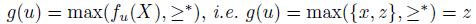and if
Then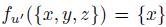 
, so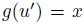 
. But if we denote by 
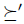the relation satisfying 
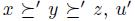is in fact 
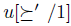. But remember that in the true preferences of individual 1 (the first projection of u) we have 
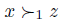, so
that is, the triple 1, u and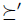 
is a situation of manipulation for g. Thus, the individual 1, by lying, obtains a result which he really prefers.
Note also that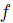 
is manipulable in the sense of Definition 4.1 for any lifting 
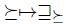satisfying Simple Dominance 2. In order to see that, take V = {x, z}. Because of the shape of 
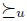and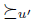 
, it is easy to see that 
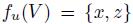and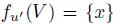 
. Then, by Simple Dominance 2, 
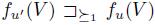. Thus, the individual 1 can also manipulate 
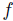. This illustrates Theorem 4.5, that is, 
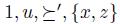is a situation of manipulation for / with respect to any lifting 
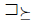satisfying Simple Dominance 2:
This example can have an amusing interpretation: suppose that N is a set of three expert referees evaluating a paper for a conference; x is acceptation, y is revision and z is rejection. If the profile of preferences about the paper is expressed by u and the wise man is the following strict editorial policy of the Committee of Program: the first choice is rejection, the second choice is revision and the least preferred option is acceptation. The paper will be rejected if the procedure adopted is g; but if the first referee considers that the paper has to be accepted, he can change his preferences to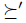 
and then the review result will change favorably to him: the paper will be accepted.
5. Related works
As we have seen in Section 4, our result is a corollary of Barberà-Kelly's Theorem. For a very complete survey about manipulability one can see the book of Alan D. Taylor [46] and the work of Salvador Barbera in the Handbook of Social Choice and Welfare [4]. Nevertheless, we have to point out that our result is new.
Concerning Kelly's lifting, which is one of the liftings satisfying the Dominance conditions, Brandt [10] proves that the social choice functions which are Condorcet extensions are manipulable. It is interesting to compare this result with some consequences of our Theorem 4.5. Note that Theorem 4.5 entails that the social choice functions which do not admit a weak dictator and satisfy strong standard domain condition and transitive explanations are manipulable. Note that the social choice functions which are Condorcet extensions do not admit a weak dictator. Therefore, we obtain from Theorem 4.5 that the social choice functions which are Condorcet extensions and satisfy strong standard domain condition and transitive explanations are manipulable with respect to the Kelly lifting. This is a result which is weaker than Brandt's result. However, we can state our previous corollary in all its generality, that is:
Corollary 5.1. The social choice functions which are Condorcet extensions and satisfy strong standard domain condition and transitive explanations are manipulable with respect to all the liftings satisfying dominance conditions.
The previous corollary is not comparable with Brandt's result in [10].
Brandt and Brill [11] give sufficient conditions in order to have strate-gyproofness with respect the liftings of Kelly, Fishburn and Gardenfors. Putting together their results with Theorem 4.5 we obtain some information. In particular, the social choice functions which are not weak dictatorial and satisfy strong standard domain condition and transitive explanations, fail to satisfy all conditions given by Brandt and Brill in order to have strategyproofness with respect to the liftings of Kelly, Fishburn and Gardenfors.
Interesting links have been found between Social Choice Theory and Judgement Aggregation, see for instance the work of Grossi [29]. A natural question is to search for an interpretation of our Theorem 4.5 in the framework of Judgement Aggregation.
6. Concluding remarks
Let us call the two step approach to social choice the following way to calculate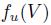 
in two steps: first calculate a sort of aggregation preference 
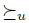and, second, calculate the maximal elements of V with respect to the preference As we already saw, when / satisfies Transitive Explanations, 
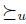can be computed in such a way (cf. Proposition 2.6). Actually, given Proposition 2.6, the second step could seem superfluous because all information is encoded in 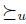. However, the first remark after the results of previous Sections (in particular the weak result about manipulation, Theorem 4.5) is that the whole two step approach to Social Choice is fruitful and far from being superfluous. This new freedom degree -the agenda-together with the concept of lifting allow to define manipulability in a very natural way. Then, also in a very natural way, we can prove a manipulation theorem (we almost can say we lift the Gibbard-Satterthwaite's Theorem -Theorem 2.5).
Concerning this two step approach, it may be worth noting that it appears in Belief Merging under Integrity Constraints [34]. Actually, in that setting there are representation theorems very close to Proposition 2.6. Once more, we insist on the fact that what allows us to state these representation theorems is the explicit role of integrity constraints, the agendas in the framework of Social Choice, see [35].
Incorporating the agenda allowed us to give a different view of manipulability. Actually, a completely different one from those in which you need to have a ternary relation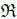 
, such that 
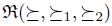means that preference 
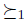is closer to 
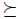than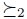 
.
A by-product of this work has been to show clearly the big difference between voting schemes, social choice functions and social choice correspondences.
We list below some possibilities for future work.
To find more general manipulation theorems. As well with the agenda (the two step approach) as without it, i.e. with only the encoding
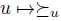(one step approach). Some initial steps in this direction can be found in [37].To characterize the liftings for which Theorem 4.5 holds.
To characterize the relations of closeness for which a manipulation theorem holds.
