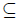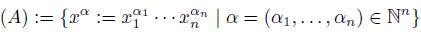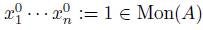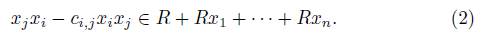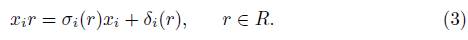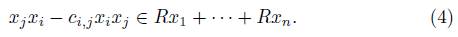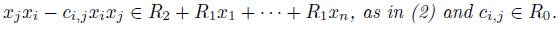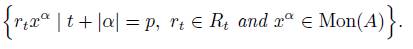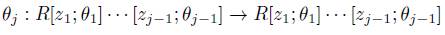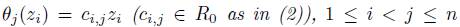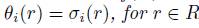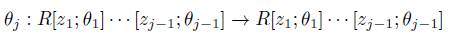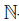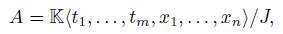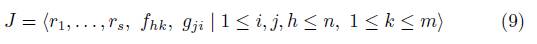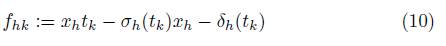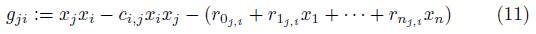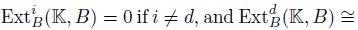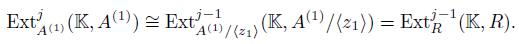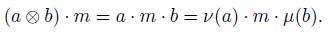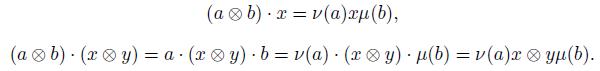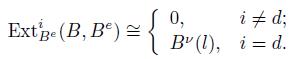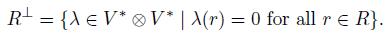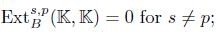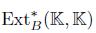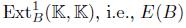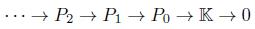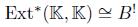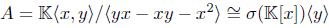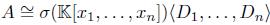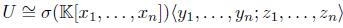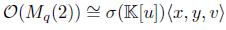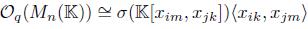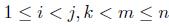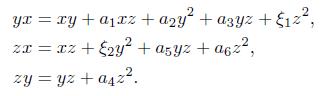1. Introduction
In the schematic approach to non-commutative algebraic geometry, some important classes of non-commutative algebras like Koszul algebras, Artin-Schel-ter regular algebras, Calabi-Yau algebras (see for example [3,4,5,6,10,14,34]) arise, and related with them, the skew PBW extensions (see [18,20]). Koszul algebras were introduced by Priddy in [22]; regular algebras were defined by Artin and Schelter in [3] and they are now known in the literature as Artin-Schelter regular algebras (we denote these algebras in short as AS-regular algebras); Calabi-Yau algebras were defined by Ginzburg in [10], and as a generalization of them, were defined the skew (also named twisted) Calabi-Yau algebras. Skew PBW extensions were introduced in [8]. The first author in [36] defined the graded skew PBW extensions and showed that if R is a finite presented Koszul algebra, then every graded skew PBW extension of R is Koszul. The class of graded skew PBW extensions is more general that the class of graded iterated Ore extensions, for example, the homogenized enveloping algebra  and the diffusion algebra are graded skew PBW extensions but these are not iterated Ore extensions. In [37] were illustrated through examples, known in the literature, some relationships between Koszul algebras, AS-regular algebras, Calabi-Yau algebras and the skew PBW extensions. Formally, there are some relationships between the above algebras, for example:
and the diffusion algebra are graded skew PBW extensions but these are not iterated Ore extensions. In [37] were illustrated through examples, known in the literature, some relationships between Koszul algebras, AS-regular algebras, Calabi-Yau algebras and the skew PBW extensions. Formally, there are some relationships between the above algebras, for example:
(1) Connected graded Calabi-Yau algebras are AS-regular (see [12]).
(2) For connected algebras, skew Calabi-Yau algebras and AS-regular algebras match ([33], Lemma 1.2).
(3) Semi-commutative skew PBW extensions of a field are Koszul algebras ([39], Corollary 3.13).
(4) Graded skew PBW extensions of finitely presented Koszul algebras are Koszul ([36], Theorem 5.5).
We will prove that graded skew PBW extensions of a finitely presented connected Auslander-regular algebra are skew Calabi-Yau. Reyes, Rogalski and J. Zhang in [33] proved that for connected algebras, skew Calabi-Yau property is equivalent to AS-regular property, therefore, graded quasi-commutative skew PBW extensions of connected skew Calabi-Yau algebras are skew Calabi-Yau. We will also show that graded skew PBW extensions of Auslander-regular algebras are skew Calabi-Yau. Moreover, it is clear that Calabi-Yau algebras are skew Calabi-Yau, but we will exhibit examples of graded skew PBW extensions which are skew Calabi-Yau, but not Calabi-Yau (one of them is the Jordan Plane).
2. Graded skew PBW extensions
In this section we present some definitions, properties and examples related with skew PBW extensions. For more details and to check other recent properties related to skew PBW extensions, see [1,2,9,7,17,18,19,23,24,26,25,27,37,16], [28,29,30,31,36,38], [39,40], and [32].
Definition 2.1. Let R and A be rings. We say that A is a skew PBW extension of R if the following conditions hold:
(ii) there exist finitely many elements
A such that A is a left free R-module, with basis the set of standard monomials
(iii) For each 1 ≤ i ≤ n and any r
R \ {0}, there exists an element
such that
(iv) For 1 ≤ i, j ≤ n there exists 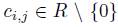 such that
such that
Under these conditions we will write 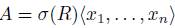 .
.
Proposition 2.2 ([8], Proposition 3). Let A be a skew PBW extension of R. For each 1 ≤ i ≤ n, there exists an injective endomorphism 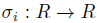 and
and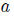
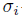 -derivation
-derivation 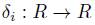 such that
such that
The notation  and the name of skew PBW extensions are due to Proposition 2.2.
and the name of skew PBW extensions are due to Proposition 2.2.
Definition 2.3. Let A be a skew PBW extension of 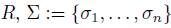 and
and 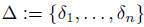 , where
, where 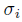 and
and 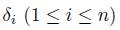 are as in Proposition 2.2.
are as in Proposition 2.2.
(a) A is called pre-commutative if the conditions (iv) in Definition 2.1 are replaced by:
For any 1 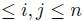 , there exists
, there exists 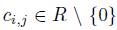 such that
such that
(b) A is called quasi-commutative if the conditions (iii) and (iv) in Definition 2.1 are replaced by
(iii’)for each 1 ≤ i ≤ n and all 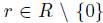 , there exists
, there exists 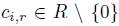 such that
such that
(iv') for any 1 ≤ i, j ≤ n, there exists 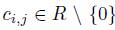 such that
such that
(c) A is called bijective if 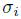 is bijective for each
is bijective for each 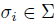 , and
, and 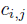 is invertible for any 1 ≤ i ≤ j ≤ n.
is invertible for any 1 ≤ i ≤ j ≤ n.
(d) If 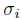 = id
R
for every
= id
R
for every 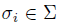 , we say that A is a skew PBW extension of derivation type.
, we say that A is a skew PBW extension of derivation type.
(e) If 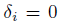 for every
for every 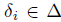 , we say that A is a skew PBW extension of endomorphism type.
, we say that A is a skew PBW extension of endomorphism type.
(f) Any element r of R such that 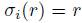 and
and 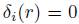 for all 1 ≤ i ≤ n, will be called a constant. A is called constant if every element of R is constant.
for all 1 ≤ i ≤ n, will be called a constant. A is called constant if every element of R is constant.
(g) A is called semi-commutative if A is quasi-commutative and constant. Examples of the above classes of skew PBW extensions can be found in [39].
For the rest of the paper, we fix a field 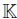 , all algebras are
, all algebras are 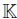 -algebras and the dimension of a
-algebras and the dimension of a 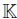 -vector space is denoted by dim
-vector space is denoted by dim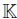 . Let
. Let 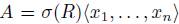 be a skew PBW extension and let
be a skew PBW extension and let 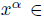 Mon(A) with
Mon(A) with 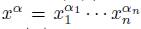 such that
such that  , then we establish the notation
, then we establish the notation 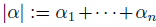 .
.
Proposition 2.4 ([36], Proposition 2.7). Let 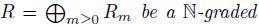 algebra and let
algebra and let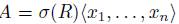 be a bijective skew PBW extension of R satisfying the following two conditions:
be a bijective skew PBW extension of R satisfying the following two conditions:
(i)  is a graded ring homomorphism and
is a graded ring homomorphism and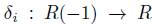 is a graded
is a graded derivation for all 1 ≤ i ≤ n, where
derivation for all 1 ≤ i ≤ n, where  and
and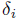 are as in Proposition 2.2.
are as in Proposition 2.2.
For p ≥ 0, let Ap the 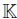 -space generated by the set
-space generated by the set
Then A is 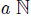 -graded algebra with graduation
-graded algebra with graduation
Definition 2.5. Let 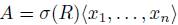 be a bijective skew PBW extension of a
be a bijective skew PBW extension of a 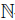 -graded algebra
-graded algebra 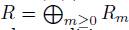 . We say that A is a graded skew PBW extension if A satisfies the conditions (i) and (ii) in Proposition 2.4.
. We say that A is a graded skew PBW extension if A satisfies the conditions (i) and (ii) in Proposition 2.4.
Proposition 2.6. Quasi-commutative skew PBW extensions with the trivial graduation of R are graded skew PBW extensions. If we assume that R has a different graduation from the trivial graduation, then A is a graded skew PBW extension if and only if 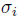 is graded and
is graded and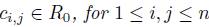 .
.
Proof. Let R = R0 and r 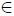 R = R0. From (5) we have that
R = R0. From (5) we have that 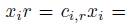
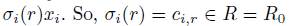 and
and 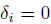 , for 1 ≤ i ≤ n. Therefore
, for 1 ≤ i ≤ n. Therefore 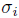 is a graded ring homomorphism and
is a graded ring homomorphism and 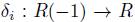 is a graded
is a graded 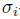 -derivation for all 1 ≤ i ≤ n. On the other hand, from (6) we have that
-derivation for all 1 ≤ i ≤ n. On the other hand, from (6) we have that 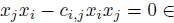
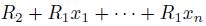 and
and 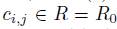 . If R has a nontrivial graduation, then we get the result from relations (5), (6) and Definition 2.5.
. If R has a nontrivial graduation, then we get the result from relations (5), (6) and Definition 2.5. 
An algebra is called Noetherian if it is right and left Noetherian. It is known that a graded algebra A is right (left) Noetherian if and only if it is graded right (left) Noetherian, which means that every graded right (left) ideal is finitely generated ([15], Proposition 1.4).
Proposition 2.7. Let 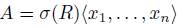 be a graded skew PBW extension.
be a graded skew PBW extension.
(i) If R is a graded (left) Noetherian algebra, then every graded skew PBW extension A of R is graded ( left) Noetherian.
(ii) If A is quasi-commutative, then A is isomorphic to a graded iterated Ore extension of endomorphism type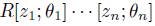 , where
, where 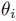 is bijective, for each
is bijective, for each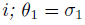 ;
;
Proof. (i) Since A is bijective, then by [19] Corollary 2.4, we have that A is a (left) Noetherian algebra. As A is graded then A is graded left Noetherian.
(ii) By [19], Theorem 2.3 and its proof, we have that A is isomorphic to an iterated Ore extension of endomorphism type 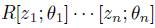 , where
, where 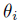 is bijective;
is bijective; 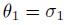 ;
;
is such that 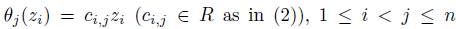 and
and 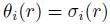 , for
, for 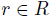 . Since A is graded then oi is graded and
. Since A is graded then oi is graded and 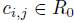 .
.
Moreover, since 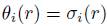 , then
, then 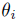 is a graded automorphism for each i. Note that z
i
has graded 1 in A, for all i. Thus,
is a graded automorphism for each i. Note that z
i
has graded 1 in A, for all i. Thus, 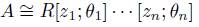 is a graded iterated Ore extension.
is a graded iterated Ore extension. 
Example 2.8. Examples of graded skew PBW extensions can be found in [36]; we present next some examples of graded quasi-commutative skew PBW extensions.
(1) The Sklyanin algebra is the algebra 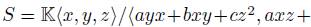
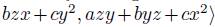 , where
, where 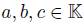 . If
. If 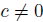 then S is not a skew PBW extension. If c = 0 and
then S is not a skew PBW extension. If c = 0 and  then in
then in 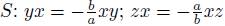 and
and 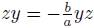 , therefore
, therefore 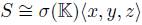 is a skew PBW extension of
is a skew PBW extension of  , and we call this algebra a particular Sklyanin algebra. The particular Sklyanin algebra is a graded quasi-commutative skew PBW extension of
, and we call this algebra a particular Sklyanin algebra. The particular Sklyanin algebra is a graded quasi-commutative skew PBW extension of  .
.
(2) For a fixed 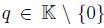 , the algebra of linear partial q-dilation operators with polynomial coefficients is
, the algebra of linear partial q-dilation operators with polynomial coefficients is 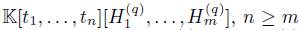 , subject to the relations:
, subject to the relations: 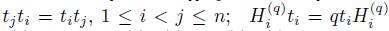
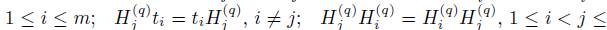 , m. This algebra is a graded quasi-commutative skew PBW extension of
, m. This algebra is a graded quasi-commutative skew PBW extension of 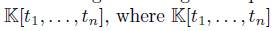 is endowed with the usual graduation.
is endowed with the usual graduation.
(3) The multiplicative analogue of the Weyl algebra is the algebra generated by
is the algebra generated by 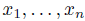 subject to the relations:
subject to the relations: 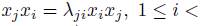
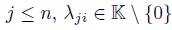 . Thus
. Thus 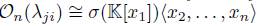 .
.
(4) Let n ≥ 1 and q be a matrix 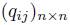 with entries in a field
with entries in a field 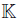 , where
, where 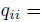
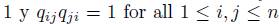 . Then multi-parameter quantum affine n-space
. Then multi-parameter quantum affine n-space 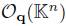 is defined to be the
is defined to be the 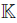 -algebra generated by
-algebra generated by 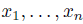 with the relations
with the relations 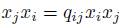 , for all
, for all 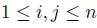 .
.
Remark 2.9. The algebra of shift operators is defined by 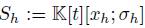 , where
, where 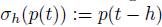 , with
, with 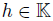 and
and 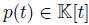 . Notice that
. Notice that 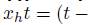
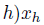 and
and 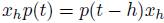 . Thus,
. Thus, 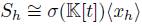 is a quasi-commutative skew PBW extension of
is a quasi-commutative skew PBW extension of 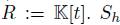 is a graded quasi-commutative skew PBW extension if
is a graded quasi-commutative skew PBW extension if 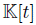 is endowed with trivial graduation. But if
is endowed with trivial graduation. But if 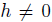 and
and 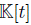 is endowed with the usual graduation, i.e.
is endowed with the usual graduation, i.e. 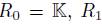 is the subspace generated by t, R
2 is the subspace generated by t
2, etc., then S
h
is not a graded skew PBW extension, since
is the subspace generated by t, R
2 is the subspace generated by t
2, etc., then S
h
is not a graded skew PBW extension, since 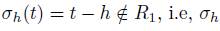 is not graded.
is not graded.
Proposition 2.10.
Let B be connected
connected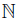 -graded algebra. B is finitely generated as algebra if and only if
-graded algebra. B is finitely generated as algebra if and only if 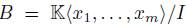 , where I is a proper homogeneous two-sided ideal of
, where I is a proper homogeneous two-sided ideal of 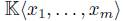 . Moreover, for every
. Moreover, for every 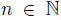 , dim
, dim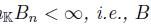 is locally finite.
is locally finite.
Let B be a finitely graded algebra; it is said that B is finitely presented if the two-sided ideal I of relations in Proposition 2.10 is finitely generated.
Remark 2.11. Let 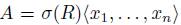 be a graded skew PBW extension, we recall next some properties of A derived from the definition (see [36], Remark 2.10):
be a graded skew PBW extension, we recall next some properties of A derived from the definition (see [36], Remark 2.10):
(ii) R is connected if and only if A is connected.
(iii) If R is finitely generated then A is finitely generated.
(iv) For (i), (ii) and (iii) above we have that if R is a finitely graded algebra (see [34]), then A is a finitely graded algebra.
(v) If R is locally finite, A as algebra is locally finite.
(vi) If A is quasi-commutative and R is concentrated in degree 0, then A0 = R.
(vii) If R is finitely presented then A is finitely presented. Indeed: by Proposition 2.10,
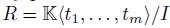 where
where
is a two-sided ideal of 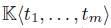 generated by a finite set r1,..., rs of homogeneous polynomials in
generated by a finite set r1,..., rs of homogeneous polynomials in  . Then
. Then
where
is the two-sided ideal of 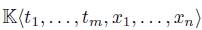 generated by a finite set of homogeneous elements
generated by a finite set of homogeneous elements 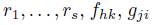 where r1,..., rs are as in (8);
where r1,..., rs are as in (8);
with 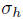 and
and 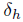 as in Proposition 2.2;
as in Proposition 2.2;
as in (2) of Definition 2.1.
(viii) The class of graded iterated Ore extensions is strictly contained in the class of graded skew PBW extensions (see [36], Remark 2.11).
3. Artin-Schelter regular algebras
Let B be a ring and let M be a B-module. We let pdB (M) denote the pro-jective dimension of M and injdimB (M) the injective dimension of M. Let lgld(B) (rgld(B)) be the left (right) global dimension of B. Not always the left and right global dimensions of B are equal. However, if the ring B is Noetherian the equality holds. If B is Noetherian and if injdim(B B) < 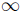 and injdim(BB) <
and injdim(BB) < 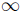 , then injdim(BB) = injdim(BB). We say that B has finite global dimension (resp. finite injective dimension) if the left and right global dimensions of B are finite and equal (resp. the modules BB and BB have finite injective dimensions which are equal). In such case we denote these numbers by gld(B) (resp. injdim(B)).
, then injdim(BB) = injdim(BB). We say that B has finite global dimension (resp. finite injective dimension) if the left and right global dimensions of B are finite and equal (resp. the modules BB and BB have finite injective dimensions which are equal). In such case we denote these numbers by gld(B) (resp. injdim(B)).
Let M be a B-module. The grade number of M is 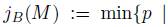
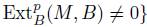 or
or 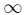 if no such p exists. Notice that
if no such p exists. Notice that 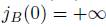 . When B is Noetherian,
. When B is Noetherian, 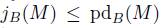 , and if furthermore injdim(B) = q <
, and if furthermore injdim(B) = q < 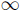 , we have
, we have  for all non-zero finitely generated B-module M (see [15]). A graded ring B has finite graded injective dimension q if B B and BB are both of injective dimension q in the category of graded B-modules. We then write grinjdim(B) = q. If M and N are graded B-modules, we use
for all non-zero finitely generated B-module M (see [15]). A graded ring B has finite graded injective dimension q if B B and BB are both of injective dimension q in the category of graded B-modules. We then write grinjdim(B) = q. If M and N are graded B-modules, we use 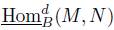 to denote the set of all B-module homomorphisms h: M
to denote the set of all B-module homomorphisms h: M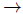 N such that
N such that 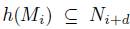 . We set
. We set 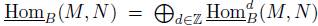 , and we denote the corresponding derived functors by
, and we denote the corresponding derived functors by 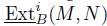 . Given any graded B-module M, for the graded case, the grade number (j-number) of M
. Given any graded B-module M, for the graded case, the grade number (j-number) of M  if no such p exists. In particular, if M = 0, then j
B
(M) = 0. For finitely graded algebras, we have two additional remarks: Let B be a finitely graded algebra and let M, N be
if no such p exists. In particular, if M = 0, then j
B
(M) = 0. For finitely graded algebras, we have two additional remarks: Let B be a finitely graded algebra and let M, N be 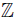 -graded B-modules. Then there is a natural inclusion
-graded B-modules. Then there is a natural inclusion 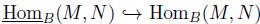 . If M is a B-module finitely generated, then
. If M is a B-module finitely generated, then 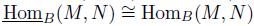 and
and 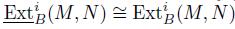 .
.
Definition 3.1 ([15], Definition 2.1). Let B be a Noetherian ring.
(i) A B-module M satisfies the Auslander-condition, if
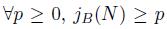 for all B-submodules N of
for all B-submodules N of 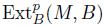
(ii) The ring B is said to be Auslander-Gorenstein of dimension q, if injdim(B) = q <
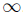 , and every left or right finitely generated B-module satisfies the Auslander-condition.
, and every left or right finitely generated B-module satisfies the Auslander-condition.(iii) The ring B is said to be Auslander-regular of dimension q if gld( B) = q <
 and every left or right finitely generated B-module satisfies the Auslander-condition.
and every left or right finitely generated B-module satisfies the Auslander-condition.(iv) Let B be an algebra. If GKdim(B) = j B (M)+GKdim(M) for every nonzero Noetherian B-module M, then B is called Cohen-Macaulay.
For the case of graded modules, in Definition 3.1, one can define the notion of a graded-Auslander-Gorenstein ring, or graded-Auslander-regular ring. The Noetherian graded ring B is Auslander-Gorenstein (resp. regular) if and only if B is graded-Auslander-Gorenstein (resp. regular) (see [15], Theorem 3.1). Let B be a graded Noetherian ring and let grgld(B) and grinjdim(B) be a graded global dimension and graded injective dimension of B respectively. It is known that gld(B) (resp. injdim(B)) is finite if and only if grgld(B) (resp. grinjdim(B)) is finite. Furthermore we have bounds: grinjdim(B) ≤ injdim(B) ≤ grinjdim(B) + 1 (see [15], p. 281). Let B be a positively graded Noetherian ring. Then injdim(B) <  if and only if grinjdim(B) <
if and only if grinjdim(B) <  , in which case these two numbers are equal (see [15], Lemma 3.3). When B is graded, one can define a graded Cohen-Macaulay property by taking M ≠ 0 as a graded finitely generated B-module.
, in which case these two numbers are equal (see [15], Lemma 3.3). When B is graded, one can define a graded Cohen-Macaulay property by taking M ≠ 0 as a graded finitely generated B-module.
Definition 3.2. Let 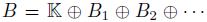 · · be a finitely presented graded algebra over a field
· · be a finitely presented graded algebra over a field  . The algebra B will be called AS-regular if it has the following properties:
. The algebra B will be called AS-regular if it has the following properties:
Remark 3.3. Let B be an algebra.
Proposition 3.4 ([19], Theorem 4.2). Let A be a bijective skew PBW extension of a ring R. Then lgld(A) 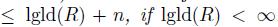 . If A is quasi-commutative, then lgld
. If A is quasi-commutative, then lgld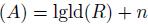 .
.
Proposition 3.5. Let 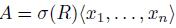 be a graded skew PBW extension of a connected algebra R.
be a graded skew PBW extension of a connected algebra R.
(i) If R is Noetherian with graded finite global dimension, then A has graded finite global dimension and finite GK-dimension.
(ii) If R is graded Auslander-Gorenstein and graded Cohen-Macaulay then A is graded Cohen-Macaulay.
(iii) If R is finitely presented connected Auslander-regular, then A is AS-regular.
Proof.
(i) Since A is a bijective skew PBW extension, then by Proposition 2.7-(i) we have that A is a Noetherian algebra. By Proposition 3.4 we have that lgld(A) < 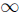 . Now, by Remark 2.11-(ii) we have that A is a connected algebra. So, by Remark 3.3-(ii) we have that GK-dimension of A is finite.
. Now, by Remark 2.11-(ii) we have that A is a connected algebra. So, by Remark 3.3-(ii) we have that GK-dimension of A is finite.
(ii) Since A is bijective, R is a 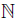 -graded algebra, connected and each
-graded algebra, connected and each 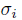 is graded, i.e.,
is graded, i.e., 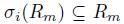 for each m ≥ 0 and 1 ≤ i ≤ n, then by [20], Theorem 3.9, we have that A is Cohen-Macaulay.
for each m ≥ 0 and 1 ≤ i ≤ n, then by [20], Theorem 3.9, we have that A is Cohen-Macaulay.
(iii) Since A is bijective, then by [20], Theorem 2.9, we have that A is Auslander-regular. Now, since R is Noetherian, then by Proposition 2.7-(i) we have that A is Noetherian. Therefore, from [15] Theorem 3.1, we have that A is graded Auslander-regular. From part (i) above, we have that A has graded finite global dimension and finite GK-dimension. Then by [15], Theorem 6.3, we have that A is AS-regular. 
Theorem 3.6. Let R be an AS-regular algebra and let 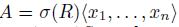 be a graded quasi-commutative skew PBW extension. Then A is AS-regular.
be a graded quasi-commutative skew PBW extension. Then A is AS-regular.
Proof.
Let 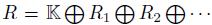 · be an AS-regular algebra and let A be a graded skew PBW extension of A. Since R is finitely presented, then by Proposition 2.10, we know that
· be an AS-regular algebra and let A be a graded skew PBW extension of A. Since R is finitely presented, then by Proposition 2.10, we know that 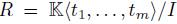 , where I is a proper two-sided ideal of
, where I is a proper two-sided ideal of 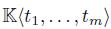 generated by finite homogeneous polynomials r1,...,rs in
generated by finite homogeneous polynomials r1,...,rs in 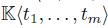 (it is assumed that t
j
has grade 1, 1 ≤ j ≤ m). Then
(it is assumed that t
j
has grade 1, 1 ≤ j ≤ m). Then 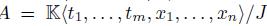 , where J is a two-sided ideal of
, where J is a two-sided ideal of 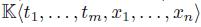 , generated by a finite set of homogeneous polynomials
, generated by a finite set of homogeneous polynomials 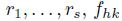 and
and 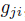 , where the polynomials fhk are as in (10) and g¿¿ are as in (11). Now, by Remark 2.11-(ii), we have that A is connected. So, by Proposition 2.4 and Remark 2.11-(vii), we know that
, where the polynomials fhk are as in (10) and g¿¿ are as in (11). Now, by Remark 2.11-(ii), we have that A is connected. So, by Proposition 2.4 and Remark 2.11-(vii), we know that 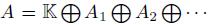 · is a finitely presented graded algebra.
· is a finitely presented graded algebra.
(i) Since R has finite global dimension, say e, then by Proposition 3.4 we know that lgld(A) = e + n = d, i.e., A has finite global dimension.
(ii) Let V be a subspace of R generated by {t1,... , tm}. Note that V is a finite dimensional generating subspace of R. As
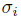 is graded for all i, then
is graded for all i, then 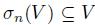 . Now, as A is bijective and R has finite GK-dimension then by [23], Theorem 14, we have that GKdim(A) =GKdim(R) + n, i.e., A has finite GK-dimension.
. Now, as A is bijective and R has finite GK-dimension then by [23], Theorem 14, we have that GKdim(A) =GKdim(R) + n, i.e., A has finite GK-dimension.(iii) From Proposition 2.7-(ii) and his proof, we know that A is isomorphic to a graded iterated Ore extension of endomorphism type
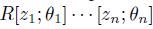 , where
, where 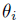 is bijective, for each
is bijective, for each 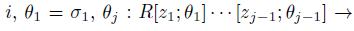
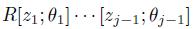 is such that
is such that 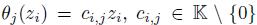 and
and 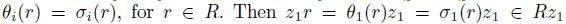 and
and 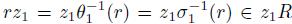 . Hence
. Hence 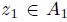 is a nonzero normal element of
is a nonzero normal element of 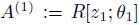 and
and 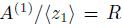 . From the Rees lemma (see [15], Proposition 3.4-(b)) we have that
. From the Rees lemma (see [15], Proposition 3.4-(b)) we have that
By Proposition 3.4, we have that 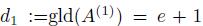 . Since R is Gorenstein. Then
. Since R is Gorenstein. Then 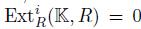 , if
, if 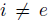 and
and 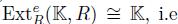
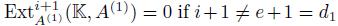
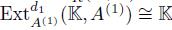 . Then
. Then 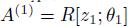 is Gorenstein. Now
is Gorenstein. Now 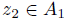 is nonzero normal element of
is nonzero normal element of 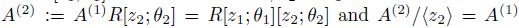 . Thus, with the above procedure we have that
. Thus, with the above procedure we have that 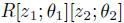 is Gorenstein. Now,
is Gorenstein. Now, 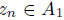 is a nonzero normal element of
is a nonzero normal element of 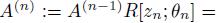
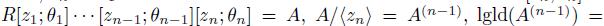
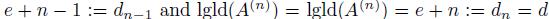 . Assuming that
. Assuming that 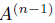 is Gorenstein, we have that
is Gorenstein, we have that 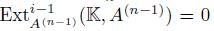
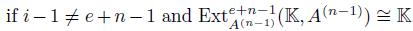 . From the Rees lemma, we have that
. From the Rees lemma, we have that 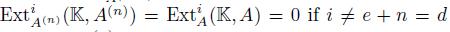 and
and 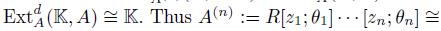 . A is Gorenstein.
. A is Gorenstein.
4. Calabi-Yau algebras
The enveloping algebra of an algebra B is the tensor product 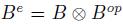 , where Bop is the opposite algebra of B. Bimodules over B are essentially the same as modules over the enveloping algebra of B, so in particular, B and M can be considered as Be-modules. Suppose that M and N are both Be-modules. Then there are two Be-module structures on M
, where Bop is the opposite algebra of B. Bimodules over B are essentially the same as modules over the enveloping algebra of B, so in particular, B and M can be considered as Be-modules. Suppose that M and N are both Be-modules. Then there are two Be-module structures on M  N, one is called the outer structure defined by
N, one is called the outer structure defined by 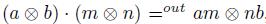 , and the other is called the inner structure defined by
, and the other is called the inner structure defined by 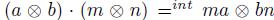 , for any
, for any 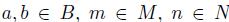 . Since Be is identified with B C B as a
. Since Be is identified with B C B as a 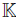 -module
-module 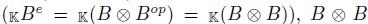 endowed with the outer structure is nothing but the left regular
endowed with the outer structure is nothing but the left regular 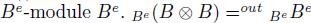 : In
: In 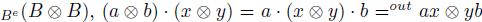 , whereas that in
, whereas that in 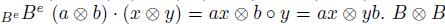 endowed with the inner structure is nothing but the right regular
endowed with the inner structure is nothing but the right regular 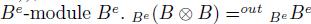 : In
: In 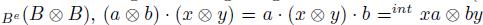 , whereas that in
, whereas that in 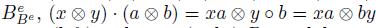 . Hence, we often say Be has the outer (left) and inner (right) Be-module structures.
. Hence, we often say Be has the outer (left) and inner (right) Be-module structures.
An algebra B is said to be homologically smooth, if as a Be-module, B has a projective resolution that has finite length and is such that each term in the projective resolution is finitely generated. The length of this resolution is known as the Hochschild dimension of B. In the next definition, the outer structure on Be is used when computing the homology 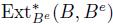 . Thus,
. Thus, 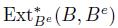 admits a Be-module structure induced by the inner one on Be.
admits a Be-module structure induced by the inner one on Be.
Let M be a B-bimodule, 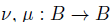 be two automorphisms, the skew B-bimodule
be two automorphisms, the skew B-bimodule 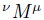 is equal to M as a vector
is equal to M as a vector 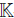 -space with
-space with 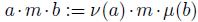 . Thus, M is a left Be-module with product given by
. Thus, M is a left Be-module with product given by
In particular, for B and Be we have the structure of left Be-modules given by
Definition 4.1. A graded algebra B is called skew Calabi-Yau of dimension d if
as Be -modules, for some integerl. If ν is the identity, then B is said to be Calabi-Yau.
Ungraded Calabi-Yau algebras are defined similarly but without degree shift. The automorphism ν is called the Nakayama automorphism of B, and is unique up to inner automorphisms of B. Note that a skew Calabi-Yau algebra is Calabi-Yau if and only if its Nakayama automorphism is inner.
Proposition 4.2 ([33], Lemma 1.2). Let B be a connected graded algebra. Then B is skew Calabi-Yau if and only if it is AS-regular.
A graded algebra is quadratic if 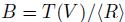 where V is a finite dimensional
where V is a finite dimensional 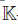 -vector space, concentrated in degree l; T(V) is the tensor algebra on V, with the induced grading, and (R) is the ideal generated by a subspace
-vector space, concentrated in degree l; T(V) is the tensor algebra on V, with the induced grading, and (R) is the ideal generated by a subspace 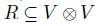 . The dual of such a quadratic algebra is
. The dual of such a quadratic algebra is 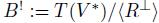 , where
, where
Let 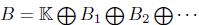 · be a locally finite graded algebra and E(B) =
· be a locally finite graded algebra and E(B) = 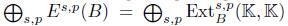 the associated bigraded Yoneda algebra, where s is the cohomology degree and - p is the internal degree inherited from the grading on A. Let
the associated bigraded Yoneda algebra, where s is the cohomology degree and - p is the internal degree inherited from the grading on A. Let 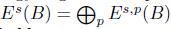 . B is called Koszul if the following equivalent conditions hold:
. B is called Koszul if the following equivalent conditions hold:
such that P i is generated in degree i.
Theorem 4.3 ([36], Theorem 5.5). If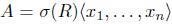 is a graded skew PBW extension of a finitely presented Koszul algebra R, then A is Koszul.
is a graded skew PBW extension of a finitely presented Koszul algebra R, then A is Koszul.
Proposition 4.4. Let R be a Koszul AS-regular algebra of global dimension d with Nakayama automorphism σ.
(i) ([13], Theorem 3.3) The skew polynomial algebra B = R[x; σ] is a Calabi-Yau algebra of dimension d + 1.
(ii) ([41], Remark 3.13) There exists a unique skew polynomial extension B such that B is Calabi-Yau.
(iii) ([41], Theorem 3.16) If ν is a graded algebra automorphism of R, then
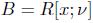 is Calabi-Yau if and only if σ = ν.
is Calabi-Yau if and only if σ = ν.
Note that the Calabi-Yau property is not preserved by skew PBW extensions. The Jordan plane 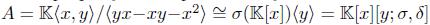 , where
, where 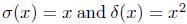 , is a graded skew PBW extension of a Calabi-Yau algebra
, is a graded skew PBW extension of a Calabi-Yau algebra 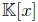 , but A is not Calabi-Yau. Indeed: the Nakayama automorphism ν of the Jordan plane is given by
, but A is not Calabi-Yau. Indeed: the Nakayama automorphism ν of the Jordan plane is given by 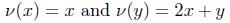 (see for example [21], Page 16) and this is not inner.
(see for example [21], Page 16) and this is not inner.
The Calabi-Yau and skew Calabi-Yau properties for graded skew PBW extensions will be next proved using the cited results presented in the literature and our previous results.
Theorem 4.5.
Let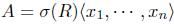 be a graded skew PBW extension of an algebra R.
be a graded skew PBW extension of an algebra R.
(i) If A is quasi-commutative and R is a connected skew Calabi-Yau algebra of global dimension d, then A is skew Calabi-Yau of global dimension d + n. Moreover, if R is Koszul and θ ί is the Nakayama automorphism of
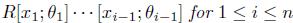 , then A is Calabi-Yau of dimension d + n (θi as in Proposition 2.7-(ii),
, then A is Calabi-Yau of dimension d + n (θi as in Proposition 2.7-(ii), 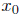 = 1).
= 1).(ii) If R is finitely presented, connected and Auslander-regular, then A is skew Calabi-Yau.
Proof. (i) Since R is connected and skew Calabi-Yau, then by Proposition 4.2 we know that R is AS-regular. From Theorem 3.6 we have that A is AS-regular and, in particular, connected. Thus, using again Proposition 4.2, we have that A is a skew Calabi-Yau algebra. By the proof of Theorem 3.6 we have that the global dimension of A is d + n.
For the second part, we know that graded Ore extensions of Koszul algebras are Koszul algebras and, as a particular case of Theorem 3.6, we have that a graded Ore extension of an AS-regular algebra is an AS-regular algebra. Now, by Proposition 2.7-(ii) we have that A is isomorphic to a graded iterated Ore extension 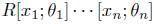 . It is known that if A is a Calabi-Yau algebra of dimension d, then the global dimension of A is d (see for example [6], Remark 2.8). Then, using Proposition 4.4-(i) and applying induction on n we obtain that A is a Calabi-Yau algebra of dimension d + n.
. It is known that if A is a Calabi-Yau algebra of dimension d, then the global dimension of A is d (see for example [6], Remark 2.8). Then, using Proposition 4.4-(i) and applying induction on n we obtain that A is a Calabi-Yau algebra of dimension d + n.
(ii) From Proposition 3.5-(iii) we have that A is AS-regular. Since R is connected, then by Remark 2.11-(ii) we have that A is connected. Then from Proposition 4.2 we get that A is skew Calabi-Yau. 
Using the previous results we have the following examples of skew Calabi-Yau algebras and AS-regular algebras. For some of these algebras other authors had already studied the skew Calabi-Yau property and the Artin-Schelter regularity, but using other techniques. The novelty here consists in interpreting these algebras as skew PBW extensions and applying some its algebraic properties studied before in [19] and [36].
Example 4.6. From Theorem 3.6 we obtain that the algebra of linear partial q-dilation operators 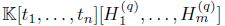 (Example 2.8-2), multiplicative analogue of the Weyl algebra
(Example 2.8-2), multiplicative analogue of the Weyl algebra 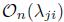 (Example 2.8-3) and multi-parameter quantum affine n-space
(Example 2.8-3) and multi-parameter quantum affine n-space 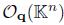 (Example 2.8-4), are AS-regular algebras. By Theorem 4.5-(i), we have that the above examples are also skew Calabi-Yau algebras.
(Example 2.8-4), are AS-regular algebras. By Theorem 4.5-(i), we have that the above examples are also skew Calabi-Yau algebras.
Example 4.7. The following examples are graded skew PBW extensions of the classical polynomial ring R with coefficients in a field 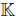 , which are not quasi-commutative and where R has the usual graduation (see [36], Example 2.9). In [8,19] and [38] we can find further details of these algebras. By Theorem 4.5-(ii), these extensions are skew Calabi-Yau algebras, since R is a connected Auslander-regular algebra.
, which are not quasi-commutative and where R has the usual graduation (see [36], Example 2.9). In [8,19] and [38] we can find further details of these algebras. By Theorem 4.5-(ii), these extensions are skew Calabi-Yau algebras, since R is a connected Auslander-regular algebra.
If 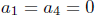 then the quadratic algebra is a graded skew PBW extension of
then the quadratic algebra is a graded skew PBW extension of 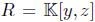 , and if
, and if 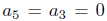 then quadratic algebras are graded skew PBW extensions of
then quadratic algebras are graded skew PBW extensions of 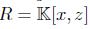 .
.
Note that the above algebras are also AS-regular algebras (see proof of Theorem 4.5-(ii)).
It is possible that for algebras (1) - (7) above, the AS-regular and the skew Calabi-Yau properties may have not been yet studied.
Remark 4.8. Every skew Calabi-Yau algebra may be extended to a Calabi-Yau algebra, i.e., if B is a skew Calabi-Yau algebra then 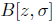 is Calabi-Yau, where σ is the Nakayama automorphism (see [11], Theorem 1.1 and Remark 5.1).
is Calabi-Yau, where σ is the Nakayama automorphism (see [11], Theorem 1.1 and Remark 5.1).