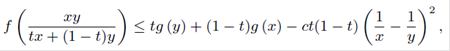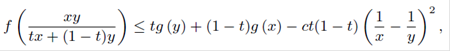Text complete end PDF
Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Colombiana de Matemáticas
versão impressa ISSN 0034-7426
Rev.colomb.mat. vol.52 no.2 Bogotá jul./dez. 2018
https://doi.org/10.15446/recolma.v52n2.77157
Original articles
Sandwich theorem for reciprocally strongly convex functions
Teorema del Sandwich para funciones fuerte-recíprocamente convexas
1 Escuela Superior Politécnica del Litoral (ESPOL) Departamento de Matemáticas, Facultad de Ciencias Naturales y Matemática, Km 30.5 Vía Perimetral, Campus Gustavo Galindo, Guayaquil, Ecuador. e-mail: mirebrac@gmail.com
2 Universidad de los Andes, Departamento de Matemáticas, Facultad de Ingeniería. Mérida, Venezuela. e-mail: jgimenez@ula.ve
3 Universidad Centroccidental Lisandro Alvarado, Departamento de Matemáticas, Decanato de Ciencias y Tecnología. Barquisimeto, Venezuela. e-mail: jesus.medina@ucla.edu.ve
We introduce the notion of reciprocally strongly convex functions and we present some examples and properties of them. We also prove that two real functions f and g, defined on a real interval [a, b], satisfy
for all x, y ∈ [a, b] and t ∈ [0, 1] iff there exists a reciprocally strongly convex function h: [a, b] → R such that f (x) ≤ h(x) ≤ g(x) for all x ∈ [a, b].
Finally, we obtain an approximate convexity result for reciprocally strongly convex functions; namely we prove a stability result of Hyers-Ulam type for this class of functions.
Keywords: Convex functions; Sandwich theorem; Hyers-Ulam
En este artículo introducimos la noción de funciones recíproca-fuertemente convexas y presentamos algunos ejemplos y propiedades. Además se demuestran que dos funciones f y g, definidas en el intervalo real [a, b] satisfacen la desigualdad
para todo x, y ∈ [a, b] y t ∈ [0, 1] si, y sólo si, existe una función recíproca-fuertemente convexa h : [a, b] → R tal que f (x) ≤ h(x) ≤ g (x) para todo x ∈ [a, b].
Finalmente, se obtiene un resultado de aproximación convexa para esta clase de funciones.
Palabras clave: Funciones convexas; Teorema del Sandwich; Hyers-Ulam
References
[1] M. Avriel, W.T. Diewert, S. Schaible, and I. Zang, Generalized concavity, 1998. [ Links ]
[2] K. Baron, J. Matkowski, and K. Nikodem, A sandwich with convexity, Math. Pannica 5/1 (1994), 139-144. [ Links ]
[3] M. Bessenyei and Zs. Páles, Characterization of convexity via Hadamard's inequality, Math. Inequal. Appl. 9 (2006), 53-62. [ Links ]
[4] M. Bracamonte, J. Giménez, and J. Medina, Hermite-Hadamard and Fejér type inequalities for strongly harmonically convex functions, Submitted for publication (2016). [ Links ]
[5] M. Bracamonte, J. Giménez, J. Medina, and M. Vivas, A sandwich theorem and stability result of Hyers-Ulam type for harmonically convex functions, Submitted for publication (2016). [ Links ]
[6] A. Daniilidis and P. Georgiev, Approximately convex functions and approximately monotonic operators, Nonlin. Anal., 66 (2007), 547-567. [ Links ]
[7] S. Dragomir, Inequalities of Hermite-Hadamard type for h-convex functions on linear spaces, Mathematica Moravica (2015), 107-121. [ Links ]
[8] ______, Inequalities of Jensen type for HA-convex functions, RGMIA Monographs, Victoria University (2015). [ Links ]
[9] S. Dragomir and C. Pearce, Selected topics on Hermite-Hadamard inequalities and applications, 2000. [ Links ]
[10] A. Eberhard and Pearce C. E. M., Class inclusion properties for convex functions, in progress in optimization, Appl. Optim, Kluwer Acad. Publ., Dordrecht, 39 (1998), 129-133. [ Links ]
[11] L. Fejér, Über die fourierreihen, II, Math. Naturwiss. Anz Ungar. Akad.Wiss. (1906), 369-390. [ Links ]
[12] A. Ghazanfari and S. Dragomir, Hermite-Hadamard inequality for functions whose derivatives absolute values are preinvex, 2012. [ Links ]
[13] G. H. Hardy, J.E. Littlewood, and G. Polya, Inequalities, Cambridge Univ. Press., 1934. [ Links ]
[14] J. Hiriart-Urruty and C. Lemaréchal, Fundamentals of convex analysis, Springer-Verlag, Berlin-Heidelberg, 2001. [ Links ]
[15] D. H. Hyers, On the stability of the linear functional equations, Proc. Nat. Acad. Sci. USA 27 (1941), 222-224. [ Links ]
[16] D. H. Hyers and S. M. Ulam, Approximately convex functions, Proc. Amer. Math. Soc.3 (1952), 821-828. [ Links ]
[17] I. Iscan, Hermite-Hadamard type inequalities for harmonically (α,m) convex functions, Contemp. Anal. Appl. Math., 1 (2) (2013), 253-264. [ Links ]
[18] I. Iscan, New estimates on generalization of some integral inequalities for s-convex functions and their applications, Int. J. Pure Appl. Math., 86 (4) (2013), 727-726. [ Links ]
[19] I. Iscan, Hermite-Hadamard type inequalities for harmonically convex functions, Hacettepe Journal of Mathematics and Statistics Volume 43 (6) (2014), 935 - 942. [ Links ]
[20] M. V. Jovanovic, A note on strongly convex and strongly quasiconvex functions, Notes 60 (1996), 778-779. [ Links ]
[21] S. M. Jung, Hyers-ulam-rassias stability of functional equations in mathematical analysis, Hadronic Press, Inc., Palm Harbor, 2001. [ Links ]
[22] M. Kuczma, An introduction to the theory of functional equations and inequalities, Cauchy's equation and Jensen's inequality, Second Edition, Birkhäuser, Basel Boston Berlin, 2009. [ Links ]
[23] N. Merentes and K. Nikodem , Remarks on strongly convex functions, Aequationes mathematicae, Volume 80, Issue 1 (2010), 193-199. [ Links ]
[24] F. C. Mitroi-Symeonidis, Convexity and sandwich theorems, European Journal of Research in Applied Sciences, Vol. 1, No. 1 (2015), 9-11. [ Links ]
[25] C. Niculescu and L. Persson, Convex functions and their applications, A Contemporary Approach, CMS Books in Mathematics, vol. 23, Springer, New York, 2006. [ Links ]
[26] K. Nikodem and S. Wasowicz, A sandwich theorem and Hyers-Ulam stability of affine functions, Aequationes Math. 49 (1995), 160-164. [ Links ]
[27] M. A. Noor, K. I. Noor, and M. U. Awan, Some characterizations of harmonically log-convex functions, Proc. Jangjeon Math. Soc., 17(1) (2014), 51-61. [ Links ]
[28] ______, Some integral inequalities for harmonically logarithmic h-convex functions, preprint (2014). [ Links ]
[29] B. Polyak, Existence theorems and convergence of minimizing sequences in extremum problems with restrictions, Dokl. Akad. Nauk. SSSR 166 (1966), 287-290. [ Links ]
[30] A. Roberts and D. Varberg, Convex functions, Academic Press, New York-London, 1973. [ Links ]
[31] R.T. Rockafellar, Monotone operator and the proximal point algorithm, SIAM J. Control Optim 14 (1976), 888-898. [ Links ]
[32] S. M. Ulam, A collection of mathematical problems, Interscience Publ., New York, 1960. [ Links ]
[33] S. Varosanec, On h-convexity, J. Math. Anal. Appl. 326 (2007), 303 - 311. [ Links ]
[34] T.-Y Zhang, A.-P. Ji, and F. Qi, Integral inequalities of Hermite-Hadamard type for harmonically quasiconvex functions, Proc. Jangjeon Math. Soc ., 16(3) (2013), 399-407. [ Links ]
Received: January 31, 2018; Accepted: May 08, 2018