* Profesor Asociado, Departamento del Movimiento Corporal Humano, Instituto de Investigaciones Clínicas, Facultad de Medicina, Universidad Nacional de Colombia. Bogotá (Colombia). Correo electrónico: ecortesr@unal.edu.co

** Profesor Asociado, Departamento de Obstetricia y Ginecología, Instituto de Investigaciones Clínicas, Facultad de Medicina, Universidad Nacional de Colombia. Bogotá (Colombia).

*** Profesor Titular, Departamento de Obstetricia y Ginecología, Instituto de Investigaciones Clínicas, Facultad de Medicina, Universidad Nacional de Colombia. Bogotá (Colombia).

RESUMEN

Introducción: en la evaluación de la utilidad de una prueba diagnóstica, se requiere en algunas situaciones valorar la reproducibilidad de los resultados o la concordancia de los mismos al compararla con otra prueba que no sea usada como patrón de oro de la entidad. El objetivo de este documento es presentar los métodos estadísticos utilizados para evaluar la reproducibilidad y/o concordancia de las observaciones clínicas o paraclínicas, sus bases teóricas y algunos ejemplos de cómo se han aplicado.

Metodología: se realiza una revisión sobre las bases teóricas de la evaluación de la concordancia y la reproducibilidad, además se ilustra su aplicación en la literatura con ejemplos relacionados con la obstetricia y la ginecología.

Resultados: la estimación de la concordancia se hace por medio de la prueba Kappa en variables dicotómicas u ordinales. En el caso de variables continuas, se debe preferir el uso del coeficiente de correlación intraclase o el coeficiente de correlación y concordancia sobre el uso del coeficiente de Pearson o la prueba t de Student pareada. Los métodos utilizados deben ser interpretados de acuerdo al contexto clínico donde fueron empleados.

Conclusiones: la selección de los métodos estadísticos para la evaluación de la concordancia y la reproducibilidad depende del tipo de variable a medir y de los parámetros que se quieran evaluar, ya sea sólo la reproducibilidad o también la exactitud.

Palabras clave: reproducibilidad de resultados, correlación, concordancia, acuerdo.

SUMMARY

Introduction: when evaluating a diagnostic test’s usefulness, one often has to assess the results’ repeatability or their degree of agreement when compared to another test which is not used as gold standard for the entity in question. This paper was aimed at presenting the statistical methods used for evaluating clinical and laboratory observations’ repeatability or reproducibility and agreement, their theoretical basis and showing some examples of how they have been applied.

Methodology: the theoretical bases for evaluating agreement and the repeatability of results were reviewed and examples of their use were taken from pertinent obstetrics- and gynecology-related literature.

Results: the Kappa coefficient is usually used for evaluating the degree of agreement or concordance for dichotomic or categorical variables. The use of the intraclass correlation coefficient (ICC) or Lin’s concordance correlation coefficient should be preferred over Pearson’s correlation coefficient or paired Student’s t-test for assessing continuous variables’ concordance. These methods must be interpreted according to the clinical context in which they were used.

Conclusions: the selection of statistical methods for evaluating agreement and reproducibility depends on the type of variable being measured and on the parameters being evaluated for assessing either reproducibility or validity.

Key words: reproducibility of results, correlation, agreement, concordance.

INTRODUCCIÓN

Para cualquier profesional de la salud, y en particular para el especialista en Obstetricia y Ginecología, puede ser de interés evaluar la utilidad de una prueba diagnóstica, ya sea desde el punto de vista de 1) qué tan bien ésta clasifica al sujeto como sano o enfermo de acuerdo a su real estado de salud, es decir, el desempeño operativo de la prueba (sensibilidad y especificidad)¹ o desde el punto de vista de 2) la confiabilidad de la prueba o la reproducibilidad de los resultados, por ejemplo, al ser nuevamente aplicada por otro sujeto, por el mismo sujeto o al compararla con otra prueba que no es usada como patrón de oro de la entidad o 3) para verificar qué tan de acuerdo están dos observadores frente a un fenómeno. Dos ejemplos en el ejercicio de la actividad diaria son qué tanto varían las mediciones por ultrasonido del grosor endometrial entre dos observadores² o el grado de acuerdo entre dos métodos de biología molecular para el diagnóstico del virus del papiloma humano en mujeres de alto riesgo.³

El presente artículo tiene como objetivo presentar los métodos utilizados para el análisis de los estudios de la reproducibilidad y/o concordancia de las observaciones clínicas o paraclínicas. Se explican sus bases teóricas y se brindan algunos ejemplos de cómo se han aplicado para que el clínico pueda conocer la forma de interpretación de los resultados y si la evaluación de estas características de las pruebas está bien realizada.

El término concordancia se deriva de la expresión latina concordare, cuyo significado hace referencia a que hay ‘correspondencia o conformidad de una cosa con otra’.⁴ Su importancia en el área de la salud reside en que existen diversas maneras de valorar los fenómenos de la naturaleza y por lo tanto aparecen distintas aproximaciones

o métodos diagnósticos usados para medir los mismos fenómenos o enfermedades. Por lo tanto, la concordancia adquiere importancia cuando se desea conocer si con un método o instrumento nuevo, diferente al habitual, se obtienen resultados equivalentes de tal manera que eventualmente uno y otro puedan ser remplazados o intercambiados ya sea porque uno de ellos es más sencillo, menos costoso y por lo tanto más costo-efectivo, o porque uno de ellos resulta más seguro para el paciente, entre otras múltiples razones. En términos generales, la concordancia es el grado en que dos o más observadores, métodos, técnicas u observaciones están de acuerdo sobre el mismo fenómeno observado.⁵

Así, la concordancia no evalúa la validez o la certeza sobre una u otra observación con relación a un estándar de referencia dado, sino cuán acordes están entre sí observaciones sobre el mismo fenómeno. En estos casos se considera que los estudios evalúan la consistencia entre los métodos o instrumentos. En los estudios en los que uno de los métodos o instrumentos nuevos se comparan frente al método que constituye el patrón de referencia o gold estándar, se evalúa la conformidad⁶ del método respecto al patrón de referencia que también se denomina validez o desempeño operativo de una prueba diagnóstica.

La concordancia entre los métodos y sus mediciones puede alterarse por los siguientes elementos o fuentes de error: 1) la variabilidad de los observadores, 2) la variabilidad dada por el instrumento de medida y 3) la variabilidad debida a medir en momentos diferentes en el tiempo.⁷ En un estudio de concordancia se ejerce un efecto artificial de controlar la variabilidad en el fenómeno observado mientras que se determina el grado de acuerdo entre dos o más observadores o instrumentos sobre ese fenómeno.⁸ Ahora bien, es posible que dos o más observaciones u observadores estén de acuerdo, sólo por efecto del azar. Bajo esta premisa, se han diseñado modelos estadísticos que estiman el grado de acuerdo existente entre dos o más observadores u observaciones, después de retirar el efecto del azar de dicha observación.

Concordancia de variables categóricas

En el evento en que el fenómeno observado se expresa o determina de manera binaria o dicotómica, por ejemplo, la presencia o ausencia de un signo clínico o imagenológico,⁹ se ha utilizado tradicionalmente el índice de kappa, un instrumento diseñado por Cohen que ajusta el efecto del azar en la proporción de la concordancia observada.¹⁰ La estimación por el índice de Kappa sigue la ecuación:

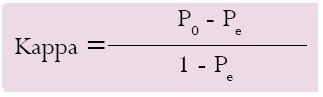
Donde P₀ es la proporción de concordancia observada, P_e es la proporción de concordancia esperada por azar y 1 - P_e, representa el acuerdo o concordancia máxima posible no debida al azar. Entonces, el numerador del coeficiente Kappa expresa la proporción del acuerdo observado menos el esperado, en tanto que el denominador es la diferencia entre un total acuerdo y la proporción esperada por azar. En conclusión, el Kappa corrige el acuerdo sólo por azar, en tanto es la proporción del acuerdo observado que excede la proporción por azar. Si este valor es igual a 1, estaríamos frente a una situación en que la concordancia es perfecta (100% de acuerdo o total acuerdo) y por tanto, la proporción por azar es cero; cuando el valor es 0, hay total desacuerdo y entonces la proporción esperada por azar se hace igual a la proporción observada.

Como ejemplo tenemos que Massad y colaboradores en el 2008,¹¹ estimaron el grado de concordancia entre observadores para calificar el índice de Reid en imágenes colposcópicas previamente seleccionadas, obtenidas del estudio ALTS (Ascus/ LSIL Triage Study). La tabla 1 muestra los resultados obtenidos para la identificación de lesiones acetoblancas por dos observadores independientes y cómo se obtuvo el valor del índice de Kappa de concordancia entre los observadores.

De otro lado, Landis y Koch¹² propusieron una interpretación cualitativa del índice de Kappa utilizada clásicamente en la que la fuerza de concordancia se califica como:

• pobre o débil para valores menores a 0,40,

•moderada, para valores de entre 0,41 y 0,60,

• buena, entre 0,61 y 0,80, y

• muy buena para valores superiores hasta 1.¹³

Es importante resaltar que estos rangos son amplios y arbitrarios, lo que implica por ejemplo que moverse de un valor del 60 al 61%, significaría pasar de una concordancia moderada a una buena. Tales rangos no consideran las características propias de cada uno de los fenómenos que se intentan medir ni la relevancia clínica que, en un momento dado, puedan adquirir las diferencias o similitudes encontradas, que son dependientes de la entidad o el fenómeno a medir. Esto quiere decir que para algunos fenómenos, diferencias del 1% pueden ser clínicamente relevantes (por ejemplo la saturación de oxígeno arterial), mientras para otros sólo diferencias mayores de 20% pueden tener implicaciones clínicas (ej. el peso fetal estimado por ultrasonido). Por lo tanto, sería conveniente la construcción de tablas de acuerdo que dependerían de consensos clínicos en torno a cada entidad nosológica o fenómeno a medir en particular.

Cuando se trata de variables nominales con más de una categoría, es necesario ajustar el índice de Kappa según el grado de discordancia entre las diferentes categorías, ya que no sólo se debe tener en cuenta la concordancia perfecta ocurrida entre los métodos u observadores para una misma categoría, sino las diferencias de clasificación ocurridas entre los observadores o los métodos para cada una de las categorías existentes y con un ajuste por el grado de discordancia en cada una de ellas. Este método se conoce como el índice de Kappa ponderado.¹⁴

Concordancia para variables de tipo contínuo

Cuando el fenómeno objeto de análisis es medido como una variable numérica continua, se han utilizado aproximaciones tales como el coeficiente de Pearson, el coeficiente de correlación intraclase (CCI) y el coeficiente de Lin.

El coeficiente de Pearson mide la probabilidad de establecer una ecuación lineal entre dos variables, en la que por cada cambio de unidad en una de ellas se espera un cambio de unidad (correlativo) en la otra, sin tener en cuenta ni la magnitud ni la escala de medición de las variables comprometidas. Su uso no es adecuado para estimar la concordancia entre dos variables dado que se pueden obtener coeficientes de correlación de Pearson muy cercanos a la unidad, como el encontrado por Faustin y colaboradores¹⁵ (de 0,94), aún entre fenómenos totalmente diferentes tales como la altura uterina medida en centímetros y la edad gestacional calculada en semanas, sin que exista concordancia entre ellas. Además, el rango de valores observado en la muestra incrementa el coeficiente de Pearson si ésta incluye valores extremos, sobreestimando la correlación obtenida entre las variables.¹⁶ Así, el coeficiente de Pearson mide la intensidad de la asociación lineal entre dos mediciones (correlación) pero no proporciona información acerca del acuerdo observado, ni sobre la presencia de diferencias sistemáticas entre las mediciones o instrumentos.

El coeficiente de correlación intraclase (CCI), introducido originalmente por Fisher, es una formulación especial del coeficiente de correlación (ρ) de Pearson. Este método permite evaluar la concordancia general entre dos o más métodos de medida u observación basado en un modelo de análisis de varianza (AnOVA) con medidas repetidas.¹⁷

Se define como la proporción de la variabilidad total que es debida a la variabilidad de los sujetos. Supone que la variabilidad total de las mediciones puede desagregarse en dos componentes: a) la variabilidad debida a las diferencias entre los sujetos (entresujetos) y b) la debida a la medición para cada sujeto (intrasujetos), la que a su vez se subdivide en: i) variabilidad entre observaciones y ii) variabilidad residual, debida al error que conlleva dicha medición. Este coeficiente estima el promedio de las correlaciones entre todas las posibles ordenaciones de los pares de observaciones disponibles, evitando así el problema de la dependencia del orden del coeficiente de correlación de Pearson. El CCI no explica o discrimina la variabilidad entre los métodos de medición o la debida a las diferencias entre observadores. Puede utilizarse cuando hay más de dos observaciones por sujeto. Dado que el CCI es una proporción, sus valores oscilan entre 0 y 1, y por tanto la máxima concordancia posible se alcanzaría cuando el CCI=1. Al igual que para el coeficiente de Kappa, su interpretación es bastante subjetiva y se han presentado diferentes tablas para su interpretación, entre ellas las de Fleiss¹⁸ y las de Prieto y Lamarca.¹⁹ En general, se considera que valores por debajo de 0,4 indican baja fiabilidad; cuando se encuentran entre 0,4 y 0,75 una fiabilidad entre regular y buena; y valores superiores a 0,75 se refieren a una fiabilidad excelente.

Por ejemplo, este instrumento se utiliza en un estudio publicado por Kruger y colaboradores,²⁰ en el que se comparan las mediciones de la función del piso pélvico usando ultrasonido 3D y la resonancia magnética nuclear en mujeres nulíparas. Ellos encontraron un CCI entre 0,58 y 0,78, con el cual consideraron que existe una reproducibilidad de moderada a buena entre los métodos, siendo menor para la medición del área axial del hiato urogenital durante la maniobra de Valsalva y buena para la medición de esta misma área en reposo.

Aunque este coeficiente ha sido muy usado para medir concordancia, tampoco es un método ideal pues tiene varios supuestos difíciles de cumplir: a) que los métodos evaluados provienen de una muestra al azar de una población de métodos, b) que el error de medición es similar para cada uno de los métodos,¹⁷ y c) al igual que el coeficiente de Pearson, depende de los valores en estudio. Por ejemplo, si la variabilidad entre estos es muy poca el CCI va a ser bajo, independientemente de que los métodos sean o no concordantes y a mayor variabilidad entre los sujetos, mayor va a ser el CCI, lo que también significa que al depender de la variabilidad de los valores observados, su valor será mayor en muestras heterogéneas. Una desventaja adicional se relaciona con la dificultad para interpretar sus valores y su traducción a la relevancia desde el punto de vista clínico, tal como sucede con el coeficiente Kappa.

El uso del CCI se ha extendido en el contexto de valorar la reproducibilidad de varias mediciones o cuando se comparan dos métodos que tienen diferente unidad de medición, pero dentro del marco de la evaluación de la concordancia, tiene obvias desventajas. Cuando los datos no tienen una distribución normal, se puede acudir al uso de pruebas no paramétricas como la prueba Tau de Kendall.²¹

De otro lado, y para superar las limitaciones de las pruebas estadísticas antes descritas, Lin (1989)²² desarrolló una propuesta para evaluar la concordancia entre variables continuas a través del coeficiente de correlación concordancia (CCC).

El CCC sigue la ecuación:

Donde: A² = Varianza del método A

B² = Varianza del método B

C² = Varianza de la diferencia entre los métodos A y B

D² = Diferencia promedio de los dos métodos.

Este coeficiente califica la fuerza del acuerdo de una forma más exigente: para variables continuas, la valora como casi perfecta para valores mayores a 0,99; sustancial, de 0,95 a 0,99; moderada, de 0,90 a 0,95 y pobre cuando está por debajo de 0,90. Para variables categóricas, los valores sugeridos son: mayor a 0,90, entre 0,80 y 0,90, de 0,65 a 0,80 y menor de 0,65, respectivamente.

El CCC, definido también por la fórmula CCC=ρCb, combina una medida de precisión, representada por el coeficiente de correlación (ρ), con una medida de exactitud, representada por el coeficiente de corrección de sesgo (Cb). Permite observar qué tan lejos se desvían los datos observados por dos métodos u observadores de una línea a partir del origen y a 45° en un plano cartesiano, que corresponde a la línea de perfecta concordancia. Este coeficiente aumenta de valor en función de: a) la cercanía del eje principal o la pendiente de la curva de regresión de las parejas de datos obtenidos en la línea de perfecta concordancia (coeficiente de corrección de sesgo) que permite evaluar la exactitud de los datos obtenidos y b) en función de la dispersión alrededor de la línea de mejor ajuste o línea de regresión de las parejas de los datos obtenidos, siendo éste el reflejo de la precisión de las mediciones obtenidas y corresponde al coeficiente de correlación de Pearson.²³ El CCC adquiere valores entre -1 (perfecta discordancia) a +1 (concordancia perfecta). En caso de un acuerdo perfecto en términos de precisión y exactitud, el CCC corresponde a un valor de +1. Lo anterior significa que cuando todos los datos obtenidos por ambos métodos caen sobre la línea de concordancia, habrá reproducibilidad perfecta.²⁴ El resultado arrojado es por tanto, el grado de reproducibilidad, como lo refiere Lin.²⁵

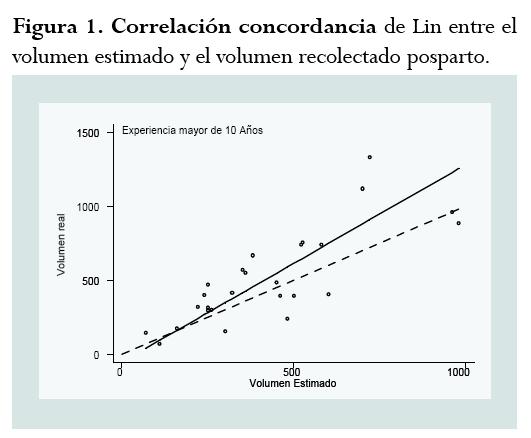
En un estudio realizado por Rubio y sus colegas para evaluar la concordancia entre la estimación visual y la recolección sistemática del sangrado posparto, se obtuvo un CCC de 0,73, cuando los evaluadores del sangrado fueron personas con más de 10 años de experiencia.²⁶ El coeficiente obtenido está discriminado de la siguiente forma: coeficiente de Pearson (ρ)=0,80 y coeficiente de corrección de sesgo (exactitud) (Cb)=0,91. Este resultado demuestra una pobre concordancia o grado de acuerdo según los valores propuestos por Lin para variables continuas. La figura 1 permite mostrar el análisis del CCC obtenido de acuerdo con la descripción realizada.

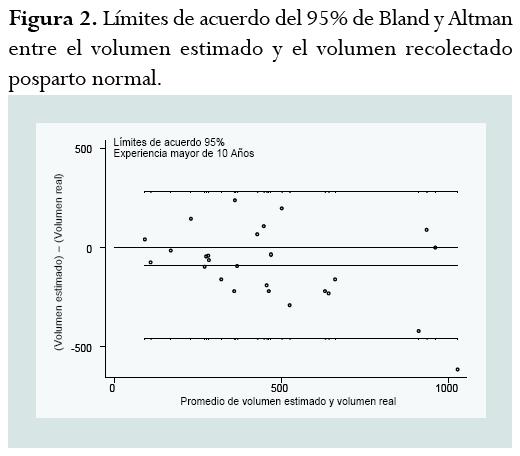
El CCC también proporciona los datos para establecer los límites de acuerdo desarrollados por Bland y Altman, que son una aproximación complementaria al CCC de Lin.²⁷ Este método gráfico se basa en el análisis de las diferencias entre las mediciones individuales por cada método o de cada medición²⁸ y representa en forma gráfica las diferencias entre dos mediciones del mismo sujeto o fenómeno en el eje de las ordenadas (y) frente a la media obtenida de ambas mediciones en el eje de las abscisas (x). Esto permite conocer si las diferencias entre los dos métodos son sistemáticas o, al contrario, debidas al azar. Se espera que la diferencia promedio entre dos métodos sea de “0” y que el 95% de las diferencias se encuentren dentro de 1,96 de las desviaciones estándar de dicho promedio. Si estas diferencias no son clínica o biológicamente importantes, los dos métodos pueden considerarse como concordantes e intercambiables. A partir de la desviación estándar de las diferencias entre los métodos también es posible calcular los intervalos de confianza para los límites de concordancia, siempre y cuando tales diferencias se distribuyan normalmente y que la diferencia de los dos métodos sea independiente de la magnitud del valor de la característica medida. Dados los requisitos de normalidad que exige la distribución de los datos cuando se emplea el CCC, debe procurarse que tales supuestos se cumplan, aunque se ha demostrado que el CCC de Lin es robusto y no se modifica de manera significativa cuando no se cumplen los supuestos de normalidad.

La figura 2 permite ejemplificar el uso del análisis gráfico de Bland y Altman al evaluar la concordancia entre la estimación visual y la estimación real del sangrado posparto normal, por personal calificado con más de 10 años de experiencia.²⁶ Aquí se observa que la diferencia promedio entre los métodos es de -90 ml, que corresponde a una subestimación del volumen de sangrado calculado respecto al volumen real. Los límites de acuerdo del 95% en este caso tienen una gran variabilidad (casi 800 ml) y la pertinencia o relevancia clínica de este hallazgo es dependiente del fenómeno estudiado y sus características. Así las cosas, una diferencia en la estimación de un sangrado de 100 ml no tiene la misma relevancia clínica que una diferencia de un (1) cm² en el área de una válvula cardíaca o de una comunicación interventricular.

Adicionalmente, el coeficiente de correlación concordancia (CCC) también puede ser usado para validar la reproducibilidad de un instrumento o método, ya que permite evaluar el acuerdo entre muestras pareadas.

Existe una dificultad para la interpretación de los coeficientes que miden la concordancia que surge desde la definición de la hipótesis nula para estos estudios. La hipótesis nula habitual de la concordancia = 0 vs. concordancia ≠ 0, no tiene sentido ya que en el caso de rechazar la hipótesis nula se concluiría que la concordancia no es cero, es decir que los datos no son independientes (ya que miden el mismo fenómeno) y lo que es lo mismo, que la discordancia no es total. Si no se rechaza la hipótesis nula, debería sospecharse bien de falta de poder (tamaño muestral pequeño) o de errores en la medición. Por tanto, es más adecuado plantear el contraste de la hipótesis a una sola cola, estableciendo el valor mínimo de la concordancia, es decir del CCC, que se desea evaluar o se considera el mínimo aceptable entre los métodos. Aquí el problema aparece en la fijación de dicho límite, pues se basa en un criterio subjetivo propio para cada instrumento o fenómeno a medir. Bajo esa perspectiva y teniendo en cuenta que no siempre ni para todos los casos hay un consenso acerca de qué valores deberían considerarse como criterio de concordancia, deberá asumirse en cada caso el más aceptado en la comunidad científica o aquel más próximo a la referencia teórica existente.

Lo anterior significa e implica, que, en ocasiones, interesa más conocer el grado de concordancia que poner a prueba la hipótesis nula de discordancia total y en este sentido, hay que tomar una posición y asumir desde el punto de vista clínico, un nivel esperado como “aceptable” a partir del cual los clínicos consideren que los métodos o instrumentos reportan la misma información fiable y repetible y por lo tanto, se pueden utilizar indistintamente para la toma de decisiones para el manejo clínico de los pacientes a nuestro cuidado.

Los métodos estadísticos para la evaluación de la concordancia y la reproducibilidad son dependientes de las características del fenómeno clínico a estudiar y deben estar sujetos a una metodología rigurosa y específica. Su selección depende del tipo de variable a medir y de los parámetros que se quieran evaluar, si sólo reproducibilidad o también exactitud.

1. Gaitán-Duarte H, Rubio-Romero J, Gómez-Chantraine M. Interpretación del desempeño operativo de las pruebas de tamizaje y de diagnóstico de enfermedades en obstetricia y ginecología. Rev Colomb Obstet Ginecol 2009;60:365-76.         [ Links ]

2. Alcázar JL, Mercé LT, Manero MG, Bau S, López-García G. Endometrial volume and vascularity measurements by transvaginal 3-dimensional ultrasonography and power Doppler angiography in stimulated and tumoral endometria: an interobserver reproducibility study. J Ultrasound Med 2005;24:1091-8.         [ Links ]

3. Monsonego J, Pollini G, Evrard MJ, Sednaoui P, Monfort L, Zerat L, et al. Detection of human papillomavirus genotypes among high-risk women: a comparison of hybrid capture and linear array tests. Sex Transm Dis 2008;35:521-7.        [ Links ]

4. Didacterion, Diccionario latín-español. [Sitio en Internet]. Visitado 2010 Mar 8. Disponible en: http://recursos.cnice.mec.es/latingriego/Palladium/5_aps/diclat.php        [ Links ]

5. Cortés-Reyes, E. Comparación en la estimación del VO_2max a través de un monitor de frecuencia cardíaca Polar S810 y una prueba de esfuerzo maximal en banda sin fin según el protocolo de Balke, en deportistas universitarios entrenados en resistencia aeróbica en la ciudad de Bogotá, D.C. Tesis de Maestría en Epidemiología Clínica, Universidad nacional de Colombia; 2008         [ Links ]

6. Kramer MS, Feinstein AR. Clinical biostatistics. LIV. The biostatistics of concordance. Clin Pharmacol Ther 198129:111-23.        [ Links ]

7. Fernández P, Díaz P. La fiabilidad de las mediciones clínicas: el análisis de concordancia para variables numéricas. [Sitio en Internet]. Visitado 2010 Jul 6. Disponible en: http://www.fisterra.com/mbe/investiga/conc_numerica/conc_numerica.pdf         [ Links ]

8. Cortés-Reyes E, Echeverry-Raad J, Mancera-Soto E, Ramos-Caballero D. Concordancia en la estimación del consumo máximo de oxígeno entre una prueba de esfuerzo y el Polar S810. Rev salud pública 2009;11:819-27.        [ Links ]

9. van Randen A, Laméris W, Nio CY, Spijkerboer AM, Meier MA, Tutein Nolthenius C, et al. Inter-observer agreement for abdominal CT in unselected patients with acute abdominal pain. Eur Radiol 2009;19:1394-407.        [ Links ]

10. Cepeda M, Perez A. En: Ruiz M, Gómez C, Londoño D. Investigación Clínica: Epidemiología clínica aplicada. Centro Editorial Javeriano; 2001. p. 288-301.         [ Links ]

11. Massad LS, Jeronimo J, Schiffman M; National Institutes of Health/American Society for Colposcopy and Cervical Pathology (nIH/ASCCP) Research Group. Interobserver agreement in the assessment of components of colposcopic grading. Obstet Gynecol 2008;111:1279-84.        [ Links ]

12. Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics 1977;33:159-74.        [ Links ]

13. Altman DG. Practical statistics for medical research. new York: Chapman and Hall/CRC; 1991. p. 277-300.        [ Links ]

14. Cohen J. Weighted kappa: nominal scale agreement with provision for scaled disagreement or partial credit. Psychol Bull 1968;70:213-20.        [ Links ]

15. Faustin D, Gutiérrez L, Gintautas J, Calame RJ. Clinical assessment of gestational age: a comparison of two methods. J natl Med Assoc 1991;83:425-9.        [ Links ]

16. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986;1:307-10.        [ Links ]

17. Bland JM, Altman DG. A note on the used of the intraclass correlation in the evaluation of agreement betwen two methods of measurement. Comput Biol Med 1990;20:337-40.        [ Links ]

18. Fleiss JL. The design and analysis of clinical experiments. new York: Wiley; 1986.        [ Links ]

19. Prieto L, Lamarca R, Casado A. Assessment of the reliability of clinical findings: the intraclass correlation coefficient. Med Clin (Barc) 1998;110:142-5.        [ Links ]

20. Kruger JA, Heap SW, Murphy BA, Dietz HP. Pelvic floor function in nulliparous women using threedimensional ultrasound and magnetic resonance imaging. Obstet Gynecol 2008;111:631-8.        [ Links ]

21. Coeficiente de correlación simple por rangos de Kendall [Sitio en Internet] Visitado 2010 Jun 25. Disponible en: http://www.ray-design.com.mx/psicoparaest/index.php?option=com_content&view=article&id=254:coeficiente-kendall1&catid=54:coeficientecorrela&Itemid=75        [ Links ]

22. Lin L. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989;45:255-68.        [ Links ]

23. Cepeda MS, Africano JM, Polo R, Alcalá R, Carr D. Agreement between percentage pain reductions calculated from numeric rating scores of pain intensity and those reported by patients with acute or cancer pain. Pain 2003;106:439-42.         [ Links ]

24. Zar JH. Biostatistical Analisis. Third edition. Upper Saddle River, NJ, USA: Prentice-Hall, Inc.; 1996.         [ Links ]

25. NIWA, National Institute of Water & Atmospheric Research. Taihoro nukurangi. [Sitio en Internet]. Visitado 2010 Jul 6. Disponible en: http://www.niwascience.co.nz/services/free/statistical/concordance.         [ Links ]

26. Rubio-Romero JA, Gaitán-Duarte HG, Rodríguez-Malagón N. Concordancia entre la estimación visual y la medición del volumen recolectado en un bolsa del sangrado intraparto en mujeres con parto normal en Bogotá, Colombia, 2006. Rev Colomb Obstet Ginecol 2008;59:92-102.        [ Links ]

27. Carrasco JL, Jover L, King TS, Chinchilli VM. Comparison of concordance correlation coefficient estimating approaches with skewed data. J Biopharm Stat 2007;17:673-84.         [ Links ]

28. Bland JM, Altman DG. Measurements error and correlation coefficients. BMJ 1996;313:41-2.         [ Links ]

Conflicto de intereses: ninguno declarado.