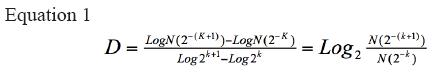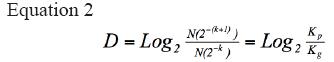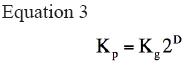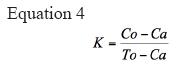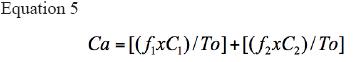Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de la Facultad de Medicina
Print version ISSN 0120-0011
rev.fac.med. vol.62 no.4 Bogotá Oct./Dec. 2014
https://doi.org/10.15446/revfacmed.v62n4.43444
DOI: http://dx.doi.org/10.15446/revfacmed.v62n4.43444
ORIGINAL RESEARCH
Application of the chaotic power law to the study of cardiac dynamics in patients with arrhythmias
Aplicación de la ley exponencial caótica al estudio de la dinámica cardíaca de pacientes con arritmias
Javier Rodríguez-Velásquez1,2,3, Signed Prieto1,3, Darío Domínguez4 , Catalina Correa1,3 , Martha Melo4, Juan Pardo5, Fernán Mendoza6, Ligia Victoria Rodríguez1,3 , Diana Margarita Cardona1,3, Laura Méndez2
1 Grupo Insight, Universidad Militar Nueva Granada. Bogotá, Colombia.
2 Línea de Profundización e Internado Especial Física y Matemáticas Aplicadas a la Medicina, Universidad Militar Nueva Granada. Bogotá, Colombia.
3 Centro de Investigaciones Clínica del Country. Bogotá, Colombia.
4 Grupo de Investigación FRACUMNG. Facultad de Ciencias Básicas y Aplicadas-Universidad Militar Nueva Granada. Bogotá, Colombia.
5 Hospital Universitario Mayor Mederi. Bogotá, Colombia.
6 Programa de Cardiología, Fundación Clínica Abood Shaio. Bogotá, Colombia.
Correspondence: Javier Rodríguez-Velásquez. Carrera 79 B No. 51-16 sur, interior 5, apartamento 102. Bogotá, Colombia. Telephone: +57 1 4 52 22 57. E-mail: grupoinsight2025@yahoo.es.
Received: 13/05/2014 Accepted: 09/09/2014
Summary
Background. An exponential law for chaotic cardiac dynamics, found previously, allows the quantification of the differences between normal cardiac dynamics and those with acute diseases, as well as the cardiac dynamics of the evolution between these states.
Objective. To confirm the clinical applicability of the developed methodology through the mathematical law for cardiac dynamics in dynamics with arrhythmias.
Materials and methods. 60 Holter electrocardiograms were analyzed, 10 corresponded to normal subjects, and 50 to subjects with different arrhythmias. For each Holter, an attractor was performed, and its fractal dimension and spatial occupancy were measured. A mathematical evaluation was applied in order to differentiate normal dynamics from pathological ones. Sensitivity, specificity and the Kappa coefficient were calculated.
Results. The mathematical evaluation differentiated occupation spaces, normal dynamics, acute illness dynamics, and evolution between these states. The sensitivity and specificity values were 100%, and the Kappa coefficient was 1.
Conclusions. The clinical applicability of the methodology for cases with arrhythmia was shown. It is also applicable for the detection of changes in dynamics that are not classified clinically as pathological.
Keywords: Fractals; Nonlinear Dynamics; Diagnosis; Arrhythmias, Cardiac; (MeSH).
Rodríguez-Velásquez J, Prieto S, Domínguez D, Correa C, Melo M, Pardo J, et al. Application of the chaotic power law to cardiac dynamics in patients with arrhythmias. Rev Fac Med. 2014;62(4):539-46. http://dx.doi.org/10.15446/revfacmed.v62n4.43444.
Resumen
Antecedentes. Se ha encontrado una ley exponencial para los sistemas dinámicos caóticos cardíacos que logra cuantificar las diferencias entre dinámicas cardíacas normales y aquellas con enfermedad aguda, así como la evolución entre estos estados.
Objetivo. Confirmar la aplicabilidad clínica de la metodología desarrollada a partir de la ley matemática para la dinámica cardiaca en dinámicas con arritmia.
Materiales y métodos. Se analizaron 60 holter, 10 correspondían a sujetos normales y 50 con diferentes tipos de arritmias. Para cada holter se construyó un atractor, se midió su dimensión fractal y ocupación espacial. Se aplicó la evaluación matemática para diferenciar dinámicas cardíacas normales de enfermas y en proceso de evolución. Se calculó la sensibilidad, especificidad y coeficiente Kappa.
Resultados. La evaluación matemática diferenció los espacios de ocupación, normalidad, enfermedad aguda y evolución entre estos estados. Los valores de sensibilidad y especificidad fueron de 100% y el coeficiente Kappa fue de 1.
Conclusiones. Se evidenció la aplicabilidad clínica de la metodología para casos con arritmias, siendo capaz de detectar cambios en la dinámica que no son clasificados como patológicos clínicamente.
Palabras clave: Fractales; Dinámicas no Lineales; Diagnóstico; Arritmias Cardíacas (DeCS).
Rodríguez-Velásquez J, Prieto S, Domínguez D, Correa C, Melo M, Pardo J, et al. Aplicación de la ley exponencial caótica al estudio de la dinámica cardiaca de pacientes con arritmias. Rev Fac Med. 2014;62(4):539-46. http://dx.doi.org/10.15446/revfacmed.v62n4.43444.
Introduction
From the temporary changes of the dynamic variables of a system, it is possible to determine its behavior. Predicting this behavior is the central problem of dynamical systems (1,2). In this theory, dynamical variables that are called attractors are put into graphic representations in the phase space (3). If they are completely irregular, they are chaotic attractors that can be studied with fractal geometry. Fractal geometry studies irregular objects of nature (4-6) rather than regular geometric objects that are studied by Euclidean geometry.
There are several types of fractals. One of them, called the wild fractals, involves the super-positioning of its parts. To calculate its degree of irregularity —the fractal dimension— the box-counting method is generally used (7). This method allows us to observe the spatial distribution of a particular object in different scales through the use of overlapping grids of different sizes.
According to the World Health Organization, cardiovascular diseases (CVD) represent 1.9% of yearly deaths in the Americas. CVDs are known as non-communicable diseases. Among these are included myocardial infarction and stroke. It is estimated that one in four people suffer from this disease category and that, by 2030, approximately 23.6 million people could die from this condition (8). One of the CVDs with the greatest incidence is arrhythmia (9), being associated with 50% of CVD deaths. According to medical literature, they can be divided into three categories: passive arrhythmias, automatic or ectopic arrhythmias, and re-entry arrhythmias (10).
The most important diagnostic test for identifying significant —but of transitory, sudden, asymptomatic presentation— alterations in cardiac rhythm is the Holter test (11). This test allows for the visualization of the RR interval, with which interpretations regarding the variability of the heart rate (12), the appearance of non-mortal post-infarction arrhythmic events (13), and arrhythmias as a means of cardiovascular deterioration in the context of sepsis (14) can be made.
A new interpretation of the concept of normality-disease has developed from the dynamical systems theory. In this new interpretation, an unhealthy dynamic would be either very regular or highly random (15-19) and a normal dynamic would be placed in between these two extremes. From this conception, measurements that seek to obtain better analyses of cardiac dynamics have been developed (20-23). However, it is still debatable which of these methods should be applied and under which conditions (24). In some cases, more than one study may be required to ascertain their applicability (25).
The opportune diagnosis and treatment of arrhythmic cardiac conditions are of much relevance given their association with acute illnesses (26,26). The establishment of a measurement that allows for the quantification of the differences between arrhythmias that evolve into acute illnesses and arrhythmias that do not evolve into acute illnesses could help us to understand what type of intervention would be most appropriate. It could also help to give some patients priority care (28). New methodologies (29,30) have been developed from mathematical laws and theories that have allowed us to make objective quantifications and predictions regarding cardiac dynamics.
An example of this is a methodology for the mathematical evaluation of the Holter test for which a power law (30) for chaotic cardiac dynamics was found. In this study, through the quantification of the occupancy space of attractors generated from the Holter values of the heart rates, normality was differentiated from acute illness and the evolution between these states.
Based on the evaluation method found previously (30), this investigation sought to analyze cardiac dynamics associated with arrhythmias in order to test its evaluation capacity and its clinical applicability and as a diagnostic aid.
Materials and methods
Definitions
Heart rate map delay: a diagram in which each heart rate is plotted as a function of the previous heart rate.
Box-counting of fractal dimensions (D) (7):
N(2-k) is a function of the degree of partitions of the grid k. It corresponds to the number of boxes occupied by the object in the grid with partitions 2-k.
Power law of the chaotic cardiac dynamic: by renaming the values of the function N(2-k) as Kp for the grid with the smallest partitions, and Kg for the grid with the biggest partitions, equation 1 takes on the following form (30):
By solving for Kp, an exponential relationship between the occupied spaces and the fractal dimension (D) (30) is obtained:
Population
A total of 60 Holter electrocardiograms of at least 21 hours were taken. Of these, 10 corresponded to cases diagnosed as normal by an expert cardiologist. The other 50 cases corresponded to cases diagnosed with different types of arrhythmias suffered by individuals with more than 21 years of age. All of the electrocardiograms were taken with the same brand of Holter monitor, and are therefore standardized.
Procedure
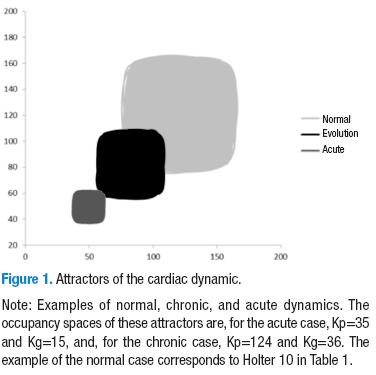
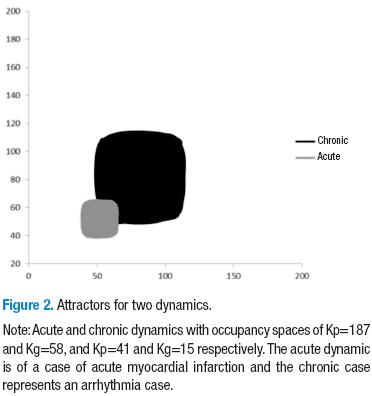
The maximum and minimum values of the heart rates, along with the total number of beats per hour, were taken for the analysis of the electrocardiographic records. Later, these values were processed by a previously developed program (30) that generates a sequence of the heart rates obtained through the Holter test by using an equiprobable algorithm. After, the sequences were plotted in the phase space through the use of a delay map (see definitions), making in this way the chaotic attractor of the cardiac dynamics (Figures 1 and 2).
Later, we proceeded to calculate the fractal dimension with the Box-counting method (Equation 1), overlaying two grids in order to quantify the spaces occupied by each attractor. The physical and mathematical evaluation of each of the Holter electrocardiograms was established according to the previously developed methodology (30). In this way, a Holter electrocardiogram is associated with the physical-mathematical characteristics of acute disease when the Kp occupancy spaces of their chaotic attractors are inferior to 73. A physical-mathematical diagnosis of normality will be established when Kp occupancy spaces with values greater than 200 are found. A state of evolution toward disease would be considered when occupancy spaces have a value of between 73 and 200. Later, we looked for consistencies or divergences when we compared the physical-mathematical diagnosis to the conventional diagnosis.
Statistical analysis
The clinical confirmation of the results found upon applying this methodology was compared to the conventional clinical diagnosis, as a gold standard test. These measurements were made with a binary classification, in which true positives (TP) represent cases evaluated conventionally and mathematically as being pathological; false positives (FP) represent cases that were diagnosed conventionally by an expert as being normal, but that mathematically had disease values; false negatives (FN) represent cases that were evaluated mathematically as within the normal limits, but that had a conventional diagnosis of disease; and, lastly, true negatives (TN) represent cases that were diagnosed both mathematically and conventionally as normal. Finally, we proceeded to evaluate the consistency between the conventional and physical-mathematical diagnoses through the Kappa coefficient equation (31):
Where Co represents the number of consistencies observed, corresponding to the number of patients with the same diagnoses from both the mathematical methodology and the gold standard. To represents the totality of cases. Ca corresponds to the number of consistencies attributable to chance, calculated through the following equation (31):
Where f1 is equal to the number of cases with mathematical values of normality, C1 represents the number of cases diagnosed as normal by the clinical expert, f2 equals the number of cases mathematically evaluated as being of disease, C2 equals the number of cases diagnosed as having a pathology in the clinical environment, and To refers to the total number of cases.
Ethical aspects
This study is declared to be a minimum risk investigation in accordance with Resolution 8430 of 1993 of the Colombian Ministry of Health, since it involves physical and mathematical calculations on exam reports, and non-invasive paraclinical procedures that have been previously prescribed according to conventionally established protocols. The anonymity and integrity of the participants was also protected. The study complied with the ethical principles of the Helsinki Declaration from the World Medical Association.
Results
The values of the fractal dimensions of the attractors corresponding to each cardiac dynamic were between 0.7464 and 1.9875. The spaces occupied by the Kp grid were between 30 and 336, with the Kg values were between 8 and 183. The dynamics that were mathematically evaluated as acute, with spatial occupancy values of between 33 and 68 in Kp grid were 14. Dynamics evaluated as cases that were evolving towards disease amounted to 36, with occupancy values on the Kp grid of between 99 and 197 (Table 1). All Holter cardiograms classified as normal showed Kp occupancy values of more than 200, which corresponds to a mathematical evaluation of normality (Table 1).
Sensitivity and specificity values of 100% were found, along with a Kappa coefficient of 1. The methodology differentiates adequately the cases of normality, cases of acute pathologies, and cases that are evolving toward a case of acute arrhythmia. For the Holters that were clinically classified as within normal limits, but that presented alterations in the heart rhythm, the spatial occupancy was between 38 and 65 for the Kg grid, and between 115 and 197 for the Kp grid (Table 1). This corresponds to a mathematical assessment of evolution, which shows the capability of the mathematical methodology to evaluate slight changes in the cardiac dynamic that are not taken into account in clinical conclusions.
By comparing the occupancy spaces between normal attractors, in evolution attractors, and acute disease attractors, it was possible to observe the reduction in the size of the attractor in the phase spaces (Figures 1 and 2) as the dynamic evolves toward an acute state. As could be observed in Figures 1 and 2, the attractors corresponding to an acute dynamic occupy less space than those corresponding to chronic or normal dynamics. It can be seen that their heart rates are in a narrower range than the range in which the heart rates of chronic and normal dynamics are found. This could correspond to the difference in spatial occupancy of the different dynamics.
Discussion
This is the first study in which a mathematical law of chaotic cardiac dynamics has been applied to the analysis and assessment of 60 Holter records with normal and arrhythmic dynamics. By quantifying the occupancy spaces to the attractors of the dynamics, objective and reproducible differences between the studied dynamics were found. The quantification of the arrhythmic dynamics also let us observe that the methodology is able to quantitatively evaluate the degree of abnormality in the cardiac dynamic in such a way that the dynamics classified clinically as being within the bounds of normality were evaluated as being in evolution toward disease by the mathematical methodology. This shows the capacity of the methodology for quantifying changes in the dynamic that were omitted by the conventional clinical classification. This makes the methodology a useful diagnostic aid in clinical practice.
In a previous study (30) with the power law of chaotic cardiac dynamics it was possible to deduce all of the possible cardiac attractors by their spatial occupancy values in the box-counting space. In accordance with this spatial distribution, normal cardiac dynamics were differentiated from those related to acute pathological states, while those that were in intermediate values between these first two states corresponded to cases of evolution toward disease or normality.
Fractal geometry has been applied in different fields of medicine to differentiate normality from a disease state (32-35). However, isolated fractal dimensions have proven non-conclusive for achieving this differentiation (36-37). For this reason, different concepts have been developed in search of this differentiation (38,39). In the same way, isolated fractal dimensions have been shown to be insufficient for differentiating normality and disease in cardiac dynamics, something that has been evidenced by the application of the mathematical law (30, 41, 42). In this way, the occupancy spaces of the attractor allow us to establish a differential diagnosis for each particular case, independently of the statistical and epidemiological methodologies that describe population behaviors.
Analyzing physiological dynamics through linear methods, the chaos theory, and fractal analysis has contributed to the development of new methodologies for its study (17-23). From here, important considerations have been made, including a new conception of normality and disease (15), as well as better predictors of mortality and new indexes for quantifying the complexity of the dynamics studied. Nevertheless, it is necessary to perform more studies to ascertain their clinical applicability (24,25).
The methodology was applied to cases with diagnoses of arrhythmia, finding that all possible variants of arrhythmias can be evaluated quantitatively with the methodology. This shows the degree of evolution toward acute disease, meaning that the methodology is also capable of showing slight changes in the cardiac dynamic that are not classified clinically as pathological. The maximum level of consistency (Kappa coefficient) between the physical-mathematical diagnosis and the gold standard was obtained. Furthermore, the sensitivity and specificity was 100%. This shows that the methodology is capable of differentiating normal dynamics from dynamics with arrhythmias objectively and quantitatively.
Today, in clinical practice, methodologies based on statistical and population analyses that relate causes and effects have been applied generally without allow for affirmations about specific cases. This study leans on the method of theoretical physics in which, based on abstractions and inductions about the phenomenon that are observed with physical-mathematical theories and laws, the phenomenon is described to that point at which it is applicable to all cases and to any case in particular. Furthermore, it allows us to evaluate the phenomenon independently of the risk factors or statistical variables.
This methodology, thanks to its simplicity, could be implemented through software attached to the Holter devices or used in the analysis of the Holter data. This would allow for the automatic mathematical evaluation of the data, which would be an aid in daily clinical practice.
In other areas of medicine, generalizations have been obtained that allow for the prediction of a specific phenomenon, like the field of morphometry (38,39), infectology (43), and epidemiology (44). In the field of molecular biology and immunology, a theory was developed that enables the prediction of the phenomena involving the union of peptides to class 2 HLA based on entropy and probability (45). Elsewhere, applications have been found in the field of cardiology (46) for the intensive care unit (47,48).
Conclusions
The mathematical law of chaotic cardiac dynamics applied in this study to normal and arrhythmic dynamics allowed for the quantification in an objective and reproducible way of the occupancy spaces of the attractors. From this quantification, quantitative differences between the dynamics studied could be ascertained.
The application of the mathematical law for the particular study of cases with arrhythmia was able to assess different degrees of abnormality in the cardiac dynamics. This showed the capacity of the methodology to quantify changes in the dynamics that could be perceived in the conventional clinical classification. Thus, this methodology represents a useful tool for aiding diagnosis in clinical practice.
Conflict of interests
None declared by the authors.
Financing
Product of project CIAS-1455 financed by the Vice-Presidency of Research at the Universidad Militar Nueva Granada. 2014.
Acknowledgments
A special thank-you goes to all the directors of the Faculty of Basic and Applied Sciences and Medicine at the Universidad Militar Nueva Granada. The authors also thank the Clínica del Country Research Center for their support of this study. The authors also extend their thanks to Hospital Universitario Mayor Méderiand the Abood Shaio Clinical Foundation.
References
1. Devaney R. A first course in chaotic dynamical systems theory and experiments. Reading Mass: Addison-Wesley. 1992:10-50. [ Links ]
2. Peitgen H, Jürgens H, Saupe D. Strange attractors, the locus of chaos. En: Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag. 1992:185-226. [ Links ]
3. Calabrese JL. Ampliando las fronteras del reduccionismo. Deducción y sistemas no lineales. Psicoanálisis AP de BA. 1999;21:431-53. [ Links ]
4. Mandelbrot B. Cambios de escala y leyes potenciales sin geometría. In: The Fractal Geometry of Nature. San Francisco: Freeman Ed; 1972:477-87. [ Links ]
5. Mandelbrot B. Árboles jerárquicos o de clasificación, y la dimensión. In: Los Objetos Fractales. Barcelona: Tusquets Eds S.A. 2000:161-6. [ Links ]
6. Mandelbrot B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science. 1967;156:636-8. http://doi.org/cn376n. [ Links ]
7. Peitgen H, Jürgens H, Saupe D. The Box-Counting Dimension In: Chaos and Chaos and Fractals; New Frontiers of Science. New York: Springer-Verlag;1992:202-3. [ Links ]
8. OMS. Centro de prensa. Día mundial del corazón: Enfermedades Cardiovasculares causan 1,9 millones de muertes al año en las Américas [Internet]. Nota informativa octubre de 2012 [cited 2013 Feb 13] Available from: http://goo.gl/KOHHbI. [ Links ]
9. Gaziano T, Gaziano M. Global Burden of Cardiovascular Disease. En Braunwald's Heart Disease. Philadelphia: Elsevier Saunders; 2012. [ Links ]
10. Charria D, Sánchez C. Arritmias y trastornos de conducción. Oficina de recursos Educaconales-FEPAFEM. [Internet]. [cited 2014 Jan 13]. Available from: http://goo.gl/GeX70w. [ Links ]
11. Pineda M, Matiz H, Rozo R. Enfermedad coronaria. Bogotá: Editorial Kimpres Ltda; 2002. [ Links ]
12. Barron H, Viskin S. Autonomic markers and prediction of cardiac death after myocardial infarction. Lancet. 1998;351:461-2. http://doi.org/dbkbp4. [ Links ]
13. Kouchoukos N, Blackstone E, Hanley F, Kirklin J. Cardiac Surgery. Morphology, diagnostic criteria, natural history, techniques, results and indications. Philadelphia: Elsevier Health Science; 2012. [ Links ]
14. Gómez D, Enciso O, Peña T, Segura D, Nieto E. ECAIS study: inadvertent cardiovascular adverse events in sepsis. Med Intensiva. 2012;36:343-50. http://doi.org/fzn89s. [ Links ]
15. Goldberger A, Amaral L, Hausdorff JM, Ivanov P, Peng Ch, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. PNAS. 2002;99:2466-72. http://doi.org/b227vx. [ Links ]
16. Higgins JP. Nonlinear systems in medicine. Yale J Biol Med. 2002;75:247-60. [ Links ]
17. Costa M, Goldberger AL, Peng CK. Multiscale etropy analysis of complex physiologic time series. Phys Rev Lett. 2002;89:0681021-4. http://doi.org/dwvzzn. [ Links ]
18. Wu GQ, Arzeno NM, Shen LL, Tang DK, Zheng DA, Zhao NQ, et al. Chaotic signatures of heart rate variability and its power spectrum in health, aging and heart failure. PLoS ONE. 2009;4:e4323. http://doi.org/bn7g5n. [ Links ]
19. Braun C, Kowallik P, Freking A, Hadeler D, Kniffki K, Meesmann M. Demonstration of nonlinear components in heart rate variability of healthy persons. Am J Physiol. 1998;275:H1577-84. [ Links ]
20. Huikuri HV, Mäkikallio TH, Peng Ch, Goldberger A.L, Hintze U, Moller M. Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infartion. Circulation. 2000;101:47-53. http://doi.org/zcx. [ Links ]
21. Porta A, Guzzetti S, Montano N, Furlan R, Pagani M, Malliani A, et al. Entropy, entropy rate and pattern classification as tools to typify complexity in short heart period variability series. IEEE Trans. Biomed Eng. 2001;48:1282-91. http://doi.org/d95fn3. [ Links ]
22. Guzzetti S, Barroni E, Garbelli PE, Ceriani E, Della P, Montano N, et al. Symbolic dynamics of heart rate variability: a probe to investigate cardiac autonomic modulation. Circulation. 2005;112:465-470. http://doi.org/bht4fw. [ Links ]
23. Maestri R, Pinna GD, Accardo A, Allegrini P, Balocchi R, D´Addio R, et al. Nonlinear indices of heart rate variability in chronic heart failure patients: redundancy and comparative clinical value. J Cardiovasc Electrophysiol. 2007;18:425&-33. http://doi.org/c5w3nm. [ Links ]
24. Voss A, Schulz S, Schroeder R, Baumert M, Caminal P. Methods derived from nonlinear dynamics for analysing heart rate variability. Philos Trans A Math Phys Eng Sci. 2009;367:277-96. http://doi.org/bqwcdb. [ Links ]
25. Perkiömäki J, Mäkikallio TH, Huikuri HV. Fractal and Complexity Measures of Heart Rate Variability. Clin Exp Hypertens. 2005;27:149-58. [ Links ]
26. Olasveengen TM, Eftestol T, Gundersen K, Wik L, Sunde K. Acute ischemic heart disease alters ventricular fibrillation waveform characteristics in out-of hospital cardiac arrest. Resuscitation. 2009;80:412-7. http://doi.org/br5dbt. [ Links ]
27. Prieto S, Young P, Ceresetto JM, Bullorsky EO. Terapia anticoagulante en fibrilación auricular. Medicina. 2011;71:274-82. [ Links ]
28. Neumar RW, Otto CW, Link MS, Kronick SL, Shuster M, Callaway CW, et al. Part 8: Adult Advanced Cardiovascular Life Support: 2010 American Heart Association Guidelines for Cardiopulmonary Resuscitation and Emergency Cardiovascular Care. Circulation. 2010;122:S729-67. http://doi.org/cc5n34. [ Links ]
29. Rodríguez J, Álvarez L, Tapia D, López F, Cardona M, Mora J, et al. Evaluación de la dinámica cardiaca de pacientes con arritmia con base en la Teoría de la Probabilidad. Medicina (Bogotá). 2012;34:7-16. [ Links ]
30. Rodríguez J. Mathematical law of chaotic cardiac dynamic: Predictions of clinic application. J Med Med Sci. 2011;2:1050-59. [ Links ]
31. Cerda J, Villarroel del P. Evaluación de la concordancia inter-observador en investigación pediátrica: Coeficiente de Kappa. Rev Chil Pediatr. 2008;79:54-8. http://doi.org/d5w7vg. [ Links ]
32. Dey P, Rajesh L. Fractal dimension in endometrial carcinoma. Anal Quant Cytol Histol. 2004;26:113-6. [ Links ]
33. Garte S. Fractal properties of the human genome. J Theor Biol. 2004;230:251-60. http://doi.org/cshx49. [ Links ]
34. Kikuchi A, Kozuma S, Yasugi T, Taketani Y. Fractal analysis of the surface growth patterns in endometrioid endometrial adenocarcinoma. Gynecol Obstet Invest. 2004;58:61-7. http://doi.org/dmdk82. [ Links ]
35. Zatloukal Z. Granulometry and fractal dimensions. Ceska Slov Farm. 2003;52:244-7. [ Links ]
36. Gazit Y, Baish J.W, Safabaksh N. Fractal characteristics of tumour vascular architecture during tumour growth and regression. Microcirculation. 1997:395-402. [ Links ]
37. Lefebvre F, Benali H.A. Fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys. 1995;22:381-90. http://doi.org/cbpgdn. [ Links ]
38. Rodríguez J, Prieto S, Correa C, Bernal P, Puerta G, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics. 2010;10:1-6. http://doi.org/cxsjqr. [ Links ]
39. Rodríguez J, Prieto S, Correa C, Posso H, Bernal P, Puerta G, et al. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Una nueva Metodología de Aplicación Clínica. Rev. Fac. Med. 2010;18:173-81. [ Links ]
40. Rodríguez J. Teoría de unión al HLA clase II teorías de Probabilidad Combinatoria y Entropía aplicadas a secuencias peptídicas. Inmunología. 2008;27:151-66. http://doi.org/d8xrvm. [ Links ]
41. Rodríguez J, Correa C, Melo M, Domínguez, D, Prieto S, Cardona DM, et al. Chaotic cardiac law: Developing predictions of clinical application. J Med Med Sci. 2013;4:79-84. [ Links ]
42. Rodríguez J, Narváez R, Prieto S, Correa C, Bernal P, Aguirre G, et al. The mathematical law of chaotic dynamics applied to cardiac arrhythmias. J Med Med Sci. 2013;4:291-300. [ Links ]
43. Rodríguez J, Prieto S, Correa C, Pérez C, Mora J, Bravo J, et al. Predictions of CD4 lymphocytes' count in HIV patients from complete blood count. BMC Medical Physics. 2013;13:1-6. http://doi.org/zc2. [ Links ]
44. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Pública. 2010;27:211-8. http://doi.org/c8xdjf. [ Links ]
45. Rodríguez J. Teoría de unión al HLA clase II teorías de probabilidad combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología. 2008;27:151-66. http://doi.org/d8xrvm. [ Links ]
46. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardiacos: Predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Revista Colombiana de Cardiología. 2010;17:115-29. http://doi.org/f2tdg6. [ Links ]
47. Rodríguez J. Proportional Entropy of the cardiac dynamics in CCU patients. Proceedings of the 7th International Meeting Intensive Cardiac Care, Tel Aviv, Israel, 30 October-1 November 2011. Israel heart society, European society of cardiology, EBAC; 2011. [ Links ]
48. Rodríguez J. Proportional Entropy applied to the Clinic Prediction of Cardiac Dynamics. Innovations in Cardiovascular Interventions, Tel Aviv, Israel, 2-4 December 2012. ICI meeting; 2012. [ Links ]