Introducción
En la época de Leibniz, la relevancia de los tratamientos acerca de cuestiones metodológicas se observa en diversos frentes, que van desde el método cartesiano para la obtención de todos los conocimientos verdaderos de los que sea capaz la razón humana, hasta la revitalización de métodos clásicos de la matemática, como se puede ver en la geometría analítica, que reasume el análisis de los antiguos en combinación con el álgebra para aplicarlo precisamente a la geometría. Naturalmente, en el siglo de la "revolución científica" tampoco podemos dejar de lado las novedades en el modo de abordar la ciencia natural, en especial los métodos de Galileo y Newton (cf. Breger 160-162). Desde el punto de vista lógico, la cuestión en general no fue distinta. La revitalización de la distinción entre invención o descubrimiento y juicio de los estoicos llevada a cabo en el siglo anterior al de Leibniz por Petrus Ramus, bajo la modalidad de la distinción entre lógica de la invención y lógica del juicio, evidencia una preocupación metodológica significativa de la temprana modernidad, a saber, la de disponer no solo de un procedimiento que nos permita evaluar la corrección lógica de los conocimientos dispuestos, sino también de un mecanismo que nos permita obtener conocimientos nuevos (cf. Esquisabel 304). La intención de Francis Bacon en Novum Organum de reemplazar el órganon aristotélico por una lógica del descubrimiento es una muestra de ello (cf. Cellucci 157-160). No es de extrañar, entonces, que autores como Zabarella, quien por lo demás fue influyente en estas cuestiones metodológicas para el siglo XVII, hayan enfatizado específicamente el aspecto inventivo de los métodos, hasta el punto, de hecho, de definir el método en buena medida en virtud de ello, esto es, como "un hábito lógico o hábito intelectual instrumental que nos sirve para alcanzar la cognición de las cosas" (Zabarella T35).1
Ahora bien, en otros ámbitos del saber, la importancia de las cuestiones metodológicas no se limitó a un mero repensar o mejorar las técnicas ya conocidas. El desarrollo de la matemática infinita, por ejemplo, fue para la matemática del siglo XVI una nueva herramienta con la cual abordar, entre muchas otras cosas, algunos de los clásicos problemas de la geometría, como el de la cuadratura del círculo. Así, por ejemplo, para el tratamiento de problemas de cuadraturas en general, se desarrollaron diferentes variantes del método de los indivisibles, cuyo nombre es debido al célebre tratado de Bonaventura Cavalieri, Geometria indivisibilibus continuorum nova quadam rationepromota (cf. 1653), que, de alguna manera, fue el trabajo fundacional de la "tradición" de los métodos de los indivisibles. Naturalmente, todo esto trajo consigo nuevas exigencias metodológicas. Para las demostraciones en materia de cuadraturas, los matemáticos de la temprana modernidad reconocieron la rigurosidad del método de exhaución o de doble reducción al absurdo de Arquímedes. La importancia de Arquímedes para los matemáticos de este siglo, en especial para el tratamiento de problemas de cuadraturas, fue decisiva. Por esta razón, por ejemplo, Cavalieri señaló que sus argumentos por medio de indivisibles pueden reducirse ad stylum Archimedeum (cf. Cavalieri 1647 235; cf. Breger 163) y que en ocasiones evitó hacer uso de indivisibles, optando por demostrar stylo Archimedeo (cf. Cavalieri 1647 322; cf. Andersen 347-348). Por su parte, para Roberval la diferencia entre el método de los indivisibles y el método de exhaución es simplemente una diferencia en la manera de hablar (cf. Andersen 31). Wallis, por su lado, fue explícito al señalar que la Arithmetica infinitorum "también depende del método de exhauciones" (cf. Wallis prefacio). No obstante, hay que sumarle a todo esto, por un lado, como ya señalamos, la exigencia de desarrollar métodos no solo demostrativos, sino también heurísticos, y por otro, la intención, en ocasiones, de elaborar métodos generales, en el sentido de que permitan no solo descubrir nuevas verdades, sino también, al mismo tiempo, demostrar las verdades halladas.
Esta última cuestión la podemos observar con claridad, por ejemplo, en el tratado de Leibniz De quadratura arithmetica circuli ellipseos et hyperbolae (de aquí adelante DQA). Este escrito fue redactado por su autor a mediados de 1676, es decir, a finales del periodo que este pasó en París formándose y especializándose fundamentalmente en matemática bajo la guía de Christian Huygens, y muestra el resultado de Leibniz en el tratamiento de cuadratura de curvas. En dicho escrito, entre otras cosas, Leibniz exhibe un método riguroso de prueba para cuadraturas, presenta la cuadratura aritmética del círculo, por medio de la serie infinita de los recíprocos de los números impares alternativamente afirmados y negados (es decir, 1/1- ⅓+ ⅕ -1/7+etc.) e introduce, desde el punto de vista técnico, la utilización de cantidades infinitas e infinitamente pequeñas como ficciones útiles. En lo que respecta a la primera cuestión, en el escolio de la séptima proposición, que muestra un ejemplo de aplicación del método riguroso, cuyo núcleo fue exhibido en la proposición anterior, Leibniz introdujo una aclaración relativa a los tipos de demostraciones que pueden obtenerse en materia de cuadraturas. Como veremos, detrás de esta distinción hay reflexiones metodológicas muy importantes:
La demostración [obtenida mediante el procedimiento prescripto en la proposición anterior] tiene de singular que la cosa se agota no mediante inscriptos y circunscriptos a la vez, sino solo mediante inscriptos. Confieso, ciertamente, que no he conocido hasta ahora un camino por el que pueda demostrarse perfectamente ni una única cuadratura [1] sin una deducción al absurdo; tengo incluso razones para dudar de que esto pueda hacerse mediante la naturaleza de las cosas, sin suponer cantidades ficticias, a saber, infinitas o infinitamente pequeñas. Sin embargo, de todas las deducciones al absurdo, creo que ninguna es más simple y natural, y cercana a una demostración directa, que la que muestra no solo simplemente que entre dos cantidades no hay ninguna diferencia, y por ello que son iguales (pues, por lo demás, suele probarse mediante [2] un razonamiento doble que una no es ni mayor ni menor que otra), sino también que [3] la que emplea solamente un término medio, a saber, inscripto-circunscripto, pero no simultáneamente ambos. Y da como resultado que tengamos comprensiones más claras de estas cuestiones. (A VII 6, 537, corchetes agregados)
Como puede verse, las demostraciones se agrupan en dos grandes géneros, a saber, por un lado, las demostraciones apagógicas o por reducción al absurdo (2 y 3) y, por otro, las demostraciones directas (1). De las demostraciones por reducción reconoce dos variantes: en primer lugar, las que recurren a una doble reducción al absurdo (2), siguiendo el célebre proceso arquimediano mediante el cual se muestra que una cantidad no es mayor que una circunscripta a ella ni menor que otra inscripta; en segundo lugar, hay demostraciones por reducción que nos permiten mostrar que entre dos cantidades no hay diferencia sin tener que recurrir a un razonamiento doble, sino por medio de una única deducción al absurdo (3), o bien, como dice Leibniz, empleando un término que lo inscriba o lo circunscriba, pero no ambos a la vez. Estas demostraciones son más deseables que las anteriores, en la medida en que son más simples y, por eso, cercanas a una demostración directa. El procedimiento exhibido por Leibniz en la compleja sexta proposición de este tratado, de cuya aplicación, como dijimos antes, la séptima proposición es una muestra, exhibe un camino para obtener demostraciones apagógicas de esta naturaleza (he reconstruido esta proposición en Raffo Quintana, 20i9 64-70. Recomiendo también las reconstrucciones de Arthur 2008 20-23 y Rabouin 2015 353-358). Ahora bien, Leibniz confiesa que no ha conocido una manera de proveer demostraciones directas de cuadraturas, sin reducción al absurdo, con anterioridad a su propuesta. Más aún, pareciera que no es posible dar demostraciones de este tipo, a no ser que se supongan cantidades ficticias. Esto implica, en consecuencia, que, para dar demostraciones directas, han de suponerse tales ficciones.
Todo esto muestra al menos dos cosas: en primer lugar que, como se trata de tipos de demostraciones sobre cuadraturas, virtualmente sería posible tener, para un teorema, tres demostraciones distintas. El asunto, para Leibniz, no se reduce a una mera cuestión cuantitativa, es decir, a cuántas demostraciones pueden obtenerse. Más bien, él está interesado, por un lado, en la búsqueda de la demostración más simple, conservando, a pesar de ello, la rigurosidad de la demostración, pero permitiendo también, al mismo tiempo, ampliar el campo del descubrimiento. Así, por ejemplo, las demostraciones del tipo (3) son más simples que las (2). A pesar de que las demostraciones (2) son paradigmáticas en cuanto a la rigurosidad de la demostración, las demostraciones (3) también proveen un fundamento sólido para el "método de los indivisibles" (Leibniz se refiere nominalmente a su propio método con esta denominación, a pesar de que no emplee estrictamente hablando indivisibles (cf. Raffo Quintana, 20i8 65-66). Sobre la rigurosidad de la demostración, (cf. Rabouin 348-350; Knoblock 61-62). Ahora bien, el recurso a las cantidades ficticias, utilizadas en las demostraciones (i), permite especialmente potenciar el descubrimiento de nuevas verdades. Leibniz recurrentemente se encarga de señalar la importancia heurística que tiene el uso de cantidades ficticias, con prescindencia de la consideración acerca de si ellas existen o no en la realidad. Así, por ejemplo, señala: "Yo sin duda admitiría estos espacios y tiempos infinitamente pequeños en Geometría, a los fines de la invención, aunque fueran imaginarios" (A VI 3, 564-565). Asimismo, sostiene en DQA: "sentirán hasta dónde se extiende el campo del descubrimiento tan pronto como perciban correctamente una cosa: que toda figura curvilínea no es otra cosa que un polígono con un número infinito de lados, de magnitud infinitamente pequeña" (A VII 6, 586). Más aún, aclara que el recurso a cantidades de este tipo se asienta en un procedimiento de tipo hipotético-deductivo: "Ahora bien, es una cuestión reservada al metafísico discurrir acerca de si la naturaleza de las cosas tolera esta clase de cantidades. Al geómetra le basta demostrar qué es lo que se sigue de suponer cosas tales" (A VII 6 549).
Las cuestiones que hemos sintéticamente señalado en los párrafos anteriores sobre el procedimiento descrito por Leibniz en DQA dejan entrever que hay un gran número de interrogantes metodológicos que podrían plantearse. Por ejemplo, teniendo en cuenta los tipos de demostraciones antes señalados: ¿qué relación concibe Leibniz entre descubrimiento o hallazgo y demostración? Por lo demás, teniendo en cuenta los estándares clásicos de rigurosidad en geometría, sería esperable encontrar en DQA una organización de tipo axiomática. No obstante, nada de esto se encuentra en dicho tratado. A esto se le suma el hecho de que en 1676 Leibniz sostenía que las "primeras verdades" del conocimiento son las percepciones de apariciones, las identidades y las definiciones (A VI 3, 508-509), de manera que, en pocas palabras, el conocimiento estrictamente racional tiene lugar a partir de definiciones e identidades (algunas anticipaciones de esta concepción datan de 1672, por ejemplo, en la Accessio ad arithmeticam infinitorum, texto en el que Leibniz incluso ofrece demostraciones de los pretendidos "axiomas" a partir de definiciones; Leibniz 2014 62-69). En consecuencia, de alguna manera hay una dualidad, que genera perplejidad, entre el tipo de demostración que se apoya en definiciones e identidades y las demostraciones que Leibniz lleva a cabo en algunos textos estrictamente matemáticos. De esta manera, cabe la pregunta acerca de si en los escritos matemáticos Leibniz prescinde de una fundamentación rigurosa o bien si hay otro criterio que esté siguiendo.
Que no puedan hallarse respuestas a estas preguntas en DQA no significa necesariamente que Leibniz no tenga nada que decir al respecto. En efecto, hay reflexiones metodológicas suyas que datan del mismo periodo en que redactó DQA y que contribuyen al esclarecimiento de la problemática. En este trabajo buscaremos reconstruir la concepción metodológica de Leibniz de finales del periodo parisino y que de alguna manera subyace al abordaje del tratado leibniziano sobre cuadraturas. Esto nos permitirá mostrar, entre otras cosas, que Leibniz parece estar pensando en una concepción "heurística-demostrativa", es decir, en un procedimiento tal que permite el descubrimiento y la demostración de lo descubierto en simultáneo, y que, en las demostraciones, emplea el análisis y la síntesis con usos diversos, que describiré como "caracterizaciones" de estos procesos.
El trabajo se estructurará de este modo. En primer lugar, mostraré que Leibniz concibió el método de doble reducción al absurdo tanto para la demostración como para el descubrimiento o hallazgo, concepción que tuvo un impacto en los otros tipos de demostraciones en materia de cuadraturas que señalé anteriormente. Ahondando en la concepción leibniziana del descubrimiento, mostraré, en segundo lugar que, a lo largo del periodo parisino, Leibniz presentó diversas caracterizaciones del análisis y de la síntesis, las cuales se apoyan en distintas tradiciones históricas. Me referiré sucintamente a las concepciones de Pappus sobre el análisis y la síntesis, y a las de Zabarella acerca del método resolutivo y compositivo. En tercer lugar, buscaré dilucidar la estrategia metodológica seguida por Leibniz en DQA. Para esto, retomaré la concepción sostenida por Esquisabel, según la cual Leibniz opera con diversas perspectivas acerca del análisis y la síntesis, y mostraré la vigencia de esta clasificación en el pensamiento parisino de Leibniz. Con esto como trasfondo teórico, argumentaré que en DQA Leibniz está especialmente interesado en la obtención de nuevos resultados, motivo por el cual no es prioridad del autor proveer una organización axiomática de los conocimientos. No obstante, justificaré que esto no implica que el tratamiento de Leibniz carezca de rigor, sino que el procedimiento permite avanzar en el descubrimiento de nuevos conocimientos al mismo tiempo que queda garantizada su rigurosidad demostrativa, pues toda demostración en materia de cuadraturas es apagógica o puede convertirse en una demostración de este tipo. Más allá de esta estrategia general, tomaré algunas proposiciones para mostrar que en sus demostraciones Leibniz utiliza por momentos el análisis y por momentos la síntesis. Con esto, se pone de manifiesto que el análisis y la síntesis no constituyen métodos "cerrados", en el sentido de que se obtengan demostraciones puramente analíticas o sintéticas, sino partes de un proceso más general de demostración.
Descubrimiento y demostración
Antes señalamos que, en la época de Leibniz, las demostraciones provistas por el método de exhaución de Arquímedes eran vistas como paradigmáticas en lo que respecta a la rigurosidad de la demostración. De allí que las demostraciones propuestas por Leibniz que mencionamos antes del tipo (3) son relevantes en la medida en que, por un lado, garantizan un fundamento riguroso al método de los indivisibles, al mismo tiempo en que, por otro, son demostraciones más simples que las de doble reducción al absurdo, pues recurren a una única reducción. Ahora bien, algunos años antes de DQA, Leibniz ya había comenzado a pensar que la importancia del método de doble reducción al absurdo no se reduce a su poder demostrativo, sino que, de alguna manera, debe reconocérsele un valor heurístico:
Hasta ahora los geómetras utilizaron el método apagógico, por ejemplo, mediante [figuras] inscriptas y circunscriptas, en la medida en que solamente se propusieron demostrar cosas que fueron halladas por otros medios. He comenzado a pensar si acaso no podría ser también un principio de hallazgo: este método es tan general que comprende todas las otras cosas, puesto que todas pueden demostrarse mediante él todas las cosas halladas con otros medios. (A VII 5, 113)
Esta concepción del método de doble reducción al absurdo como un método general para la demostración y para el descubrimiento tiene implicaciones significativas. Por ejemplo, parece sugerir que los tres tipos de demostraciones en materia de cuadraturas que exhibimos anteriormente no implican métodos de demostración distintos, sino, de algún modo, casos o tipos de demostraciones que se obtienen mediante un mismo método, puesto que, a saber, de alguna manera las demostraciones del tipo (1) y (3) quedan comprendidas por (2). En este sentido, la diferencia entre ellas parece radicar más bien en cuestiones de prioridad. Así, por ejemplo, las demostraciones del primer tipo, que recurren a cantidades ficticias que compendian los procesos de pensar, hablar, descubrir y demostrar, exhiben un mayor poder heurístico (en el sentido de que "extienden el campo del descubrimiento") que las demostraciones del tipo (2), las cuales se destacan por la rigurosidad de la demostración. Estas últimas, a su vez, exhiben mayor simplicidad que las del tipo (3), en donde "simplicidad" significa, en este caso, un procedimiento más acotado de demostración: no se requiere una doble reducción al absurdo, sino una reducción simple. En este sentido podría pensarse en una especie de heurística demostrativa, esto es, en un procedimiento riguroso de descubrimiento y demostración: al descubrir, se demuestra lo descubierto. De este modo, avanzar en la búsqueda de resultados novedosos no implica que deba renunciarse a la rigurosidad demostrativa.
Ya ahondaré sobre esta noción de heurística demostrativa. Entretanto, si tenemos en cuenta que en la época de Leibniz el interés central de los matemáticos estaba puesto más en el descubrimiento de nuevas verdades que en su demostración, la idea de una heurística demostrativa parece ser especialmente atractiva. El tratado DQA parece ser una muestra de proceder de este modo, pues la ausencia de una estructura axiomático-deductiva no implica falta de rigor demostrativo; más aún, las primeras proposiciones de este texto buscan precisamente apuntalar la base demostrativa sobre la que se asienta el posterior énfasis heurístico. Por el momento, detengámonos en la idea leibniziana de descubrimiento.
El descubrimiento de nuevas verdades puede obtenerse, tanto mediante el análisis como mediante la síntesis (A VI 3, 404). En este sentido, en principio, la concepción de Leibniz no circunscribe el descubrimiento a uno de estos métodos, sea al análisis como a la síntesis. Más aún, como veremos más adelante, no hay aplicaciones "puras" de estos métodos, en el sentido de que, tanto en el descubrimiento como en la demostración, Leibniz recurre por momentos al análisis y por momentos a la síntesis. El análisis y la síntesis son, más bien, las dos partes que constituyen el arte de la invención. Ahora bien, la función que cumplen ambas partes en el descubrimiento no es clara, en el sentido de que Leibniz no siempre dice lo mismo. Si bien más adelante en el pensamiento de Leibniz el análisis tiene más importancia en la invención y la síntesis en la demostración (Esquisabel 308-309), en el periodo parisino la situación parece ser otra. En efecto, considera que la combinatoria, que es sintética, constituye el arte de inventar cuestiones o problemas, mientras que el arte de hallar las soluciones a los problemas dados por la combinatoria es el arte analítico (A VI 3, 428). De esta manera, los roles del análisis y la síntesis, usualmente más vinculados, respectivamente, a la invención y a la demostración, parecen aquí invertirse: en este esquema, la síntesis tiene preponderancia para la producción de problemas, mientras que el análisis tiene más relevancia para la demostración. No obstante, también reconoce que algunas soluciones de problemas tienen más de combinatorio que de analítico, por lo cual, en conclusión, los roles del análisis y la síntesis no tienen una demarcación clara y acabada, pues su empleo es requerido tanto para el descubrimiento como para la demostración. En este sentido, por ejemplo, en el Pacidius Philalethi Leibniz hace una descripción más bien informal del proceso de descubrimiento y demostración de verdades, que tiene connotaciones por una parte analíticas y, por otra, sintéticas:
Así como los cazadores no siguen siempre a cierta fiera designada, sino que a menudo se contentan con presas que se encuentra en el camino, así también nosotros a veces estamos obligados a agarrar las verdades que primero se nos cruzan, sin estar nunca seguros de si esta captura es beneficiosa; y cuando reunimos un número bastante grande [de verdades], habiendo extraído las razones y habiendo reconocido y dividido nuestros trabajos, entonces, finalmente, podremos tener la esperanza de hallar un tesoro mayor. (A VI 3, 538)
De alguna manera, en el arte de la invención rige una especie de principio de economía: nunca debemos trabajar en vano (cf. A VI 4, 79). Si no encontramos aquello que estábamos puntualmente buscando, es importante que al menos encontremos algo, de manera que no sea tiempo perdido. En ocasiones Leibniz incluso propone, como camino estratégico para el hallazgo de teoremas, la búsqueda de la resolución de problemas complejos: el objetivo no tiene que ser necesariamente hallar su solución, pues puede bastar con simplemente hallar algo en el intento de dar con su solución.
El análisis y la síntesis: diferentes caracterizaciones y tradiciones
Ahora bien, en este orden de ideas, no queda claro en qué consisten puntualmente el análisis y la síntesis para Leibniz. No obstante, podemos hallar caracterizaciones de estos métodos que, en principio, no son idénticas entre sí y cuya compatibilidad debe esclarecerse. Así, por ejemplo, en De imperfectione analyseos (cf. 1673), texto en el cual señala, entre otras cosas, que el descubrimiento puede obtenerse tanto por análisis como por síntesis, caracteriza estos procedimientos en función del descubrimiento de esta manera:
Sobre el análisis: "La invención tiene lugar mediante análisis, toda vez que para la invención no se asume otra cosa que el problema mismo o el teorema dado, porque la resolución en sus primeros elementos nos muestra la solución". (A VI 3, 404)
Sobre la síntesis: "La invención mediante síntesis tiene lugar cuando se requieren otros conocimientos previos [praecognita]" (A VI 3, 404). Como vemos, la diferencia entre análisis y síntesis en cuanto la invención parece estar, al menos, en la "dirección" u "orientación" de la resolución: si vamos hacia los primeros elementos, procedemos por análisis; si vamos desde conocimientos ya poseídos, avanzamos conforme a la síntesis. En esta caracterización puede decirse que el análisis "descubre lo que es primitivo, fundamental o 'simple' en la investigación de una cosa compleja", haciendo explícito lo que se encontraba implícito (Grosholz iii). Resulta claro que se trata de una caracterización matemática de estos métodos, la cual se remonta al célebre trabajo de Pappus, Mathematicae Collectiones, obra cuya importancia para la temprana modernidad es manifiesta, como atestigua no solo la traducción latina de Federico Commandino de i588 (cf. Pappus 1588), sino también, y especialmente, el empleo llevado a cabo por Descartes del análisis de Pappus aplicado a la geometría.
Pappus describe los procesos de análisis y síntesis como mutuamente dependientes: en el análisis se parte de suponer que aquello que debería obtenerse ya ha sido logrado, procediendo luego a buscar de qué cosa se sigue lo asumido, de manera que continuemos este retroceso hasta que en alguna instancia lleguemos a una proposición conocida, sea por constituir uno de los primeros principios o por estar debidamente demostrada al haber sido establecida sintéticamente (cf. Pappus i986 82-83; cf. Cellucci 97-98). En la síntesis, por su parte, se sigue el proceso contrario: si establecemos las cosas en orden natural, de manera que se disponga primero de lo precedente (los principios y proposiciones ya demostradas) y luego lo que se concluya de allí, obteniendo así el resultado buscado, por ejemplo, una demostración axiomática es un caso de razonamiento sintético.
Ahora bien, en otros textos de Leibniz, por ejemplo, en De ars inveniendi (cf. 1675), encontramos caracterizaciones de las investigaciones analíticas y sintéticas que no parecen responder a esta concepción originada en la matemática. Podríamos más bien denominarlas como filosóficológicas. Esta perspectiva parece ser más adecuada, por ejemplo, para entender el pasaje del Pacidius Philalethi citado anteriormente:
Sobre el análisis: "Una investigación es analítica cuando podemos seccionar la cosa misma en partes con gran exactitud [quanta... exactitudine]". (A VI 3, 429)
Sobre la síntesis: "[Una investigación] es sintética o combinatoria cuando asumimos algo fuera de una cosa para explicar esa cosa". (A VI 3, 429)
En este caso, el análisis enfatiza la descomposición en partes, mientras que la síntesis resalta la composición. Notemos que, en esta caracterización, síntesis y combinatoria designan lo mismo, lo que no parece que pueda decirse de la anterior. A su vez, en esta caracterización no se está pensando en un problema o un teorema (y mucho menos en tomarlo como resuelto o demostrado), sino que la referencia indeterminada a una "cosa" parece dar una imagen más amplia. En efecto, podemos concebir, así, el análisis y la síntesis de conceptos, figuras y demás "cosas" que no sean teoremas y problemas, pero que pueden resolverse y componerse. Por lo demás, como veremos a continuación, desde este punto de vista, el análisis puede tomarse en diferentes sentidos, uno de las cuales es el descrito por Leibniz en el pasaje, como descomposición en partes. Más allá de esto, vale la pena señalar que, epistemológicamente, el análisis según dicha caracterización puede implicar también el camino ascendente desde las conclusiones hasta las premisas de las que se deduce (cf. Cellucci 76). La diferencia fundamental con la caracterización anterior es que, en este caso, como no se asume demostrado el teorema (o resuelto el problema), lo que se busca es precisamente justificar la conclusión.
Podemos hallar un buen ejemplo de un abordaje lógico acerca del método en la obra de Jacopo (o Giacomo) Zabarella. Recordemos que, en la introducción de este trabajo, señalamos que Zabarella entiende que un método es un hábito lógico o intelectual cuya función es esencialmente heurística, esto es, un instrumento para hallar el conocimiento que se procura obtener. No obstante, tengamos en cuenta que Zabarella no parece haber sido directamente influyente para Leibniz en estas cuestiones. Leibniz se refiere a Zabarella pocas veces en el curso de su pensamiento juvenil e incluso, cuando lo hace, no es precisamente para referirse a cuestiones lógicas, sino más bien a temas como la "identidad diacrónica de los seres vivos" (dicho en términos de Blank 86). De cualquier modo, el influjo de Zabarella en general en el contexto de las discusiones metodológicas del siglo XVII es claro. Detengámonos sucintamente en dos aspectos del abordaje de Zabarella, que, como veremos, de alguna manera serán útiles para el esclarecimiento posterior de la concepción de Leibniz.
El primer aspecto está relacionado con la cuestión del descubrimiento y la demostración en relación con la concepción del método. En efecto, la concepción de Zabarella encierra la dualidad de otorgarle al método una función heurística, al mismo tiempo que una estructura demostrativa, en la medida en que es un hábito lógico. En cuanto a esto, Zabarella distingue dos tipos de métodos de acuerdo con su modo de proceder silogístico. En efecto, en un silogismo podemos progresar de la causa al efecto o bien del efecto a la causa. El primero de ellos es propiamente el método demostrativo, también conocido como "demostración más poderosa" o "demostración propter quid" (Zabarella 230-231). Por sus características, a este proceder de la causa al efecto se lo llama "composición". El segundo método, de los efectos a las causas, es el proceso llamado "resolución". El método resolutivo es conocido como "demostración quia" o silogismo "por el signo" o "demostración de segundo grado". Esta mera enunciación de los dos métodos nos permite advertir al menos dos cosas. En primer lugar que, aun cuando el primer método es formalmente el demostrativo, no solo nominalmente sino por la fuerza ilativa que implica, el método resolutivo también ofrece demostraciones. Esto implica, en segundo lugar, que hay dos sentidos del término demostración que están muy relacionados, pero que deben distinguirse: por una parte, el sentido amplio por el cual los dos tipos de métodos son llamados respectivamente propter quid y quia; por otra, el sentido estrecho que corresponde a las demostraciones del primer tipo por la fuerza demostrativa que tienen, precisamente por ir de las causas o -como veremos en breve-, de los principios, a los efectos o, en general, a las cosas que dependen de los principios.
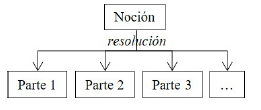
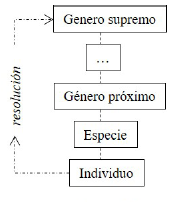
Por lo demás, obsérvese que Zabarella no recurre a las denominaciones de análisis y síntesis para referirse respectivamente al método resolutivo y al compositivo. No obstante, es usual hallar en el siglo XVII tratamientos del método en los que se denominen análisis y síntesis precisamente a los métodos resolutivos y compositivos. De este modo, puede verse, por ejemplo, al comienzo del De Corpore de Hobbes -quien, por lo demás, fue muy influyente en el pensamiento juvenil de Leibniz a propósito de diversas cuestiones-: "Y el resolutivo es comúnmente llamado método analítico, así como el compositivo es llamado sintético" (I 6, i). El segundo aspecto que vale la pena observar es el esclarecimiento de la noción de resolución que Zabarella lleva a cabo. Como hay diversas maneras de interpretar la noción de resolución, de las cuales no todas implican una estructura silogística, y dado que una formulación correcta y rigurosa del método debe implicar una estructura tal, la dilucidación de esta noción se vuelve necesaria. En este punto, su conocimiento de algunos comentadores de Aristóteles se vuelve particularmente importante, pues Zabarella detecta al menos dos sentidos de la noción de resolución, uno que fue sostenido por Amonio y el otro por Eustratio, los cuales no deben confundirse con el que él defiende (cf Zabarella 260-264). Para Amonio, el método resolutivo consiste en el desmembramiento conceptual de las partes o elementos componentes homogéneos de una cosa. Así, por ejemplo, decimos que 'hombre' se resuelve en 'cabeza', 'brazos', 'pies' y demás. En otras palabras, por resolución vamos del concepto de una cosa a los conceptos de las partes que la componen. Para Eustratio, por su parte, la resolución implica no un reconocimiento de partes homogéneas, sino el tránsito lógico desde un individuo primero a las especies, luego a los géneros próximos y así sucesivamente hasta llegar a un género supremo. Así, resolver es ir, en una categoría, desde lo particular o desde lo más específico a lo más genérico. Como puede verse, estas dos maneras de entender la resolución son muy distintas. De alguna manera, podríamos decir que, mientras que la resolución de Amonio implica un tránsito descendente desde una noción a sus partes componentes y homogéneas en cuanto al grado de especificidad (figura 1), la resolución de Eustratio implica un tránsito ascendente en una progresiva búsqueda de generalidad (figura 2).
La razón por la cual estas dos maneras de entender el método resolutivo son incorrectas es, para Zabarella, algo claro: entendida en cualquiera de estos sentidos, la resolución carece de fuerza ilativa y, sin ella, no tendríamos un método. Si no hay otro camino que nos haga ir de lo conocido a la cognición de lo desconocido sino el camino silogístico, como sostiene Zabarella, el método resolutivo de Amonio es defectuoso, dado que carece de un término medio: cuando decimos que un cuerpo se resuelve en sus partes esenciales, tenemos solamente dos términos, a saber, el cuerpo conocido y las partes desconocidas. Más aún, es claro que este proceso no describe con fidelidad el método utilizado por Aristóteles en sus tratamientos, pues, por ejemplo, el descubrimiento de que en todo cuerpo natural hay materia prima es una conclusión a la que arriba por medio del examen de los tipos de cambios. De este modo, podemos decir, en pocas palabras que, si todo cambio implica una cierta permanencia, y si la generación y la corrupción son un tipo de cambio, hay en ellos algo que permanece: lo que se conoce con el nombre de materia prima. Por lo demás, este ejemplo es útil para detectar el modo en que el método resolutivo es, de hecho, un proceso demostrativo (aunque en un sentido débil) pues, a saber, obtuvimos una demostración por los efectos. Por su parte, el método resolutivo de Eustratio también tiene el mismo defecto de carecer de fuerza ilativa, en la medida en que, de hecho, parece más bien ser una disposición ordenada que un silogismo. Por lo demás, no parece ser un camino correcto para ir de lo conocido a lo desconocido, pues en cierta medida el género supremo, así como también los diversos géneros intermedios y especies, ya deben ser conocidos antes de disponerlos ordenadamente.
Por lo demás, vale la pena señalar que para Zabarella en la matemática no tiene lugar el método resolutivo que él describe. En efecto, en la matemática la resolución implica que, después de haber llevado a cabo todas las demostraciones, retrocedemos y "resolvemos" unos teoremas en los que demostrativamente les anteceden, y así sucesivamente hasta llegar a los primeros principios. Entonces, desde el punto de vista de lo que para Zabarella es el fin del método, que es llegar a conocer lo que era desconocido, la resolución matemática es inútil, pues no da lugar a una nueva cognición. En este sentido es más bien "un ejercicio de los eruditos" más que un método resolutivo en sentido estricto, pues no nos conduce al descubrimiento de los principios que nos permitan luego demostrar otras cosas.
En síntesis, para retomar el abordaje de Leibniz, observemos que el examen de la noción de resolución llevado a cabo por Zabarella deja al descubierto que, incluso en la caracterización filosófico-lógica del análisis y la síntesis, la manera de concebir la partición o descomposición de una cosa puede ser interpretada de diversos modos. En otras palabras, la aplicación del método analítico, en la caracterización filosófica, podría implicar la resolución de un concepto en sus componentes conceptuales, la resolución de una cosa hasta el género supremo al que pertenece o el tránsito silogístico de los efectos a las causas. De este modo, en otras palabras, el simple hecho de detectar que se está llevando a cabo un análisis no alcanza para determinar qué es lo que se está haciendo.
Sobre el uso leibniziano del análisis y la síntesis en sus diversas caracterizaciones
Las caracterizaciones del análisis y la síntesis que señalamos en la sección anterior resumen las pocas clarificaciones de estos procedimientos que encontramos en el periodo parisino de Leibniz. Como vimos, no solamente podemos encontrar diversas caracterizaciones generales acerca del análisis y la síntesis, sino que también en uno de estos abordajes, el lógico-filosófico, podemos hallar interpretaciones variadas sobre el análisis. Todo esto nos presenta un panorama complejo que nos puede llevar a preguntarnos por la compatibilidad de estos procedimientos, no solamente desde el punto de vista de si las descripciones son solidarias entre sí, sino también desde el punto de vista técnico, esto es, en la aplicación que Leibniz hace del análisis y la síntesis, por ejemplo, en el tratado sobre la cuadratura aritmética. En otras palabras, podemos preguntarnos: ¿qué es lo que hace Leibniz, desde el punto de vista metodológico, en el tratado DQA? ¿Procede de acuerdo con el análisis y la síntesis en su caracterización de herencia pappusiana? ¿O bien procede de manera analítica y sintética de acuerdo con la caracterización lógica de estos términos? ¿Hay quizás otra alternativa?
Los interrogantes señalados anteriormente suponen en principio que hay una incompatibilidad entre las distintas caracterizaciones, en el sentido de que se presupone que Leibniz, desde el punto de vista metodológico, está haciendo o bien esto, o bien aquello. No obstante, no hay razones claras para defender ese supuesto. En lo que sigue esbozaré la hipótesis de que el proceder de Leibniz en DQA muestra que hay una compatibilidad entre las caracterizaciones, sobre la base de la visión de que, de hecho, Leibniz no concibe estas caracterizaciones del análisis y la síntesis como si se trataran de métodos distintos, tal que o bien se aplica uno, o bien se aplica el otro, sino que son más bien aspectos del abordaje de Leibniz que funcionan como herramientas del proceder metodológico en vistas a un objetivo particular que esté buscando en un momento determinado de su tratamiento. En otras palabras, si bien las distintas caracterizaciones del análisis y la síntesis no nos proveen métodos distintos (por ejemplo, el método analítico de la matemática, el método analítico lógico, etc.), señalan diversas funcionalidades de estos procesos. Para justificar esta hipótesis, me apoyaré en la concepción esbozada por Oscar Esquisabel, quien distingue diferentes puntos de vista acerca del análisis y la síntesis en Leibniz, cada uno de los cuales responde a un interés particular perseguido por Leibniz. De este modo, la apariencia de conflicto inicial entre las distintas aproximaciones a los procedimientos de análisis y síntesis desaparece, de acuerdo con la hipótesis de Esquisabel, una vez que se reconoce que se trata de distintas perspectivas acerca de estos procedimientos, pero no de procedimientos distintos. En este orden de ideas, la hipótesis que aquí exhibo puede interpretarse como un caso particular de esta lectura, que es reconocible no ya en los escritos metodológicos maduros de Leibniz -base sobre la que se asienta la detección de distintas perspectivas llevada a cabo por Esquisabel-, sino en los escritos matemáticos técnicos del pensamiento juvenil de Leibniz. En este sentido, luego de señalar las perspectivas detectadas por Esquisabel, quien le dará un marco teórico a esta propuesta, mi objetivo será mostrar la operatoria de estas caracterizaciones o perspectivas en algunos casos concretos, que se encuentran en el tratado DQA.
Esquisabel reconoce cuatro perspectivas acerca del análisis y la síntesis en Leibniz (311-316):
La formulación matemática, que es una caracterización que responde a la concepción de Pappus. En términos generales coincide con la primera caracterización que presentamos en la sección anterior, y que, en la época de Leibniz se asoció al álgebra gracias a Descartes y Viète.
La formulación epistémico-sintáctica, según la cual el análisis consiste en la descomposición de conceptos en nociones simples y la síntesis, en la combinatoria. El análisis implica un retorno a los principios, mientras que la síntesis, un punto de partida deductivo desde ellos. El acento está puesto aquí en la fundamentación de acuerdo con una organización axiomático-deductiva. Como vemos, en términos generales coincide con la segunda caracterización que presentamos en la sección anterior.
La formulación pragmático-epistémica que, por decirlo así, prioriza la función heurística por sobre el cumplimiento de un esquema de fundamentación axiomático-deductivo. El acento está puesto en la posibilidad de proceder a partir del conocimiento del que disponemos, no de manera axiomática, sino hipotético-deductiva, a los fines de avanzar en la solución de problemas y en la demostración de teoremas. De este modo, en la síntesis procedemos por combinación de los conocimientos previamente dados para hallar la solución de un problema, mientras que, en el análisis, buscamos de manera regresiva las condiciones para la solución de un problema, las cuales pueden sernos previamente dadas.
La formulación práctica, que ve al análisis y la síntesis en función de la relación entre medios y fines, y adquiere una perspectiva "constructiva", en el sentido práctico-productivo de la expresión. Según esta formulación, a partir de un fin propuesto, por análisis arribamos a los medios que nos conducirán a él, mientras que por síntesis procedemos a partir de conocimientos disponibles por combinación para la producción o construcción de un dispositivo nuevo.
Antes sugerimos que el modo de trabajo que puede hallarse en DQA parece priorizar lo que llamamos una heurística demostrativa, esto es, un proceder que implica avanzar en el descubrimiento de nuevas verdades con cierto orden de fundamentación, aunque este orden no sea axiomático-deductivo. En otras palabras, se prioriza una perspectiva pragmático-epistémica: hay una preponderancia estructural del tratado hacia el descubrimiento de nuevos resultados más que a la fundamentación, lo que explicaría la ausencia de una organización axiomático-deductiva, sin que esto implique la inexistencia total de fundamentación. En efecto, en ningún momento del tratado encontramos un catálogo de axiomas, bajo la modalidad de nociones comunes y postulados u otra denominación, ni de definiciones y demás. Más bien, en DQA se exhiben más de 51 proposiciones (cf. A vil 6, 520-676), de las cuales las primeras cinco son lemas (cf. A vii 6, 521), la sexta proposición es una demostración del teorema según el cual la diferencia entre dos figuras (debidamente construidas) puede hacerse menor que cualquiera dada, teorema que está en la base del procedimiento por el cual obtenemos demostraciones del tipo [3] (según la clasificación exhibida en la introducción), que es lo que encontramos en la séptima proposición. En síntesis, es claro que el acento de Leibniz en este tratado no está en ofrecer una fundamentación axiomática de los resultados que se obtengan, sino, más bien, en el hecho de hallar nuevos descubrimientos.
No obstante, esto no implica que haya una ausencia o un desinterés total por la fundamentación. El rol que tienen en el tratado las primeras siete proposiciones (en especial la sexta, que, como dijimos antes, Leibniz concibió como el fundamento riguroso del método de los indivisibles) es una muestra de esto. Precisamente por eso sostenemos que la propuesta de Leibniz es la de una heurística demostrativa, es decir, de un proceder que, si bien se orienta específicamente hacia la obtención de nuevos resultados, procura avanzar de manera rigurosa, ordenada y metódica. En consecuencia, DQA no se reduce a presentar resultados obtenidos azarosamente o faltos de fundamentación, a pesar de no contar con una organización axiomática en su exhibición. En última instancia, en este tratado el rigor demostrativo se asienta en la posibilidad de establecer demostraciones apagógicas, sea por doble reducción al absurdo o por reducción simple, pero no por una reducción hasta los axiomas. Por lo demás, no olvidemos que, al menos desde 1672, Leibniz sostuvo que, rigurosamente hablando, no hay axiomas, entendidos como verdades evidentes por sí mismas que no requieren de demostración, por lo cual aquellas proposiciones que son tenidas por axiomas también demostrarse (así por ejemplo A ii 1, 351-355; cf. Esquisabel y Raffo Quintana 2017 1324-1329). En consecuencia, de alguna manera, el modelo axiomático de demostración no parece haber sido tenido por Leibniz como el modelo de demostración rigurosa, en sentido estricto. Por el contrario, él parece haber hallado este modelo en la estructura de una demostración apagógica, tal como se exhibe en DQA. No es una cuestión menor que Leibniz haya insistido dos veces en el hecho de que en una primera lectura del tratado puede omitirse la sexta proposición, "si alguien no deseara demostrar la prop. 7 con sumo rigor" (A vi 6, 527; la otra aparición se encuentra en el index notabiliorum, A vii 6, 521), bajo pretexto de que su dificultad podría agotarnos y alejarnos de lo restante. Esto implica, en consecuencia, que las demostraciones apagógicas (Leibniz aquí se refiere explícitamente a las demostraciones simples) son, de hecho, completamente rigurosas.
En resumen, todo esto resalta que el método de Leibniz no solo -ni principalmente-demostrativo, sino heurístico demostrativo, es decir que tiene un acento especial no en la fundamentación de los conocimientos obtenidos, sino en la obtención misma de nuevos conocimientos.
Ahora bien, el modo como esta orientación general se lleva a cabo pone en juego las caracterizaciones matemática y lógico-filosófica del análisis y la síntesis. En otras palabras, visto a la luz de las perspectivas observadas por Esquisabel, en DQA se ponen en juego las primeras tres perspectivas leibnizianas sobre el análisis y la síntesis: la formulación pragmático-epistémica enmarca el programa de Leibniz para el tratado; las otras dos formulaciones, la matemática y la epistémico-sintáctica, se emplean en las demostraciones de los diversos teoremas. A continuación, examinaremos en detalle dos proposiciones claves del tratado de Leibniz, la séptima y la vigesimoprimera, como casos que atestiguan la concepción que aquí estamos esbozando. La selección de las proposiciones responde a un hecho significativo: como recién señalamos la séptima proposición es, junto con la sexta, fundamental para la obtención de las demostraciones del tercer tipo, según la clasificación que hicimos en la introducción, mientras que la proposición 21 es un caso de demostración del tipo [1], esto es, que recurre a cantidades ficticias.
Proposición 7
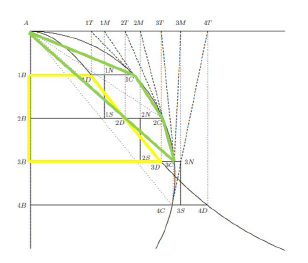
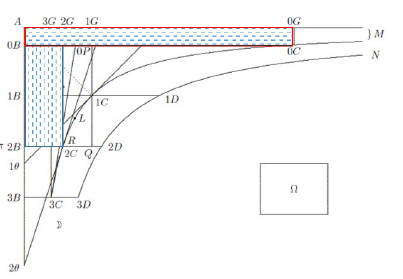
Para esta proposición debe formarse una figura peculiar (cf. A vii 6, 534). Leibniz enseña de qué manera construir, a partir de una línea curva, como A1C2C34C etc., otra curva, como A1D2D3D4D etc. (véase la figura 3). Para ello, se escogen puntos arbitrarios C en la primera curva y se establecen ordenadas, como 1B1C, 2B2C etc., y luego se trazan las tangentes a dichos puntos C, determinando, en el eje de las abscisas, los puntos T, como, por ejemplo, 1T por la tangente a 1C, 2T por la tangente a 2C y así sucesivamente. Finalmente, se trazan por los puntos T rectas perpendiculares a las ordenadas, resultando, como punto de contacto entre estas perpendiculares y las ordenadas, los puntos D. Así, por ejemplo, el punto 1D es el punto de contacto entre la ordenada 1B1C y la perpendicular a partir del punto 1T (cf. Avii 6, 535). El hecho de que se pase más bien rápido por la construcción de la figura se justifica en que ya fue introducida en la proposición anterior, la cual, como dijimos, Leibniz recomienda no tener en cuenta en una primera lectura (cf. Rabouin 358; puede verse su reconstrucción de la sexta proposición en 353-357). En cualquier caso, nuestro interés está en la demostración del teorema que emplea dicha figura, más que en la construcción misma. En efecto, el teorema señala la igualdad entre las áreas de dos espacios incluidos en la imagen, a saber, un espacio delimitado por cuatro líneas o espacio cuatrilíneo 1D1B3B3D2D1D (de ahora en más espacio Q) y un espacio delimitado por tres líneas o espacio trilíneo 1CA3C2C1C (espacio T). En el teorema acerca de las áreas de estos espacios determina que Q = 2T. Tengamos en cuenta la siguiente imagen:
Notemos que ambos espacios incluyen alguna línea curva en su conformación: Q está delimitado por tres líneas rectas y la curva 1D2D3D (visualizado en amarillo), mientras que T, por dos líneas rectas, A1C y A3C, y la curva 1C2C3C (en verde en la imagen). Desde un punto de vista metodológico, el procedimiento empleado por Leibniz aquí recurre claramente al análisis, entendido como sección de una cosa, que en este caso no es un concepto, sino una figura. La demostración de esta proposición consta de cinco artículos (cf. A vii 6, 535-536):
1. En primer lugar, se revela la estrategia de Leibniz para demostrar este teorema, que consiste en proceder por una reducción al absurdo simple, suponiendo que Q no es el doble de T, de tal modo que habría una diferencia Z, es decir, . Para esto:
Inscríbanse polígonos finitos en número a la curva C tal que el último de los polígonos de este tipo sea la figura rectilínea A1C2C3CA (llamado P).
Trácense las tangentes a los puntos C en los puntos 1M, 2M, etc.
Por las perpendiculares al eje de las abscisas a través de los puntos 1M, 2M, etc. y las perpendiculares al eje de las ordenadas a través de los puntos B, se establecen los puntos 1S, 2S, etc.
Determínese el espacio escalonado 1B1N1S2N2S3B1B (espacio 'E').
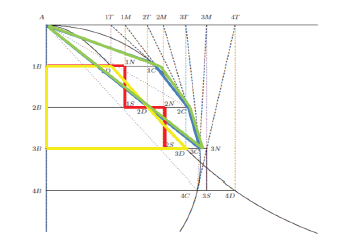
De esta manera, hemos obtenido otras dos figuras, P y E, compuestas completamente por líneas rectas. Obsérvese la figura 4, en la cual la figura P está representada en celeste y E, en rojo:
2. Leibniz avanza en la inscripción de polígonos hasta el punto de que se obtenga que la diferencia entre el polígono A1C2C3CA y el espacio trilíneo 1CA3C2C1C, por un lado, y entre el espacio rectilíneo escalonado 1B1N1S2N2S3B1B y el cuatrilíneo 1D1B3B3D2D1D, por otro, sea, en cada caso, mejor que la cuarta parte de Z (que, recordemos, es por el artículo 1 la diferencia que debería haber entre Q y 2T, supuesto que no son iguales). La posibilidad de proceder de este modo es, para Leibniz, clara: "En efecto, puede producirse hasta el punto de que se haga menor que cualquier cantidad dada" (cf. A vii 6, 536). Esta última aclaración es vital para la demostración. Ahora bien, este proceder podría parecer infundado, si no tuviéramos en cuenta que, en la sexta proposición, Leibniz argumentó que "ciertos espacios rectilíneos escalonados, así como también polígonos y demás, pueden continuarse hasta que difieran, entre ellos o bien respecto de curvas, por una cantidad menor que cualquiera dada" (A vi 6, 521). En otras palabras, la proposición sexta demuestra que la diferencia entre dos espacios (determinados según un procedimiento) puede hacerse menor que cualquier diferencia dada. Esto implica, en suma, que, en este momento de la demostración de la séptima proposición, Leibniz está procediendo por síntesis, pues, en efecto, recoge conocimientos previos.
3. En un tercer momento, Leibniz vuelve a proceder de manera sintética:
Supuestas estas cosas, es evidente, por la prop. 1, que el rectángulo 1N1B2B1S es el doble del triángulo A1C2C y el rectángulo 2N2B3B2S es el doble del triángulo A2C3C, y así para los demás, si los hubiera; por lo tanto, también la suma de los rectángulos de este tipo, es decir, el espacio escalonado será el doble de la suma de todos los triángulos de este tipo, es decir, del polígono inscripto. (A vii 6, 536)
Como vemos, Leibniz recurre a la proposición 1, que es un lema de transmutación de triángulos en rectángulos que establece que, bajos ciertas reglas de construcción, podemos determinar que un rectángulo es el doble de un triángulo (cf. A vi 3, 522-523). Ahora bien, al margen del recurso sintético a la proposición 1, en este artículo de la demostración ¡también se recurre al análisis! En efecto, Leibniz secciona el espacio escalonado E y el polígono P para establecer relaciones entre una parte de E (por ejemplo, 1N1B2B1S) y una parte de P (por ejemplo, A1C2C), sobre la base de lo cual luego generaliza y concluye, por suma de partes, que E es el doble que P.
4. Sobre la base de las cosas señaladas en los artículos y proposiciones anteriores, Leibniz extrae el último paso que necesita para concluir, en el artículo siguiente, la demostración del teorema. De esta manera, en otras palabras, el proceder en el artículo cuatro también es sintético:
En primer lugar, se recuerda que en el artículo 3 se concluyó que E es el doble de P (E = 2P).
En segundo lugar, se recuerda que en el artículo 2 se estableció, entre otras cosas, que la diferencia entre Q y E es menor que la cuarta parte de Z (|Q-E|< 1/4 Z). Dado el paso anterior, puede decirse también que |Q-2P|< 1/4 Z).
Ahora bien, en el artículo 2 también se determinó que la diferencia entre T y P es menor que la cuarta parte de Z (esto es, |P-T|< 1/4 Z). Lo mismo que se dijo recién respecto de las figuras simples, puede decirse respecto de sus dobles, esto es, |2P-2T|< 2/4 Z (aquí podría pensarse que Leibniz recurre al 'axioma' de que los equimúltiplos son como los simples; otra lectura posible es que simplemente realiza una suma).
De allí que, por la proposición 5 (esto es, por síntesis), tenemos que la diferencia entre Q y 2T es menor que tres cuartos de Z, eso es, que |Q-2T|< 3/4 Z (no nos detendremos en el detalle de la quinta proposición, que puede hallarse en A vii 6, 526-527).
5. Llegado a este punto, la contradicción es evidente: en el artículo 1 partimos de la suposición de que hay una diferencia, que llamamos Z, entre Q y el doble de T, es decir, que |Q-2T|=Z. No obstante, en el artículo 4 llegamos a que |Q-2T|< 3/4 Z, por lo que la diferencia entre Q y 2T sería al mismo tiempo Z y menos que Z, esto es, una contradicción: "Por lo tanto, no puede asumirse ninguna diferencia, pues Z puede concebirse como indefinida respeto de cualquier [diferencia], y por ello, el doble del trilíneo y el cuatrilíneo simple son iguales. Q. E. D.". (A vi 6, 536)
En conclusión, en esta proposición encontramos la demostración de un teorema en materia de cuadraturas que exhibe un resultado novedoso en su dominio. En este sentido, se observa el carácter heurístico del procedimiento de Leibniz, sin que, por ello, se pierda el rigor de la demostración, no por haber hecho descansar la proposición en axiomas de los que se deduce según una cadena silogística, sino porque el método apagógico simple cumple con los estándares de rigurosidad pretendidos. A su vez, es claro que a lo largo de este proceso de invención-descubrimiento se revelan momentos de análisis y momentos de síntesis. Quedaría por observar que la constante exigencia de construcciones que han de realizarse para la obtención de la demostración no parece entrar en conflicto con la rigurosidad de la prueba, sino que, más bien, parece ser en general un requisito para la demostración.
Proposición 21
Como señalamos antes, la proposición 21 es especialmente interesante de examinar, de acuerdo con la perspectiva que adoptamos en este trabajo, dado que Leibniz recurre a cantidades ficticias en la demostración (cf. A vii 6, 578-580). En esta proposición, en la que tenemos una curva 0C1C2C, que es un hiperboloide x n y m =a, se trata de determinar "el rectángulo 0C0GA0B, bajo la abscisa infinitamente pequeña A0B y la ordenada infinita 0B0C" (cf. A vii 6, 578). Se trata del rectángulo en rojo en la figura 5.
Ahora bien, este rectángulo puede ser [1] una cantidad infinita, si n > m; [2] una cantidad infinitamente pequeña - si n < m; o [3] una cantidad finita - si n = m. El último caso es el que aquí interesa (una reconstrucción completa de la proposición puede hallarse en Knobloch 83-84, y 1994 273-276). Leibniz dice al respecto:
Si los exponentes son iguales [es decir, si n = m] (...), consta que la curva 0C1C2C es una hipérbola cónica y que el rectángulo 0C0GA0B se iguala al cuadrado A2BR2G, según la naturaleza de la hipérbola; y no importa cuánta sea la longitud o pequeñez de las rectas A0B o 0B0C, pero el cuadrado A2BR2G es finito, y por lo tanto, el rectángulo 0 C0GA0B, comprendido bajo la [línea] infinitamente pequeña A0B y la [línea] infinitamente larga 0B0C, es finito. (A vii 6, 579)
La conclusión de Leibniz es clara: hemos obtenido que hay una igualdad entre un rectángulo delimitado por líneas infinitas e infinitamente pequeñas y un rectángulo de lados finitos, A2BR2G, que marcamos en azul en la imagen. Como vemos, la demostración es analítica. El hecho de que esta demostración se introduzca sin ulteriores precisiones puede deberse, quizás, al hecho de que la medición de espacios asintóticos era una cuestión relativamente usual en la época de Leibniz. Por ejemplo, Fermat había señalado que se pueden igualar por aproximación o "adigualar" un paralelogramo finito y un espacio asintótico en De aequationum localium transmutatione et emendatione... (ca. 1658), aunque de un modo mucho más complejo (cf. Fermat, para una reconstrucción del abordaje de Fermat y, para una profundización en la noción de adigualación, cf. Mahoney 245-254). Como vimos, por cuestiones metodológicas, Leibniz puede obtener mayor simplicidad en la demostración sin que esto implique sacrificar el rigor demostrativo.
Consideraciones finales
Para finalizar, buscaré responder los dos interrogantes que dieron lugar a este trabajo, a saber, cuál es la relación entre invención y demostración, y qué estándar de rigurosidad está contemplando Leibniz. El contexto para ambas preguntas, como vimos, es el tratado DQA. Así, con respecto a la primera cuestión, parece claro que la invención y la demostración son procesos que se involucran en la estrategia metodológica de Leibniz, en el sentido de que su intención es proveer nuevos conocimientos que estén debidamente fundados. En este sentido me referí a una heurística demostrativa. En relación con el estándar de rigurosidad tenido en cuenta por Leibniz, ante todo es claro que el interés más bien heurístico va de la mano de (y en ese sentido no se opone a) la rigurosidad. No obstante, es interesante que la rigurosidad no dependa de organizar los conocimientos de manera axiomática. En este sentido, DQA no tiene una estructura sintética, en el sentido de este término que Esquisabel describe en la formulación epistémico-sintática. El rigor es provisto más bien por la posibilidad de establecer demostraciones por reducción al absurdo, esto es, por el método de exhaución.