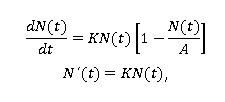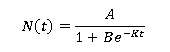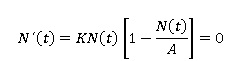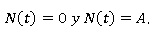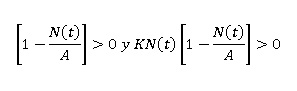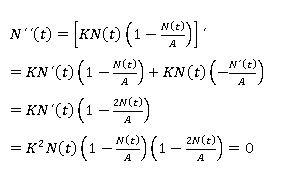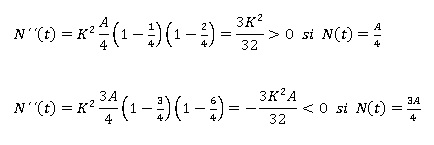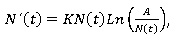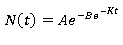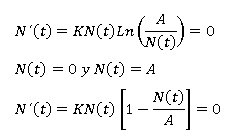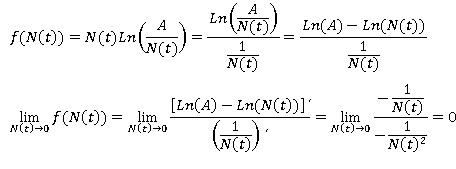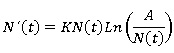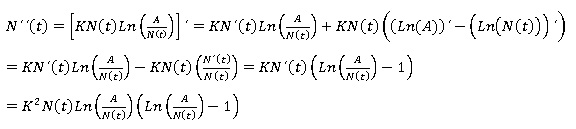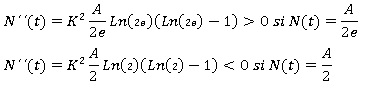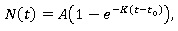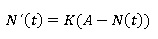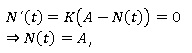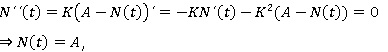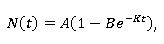INTRODUCCIÓN
El conocimiento de la dinámica de acumulación de biomasa de una especie forrajera en las diferentes épocas del año, es una metodología útil para una mejor planeación y aprovechamiento del cultivo para obtener los mayores rendimientos y material vegetal de buena calidad nutritiva (Montes et al., 2016). Para la producción de forraje se han utilizado diversas especies y variedades de hábito de crecimiento rastrero o erecto, entre ellas Brachiaria brizantha, por lo que resulta de gran interés conocer su dinámica de crecimiento en diferentes condiciones edafoclimáticas, con la finalidad de establecer mecanismos que ayuden a su mejor utilización y manejo. Los modelos matemáticos utilizados para modelar el crecimiento animal y vegetal, tienen forma sigmoidal y en ellos, pueden ser diferenciadas las siguientes fases: 1.Fase de aceleración:esta fase idealmente, debe tener su origen en el punto (0,0) y se caracteriza porque la velocidad de crecimiento es muy rápida y positiva llegando al máximo en el punto de inflexión de la curva. 2.Fase de desaceleración:a partir del punto de inflexión, la tasa de crecimiento, comienza a disminuir en virtud de una serie de factores fisiológicos que frenan el crecimiento. 3.Fase lineal:cuando el animal deja de crecer, el crecimiento puede ser considerado para la reposición de tejidos. Los modelos matemáticos aplicados al crecimiento de las plantas, permiten estimar o predecir su comportamiento temporal en diferentes condiciones (Thornley y France, 2007). Para su correcta utilización se deben tener en cuenta tres aspectos fundamentales: a) bondad de ajuste de los datos, b) capacidad de interpretación biológica, c) exigencias computacionales (Rodríguez et al., 2011; Chacín, 1998). Además, en el campo de la producción agropecuaria, (Barker et al., 2010) y (Timothy et al., 2012) plantearon que los modelos son de considerable aplicación en la descripción de procesos biológicos específicos del crecimiento y desarrollo de las plantas y en el estudio de las distintas etapas del mismo.
De esta manera, la obtención de modelos no lineales pueden ser de mucha ayuda para explicar y predecir el comportamiento de los pastos y forrajes ante de los determinados factores como la edad, estudios que son limitados en el área geográfica (Verdecia et al., 2012). Los modelos Gompertz (Laird, 1965), Logístico (Nelder, 1965), Richards (Richards, 1959), Von Bertalanffy (Bertalanffy, 1957) y Brody (Brody, 1945) son las funciones de crecimiento más frecuentemente utilizadas para describir el crecimiento de plantas, animales y organismos. Estos modelos, presentan tres parámetros con interpretación biológica y uno definido como constante matemática. El parámetro“A”, corresponde al valor asintótico. El parámetro“K”, corresponde a la tasa intrínseca de crecimiento. Así que cuanto mayor sea el valor de este parámetro más precoz es el animal o la planta y viceversa. El parámetro“B”,es denominado parámetro de integración y no posee significado biológico (Noguera et al., 2008). En general, el crecimiento de las plantas y animales es explicado por modelos como el logístico, Brody, Gompertz, Richards, entre otros (Hernández et al., 2004). En tal sentido, el conocimiento y control del crecimiento y desarrollo de los cultivos, son parámetros de gran utilidad para los investigadores, dado que su caracterización permite que los mismos puedan ser manejados eficientemente, además de posibilitar que los programas de manejo sean diseñados para las características de crecimiento inherentes a cada especie. La utilización de estos modelos puede constituir una solución al problema de estimar la producción de biomasa del pasto del king grass cuando se aplican diferentes frecuencias de corte y dosis de fertilizante nitrogenado (N), a partir de los principales factores que intervienen en su desarrollo (Rodríguez et al., 2013). Este trabajo tiene como objetivo central, en primer lugar realizar una comparación teórica con énfasis en la dinámica de crecimiento de plantas de modelos no lineales, entre ellos; Gompertz, Logístico, Von Bertalanffy y Brody, además de modelar la dinámica de producción de materia seca del pasto B. brizantha en el periodo de lluvias.
MATERIALES Y MÉTODOS
Los datos se obtuvieron de un ensayo realizado para estudiar el manejo de pastos con fertilización nitrogenada e intervalos de corte en la finca Ave María ubicada en el municipio San Genaro de Boconoito del estado Portuguesa, Venezuela, a una latitud de 8°51'53'', una longitud de -69° 50' 0'' y a una altura de 149 msnm. El material vegetal utilizado es semilla de B. brizantha con fertilización básica y aplicación en repartida en proporciones iguales, de acuerdo a la distribución de las lluvias (inicio, transición y finales), en abril-mayo, octubre y noviembre-diciembre. Los tratamientos consistieron en la edad de corte del pasto: 21, 28, 35 y 42 días y los niveles de fertilización nitrogenada: 0, 30, 60 y 120 kilogramos de nitrógeno por hectárea por año (kg N ha-1 año-1) bajo el esquema de un diseño de bloques completamente aleatorizados. La variable respuesta a considerar para la construcción del modelo es la biomasa aérea total, determinada mediante un método destructivo (cuadrícula, estufa), método peso constante. El indicador que describe a esta variable es kilogramos de materia seca por hectárea (kg MS*ha-1). La variable regresora del modelo t es días de corte. Se consideraron cuatro modelos no lineales (Gompertz (Laird, 1965), Logístico (Nelder, 1961), Von Bertalanffy (Bertalanffy, 1957) y Brody (Brody, 1945)) para estudiar la relación entre la edad de corte y la fertilización nitrogenada con los rendimientos. Los análisis estadísticos se realizaron en el entorno de programación R. Así mismo, se realizó una descripción teórica de los modelos no lineales mencionados como se presenta a continuación, esto con el fin de caracterizarlos y permitir compararlos en términos de su potencial uso en el modelado de la dinámica del crecimiento de especies forrajeras.
Modelo Logístico. En el modelo de crecimiento logístico se explica que a mayor población, menor tasa de crecimiento (Nelder, 1961).
A continuación se presenta la ecuación diferencial del modelo logístico:
Donde A es una constante positiva que se refiere al crecimiento máximo de la población.
En esta constante aparecen resumidas un buen número de circunstancias, que influyen de manera decisiva en el desarrollo de la población, a saber: factores climatológicos, disponibilidad de nutrientes, recursos del medio, entre otros. La tasa de crecimiento K deja de ser constante para pasar a autorregularse según el tamaño de la población en cada instante (Bello, 2014).
La solución explícita de la ecuación diferencial anterior está dada por la siguiente expresión conocida como modelo logístico:
Donde B es cualquier número real positivo que depende de la condición inicial N (0).
A es el valor del crecimiento máximo de la población.
K es la tasa intrínseca de crecimiento.
Puntos de equilibrio: En este caso se trata de encontrar todas las soluciones cuya derivada es igual a cero. Por lo tanto se tiene que:
Entonces, los dos únicos puntos de equilibrio de la ecuación logística son:
Estudio del crecimiento de las soluciones. Los dos puntos de equilibrio dividen el plano en tres regiones: R1 valores de N(t) por encima de A, en cuyo caso se dice que la situación es de sobrepoblación, R2 para tamaños poblacionales N(t) entre 0 y A, que es el caso biológico estándar y R3 para tamaños poblacionales N(t) < 0, donde la ecuación carece de sentido biológico (Bello, 2014).
En el interior de R2 la derivada no puede cambiar de signo, dado que 0 < N(t) < A, entonces se tiene que:
De ahí que N(t) ha de ser creciente en R2.
Estudio de la concavidad de las soluciones: La información la proporciona en este caso la derivada de segundo orden de N(t) (Bello, 2014). Para la ecuación logística se obtiene la siguiente expresión:
En ese orden, Bello (2014) señala que en este caso, la expresión anterior se anula únicamente cuando N(t) = 0, N(t) =A, o bien N(t) = A/2. De allí que, las dos primeras opciones no conducen a candidatos a puntos de inflexión, pues no son más que los puntos de equilibrio del modelo. Por lo tanto, de existir algún punto de inflexión, éste habría de ser N(t) = A/2. Por otra parte, para estudiar el signo de N´´(t) en R2 y poder concluir de ese modo, sí N(t) = A/2 es o no un punto de inflexión. Basta con elegir un punto cualquiera entre 0 y A/2, por ejemplo, N(t) = A/4, otro entre A/2 y A por ejemplo, N(t) = 3A/4, evaluar N´´(t) en ambos puntos y verificar sí se produce o no un cambio de signo. En caso de producirse, se podría asegurar que en A/2 hay en efecto un punto de inflexión y se tiene que:
Luego en el nivel N(t) = A/2 la solución pasa de ser convexa (N´´(t) > 0) a ser cóncava (N´´(t) < 0), por lo que A/2 es un punto de inflexión. Finalmente la imagen de
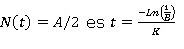 lo que permitiría determinar la edad del pasto al punto de inflexión.
lo que permitiría determinar la edad del pasto al punto de inflexión.
Modelo Gompertz. Este modelo asume que la tasa de crecimiento se incrementa de manera monótona hasta cuando alcanza un máximo y después decrece en forma monótona asintóticamente. La correspondiente curva de crecimiento es una sigmoidal, con un punto de inflexión y una asíntota (Lawrence y Flower, 2002).
A continuación se presenta la ecuación diferencial de Gompertz (Laird, 1965).
Donde:
K: Tasa intrínseca de crecimiento
A: Valor máximo de crecimiento.
La ecuación diferencial de Gompertz puede resolverse explícitamente y sus soluciones son:
Donde:
B: es un número real positivo que desplaza el modelo a la izquierda o a la derecha.
e=número irracional (base del logaritmo neperiano), A=es el valor máximo de crecimiento t=el tiempo, k=establece la tasa intrínseca de crecimiento. Esta ecuación es conocida como la ecuación de Gompertz.
Puntos de equilibrio: Para obtener los puntos de equilibrio de la ecuación Gompertz, basta con resolver la siguiente ecuación diferencial:
Procediendo con ligereza, se podría afirmar que los dos únicos putos de equilibrio de la ecuación de Gompertz son N(t) = 0 y N(t) = A. Sin embargo, para poder afirmar que N(t) = 0 lo es, se hace imprescindible un análisis algo más sutil. La razón estriba en el hecho de que la función
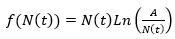 no está bien definida en N(t) = 0, pues genera una indeterminación del tipo
no está bien definida en N(t) = 0, pues genera una indeterminación del tipo
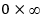 (Bello, 2014).
(Bello, 2014).
Para deshacer dicha indeterminación se dispone de la llamada regla de L´Hopital (Steward y Romo, 2008), según la cual f (N (t) ) que también puede escribirse como un cociente de la siguiente forma:
En consecuencia, la cantidad f (0) que a priori parecía una indeterminación resulta no ser más que un objeto matemático ya que en cero se comporta igual que lo hace N (t), es decir, f (0) = 0.
Estudio del crecimiento de las soluciones. Como en el caso de la ecuación logística, los dos puntos de equilibrio (N (t) = 0 y N (t) = A) dividen el plano en tres regiones:
R1 (valores de N (t) por encima de A), R2 (valores de 0 < N (t) < A) y R3 (para valores negativos de N (t) que carecen de significado biológico). Haciendo un análisis de la ecuación diferencial de Gompertz dada a continuación:
Se sabe que en el interior de cada una de estas regiones, la derivada no puede cambiar de signo. Para conocer el signo de N (t)´ en R1, basta con evaluar el segundo miembro en un punto cualquiera que sea mayor que A, por ejemplo, N (t) = 2A , de donde se obtiene que
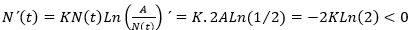 , luego N (t) ha de ser decreciente en R1, lo que concuerda con lo que la intuición biológica dicta en el régimen de sobrepoblación (Bello, 2014). Si se elige ahora un punto arbitrario de R2, por ejemplo N (t) = A/2, resulta que
, luego N (t) ha de ser decreciente en R1, lo que concuerda con lo que la intuición biológica dicta en el régimen de sobrepoblación (Bello, 2014). Si se elige ahora un punto arbitrario de R2, por ejemplo N (t) = A/2, resulta que
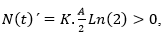 , luego N (t) , ha de ser creciente en R2.
, luego N (t) , ha de ser creciente en R2.
Por último, si se pretendiera repetir este cálculo en R3 usando por ejemplo, el valor N (t) = -A, se llegaría a la situación absurda de tener que evaluar el logaritmo neperiano en una cantidad negativa, lo que carece de sentido.
Estudio de la concavidad de las soluciones. Para conocer la concavidad del modelo Gompertz se hace uso del criterio de la segunda derivada de N (t) (Steward y Romo, 2008):
Que únicamente se anula cuando N (t) = 0, N (t) = A o bien N (t) = A/e.
Las dos primeras opciones, no conducen a candidatos a nivel de inflexión, pues no son más que los puntos de equilibrio del modelo, por tanto, de existir algún nivel de inflexión éste habría de ser N (t) = A/e.
Para estudiar el signo de N´´ (t) en R2 y poder concluir de ese modo si N (t) = A/e es o no un nivel de inflexión, basta con elegir un punto cualquiera entre 0 y A/e por ejemplo, N (t) = A/(2e), otro entre A/e y A, por ejemplo, N (t) = A/2, evaluar N´´ (t) en ambos puntos y verificar si se produce o no un cambio de signo. En caso de producirse, podría asegurarse que en A/e hay en efecto un nivel de inflexión (Bello, 2014).
Se tiene que:
Luego en el nivel N (t) = A/e la solución pasa de ser cóncava ( N ´´(t) > 0 ) a ser convexa hacia abajo N ´´(t) < 0, por lo que A/e es un auténtico nivel de inflexión. Así mismo, en lo que concierne a la estabilidad de los puntos de equilibrio, es inmediato concluir que N (t) = 0 es claramente inestable, mientras que N (t) = A es asintóticamente estable.
Finalmente la imagen de
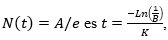 lo que permitiría determinar la edad del pasto al punto de inflexión.
lo que permitiría determinar la edad del pasto al punto de inflexión.
Modelo de von Bertalanffy. Según Bello (2014) el crecimiento individual de muchos organismos, ya sea longitudinal o en peso, como la longitud de un pez, crustáceo o molusco, se esbozan gráficamente en función de la edad y en la mayoría de los casos se obtiene una curva cuya pendiente disminuye continuamente después de cierta edad, aproximándose a una asíntota máxima. Una ecuación que se ajusta a este comportamiento es la propuesta de von Bertalanffy (Bertalanffy, 1957), cuya ecuación es:
Donde:
N (t) es la longitud del individuo al tiempo t,
A es la longitud máxima del individuo (asíntota máxima),
K es el parámetro de curvatura que expresa qué tan rápido la longitud alcanza su valor máximo.
t es el tiempo.
t 0 , es el valor teórico del tiempo en el cual la longitud es cero.
Este modelo tiene como suposiciones básicas, las siguientes:
1.- El organismo crece isométricamente.
2.- La tasa de crecimiento de un individuo no está influenciada por el tamaño poblacional.
Ecuación diferencial de von Bertalanffy:
Puntos de equilibrio:
Por lo tanto, el único punto de equilibrio de la ecuación de Bertalanffy es N (t) = A.
Estudio del crecimiento de las soluciones. En este caso, el punto de equilibrio de la ecuación de Bertalanffy divide el plano en dos regiones:
R1 (valores de N (t) > A), en cuyo caso se dice que la situación es de valores de longitud mayores al máximo y R2 (valores de 0 < N (t) < A), que es el caso biológico estándar. En la región R1 la derivada no puede cambiar de signo, ya que si entonces se tiene que k (A - N (t)) < 0, lo que implica que N (t) es decreciente en R1. En el interior de la región R2 la derivada no puede cambiar de signo, ya que si 0 < N (t) < A entonces se tiene que k (A - N (t)) > 0, lo que implica que N (t) es creciente en R2.
Estudio de la concavidad de las soluciones. La segunda derivada de N (t).
Que únicamente se anula cuando N (t) = A, este valor no es candidato a punto de inflexión, dado que no es más que un punto de equilibrio del modelo, por tanto no existe punto de inflexión.
Para estudiar el signo de N´´ (t) en R2 y poder concluir acerca de la concavidad de N (t), se toma un valor por ejemplo N (t) = A/2, entonces:
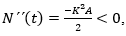 por lo tanto la función N (t) es cóncava.
por lo tanto la función N (t) es cóncava.
Modelo de Brody. Como caso particular del modelo de von Bertalanffy. Según Bello (2014), la ecuación diferencial de Brody (Brody, 1945) considera que la velocidad de crecimiento en peso es proporcional al crecimiento que falta para llegar al peso máximo, se tiene:
N´(t) = K(A - N(t)), e integrando se obtiene el modelo de Brody:
Donde: N(t) representa el peso del animal al tiempo t , A representa el tiempo máximo cuando t tiende al infinito, B es un parámetro de ajuste cuando t = 0 y representa una proporción del peso máximo y K es el índice de madurez que da la rapidez de crecimiento, hacia el valor del peso máximo. Esto significa que cuanto más grande sea el valor de K, éste representa un crecimiento explosivo y entre más pequeño sea, el crecimiento es retardado.
RESULTADOS Y DISCUSIÓN
En las Tablas 1 y 2 se presentan los resultados del ajuste de dos modelos no lineales a datos de materia seca acumulada (Kg MS ha-1) en pastos B. brizantha a diferentes edades de corte y bajo fertilización nitrogenada en época de lluvias. Se observa como ambos modelos muestran un excelente ajuste al conjunto de datos de materia seca acumulada con un R2 = 1.0 para los modelos logístico y Gompertz. No obstante, el modelo Gompertz muestra un menor valor de AIC (507,37) así como un menor error estándar residual (306,1) en comparación con los valores obtenidos mediante el modelo logístico correspondientes a un AIC = 537,0498 y un error estándar residual de 496,3. Los resultados antes señalados sugieren que en el periodo lluvioso (Tabla 2) el modelo de mejor ajuste para estimar la producción de materia seca acumulada (Kg MS ha-1) en B. brizantha a diferentes edades de corte y bajo fertilización nitrogenada es el Gompertz. Estos resultados coinciden con lo señalado por Rodríguez et al. (2011) en un ensayo para estimar la dinámica de crecimiento de Pennisetum purpureum vc. Cuba CT-169, quienes reportan que los modelos clásicos de crecimiento, Gompertz para el período lluvioso y logístico para el poco lluvioso, son los de mejor ajuste para las variables acumulación de materia seca y altura de la planta. Así mismo, Martínez et al. (2010), Rodríguez et al. (2011) y Rodríguez et al. (2013) en la modelación del rendimiento de MS acumulada de King grass o de sus clones, concluyeron que los modelos Gompertz y logístico fueron los de mejor ajuste. En estos trabajos se consideran funciones que permiten estimar la producción de biomasa en función del tiempo.
Tabla 1 Ajuste de un modelo logístico para estimar la producción de materia seca acumulada (Kg MS ha -1 ) en Brachiaria brizantha a diferentes edades de corte (días) y bajo fertilización nitrogenada (Kg N ha -1 ) en época de lluvias.
| Tratamiento | Edad al punto de inflexión (t) (días) | Autocorrelación | Ajuste del modelo | Parámetros estimados del modelo y su significancia | Error estándar residual | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dosis de N (Kg N*ha -1 ) | Edad de corte (días) | dw | P valor | R 2 | AIC | A | P valor | B | P valor | K | P valor | |||
| 0 | 21 | 144 | 0,1583 | 0,0000 | 0,9989 | 678,155 | 14310 | 0,0000 | 25,7600 | 0,0000 | 0,0226 | 0,0000 | 156,7 | |
| 0 | 28 | 128 | 1,0613 | 0,0007 | 0,9884 | 593,089 | 23420 | 0,0000 | 23,0600 | 0,0000 | 0,0244 | 0,0000 | 854,7 | |
| 0 | 35 | 130 | 0,3641 | 0,0000 | 0,9959 | 442,342 | 27030 | 0,0000 | 27,7600 | 0,0000 | 0,0256 | 0,0000 | 598,1 | |
| 0 | 42 | 143 | 0,2316 | 0,0000 | 0,9968 | 451,714 | 38000 | 0,0000 | 18,2500 | 0,0000 | 0,0203 | 0,0000 | 707,1 | |
| 30 | 21 | 155 | 0,1875 | 0,0000 | 0,9988 | 698,668 | 17730 | 0,0000 | 23,1800 | 0,0000 | 0,0202 | 0,0000 | 190,9 | |
| 30 | 28 | 141 | 0,4485 | 0,0000 | 0,9965 | 553,964 | 25870 | 0,0000 | 25,0200 | 0,0000 | 0,0229 | 0,0000 | 496,4 | |
| 30 | 35 | 128 | 0,3302 | 0,0000 | 0,9962 | 448,891 | 31640 | 0,0000 | 26,7500 | 0,0000 | 0,0256 | 0,0000 | 672,3 | |
| 30 | 42 | 138 | 0,2355 | 0,0000 | 0,9970 | 459,261 | 44470 | 0,0000 | 17,5600 | 0,0000 | 0,0208 | 0,0000 | 809,1 | |
| 60 | 21 | 166 | 0,0848 | 0,0000 | 0,9985 | 709,879 | 18940 | 0,0000 | 2,3610 | 0,0298 | 0,0270 | 0,0043 | 287,1 | |
| 60 | 28 | 142 | 0,1634 | 0,0000 | 0,9969 | 549,938 | 26140 | 0,0000 | 23,5200 | 0,0000 | 0,0222 | 0,0000 | 469,4 | |
| 60 | 35 | 119 | 0,2557 | 0,0000 | 0,9950 | 457,846 | 31590 | 0,0000 | 27,0700 | 0,0000 | 0,0186 | 0,0000 | 212,6 | |
| 60 | 42 | 140 | 0,2415 | 0,0000 | 0,9971 | 464,084 | 50780 | 0,0000 | 16,3000 | 0,0000 | 0,0200 | 0,0000 | 881,9 | |
| 120 | 21 | 123 | 0,1087 | 0,0000 | 0,9979 | 683,400 | 10560 | 0,0000 | 21,5600 | 0,0000 | 0,0005 | 0,0000 | 164,8 | |
| 120 | 28 | 142 | 0,4718 | 0,0000 | 0,9972 | 534,746 | 21810 | 0,0000 | 28,4600 | 0,0000 | 0,0236 | 0,0000 | 380,1 | |
| 120 | 35 | 128 | 0,3580 | 0,0000 | 0,9975 | 417,876 | 22150 | 0,0000 | 31,4600 | 0,0000 | 0,0270 | 0,0000 | 386,4 | |
| 120 | 42 | 142 | 0,2196 | 0,0000 | 0,9969 | 448,944 | 34560 | 0,0000 | 25,2500 | 0,0000 | 0,0227 | 0,0000 | 673,0 | |
| Promedio | 0,3075 | 0,0000 | 0,9966 | 537,0498 | 27438 | 0,0000 | 22,7076 | 0,0019 | 0,0215 | 0,0003 | 496,3 | |||
Tabla 2 Ajuste de un modelo Gompertz para estimar la producción de materia seca acumulada (Kg MS ha -1 ) en pastos Brachiaria brizantha a diferentes edades de corte (días) y bajo fertilización nitrogenada (Kg N ha -1 ) en época de lluvias.
| Tratamiento | Edad al punto de inflexión (t) (días) | Autocorrelación | Ajuste del modelo | Parámetros estimados del modelo y su significación | Error estándar residual | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dosis de N (Kg N*ha -1 ) | Edad de corte (días) | dw | P valor | R 2 | AIC | A | P valor | B | P valor | K | P valor | |||
| 0 | 21 | 127 | 0,158 | 0,000 | 0,9980 | 708,281 | 16420 | 0,000 | 4,666 | 0,000 | 0,012 | 0,000 | 209,4 | |
| 0 | 28 | 110 | 1,061 | 0,001 | 0,9927 | 576,338 | 26110 | 0,000 | 4,656 | 0,000 | 0,014 | 0,000 | 677,3 | |
| 0 | 35 | 112 | 0,364 | 0,000 | 0,9985 | 413,662 | 30140 | 0,000 | 5,094 | 0,000 | 0,015 | 0,000 | 358,4 | |
| 0 | 42 | 120 | 0,232 | 0,000 | 0,9983 | 433,316 | 41710 | 0,000 | 4,181 | 0,000 | 0,012 | 0,000 | 509,1 | |
| 30 | 21 | 142 | 0,188 | 0,000 | 0,9990 | 691,672 | 21500 | 0,000 | 4,304 | 0,000 | 0,010 | 0,000 | 178,5 | |
| 30 | 28 | 126 | 0,449 | 0,000 | 0,9995 | 483,974 | 30210 | 0,000 | 4,635 | 0,000 | 0,012 | 0,000 | 178,5 | |
| 30 | 35 | 110 | 0,330 | 0,000 | 0,9990 | 410,636 | 35150 | 0,000 | 5,029 | 0,000 | 0,015 | 0,000 | 339,6 | |
| 30 | 42 | 114 | 0,236 | 0,000 | 0,9994 | 412,444 | 48260 | 0,000 | 4,166 | 0,000 | 0,013 | 0,000 | 350,7 | |
| 60 | 21 | 160 | 0,085 | 0,000 | 0,9982 | 720,007 | 24500 | 0,000 | 4,078 | 0,000 | 0,009 | 0,000 | 234,4 | |
| 60 | 28 | 128 | 0,163 | 0,000 | 0,9994 | 489,678 | 30840 | 0,000 | 4,460 | 0,000 | 0,012 | 0,000 | 203,3 | |
| 60 | 35 | 101 | 0,256 | 0,000 | 0,9994 | 397,421 | 34150 | 0,000 | 5,315 | 0,000 | 0,017 | 0,000 | 268,2 | |
| 60 | 42 | 116 | 0,242 | 0,000 | 0,9996 | 410,280 | 55490 | 0,000 | 3,973 | 0,000 | 0,012 | 0,000 | 337,4 | |
| 120 | 21 | 103 | 0,109 | 0,000 | 0,9987 | 657,762 | 11430 | 0,000 | 4,552 | 0,000 | 0,015 | 0,000 | 128,8 | |
| 120 | 28 | 127 | 0,472 | 0,000 | 0,9993 | 484,888 | 25490 | 0,000 | 4,916 | 0,000 | 0,013 | 0,000 | 190,2 | |
| 120 | 35 | 110 | 0,358 | 0,000 | 0,9986 | 402,273 | 24460 | 0,000 | 5,483 | 0,000 | 0,015 | 0,000 | 292,5 | |
| 120 | 42 | 120 | 0,220 | 0,000 | 0,9987 | 425,295 | 37420 | 0,000 | 5,045 | 0,000 | 0,014 | 0,000 | 441,2 | |
| Promedio | 0,308 | 0,000 | 0,9985 | 507,370 | 30830 | 0,000 | 4,660 | 0,000 | 0,013 | 0,000 | 306,1 | |||
Por otro lado, en la Tabla 2 se observa que el mayor valor de la ordenada t del punto de inflexión (160 días), se obtiene para una dosis de nitrógeno (60 Kg N ha-1) y una edad de corte del pasto de 21 días. Esto sugiere, que bajo ésta condición experimental la producción de materia seca acumulada de B. Brizantha se mantiene de manera sostenida por un período de tiempo mayor que el resto de las condiciones experimentales en este ensayo. En ese sentido, determinar los momentos óptimos de corte o cosecha, con base a los valores obtenidos en las dinámicas de crecimiento de la especie en un lugar y clima en particular, permite maximizar el rendimiento de forraje, mayor obtención del componente hoja en lugar de tallos y material muerto, obteniéndose forraje de mayor calidad nutritiva en comparación a los cortes que se hacen cuando el forraje ya está seco (Castro et al., 2017).
Por tanto, este resultado sugiere que la fertilización nitrogenada, la edad de corte, la tasa intrínseca de crecimiento del pasto B. brizantha, así como los demás factores que afectan el desarrollo de esta especie forrajera determinan la sustentabilidad en la producción de materia seca de esta especie, lo que coincide con lo señalado por (Bello, 2014) en una descripción teórica de los modelos no lineales, especialmente del modelo Gompertz y logístico en relación con los factores que afectan la ordenada X del punto de inflexión. Mas aún, las dinámicas de crecimiento, determinan el comportamiento fenológico del cultivo en las diferentes épocas del año, el cual varía dependiendo de las condiciones ambientales que se presenten (Montes et al., 2016), por lo que el crecimiento y calidad de los pastos puede variar considerablemente de acuerdo con el manejo a que se someten, con efectos favorables o no según la especie de planta y las condiciones edafoclimáticas (Del Pozo, 1998). Esto coincide con lo reportado por Cruz et al. (2017), quienes en un ensayo con pasto mulato a diferente frecuencia e intensidad de pastoreo, concluyeron que durante la época de lluvias el pasto presenta mayor acumulación de forraje al cosecharse en periodos de 28 días con pastoreos ligeros.
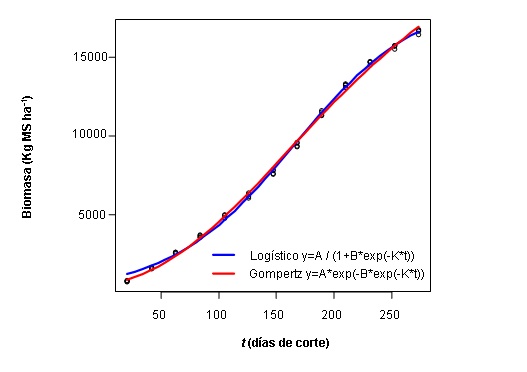
En la Figura 1, se muestran las estimaciones de la producción de materia seca acumulada en pasto B. brizantha a una edad de corte de 21 días y bajo fertilización nitrogenada (0 Kg N ha-1) en época de lluvias, según los modelos logístico y Gompertz. En relación al parámetro A (asíntota máxima de producción de materia seca), se verificó que para esta condición experimental el modelo Gompertz proporcionó estimaciones más próximas a la producción máxima de materia seca acumulada (16420 Kg MS ha-1) que el modelo logístico y que el resto de los tratamientos ensayados. El parámetro B es el factor de integración que ajusta los valores de producción inicial de materia seca. En ese sentido, los dos modelos tendieron a subestimar la producción inicial de materia seca de esta especie de pasto. La velocidad de crecimiento para alcanzar el desarrollo pleno del cultivo (K) es indicativo de un desarrollo precoz, pues cuanto mayor es el valor de K, más rápidamente el pasto alcanza su desarrollo. Es importante señalar que el ensayo se llevó a cabo en la época de lluvia, lo que sugiere crecimiento acelerado del pasto, ya que esta especie concentra la mayor parte de la producción de materia seca durante el período de lluvias (Merlo et al., 2017). Sin embargo, al confrontar los valores de K con ambos modelos, se observa que el modelo Gompertz muestra una mayor velocidad de crecimiento (0,012) comparado con el logístico (0,0226).
CONCLUSIONES
Los puntos de equilibrio de los cuatro modelos no lineales considerados en esta investigación están relacionados directamente con el crecimiento máximo de la población, reflejado en la constante A. El punto de inflexión en el modelo Logístico y el Gompertz están condicionados por la tasa intrínseca de crecimiento, por la producción inicial de materia seca y por los factores que afectan el crecimiento del pasto. Los modelos Von Bertalanffy y Brody carecen de un punto de inflexión. En el periodo lluvioso el modelo de mejor ajuste para estimar la producción de materia seca acumulada en pastos B. brizantha a diferentes edades de corte y bajo fertilización nitrogenada fue el Gompertz. Los dos modelos tendieron a subestimar la producción inicial de materia seca. El modelo Gompertz presentó una mayor velocidad de crecimiento que el logístico.